应变式结构断面错动测试装置开发与应用

范 亮，李鸿岩，郭思均

应变式结构断面错动测试装置开发与应用

范 亮1，李鸿岩1，郭思均2

（1. 重庆交通大学 土木工程学院，重庆 400041；2. 云南建设投资控股集团有限公司，云南 昆明 650000）

为了精确测量结构断面错动微量值、解决传统测量方法存在的问题，自主设计了一套结构断面错动测试装置。该装置由弹簧片形成的小梁、固定端、应变测量系统等组成。通过改变小梁的长度和厚度控制测量装置的分辨率和工作范围；通过改变应变测量系统的桥路组合以满足测量方向的要求。该装置可以直接测量近距离两点间的错动量，可以进行单向测量和双向动态测量。该装置适用性强，测量精度为±0.002 mm，具有较强的应用价值。

组合结构；错动微量；弹簧片

组合结构、叠合结构及拼装结构等由于材质、构造、工艺等因素，结构表面留有接缝或断面接触面，而这些接缝或断面在荷载作用下会产生一定的微量滑移，产生的滑移对结构的刚度和强度有较大的影响[1]，因此精准地测量滑移量就显得尤为重要。国内外在进行钢-混凝土组合结构[2-7]、梁柱节点变形[8-11]和弦支穹顶索撑节点滑移[12]等的测量中，均将断面间的滑移值测量作为实测主要参量之一。然而迄今为止，测量断面滑移的方式主要是利用各类百分表或千分表进行，而且百分表或千分表在测量时需要进行改装设计，自身的体积决定了其无法测量极近距离两点的位移量[13]（即断面滑移量）。

1 测试装置工作原理

如图1所示，将弹簧片制成的小梁跨过错动界面，一端固定，另一端随相对错动点移动，断面错动量转化为小梁的梁端位移。对于有确定边界、材料及尺寸的小梁，其梁端位移与任意截面的应变间有明确的力学关系，通过该关系，将梁端位移与截面应变相关联。因此，通过量测截面应变，可以得到断面错动量值，一般情况下，该应变与错动量值间的关系为线性关系。

图1 错动量与梁端位移关系原理图

1.1 断面错动量与梁端位移的关系

1.2 梁端位移与截面应变的关系

图2中，①为弹簧片制成的小梁；②为梁的挠曲线；③为应变测量位置；④为小梁的横截面形式。

图2 梁端位移与截面应变关系原理图

将弹簧片形成的小梁一端固定、一端施加一个强制位移，且对应的外力为，测得受弯区段任一点的纵向线应变，代入小梁的弯矩方程确定其方程的系数，进而求出小梁的挠度方程，用求出的挠度方程即可计算施加的位移。

从材料力学可知，弹簧片形成的小梁任意横截面上任一点处的纵向线应变表达式为

中性轴曲率半径有如下关系：

将（2）代入（1）得应变计算公式为

在=位置截面的应变为

外力的表达式为

从材料力学可知，小梁的挠曲线方程为

当=时，小梁B端的位移为

因此，得到梁端位移与任意截面纵向线应变的关系为

断面错动量与任意截面线应变的关系为

2 测试装置设计

2.1 装置构造

由图3可知，该测量装置由固定端Ⅰ、固定端Ⅱ、应变片和小梁组成。小梁的一端固定于固定端Ⅱ，固定端Ⅱ固定在断面Ⅰ的表面，固定端Ⅰ固定在断面Ⅱ的表面；小梁上设置有钢珠和应变片；钢珠设置在离固定端Ⅱ近边距离为的位置，提供位移施加点；应变片设置在离固定端Ⅱ近边距离为的位置，用于测量截面应变值；当断面Ⅰ和断面Ⅱ的接触面发生错动时，钢珠位置处产生位移，通过应变片处测量的截面应变值计算出断面错动位移。

图3 装置构造平面图

2.2 适用说明

通过（8）式推出分辨率及最大量程的表达式分别为式（9）和式（10）。量程范围内小梁的变形段在其线弹性范围内。

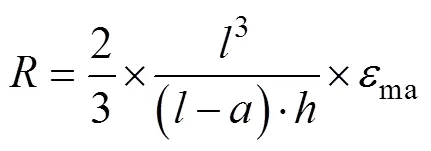
从式（9）和式（10）可以看出，装置的分辨率与小梁的长度和厚度有关系，小梁的长度越大，装置的测量分辨率就越低，量程就越大。反之，小梁长度越小，装置的测量分辨率就越高，量程就越小。因此，为了准确测量，应根据实际情况合理设计小梁的长度和厚度。

根据实际的需要该装置可以制作成单向测量装置（将图3中固定端Ⅰ去掉一半即可）；也可做成双向测量装置（图3所示）。双向测量装置可以用于反复循坏错动的疲劳测量。

3 装置实际测试结果与分析

该装置的工作原理表明，界面错动量与小梁应变为线性关系。以下将对该装置进行标定，同时验证其测试精度及稳定性。

采用的装置尺寸及材料为：

固定端Ⅰ：5 mm×5 mm×5 mm方磁铁；

固定端Ⅱ：10 mm×10 mm×5 mm方磁铁；

小梁：=1.5 cm、=0.3 mm的钢片；

应变片：3 mm电阻应变片，位置0.75 cm。

在实际制作中，由于操作误差，小梁的长度和应变片的位置不可能控制得很好，只能无限地接近，所以每一个装置分辨率的计算值和真实值存在一定的误差，该测量装置的精度需要通过标定的数据确定。

图4为量测装置的标定示意图。具体标定过程如下：

图4 装置标定图

（1）待标定装置为单向量测装置，将量测装置与千分表固定于标定台之上，使千分表的中心对准小梁上的位移施加点，且小梁与千分表的中心线垂直；

（2）将小梁上的应变片以1/4桥路形式连接应变仪；

（3）打开应变仪与相应的软件进行调试；

（4）将千分表与小梁紧密接触，对应变仪进行平衡清零；

（5）给小梁逐级施加位移并采集应变数据，每一级为0.1 mm，施加到0.5 mm时停止加载；

（6）记录数据；

（7）对多个装置重复上述步骤经行标定。

按照上述步骤分别对6个量测装置进行标定，标定结果见表1和图5。

表1 装置标定数据表

图5 应变与位移关系曲线

可以看出，在小梁的线弹性工作范围内，梁端位移与截面应变成线性关系。表中0.1~0.5 mm为加载范围，也是梁端的实际位移，应变值与分辨率的积值为测量值，通过测量值与经标定的千分表读数间的差值确定该装置的精度，精度分析结果见表2。

表2 装置标定精度计算表 mm

装置的测量误差绝对值多数为0.001 mm和0.002 mm，将表中所有差值的绝对值平均数作为精度的范围，通过计算的测量精度为±0.002 mm。

4 误差分析

用该装置量测的误差主要有结构曲率误差、安装误差、应变读数误差、标定误差等。

（1）结构曲率误差。在原理中，结构断面的左右两部分只发生平行错动，因此梁端的位移就等于断面错动量。如图6所示，组合梁受弯时，钢与混凝土界面滑移后，界面两侧结构存在曲率[14]时，由于小梁总有一定的长度，与理想的零间距有偏差，此时，梁端位移与真实的界面滑移由于曲率的原因，将有一定的误差，称之为曲率误差。

图6 组合梁中钢与混凝土界面滑移量测量

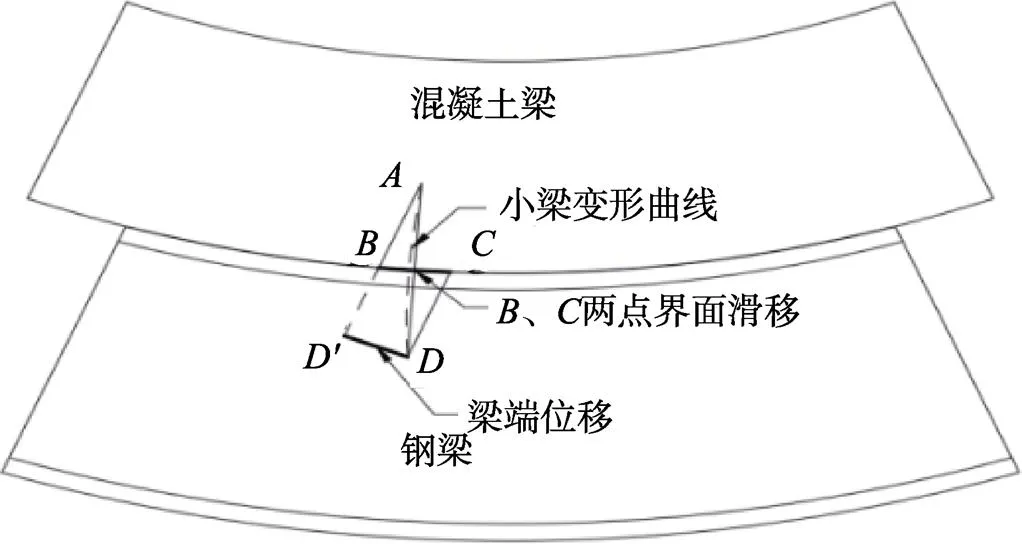
图7 曲率误差示图

图8 滑移测量实物图

（2）安装误差。标定的过程中，位移的施加方向与小梁垂直。将标定好的量测装置固定在断面上方时，因为人为操作，小梁与错动方向垂直度略有偏差，造成安装误差。此种误差可以通过提高安装的精准度来尽量地减小，此误差可以忽略。

（4）标定误差。因为每一个测量装置都需要进行标定确定其精度，当精度较低时，装置的分辨率应采用标定值。在标定过程中需要人为进行读数来控制位移施加的大小，读数的大小存在误差，读数误差导致标定也存在误差。此种误差很小且可以通过提高读数的准确度来减小误差，因此这种可以忽略。

5 结语

[1] 肖岩，彭罗文，KUNNATH S.组合梁考虑滑移效应的理论分析[J].湖南大学学报（自然科学版），2017, 44(1): 77–86.

[2] 陈宗平，应武挡.型钢高强混凝土界面黏结滑移推出试验及其本构关系研究[J].建筑结构学报，2016, 37(2): 150–157.

[3] 刘迎倩.钢-轻骨料混凝土栓钉连接件推出试验研究[J].公路，2018, 63(2): 73–76.

[4] 丁发兴，倪鸣，龚永智，等.栓钉剪力连接件滑移性能试验研究及受剪承载力计算[J].建筑结构学报，2014, 35(9): 98–106.

[5] 李成君，周志祥，黄雅意.装配式组合梁剪力钉滑移性能研究[J].公路工程，2017, 42(2): 111–115.

[6] NILSON A H. Internal measurement of bond-slip[J]. Journal of ACI, 1972, 69 (7): 439–441.

[7] BAN H, MARK A B. Flexural behaviour of composite beams with high strength steel[J]. Engineering Structures, 2013(56): 1130–1141.

[8] 孟祥东，殷志文，陈忠汉.埋入式柱脚粘结滑移性能的试验研究[J].苏州科技学院学报（工程技术版），2011, 24(2): 28–32.

[9] 郝际平，王奕钧，刘斌，等.喷涂式冷弯薄壁型钢轻质砂浆墙体立柱轴压性能试验研究[J].西安建筑科技大学学报（自然科学版），2014, 46(5): 615–621.

[10] 李俊华，薛建阳，赵鸿铁.低周反复荷载下型钢混凝土柱滑移性能试验研究（英文）[J].西安建筑科技大学学报（自然科学版），2008(3): 348–353.

[11] BASEM H AODEL A, Assem A A H. Effect of combining steel fibers with crumb rubber on enhancing the behavior of beam- column joints under cyclic loading[J]. Engineering Structures, 2019(182): 510–527.

[12] 罗永峰，王飞，倪建公，等.弦支穹顶索撑节点滑移性能试验[J].重庆大学学报，2012, 35(4): 65–71.

[13] 杨勇，郭子雄，薛建阳，等.型钢混凝土粘结滑移性能试验研究[J].建筑结构学报，2005(4): 1–9.

[14] 聂建国，沈聚敏，袁彦声.钢-混凝土简支组合梁变形计算的一般公式[J].工程力学，1994(1): 21–27.

Development and application of strain-type cross-section misalignment testing device

FAN Liang1, LI Hongyan1, GUO Sijun2

(1. School of Civil Engineering, Chongqing Jiaotong University, Chongqing 400041, China; 2. Yunnan Investment Holding Group Co., Ltd., Kunming 650000, China)

In order to accurately measure the micro-displacement of structural cross-section and solve the problems existing in traditional measurement methods, a set of testing device for structural cross-section dislocation is independently designed. The device consists of trabecula, fixed end and strain measuring system formed by spring sheet. The resolution and working range of the measuring device are controlled by changing the length and thickness of the trabecula, and the bridge-road combination of the strain measuring system is changed to meet the requirements of the measuring direction. The device can directly measure the staggered momentum between two points in close range, and one-way measurement and two-way dynamic measurement can be carried out. This device has strong applicability and measurement accuracy of (±0.002 mm), and has strong application value.

composite structure; misalignment trace; spring blade

TU398

A

1002-4956(2019)12-0077-04

10.16791/j.cnki.sjg.2019.12.018

2019-04-13

国家自然科学基金项目（51608080）；重庆市自然科学基金项目（cstc2018jcyjAX0509）；云南省交通运输厅科技项目（2018-28）

范亮（1979—），女，安徽芜湖，博士，教授，研究方向为组合结构。E-mail: 27466944@qq.com

李鸿岩（1993—），男，山西阳泉，硕士研究生，研究方向为组合结构。E-mail: 1029897902@qq.com