基于改进BP神经网络的交通图像压缩

田 甜，罗 山

(攀枝花学院交通与汽车工程学院，四川 攀枝花 617000)

0 引言

智能交通的快速发展，大量的交通图像信息需要高效地传输，而图像数据信息量大[1]。因此，采用数据压缩技术来减小图像数据容量，以提高传输的有效性，具有重大的现实意义。

常见的压缩技术有预测编码[2]可以得到较大的压缩比，但是有很明显压缩效率低且算法不稳定缺点；变换编码主要有离散余弦变换[3]、小波变换[4]等，它们可以将能量集中到低频上，但是不能直接通过变换减小数据量；向量量化编码[5]能够得到很高的压缩比，但是这种方法对初始点要求很高，训练时间很长，且存在严重的边缘失真现象。基于BP神经网络的图像压缩[6]，它通过调整隐含层参数以及激活函数来实现压缩，有较强的非线性处理能力，但是它极易陷入局部极小值且收敛速度慢。针对其不足，提出利用LM算法改进BP神经网络，以得到更好的压缩效果。

1 改进BP神经网络原理

1.1 BP神经网络基本结构

BP神经网络由输入层、隐含层以及输出层构成，其中隐含层可以为一层或多层。它属于前馈型神经网络结构，每一层神经元与下一层神经元完全互连，神经元之间不存在同层连接，也不存在跨层连接。图1为一个典型的三层BP网络。

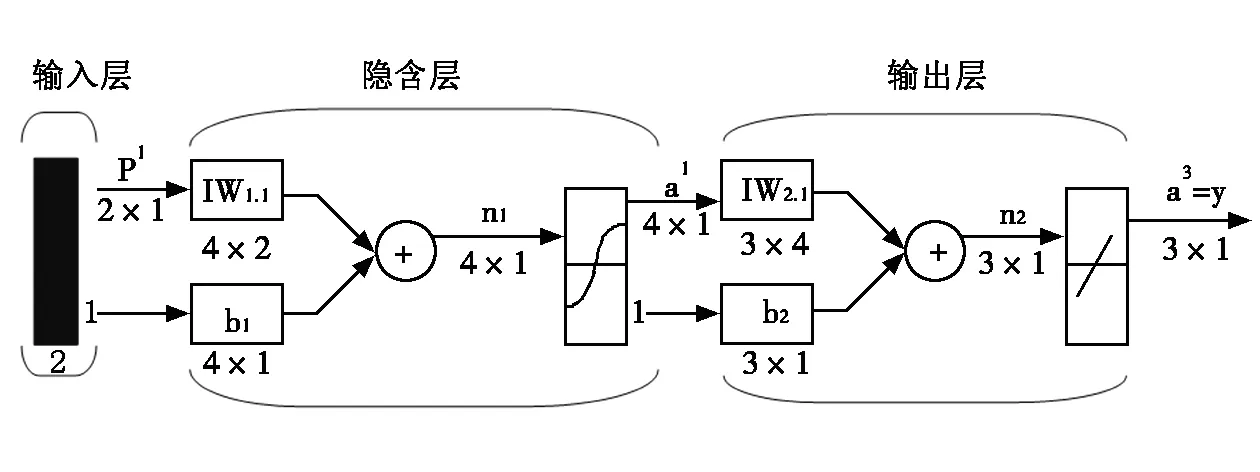
图1 三层BP神经网络结构

其中：p1：输入信号；IW：×R维的权值矩阵(或者S×1的阈值向量)；bn：偏置；y：输出信号。

1.2 BP神经网络训练原理

确定结构之后，要通过网络对输入的样本集进行训练，训练分为两个过程：

1) 信号正向传播：输入信号进入输入层再经由隐含层最后到达输出层产生输出信号。

2) 误差反向传播：误差就是实际输出与最初预期的输出之间的差值，在误差反向传播过程当中，神经元之间的连接权值是由误差反馈进行调节，不断变化的。通过权值的不断修正使网络的实际输出接近期望输出时，训练结束。

1.3 基于LM算法的改进BP神经网络

标准BP神经网络容易陷入局部极小值且收敛速度慢，因此提出利用LM算法改进BP神经网络。LM(Levenberg-Marquard)算法[7]属于一种“信赖域”，其基本思想是：首先确定一个“信赖域半径”，并且，以当前的迭代点为中心，“信任域半径”为半径，确定一个封闭范围。然后，在这一范围内，求解最优点(目标函数的二次接近模型)从而确定“候选位移”。如果候选位移使目标函数的数值大幅度下降，则该位移被视为一种新的位移，且信任域的范围保持或扩大。否则，就表明二次模型与目标函数之间的近似度并不理想，需要缩小信任域的范围，通过解决新的信任域中的子问题来获得新的候选位移。如此重复下去，直至满足迭代终止条件。

2 基于改进BP神经网络的交通图像压缩

2.1 改进的压缩算法

改进的BP神经网络交通图像压缩系统流程如图2所示。

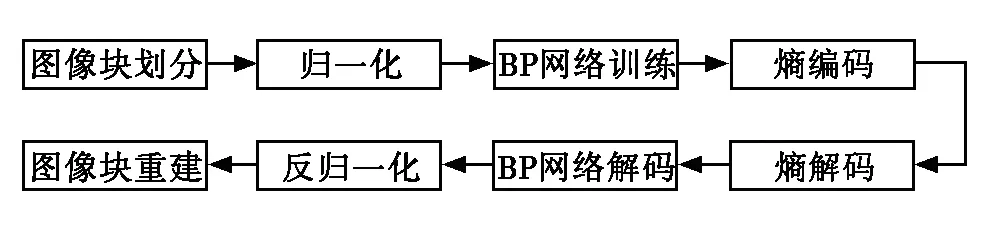
图2 改进BP神经网络交通图像压缩系统

1) 图像块划分。将图像大小调整为128*128，并将图像划分为1024个大小为4*4的图像块，这样输入和输出神经元节点数就确定为16个，将每个图像块作为一个样本向量，保存为16*1024大小的样本矩阵。

2) 归一化。采用均值分布预处理的方法归一化，待处理图像灰度范围为[xmin,xmax]，变换域为[ymin,ymax]，设待处理的像素灰度值为xvalue，则利用式(1)可将原始图像的像素限制于[0,1]内。

(1)

3) BP网络训练与仿真。创建BP神经网络，设置最大允许步数为500，训练目标最小误差为0.001，然后调用train函数进行训练。根据式(2)设置隐含层节点数。

(2)

式中：η为隐层神经元数；a为1-10的常量。

利用LM算法对BP神经网络进行优化训练，设置最大允许步数为500，训练目标最小误差为0.001，然后调用trainlm函数进行训练。调用sim函数对训练结果进行仿真测试。

4) 熵编码。对网络的仿真测试结果进行熵编码，这里采用Huffman编码，以进一步去除统计冗余。

5) 熵解码。对Huffman编码后的比特流进行解码，以便于后续BP神经网络的解码。

6) BP网络解码。当输入一组图像时就会形成一组权值和阈值，此时得到数据为BP神经网络隐含层的神经元输出值。为了重建图像，需要将其输入到网络中，与隐含层和输出层之间的权重矩阵相乘。由于BP网络输出就是它本身，因此在解压缩过程中，将压缩值乘上权值加上阈值就是BP网络解码的输出。

7) 反归一化。将图像反归一化时不需要使用自定义的区间范围，只需将每份数据乘以像素峰值255并取整数即可将每个数据映射到原区间去。

8) 图像块重建。经过块划分后图像矩阵的大小为16*1024，进行块重建时，将矩阵的每列抽取出来，重新排列为4*4矩阵，并对每个4*4矩阵按行排列，则可重建原图像。

2.2 仿真及分析

由式(2)可以确定隐含层节点数取值范围为[6,16]，对不同的隐含层节点数，仿真结果如表1所示。从表1看出，随着隐含层节点数的增加，训练误差有下降的趋势，梯度也越倾斜，在隐含层神经元数为9时，虽然训练误差减小，但是其梯度平缓，达不到收敛状态，因此，仿真实验中隐含层节点数选择8、12和14个。

表1 不同隐层神经元节点数结果比较

对上述设置好参数的改进的网络进行训练，并仿真，结果如下。

在隐含层节点数为8、12和14时，仅从图3—5看不出压缩图像的压缩效果的差异大小。因此，表2给出压缩质量参数对比结果，设置隐含层节点数N为8时，图像的压缩率较高，均方误差较小，因此压缩效果更好。对比GDM-BP算法，经LM算法优化的图像压缩的均方误差很小、压缩率也更大，压缩性能显著提高。

图3 N=8交通图像压缩

图4 N=12交通图像压缩

图5 N=14交通图像压缩

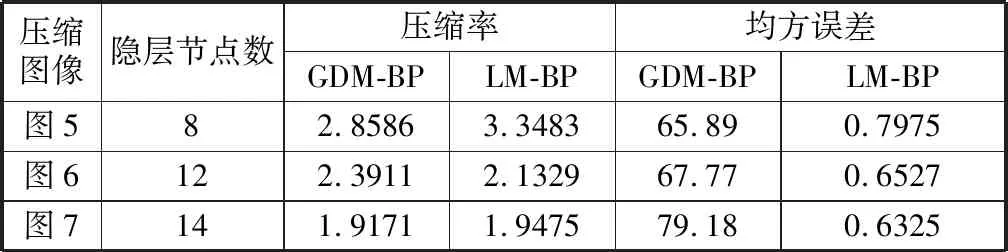
表2 交通图像压缩质量评价参数对比

3 结束语

基于标准BP神经网络的交通图像压缩具有较好的泛化能力，虽然利用最速梯度下降法训练的网络有局限性，但是通过调整训练参数，也可以达到很好的效果；LM算法可以有效解决标准BP神经网络容易陷入局部极小值的问题，并且压缩图像的效果优于标准BP神经网络压缩图像。