基于时空解耦的无人艇编队路径跟踪控制*

廖 刚 徐海祥 余文曌 李文娟

(高性能船舶技术教育部重点实验室1) 武汉 430063) (武汉理工大学交通学院2) 武汉 430063) (江苏科技大学海洋装备研究院3) 镇江 212003)

0 引 言

水面无人艇(unmanned surface vessel，USV)凭借着高速化、小型化、智能化等优势被广泛应用.目前，单水面无人艇取得较多的研究成果[1-4]，但随着无人艇所承担的任务越来越复杂，单艇作业不能满足任务需求，多无人艇之间相互协作，才能更高效率和更高质量地完成任务.如用于环境监测，溢油回收,油气勘探人员搜救[5].在这些任务中，无人艇的期望运动根据要遵循的几何路径和沿路径行驶的期望速度来表征[6].此外，无人艇编队采用的控制方案中，“领导者-跟随者”编队结构形式凭借着其简单性和可扩展性，在实际工程运用中较多.跟随者通过与领导者相互感知和相互协同作用，与领导者保持相似的状态，使多无人艇最终呈现设定的编队队形.

Ihle等[7]设计的控制目标是使无人艇维持在编队预定路径中的期望位置，构造独立的参数变量，使无人艇形成编队.然而该方法在模型试验中，领航者是仿真数据，没有实际运动.文献[6]设计了在未知海流情况下，使无人艇编队沿着设定的直线以恒定航速航行的循迹控制.但是该方法没有考虑曲线路径的影响.徐国焯[8]设计出虚拟结构法和领航者-跟随者法相结合的编队控制方法.在单UUV路径跟踪控制的基础上，完成最终的多UUV编队路径跟踪控制器设计.Peng等[9]利用神经网络和动态表面控制技术设计了鲁棒自适应控制器来解决欠驱动自主地面车辆的编队控制问题.边信黔等[10-11]针对多无人水下航行器的协调路径跟踪控制问题，应用分散控制策略将路径跟踪问题和个体间的速度协调解耦，但是该控制方法不能直接运用于欠驱无人艇.马瑞龙[12]建立了领航者-跟随者编队控制模型，并采用运动学和动力学设计了控制器，实现编队路径跟踪的目的，但是文中无人艇处于没有风浪流的理想环境中，没有考虑无人艇实际航行时外界环境的干扰.齐小伟等[13]利用多智能体聚集模型，基于领航者-跟随者的目标跟踪，实现了含有模型不确定性与未知海浪流干扰项的多无人艇协同编队控制.由于神经网络需要计算出包括风浪流和模型不确定项在内的10个不确定项，对计算性能要求高，很难满足控制在实时性方面的需求.

本文基于时空解耦策略，采用领航者-跟随者模式解决路径变化时的编队路径跟踪控制问题.建立了在不同路径下的编队队形数学模型.将编队路径跟踪控制问题分解为以下两个子问题：每艘无人艇上设计路径跟踪控制器，保证在空间上运动收敛到各自的期望路径；设计速度协调控制器，调整每艘无人艇的运动速度，在时间上实现多无人艇间的协调，保证无人艇的编队队形.仿真实验中，在多路径点过渡过程考虑编队队形相对首向和速度的变化，使过渡过程更加平滑.

1 问题描述

1.1 无人艇数学模型

对于水面无人艇而言，本文主要考虑水平面三自由度运动.采用大地坐标系XOY和随艇坐标系xoy建立无人艇运动和动力学模型，见图1.

图1 无人艇运动坐标系

在参考坐标系下，无人艇的运动模型可以描述为[14]

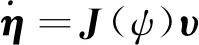
(1)

(2)

τ=Buup

(3)

式中：η=[x,y,ψ]T为无人艇在固定坐标系下的位置及首向；υ=[u,v,r]T为无人艇在随艇坐标系下的纵荡、横荡、首摇速度；M为惯性矩阵；C(υ)为科氏力矩阵；D(υ)为水动力阻尼矩阵；并且假设满足M=MT，C(υ)=-CT(υ)，D(υ)>0，即无人艇是左右舷对称结构；J(ψ)为坐标系转换矩阵，表示为

υr为无人艇在随艇坐标系下相对于流速υc的相对速度，υc和υ的关系为[15]

(4)

其中：tp为推力减额系数；Yδ和Nδ为舵的水动力参数；Tp和δ分别为推进器推力和舵角.

考虑到推进器限制，控制输出作如下限制：

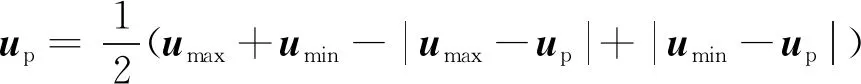
b为无人艇所遭受的外界环境力，主要由风、浪、流组成.

1.2 编队队形数学模型

无人艇编队路径跟踪过程中，除整体有机地进行路径跟踪外，编队还包括：①编队队形的形成问题，即如何使得多无人艇从某种初始是状态下形成符合任务需要的有规律行的有机整体；②编队行进中如何保证队形的稳定不变问题.

多艘无人艇采用领导者-跟随者的编队模式，其中一艘为领航艇，其余为跟随艇.第i艘跟随艇与领航艇之间相对关系为

di=[dxi,dyi,dψi]T

(6)

式中：dxi和dyi分别为跟随艇i在领航艇坐标系中的纵向位置和横向相对位置；dψi为相对首向角，根据设定的路径不同有所差别.

1) 直线路径 在直线路径下，通常跟随艇i的首向角与领航艇的保持一致，即

dψi=0

(7)

2) 曲线路径 在曲线路径下，由于存在曲率半径，则跟随艇i的首向角与领航艇首向角之间的关系为

dψi=2arcsin (dxi/2R)

(8)

式中:R为领航艇所在圆弧路径的曲率半径.

3) 一般路径 对于平面一般路径，可以用含标量θ的参数化表示为ξ(θ).以|dxi|为半径作圆，得到与路径的交点，该点的首向角为切线与OX轴平行线的夹角，也是跟随艇i的首向角.因此，跟随艇i的首向角与领航艇首向角之间的关系：

dψi=ψi-ψl

(9)

三种路径下编队相对关系见图2.

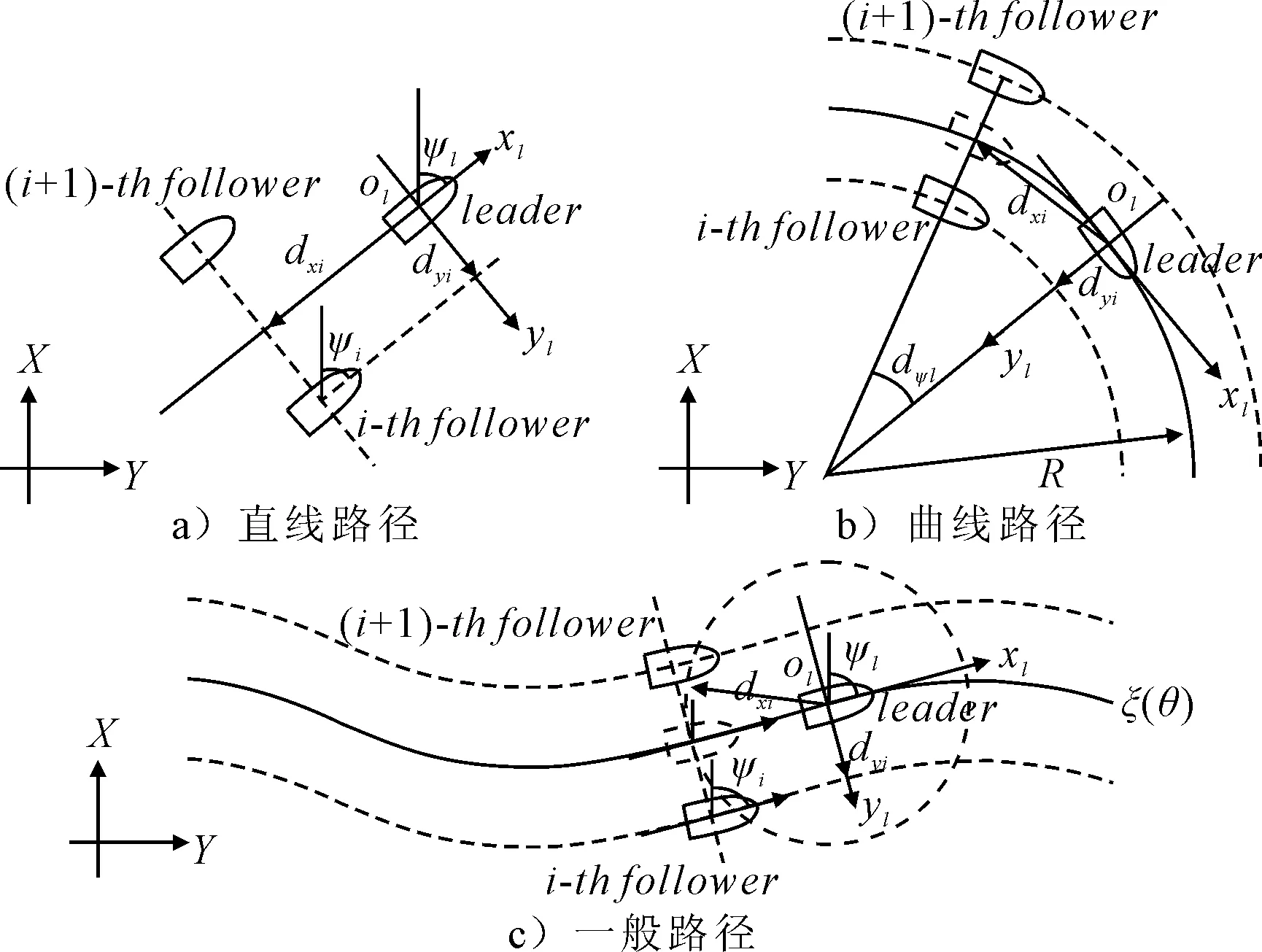
图2 不同路径下编队相对关系

2 控制器设计

2.1 编队偏差

当无人艇偏离设定路径时，需要驱使其回到期望位置，见图3.由图3可知，对于第i艘跟随艇，偏差计算表达式为

(10)

式中：[xei,yei,ψei]T为跟随艇i在自身艇坐标系下的期望位置与实际位置的偏差；[xdi,ydi,ψdi]T为跟随艇i在大地坐标系下的期望位置，可以通过领航艇位置和设定编队队形计算得到；[xi,yi,ψi]T为跟随艇i在大地坐标系下的实际位置.

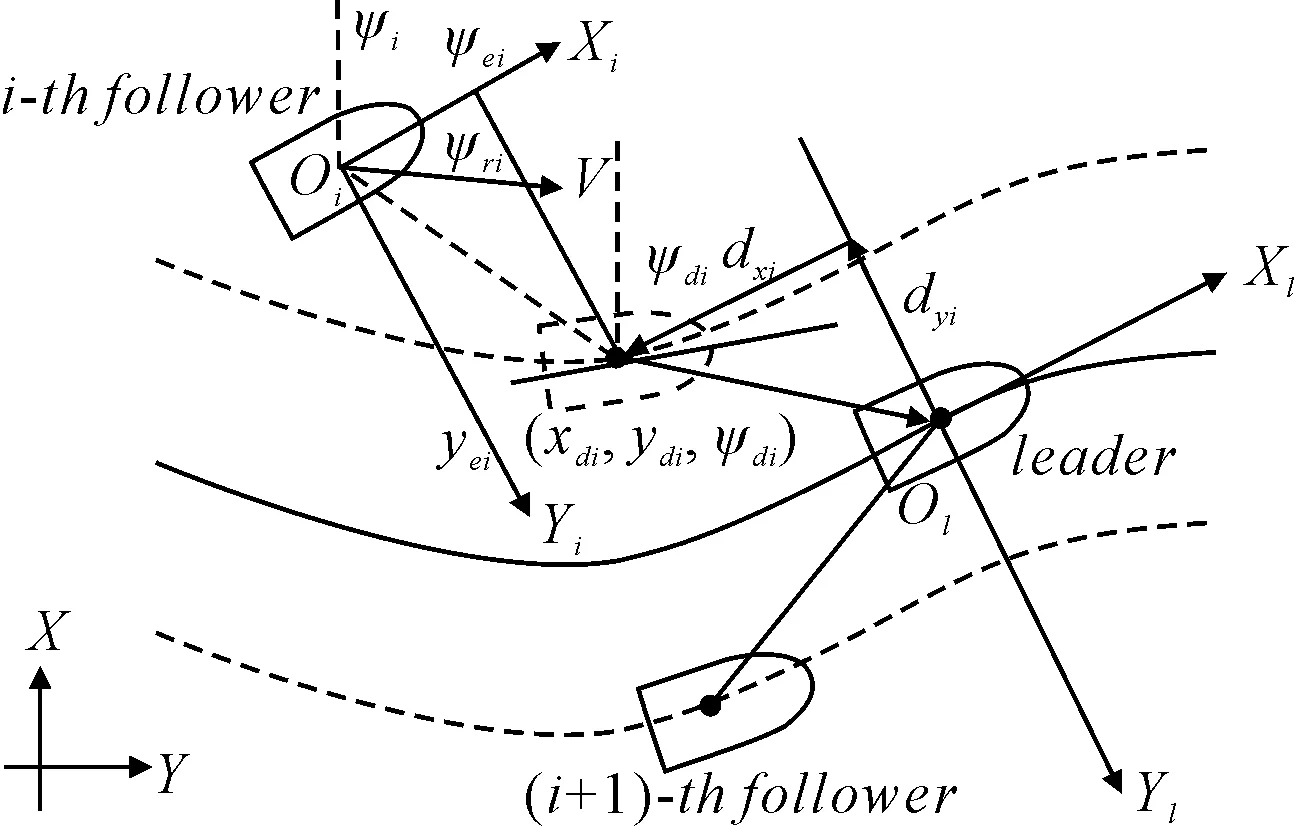
图3 编队偏差图

由图3可知，跟随艇i回到预定路径上的预期首向角为

ψdi=ψri+ψi

(11)

2.2 路径跟踪控制器

路径跟踪控制器主要保证各无人艇在空间上运动收敛到各自的期望路径.

根据式(10)，跟随艇i位置偏差可表示为

(12)

对其微分，则

式中：udi,vdi分别为跟随艇i的期望纵向和横向速度.

该子系统的输入为ui和vi，选取该子系统虚拟控制量为

αui=k1xei+udicosψei-vdisinψei

αvi=k2yei+udisinψei+vdicosψei

(14)

式中：k1,k2>0.

代入式(14)，则式(13)中的ui和vi可以分别被替换成αui和αvi，则式(13)可以改写为

(15)

构造第一个Lyapunov函数为

(16)

明显V1≥0，对V1微分可得

xei(-k1xei+yeiri)+yei(-k2yei-xeiri)=

(17)

由此可知，路径跟踪子系统是渐进稳定的，即

(18)

2.3 速度协调控制器

当无人艇运动预期位置后，需要保证多无人艇首向和速度达到一致并保持稳定.设计速度协调控制器，保证在设定队形下达到一致，实现多无人艇间的协调，而不影响空间域上的路径跟踪性能.

定义投影向量h，首向偏差z1，速度偏差z2为[16]

h=[0,0,1]T

(19)

z1=ψi-ψdi=hTηi-ψdi

(20)

z2=[z2.1,z2,2,z2,3]T=υi-αi

(21)

式中：αi为虚拟控制量，

αi=[αui,αvi,αri]T

(22)

构造第二个Lyapunov函数为

(23)

对V2微分可得

式中：k3>0，并且选取了首向虚拟控制量：

(25)

根据动力学模型(2)和(4)：

因此，式可以改写成

(27)

因此设计控制器如下.

rMSTJT(ψi)υc-(C(υ)+D(υ))JT(ψi)υc-k4z2

(28)

其中，环境适应性参数为

(29)

最终式(24)可转化为

(30)

式中：k4=diag(k4,1,k4,2,k4,3)>0.

由此可知，速度协调子系统是渐进稳定的，即

(31)

2.4 稳定性分析

考虑到控制器包含路径跟踪和速度协调两个子系统，定义起始偏差

(32)

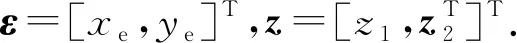
定理1对于光滑的参考路径，设计路径跟踪控制律(14)，并结合首向控制律(25)，速度协调控制律(28)和环境适应律(29)，可以保证关于偏差的系统是渐进稳定的.

证明在路径跟踪控制器中定义了虚拟控制量αui和αvi，在速度协调控制器中定义了虚拟控制量αri，αri可改写成为αri=-k3ψei+rdi.则

(33)

式中：rdi为跟随艇i的期望首向速度.

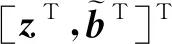
(34)

根据式(31)，该子系统是渐进稳定的.

然后考虑路径跟踪子系统，定义包含误差子系统ε的Lyapunov函数：

(35)

根据式(18)，该子系统是渐进稳定的.

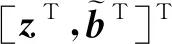
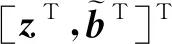
3 仿真分析

为验证编队路径跟踪控制效果，以三艘无人艇作为仿真实验平台，其中一艘为领航者，另外两艘为跟随者.仿真所用无人艇模型采用Cybership-II，其主要参数和水动力导数在文献[14]中有详细介绍.

外界环境力参数见表1，缓变环境力可以通过经验公式[17]计算得到.期望路径通过路径点给出，两线段之间通过圆弧过渡，期望速度等参数见表2.表3为三艘无人艇的初始点位置及编队的相对位置关系.控制器参数见表4.仿真中推进器上下限制值为

umax=[2N,10°]T,umin=-[2N,10°]T

在圆弧阶段，不仅跟随艇i的首向角与领航艇的首向角满足式(8)，而且跟随艇的圆弧切向(纵向)期望速度与领航艇的切向期望速度满足：

(36)

表2 预设路径、相应的转弯半径、期望速度参数

表3 初始位置和编队相对关系

表4 控制器参数

图4 多无人艇运动轨迹及同时刻的相对位置

图5 编队队形相对位置

仿真结果见图4～8.图4为领航艇和跟随艇运动轨迹，以及同时刻的相对位置图.由图4可知，领航艇在根据预设点形成的轨迹上航行，跟随艇按照设定的编队队形航行.图5为领航艇和跟随艇的相对位置.在开始阶段和转向阶段跟随艇需要调整自身位置达到设定值，之后纵向和横向相对位置收敛到设定值.图6为各艇首向角随时间变化曲线.开始阶段，为了沿着设定路径航行，首向角将会被调整.之后跟随艇的首向角将与领航艇保持一致.在领航艇转向时，跟随者的首向角也会改变.转向后，跟随艇的首向角将被调整与领航艇保持一致.由于存在外界环境力，无人艇的首向不是沿着路径的切线方向，但其航向角与路径的切线方向保持一致.图7为无人艇纵向和横向速度.领航艇转向时，位于领航艇转向内侧的跟随艇(第1次转向时的1号跟随艇，第2次转向时的2号跟随艇)的圆弧半径比领航艇的小，因此,速度比领航艇速度小；位于领航艇转向外侧的跟随艇(第1次转向时的2号跟随艇，第2次转向时的1号跟随艇)的圆弧半径比领航艇的大，其速度比领航艇速度大.螺旋桨推力和舵角见图8，推力和舵角在设定的限制值内.为了适应外界环境力，舵角不为零.

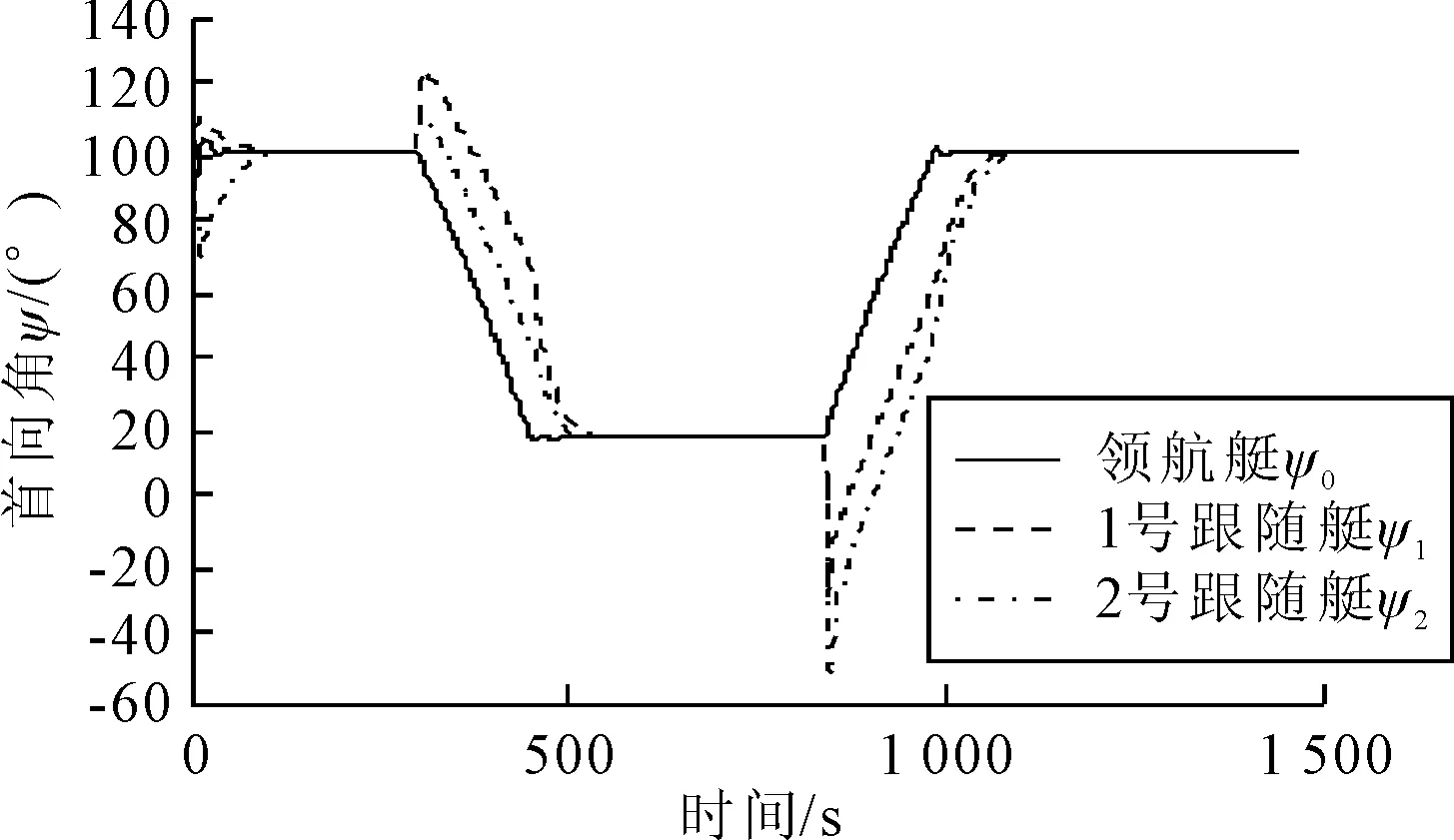
图6 各艇首向角变化图

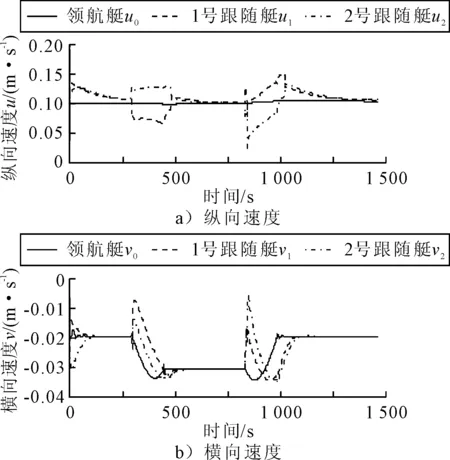
图7 各艇纵向和横向速度变化图

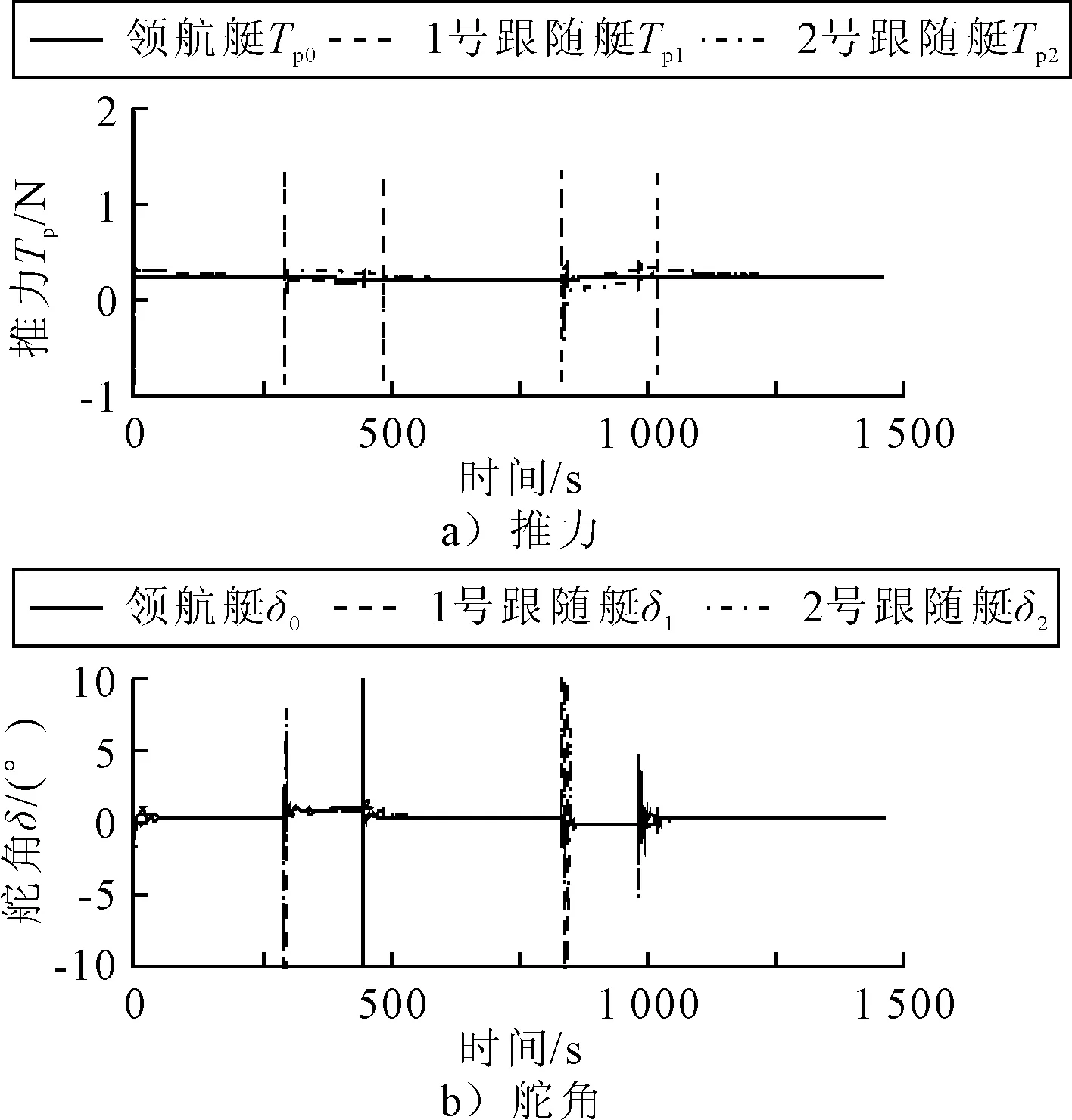
图8 各艇推力和舵角变化图

为验证考虑圆弧过渡并且满足圆弧设定要求的编队路径跟踪控制方法有效性，在相同的控制器参数下，与未考虑圆弧过渡的结果进行对比.图9为两种情况下无人艇轨迹图.由图9可知，在转向过程时，在未考虑圆弧过渡时跟随艇出现转圈的现象(如放大图所示)，主要原因为跟随艇在领航艇坐标系中相对位置超过了设定位置，需要跟随者向领航者的后面运动，同时向后面运动导致横向相对位置变大.两种情况下的编队相对位置见图10a)，考虑圆弧过渡的情况轨迹收敛速度更快且与设定值之间没有偏差.图10b)为两种情况下无人艇航向角变化情况.两种情况都能使跟随艇首向角与领航艇保持一致，但考虑圆弧过渡的情况首向角收敛速度更快.因此考虑圆弧过渡的情况轨迹更加平滑，编队效果更好.

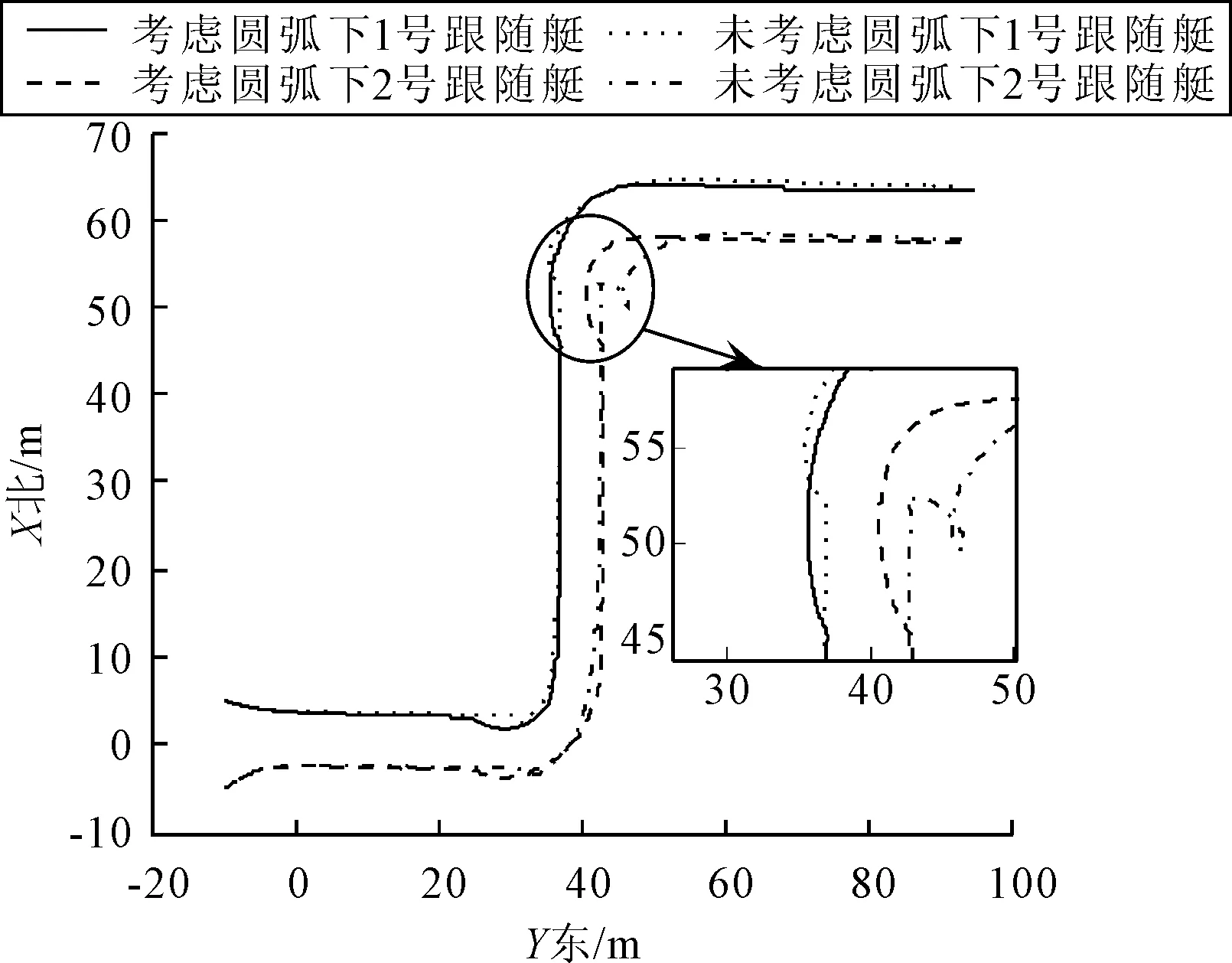
图9 两种情况下编队轨迹对比图

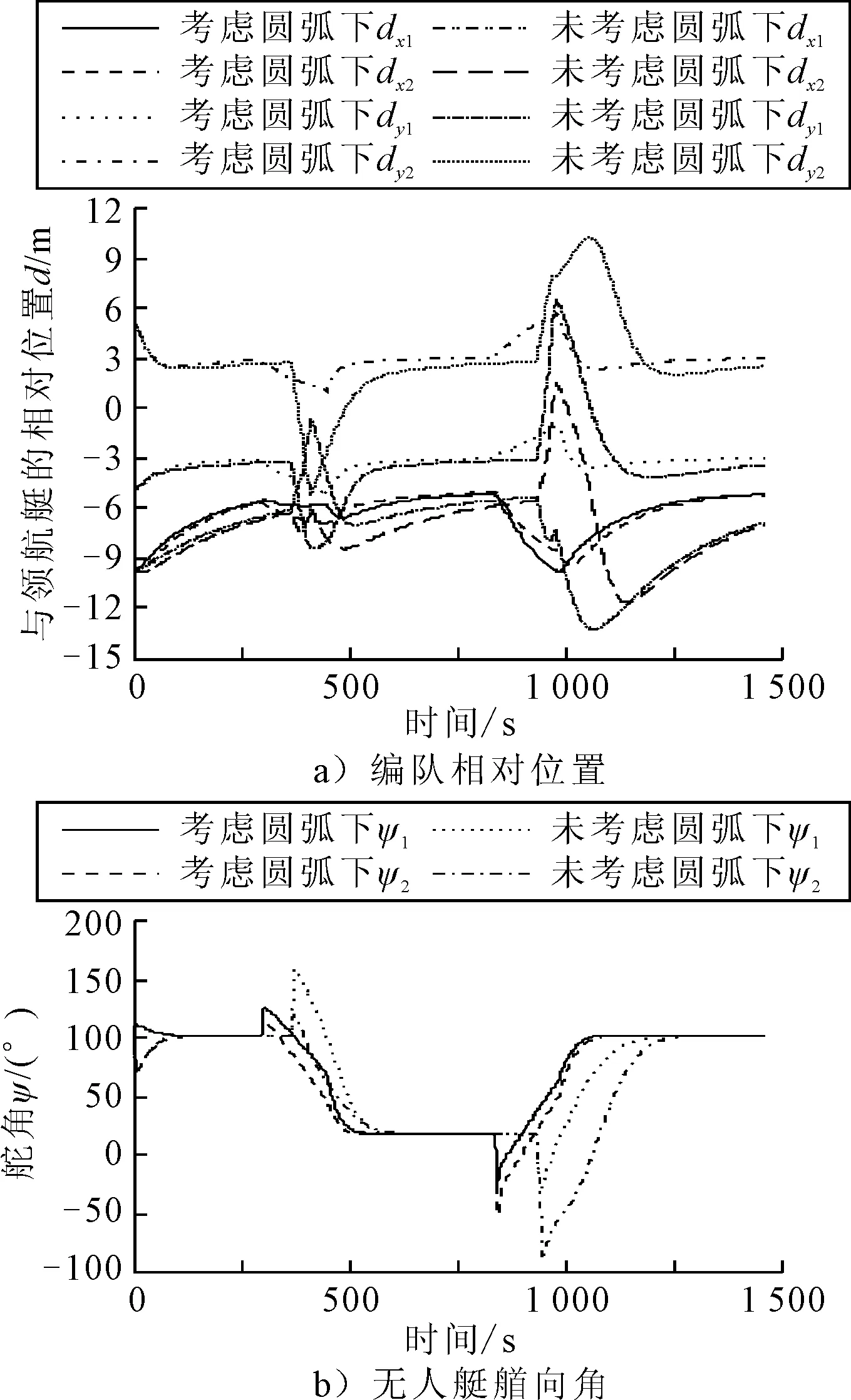
图10 两种情况下编队相对位置和无人艇首向角对比图

4 结 束 语

文中提出一种多点路径的编队路径跟踪控制方法.考虑了不同路径中的编队队形数学模型之间的偏差.基于时空解耦策略把编队路径跟踪控制分解为路径跟踪和编队形成两个子问题.在每艘无人艇上设计路径跟踪控制器，使跟踪误差渐近收敛到零形成编队队形，即空间上满足无人艇在期望路径上运动.同时设计速度协调控制器，来调整自身的运动速度，最终达到期望的速度，在时间上实现多无人艇间的协调，保持设定的队形.采用三艘无人艇进行仿真实验，在多路径点过渡过程中，考虑编队队形中相对首向和速度的变化，其结果比未考虑路径的过渡过程更加平滑.然而控制方法中忽略路径跟踪过程可能出现障碍物，将在后续进行深入研究.