双渠道零售商主导的双回收闭环供应链利益协调
2019-12-27薛立玮
杨 丹 薛立玮
(武汉理工大学物流工程学院1) 武汉 430063) (深圳迈瑞生物医疗电子股份有限公司2) 深圳 518132)
0 引 言
双渠道零售能发挥传统零售渠道和网络零售渠道的优势,创造更多的销售机会,提升零售商需求响应能力.但在双渠道零售环境下,制造商和零售商基于正向销售的利益博弈会被激化,如果同时存在废旧品的回收再制造,则制造商和零售商因逆向回购而引起的渠道利益博弈会加剧,从而导致闭环供应链协调变得更加复杂.
一些学者从制造商的角度研究了双回收闭环供应链利益协调问题.李梅英等[1]研究了制造商主导下的双渠道回收闭环供应链定价模型,李奔波等[2]则针对该类模型提出利用收入共享契约实现制造商和零售商的利润协调;Ma等[3-4]研究了政府行为对双渠道闭环供应链的影响;王玉燕[5]探讨了政府干涉措施下双渠道回收的闭环供应链管理模式,安彤[6]在此基础上研究了制造商双渠道条件下,利用二部定价契约实现政府干涉措施下双渠道销售和回收闭环供应链的协调;吴克晴等[7]研究了线上和线下双渠道回收模式下的多期闭环供应链网络均衡问题,发现该模型能提高制造商和整体的经济效益.还有一些学者从第三方回收的角度研究了双渠道闭环供应链协调问题.许茂增等[8]研究了基于第三方回收的双渠道闭环供应链协调机制,构建了制造商网上直销、零售商传统渠道销售的双渠道闭环供应链决策模型,设计通过利润共享-费用分担契约实现分散决策下双渠道闭环供应链的协调;林杰等[9]针对第三方与制造商共同负责回收的双渠道销售和回收的闭环供应链,分别以制造商和零售商为博弈主导者建立了闭环供应链定价模型,研究发现废旧品第三方回购价、制造商直接回购价、制造商第三方回购价不仅取决于市场力量结构,还取决于顾客对第三方回收价的敏感程度;郝新军等[10]研究了第三方和销售商共同回收的闭环供应链模型,利用补偿契约-成本分摊契约实现分散决策下供应链协调;丁雪峰等[11]针对第三方、零售商共同回收的双回收闭环供应链决策问题,研究了制造商对零售商与第三方回收商采取的歧视性回收定价策略,利用歧视系数对比讨论了歧视回收与公平回收策略下的供应链协调问题.
目前,对双渠道销售条件下由零售商主导的双回收闭环供应链协调研究的文献还不多见.姚锋敏等[12]构建了由一个占主导地位零售商、一个制造商及一个第三方回收商组成的闭环供应链决策模型,认为在零售商主导的闭环供应链中,当第三方有利可图时,第三方负责回收对零售商是占优策略;相对于第三方负责回收,由零售商负责回收对制造商和整个闭环供应链系统均是占优策略.梁喜等[13]研究了零售商主导市场下的具有竞争性的双渠道回收闭环供应链问题,建立了制造商和零售商回收、制造商和第三方回收以及零售商和第三方回收的三种混合回收闭环供应链模型,对比发现制造商和零售商共同回收的模式为最优,且批发价、零售价与竞争强度呈正向关系,回收率、成员利润,以及供应链总利润与竞争强度呈反向关系.文中在加入随机需求因子的基础上,建立了零售商双渠道销售、制造商和零售商共同负责回收的闭环供应链博弈模型,设计并验证改进的二部定价契约对供应链系统的协调机理,为双渠道闭环供应链协调管理提供决策依据.
1 模型描述和基本假设
根据赛诺发布的《2017年手机回收市场研究》显示,2014—2017年,我国废旧手机存量约18.3亿台,再利用潜在价值超6 000亿元.通过对废旧手机再利用、翻新零部件,以及原材料回收等,企业可以大幅度降低物料成本,创造更大的利润空间,例如,2015年苹果公司从近4万t的废旧iPhone、iPad和iMac中,拆解出重约2.8万t、价值约2.53亿人民币的可再次利用材料.以手机这一电子产品为研究对象,为了简化模型计算过程,构造出由单个制造商和处于寡头垄断地位的单个双渠道零售商所形成的二级闭环供应链模型,其中零售商同时采用传统渠道和网络渠道进行手机零售,制造商在生产新手机的同时也对自身回购或零售商回购的废旧手机进行再制造,供应链系统结构见图1.
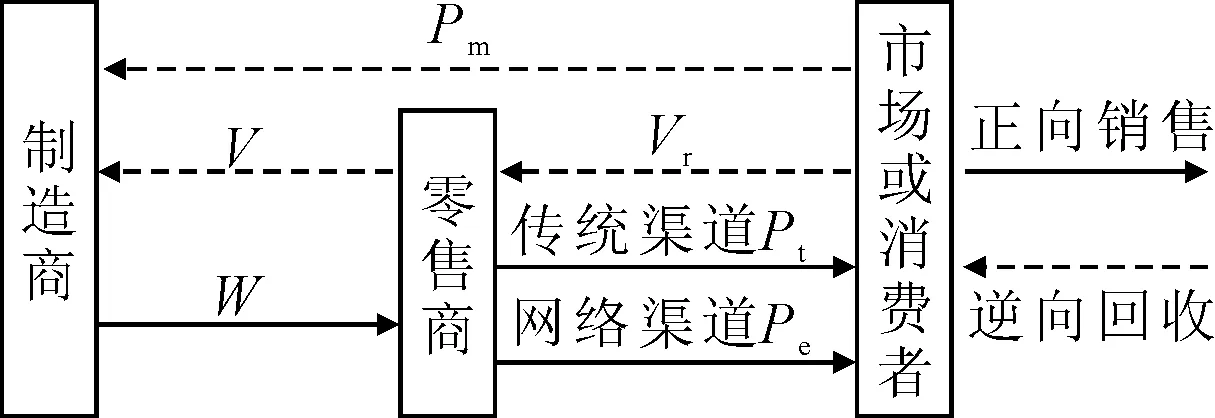
图1 闭环供应链系统结构图
为了便于更清晰地理解模型,对双渠道零售商闭环供应链模型构建中涉及的基本变量和参数进行以下说明:C为新手机的单位生产成本;Cr为再制造手机的单位再生产成本;l为直接回收方的额外单位回收成本(包括废旧产品的收集、运输等费用);W为制造商给零售商的批发价;Pt为零售商传统渠道的手机零售价;Pe为零售商网络渠道的手机零售价;Pm为制造商给顾客的废品单位回收价;V为制造商给零售商的废品单位回收价;Vr为零售商给顾客的废品单位回收价;Dt为零售商传统零售渠道的手机需求量;De为零售商网络零售渠道的手机需求量;Πi为供应链企业i的利润,其中:i∈{M,R,S},M为制造商、R为零售商、S为供应链系统.
为确保决策科学性和分析简便性,对模型进行如下假设说明.
假设1制造商和零售商之间是主从博弈关系,均考虑自身利润最优下制定决策.其中处于寡头垄断地位的零售商是供应链的主导者,面向制造商定制并包销全部特定手机,且具有拟定契约的权力;制造商作为供应链跟随者,只有接受或拒绝该契约的权力.
假设2市场需求是不确定的,供应链节点之间的基于契约的信息对称,制造商和零售商都是完全理性和风险中性的.
假设3制造商按照零售商定制化订单生产特定手机,且该手机的市场潜在总容量为ɑ,传统零售渠道和网络零售渠道的市场占有率分别为λ和1-λ,两种渠道的需求均为随机函数.
假设4回收的废旧品均能进行再制造,且再制造品与新商品不存在明显的性能差异,在合适的折扣条件下,顾客对两者的态度相同.
假设5为保证废旧品的回收再制造对供应链所有企业都是有利可图的,则制造商回收再制造节省的单位成本Δ应大于其从回收方收购的单位回收价,即满足0 假设6参照Park等[14]构造的双营销渠道的需求函数模型,假设废旧品的回收量是仅与回收价相关的函数,制造商直接回收量为SM=β(Pm-Vr),零售商回收量为SR=s+αVr+β(Vr-Pm),其中s体现了顾客自愿无偿归还的废品数目;α为考虑制造商和零售商回收价格差敏感系数后顾客对零售商回收价格的敏感系数;β为顾客对不同回收渠道回收价格差的敏感系数对废品的回收价格敏感系数,且满足α,β>0.在双回收模式下,顾客会因为零售商回收的便捷性更倾向于这种回收方式,因此只有制造商给予顾客的回收价高于零售商给予顾客的(即Pm>Vr),制造商直接回收方式才有效. 以双渠道模式的线性需求函数为基础[15-16],对两个零售渠道下的需求函数都引入了随机需求因子,得到具体期望需求函数为 (1) 式中:μt和μe分别为两种零售渠道的市场随机需求量,分别在[mt,nt]和[me,ne]范围内服从均匀分布;θ为同种零售渠道内的需求价格弹性系数;γ为两种零售渠道间的需求价格交叉弹性系数,表示由于一个渠道零售价比另一渠道更低廉,从而导致顾客从原有购买渠道转向该渠道,且满足θ>γ>0.同时,假设zt和ze分别为零售商两种零售渠道的库存水平;ht和he分别为零售商两种零售渠道的单位库存成本;st和se分别为零售商两种零售渠道的单位缺货成本. 在该模型中,各方均以自身利益最优为依据进行决策.此时,由于零售商作为决策中的主导者,具有优先权,根据Stackelberg博弈思想,零售商会先确定自己的价格策略,然后制造商再进行相应的价格决策.在求均衡解时,采用逆向归纳法,即先根据制造商的利润函数求出其反应函数,而后根据该反应函数求出零售商的利润函数.故为求解模型,将零售商的决策变量Pt,Pe换算成单位零售利润Mt,Me与批发价W的函数,将回收方的决策变量Vr换算成单位回收利润Mr与制造商回收价V的函数,即 (2) 由此可知,制造商和零售商的期望利润函数为 E(ΠM)=(W-C)(E(Dt)+E(De))+ (Δ-Pm)SM+(Δ-V)SR (3) E(ΠR)=MtE(Dt)+MeE(De)+ (V-Vr)SR-Y (4) 定理1E(ΠM)是关于(W,V,Pm)的严格三元联合凹函数. 证明通过对E(ΠM)求关于W,V和Pm的导数,可知的海塞矩阵为 其行列式的各阶顺序主子式分别为 |HM|1=-4θ<0,|HM|2=8θ(α+β)>0, |HM|3=-16θαβ<0 显然该海塞矩阵是负定的,即E(ΠM)是关于(W,V,Pm)的严格三元联合凹函数. 根据定理1,先对E(ΠM)分别求关于W,V和Pm的一阶条件,得到制造商的反应函数和最优回收价为 (5) (6) (7) 将式(5)~(7)代入式(4)求关于Mt,Me和Mr的一阶导数便可得到商品传统渠道和网络渠道的预期单位零售最优利润,以及单位回收最优利润为 (8) 将式(8)代入反应函数(5)~(7)可得商品的最优批发价和制造商给零售商的最优回收价为 (9) 进而可得出:零售商传统零售渠道和网络零售渠道的商品最优期望需求量和最优零售价、零售商给顾客的最优回收价以及商品的最优回收量分别为 (10) 最后,将求得的所有决策参数最优值分别代入式(3)~(4)可得到分散决策条件下制造商、零售商以及供应链系统的最优期望利润为 (11) (12) 在该模型中,供应链各成员企业不再只以自身利润最大化为决策目标,而是作为一个整体,以供应链系统的利润最优为最终目标进行决策,供应链系统结构见图2.此时决策变量为Pt,Pe,Vr和Pm,整条链的期望总利润函数为 E(ΠS)=(Pt-C)E(Dt)+(Pe-C)E(De)+ (Δ-l-Pm)SM+(Δ-Vr)SR-Y (14) 图2 集中决策下闭环供应链系统结构图 通过式(14)海塞矩阵可知,供应链期望总利润是E(ΠS)是关于Pt,Pe,Vr和Pm的四元联合凹函数,因此,分别对式(14)求关于Pt,Pe,Vr和Pm的一阶条件,且令其为零可得到集中决策模型下的最优定价策略. (15) 将式(15)代入式(1)可得到商品传统渠道和网络渠道的最优需求量. (16) 将求得的决策参数最优值代入式(14)可得到集中决策条件下供应链系统的最优期望利润为 (17) 证明将集中决策下的供应链期望总利润减去分散决策下供应链期望总利润,可得: (18) 命题1表明,在分散决策情形下,由于制造商和双渠道零售商并不像集中决策情形下那样作为一个统一的决策整体以供应链总利润最优为决策目标,而是以二者各自的利益最优进行独立决策,因此会引起整条供应链中存在“双重边际效应”,以至于极大削减了供应链总利润,使其无法实现集中决策下的获利水平,即协调状态.因此,要使分散决策下的供应链实现上述状态,需要设计一个合理的契约来改变制造商和零售商的决策行为,实现以供应链总利润最优为目的的决策. (19) (20) 命题2在双渠道零售商闭环供应链中,只有当产品的批发价格Wb、制造商给零售商的回收价Vb和零售商补偿给制造商的转移支付费用L满足式(21)的条件时,二部定价契约(Wb,Vb,L)才能得到有效执行,从而完成供应链的有效协调,保障企业双方实现共赢. (21) 其中: (22) 证明在实际的供应链优化过程中,制造商与零售商只有在确保执行契约后双方的期望利润水平均大于分散决策情形时,才会同意采用该契约,即如果要使契约有效执行,则须满足: (23) 将集中决策下所求得的各均衡解代入式(19)~(20)后,再代入上述不等式即可求解得证. 命题2表明,在实际运营中,制造商与零售商只需通过一个二部定价契约(Wb,Vb,L),便可通过灵活商定契约参数Wb,Vb以及L的取值,形成供应链利润在两者间的自由组合,实现双方均有效提升获利空间的同时完成整条供应链的利益协调. 为了进一步探讨产品批发价Wb、制造商给零售商的回收价Vb和零售商转移支付费用L对二部定价契约协调前后双方期望利润差的影响,对模型中相关参数进行数值模拟研究.具体赋值为 C=20,Cr=8,l=2,Δ=10,ɑ=500, λ=0.6,θ=5,γ=3,s=1,α=0.3, β=0.5,μt=2,μe=3,st=se=15, ht=he=10,zt=ze=1 将上述参数值分别代入分散决策中制造商与零售商的最优期望利润函数式以及式(18)~(19),通过作差可得到契约协调前后双方期望利润差各自为 (24) 同时由式(21)~(22)可得制造商给零售商的回收价的取值范围为:0 图3 L,Wb对协调后制造商和零售商利润差的影响 由图3可知,不论是商品的批发价Wb还是补偿给制造商的转移支付费用L越高,协调后零售商所能获取的利润均呈线性递减趋势,但制造商所能获取的利润却呈线性递增趋势,即制造商期望利润与商品批发价Wb和转移支付费用L均成正相关,而零售商期望利润则与商品批发价Wb和转移支付费用L均成负相关.显然,在实际运营中,由于商品的批发价升高,制造商所能获取的单位商品利润的便会有所增加,而零售商所能获取的单位商品利润则必然会减小.同时,商品的批发价Wb对协调前后双方期望利润差的影响要远大于转移支付费用L对协调前后双方期望利润差的影响.因此在制定契约时,制造商与零售商需谨慎商定商品的批发价,确保双方获利的最优化. 以上算例验证了通过合理调整二部定价契约的契约参数Vb,Wb及L的取值,即可保证协调后制造商与零售商的期望利润均大于原来分散决策下的利润水平,但每个供应链成员的利润分配比例依赖其市场竞争力和相互间的讨价还价能力,从而证实了该契约对双渠道零售商主导下的双回收闭环供应链的有效性. 在双渠道零售商主导的前提下,探讨了随机需求下制造商和零售商共同负责废旧品回收的双渠道闭环供应链利益协调问题.通过对比分散决策与集中决策下的均衡解和成员企业最优利润,发现分散决策下由于双边际效应造成的渠道冲突问题,从而导致系统的总获利小于集中决策下的获利水平.因此,利用改进的二部定价契约对双渠道零售商闭环供应链分散决策模型完成协调优化,并得出了各协调参数的适用范围.同时,通过数值模拟分析了商品批发价Wb和转移支付费用L对二部定价契约(Wb,Vb,L)协调前后制造商和零售商期望利润差的影响,研究结果表明:①制造商的利润伴随二部定价契约参数Wb和L的变大而线性提高,零售商的利润则伴随Wb和L的变大而线性衰减;②商品的批发价Wb对协调前后双方期望利润差的影响要远大于转移支付费用L对协调前后双方期望利润差的影响. 为了简化模型计算过程,文中只考虑了由单个制造商、单个零售商构成的单寡头垄断模型,但在实际的运作中,供应链上会同时存在多个同类企业.这种情况下,企业之间就会存在纵向的或横向的合作竞争关系,模型会相对复杂,在研究时要综合考虑双向冲突问题,因此,在将来的研究中可以进一步将该模型扩展延伸.2 基本模型
2.1 分散决策模型
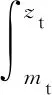

2.2 集中决策模型
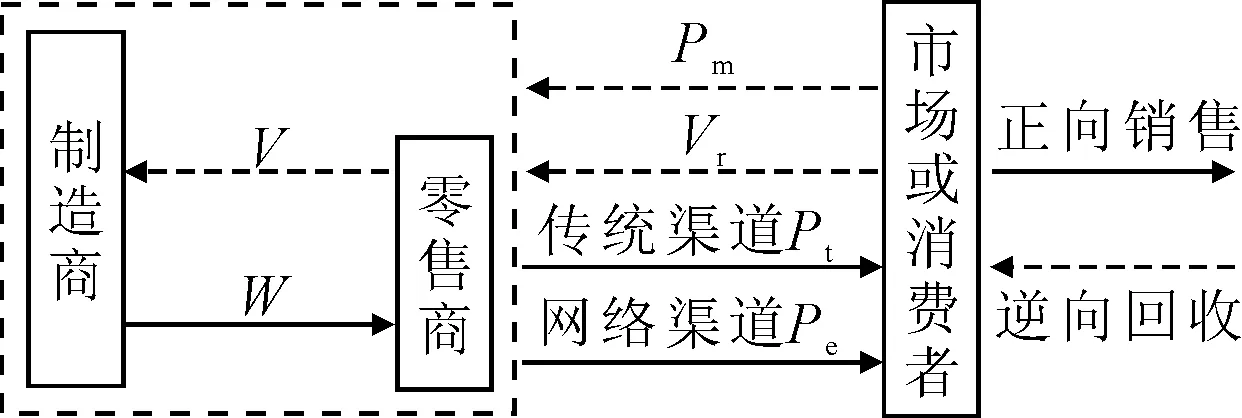
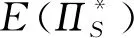
3 契约协调模型

4 数值模拟

5 结 束 语
