过车记录缺失下的瓶颈路段流量分析*
2019-12-27朱海峰刘彦斌温熙华韦学武陈鹏飞
刘 畅 朱海峰 刘彦斌 温熙华 韦学武 陈鹏飞
(中电海康集团研究院 杭州 310012)
0 引 言
交通数据是交通监测与控制的基础.但因检测器覆盖率低、损坏、传输延迟等问题,获取到的交通数据常常存在缺失,无法满足配时优化的需求.选用可靠的方法对缺失数据进行补全,能够提高数据的完整性和可用性,更好地服务于交通管理和决策.
交通数据具有时空相关性,对缺失数据修复即是根据已有数据和缺失数据的时间或空间相关性对缺失数据进行满足一定可靠度的估计或预测[1].Wei等[2]采用K均值聚类技术,对具有相似交通流模式的路段进行分组.针对每组路段构造了一个基于叠加去噪自编码的深度学习模型用于预测缺失的数据点.Asif等[3]提出了基于矩阵和张量的方法,通过提取大型路网中常见的交通模式来估计缺失数据的值.Tak等[4]利用改进的K近邻算法实现了一种基于路段时空相关性的数据插补方法.该方法能够对一条路段上多个相互关联的检测器的缺失数据同时进行修补.吴坚等[5]基于空间自相关分析方法和RBF 神经网络拟合相结合的方法对交通流残缺信息进行修补.刘家东[6]通过分析卡口数据缺失的原因,提出了基于时间序列、基于历史数据以及基于空间位置的旅行时间数据修复方法.杨帅等[7]基于卡口数据针对出行车辆的旅行轨迹不完整现象,建立了一种OWA算子和TOPSIS算法相结合的轨迹重构模型.王龙飞等[8]结合调查点布设方案、路网拓扑结构、车辆行经各调查点的时距关系以及车辆路径选择行为,提出了一种基于车牌照信息的丢点轨迹还原方法.高子玉[9]基于监控视频数据,以车辆换道次数、加速度变化及安全距作为A*算法决策函数重构道路交通流.陈浩然[10]分析了卡口数据的特性,介绍了基于卡口数据的路段车流行程速度的计算方法,并对异常数据和缺失数据进行了剔除和修复.
文中基于电子警察数据提出了一种过车记录缺失下的瓶颈路段流量分析方法,用于分析路段流量关系,确定造成瓶颈产生的关键路段,制定瓶颈控制、区域控制方案.
1 路段关联度
瓶颈路段指早晚高峰期间易出现过饱和状态、其车辆排队长度约等于路段长度的路段或由事故和突发流量引起的、车辆排队长度约等于路段长度的路段[11].瓶颈若不能得到及时消散,会引起排队蔓延,造成路网瘫痪[12].瓶颈控制的关键是分析瓶颈路段流量的来源和去向,从而对上游限流、下游泄流,达到疏散瓶颈的目的.关联度作为衡量路段与瓶颈之间关系的指标,为在时间段T内,通过上游路段且进入瓶颈路段的车辆数与瓶颈路段车辆数的比值,或通过下游路段且从瓶颈驶出的车辆数与瓶颈路段车辆数的比值.所以上游路段与瓶颈路段的关联度为
(1)
式中:b为瓶颈路段;a为瓶颈上游路段;αa,b为路段a与瓶颈b的关联度;Qin为时间间隔T1内驶入b的总车辆数;Qa,b为在时间间隔T2内从a驶入b的车辆数.T1,T2的参考取值分别为:5,20 min.下游路段与瓶颈的关联度为
(2)
式中:c为瓶颈下游路段;αb,c为瓶颈路段b与路段c的关联度;Qout为时间间隔T3内驶出路段b的总车辆数;Qb,c为在时间间隔T4内从b驶入c的车辆数.T3,T4的参考取值分别为:15,5 min.在路口检测设备完好,能够获得每辆车的过车记录时,可以很容易地通过匹配车牌信息,获得关联度.在路口检测设备缺失,获取不到通过的车辆数时,无法计算关联度,判断上、下游路段与瓶颈路段的关系,故需要利用补全算法通过已知数据推出未知数据,提高数据的完整性.补全步骤为:①根据每辆车的过车记录,补全车辆的行驶轨迹;②计算每条路段的转向流量,根据转向关系补全和修正流量数据;③根据路网的静态数据和动态数据,存储每条路段上、下游的路段编号和各个转向的流量情况,标记数据缺失路段;④在瓶颈被识别后,计算瓶颈上下游与瓶颈路段的关联度,根据瓶颈出现的位置对路段进行分层.⑤遍历分层结构,根据数据缺失路段所在的层级、位置及其与其他路段的关系,将缺失的关联度数据进行补全和修正.
2 过车记录补全
电子警察又称智能交通违章监摄管理系统,通常安装在信号控制交叉口,对机动车的违章行为实现全天候监视,捕捉车辆违章图文信息.每辆通过装有电子警察的交叉口的车辆都会在数据库中产生一条过车记录,至少包含:过车时刻、车牌号码、交叉口名称、车道编号、方向等信息.通过对过车记录进行统计,可以获得交叉口的总流量,方向流量,转向流量,过车记录见表1.

表1 过车记录
在城市道路中,除信号控制交叉口外还有部分无信号控制交叉口,一般没有检测设备,给交通数据分析造成困难.文中所述的缺失,指没有检测设备造成的数据缺失,已知数据缺失点的位置和数量.
图1为过车记录缺失示意图, 1和3为信号控制交叉口,各个方向均布设有电子警察,2为无信号控制交叉口没有视频检测设备.车辆依次通过交叉口1,2,3在数据库中只产生两条记录,此时可以根据路段邻接关系进行过车记录补全.

图1 过车记录缺失示意图
路段邻接关系存储在数据库中,每条数据至少包含路段编号,车道数量,起始交叉口编号,终点交叉口编号,方向,路段信息见表2.

表2 路段信息
因路段关系明确,且每条过车记录都清楚地标记了车辆所在车道和方向,若相邻两条过车记录之间只缺失一个点位,可以准确地补出缺失轨迹所在位置,见图2.
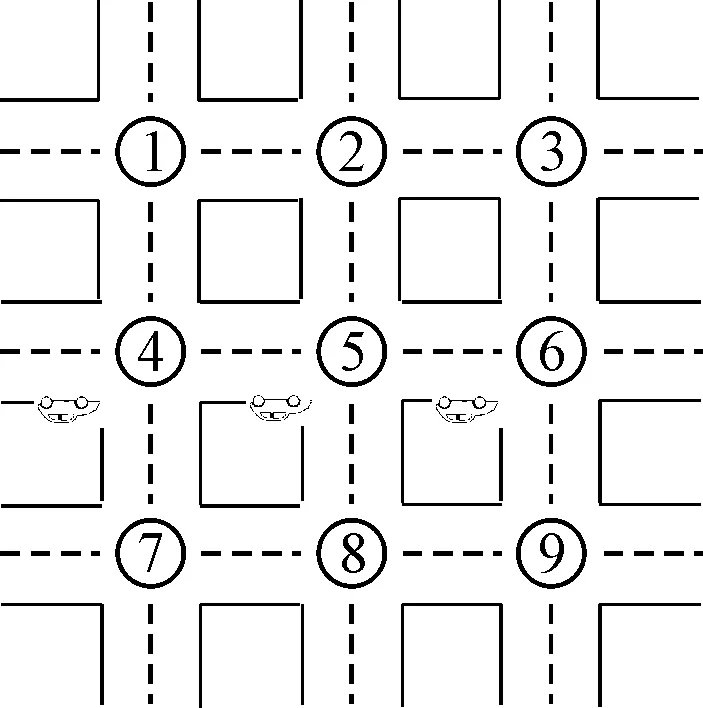
图2 缺失一个点位补全示意图
由图2可知,9个交叉口,其中交叉口5数据缺失,若通过查询发现车辆的轨迹为交叉口4西向东直行,交叉口2南向北直行,则可以判断出中间缺失过车记录为交叉口5西向东左转;若轨迹为交叉口4西向东直行,交叉口6西向东直行,则可以判断中间缺失过车记录为交叉口5西向东直行;若轨迹为交叉口4西向东直行,交叉口8北向南直行,则可以判断中间缺失过车记录为交叉口5西向东右转.在确定车辆位置后,可以根据路段长度估计车辆通过数据缺失交叉口的时刻.设车辆通过交叉口4的时刻为t1,通过交叉口6的时刻为t2,交叉口4和5之间路段长度为L1,交叉口5和6之间路段长度为L2,那么车辆通过交叉口5的时刻为
(3)
若两条过车记录之间缺失的点位数大于1,则可能有不止一条可行路径存在,需要根据最短路算法补全车辆行驶轨迹.考虑到实际路网中因出行者对行程时间和路段长度估计的偏差,不会全部选择最短路,故采用K最短路算法[13],以路段长度为权值,筛选出k条备选路径,并按照Logit模型[14]以一定概率进行路径选择,补全路径上缺失点位的过车记录.算法步骤为
步骤1查询过去T时段内的所有过车记录,根据车牌匹配出每辆车的行驶轨迹,并按时间先后顺序存储过车记录.
步骤2对每辆车,参考路段信息依次检查相邻的两条过车记录是否属于有邻接关系的路段.若前一条记录的终点交叉口编号和后一条记录的起始交叉口编号相同,则判断路段相邻,数据正常;反之,则判断中间有点位缺失.
步骤3根据路段邻接关系确定缺失点位个数.若缺失的点位数为1,按照路段邻接关系进行过车记录补全;若缺失点位数大于1,按照K最短路算法和Logit模型在路径选择后补全过车记录.
3 流量数据修正及补全
在过车记录补全完成后,数据得到了一定程度的恢复,但受车牌识别率限制,部分车辆在通过交叉口时留下了过车记录,但没有被识别出车牌号[15],见表3.
过车记录补全只能填补识别到车牌的车辆轨迹,而无法处理不能识别到车牌的数据,所以补全的流量q′通常会小于其真实值q,因此,需要进一步根据路段转向关系对流量数据进行修正,见图3.

表3 没有识别出车牌的过车记录

图3 流量关系示意图
若交叉口检测器完全,由图3可知,流量应为
qh1+qa2+qf3=qb
(4)

(5)
(6)
同理,若式(4)中有三个流量是缺失的,也按比例进行修正.
若在过车记录补全之后,仍然有部分路段没有流量,由图3的转向关系可知,利用真实流量数据q,补全的流量数据q′,推导出二次补全的流量数据q″.
至此,利用空间信息对补全的过车记录统计得到的流量进行修正,同时对过车记录无法补全的部分,进行流量补全.
4 路段关联度修正及补全
4.1 路段数据存储
每条路计算并存储见图4.

图4 路段数据存储结构
图5为路段数据信息,以图5中路段b为例,上游共3条路段,右转路段编号a1,转向流量Qa1;直行路段编号a2,转向流量Qa2;左转路段编号a3,转向流量Qa3.下游共3条路段,右转路段编号c1,转向流量Qc1;直行路段编号c2,转向流量Qc2;左转路段编号c3,转向流量Qc3.
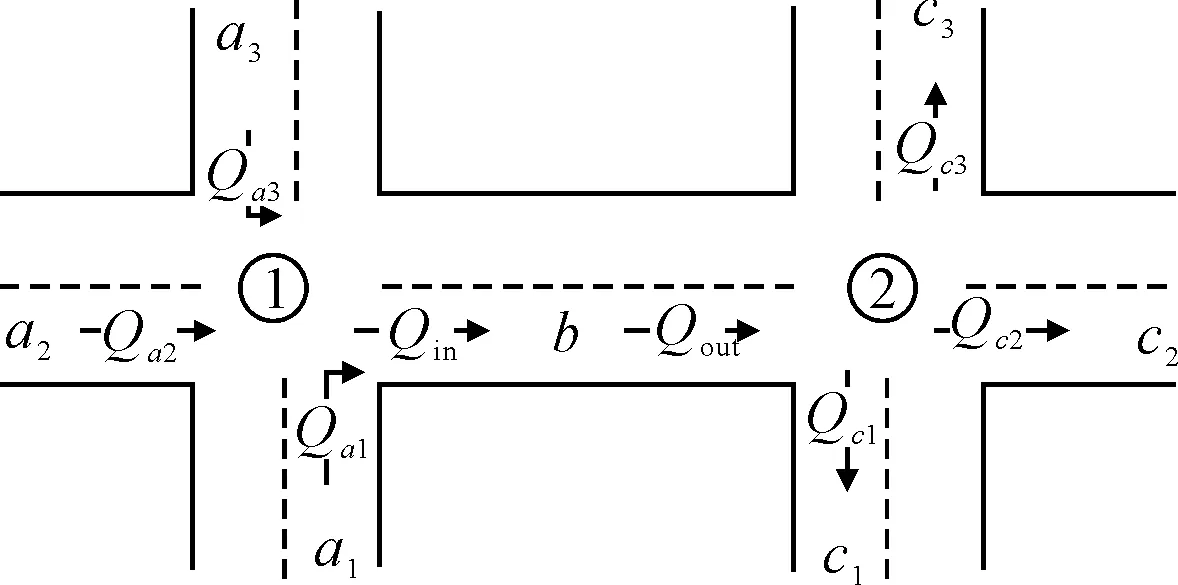
图5 路段数据信息
4.2 路段分层结构
瓶颈被识别后,匹配车牌,按照式(1)~(2)计算上、下游路段和瓶颈路段的关联度,并根据瓶颈位置和路段之间的连接关系进分层.瓶颈路段为第0层,与之直接相连的上游或下游路段为第一层,依次类推.每一层的分支总数为上一层的路段总数.存储完成后得到两个树形结构,一个上游,一个下游,见图6.

图6 路段分层结构
在上游分层过程中标记每条路段的瓶颈相关转向.上游路段相关转向是指通过此转向驶离上游路段的车辆最终会进入瓶颈路段.因路网的结构特点,一条路段可能会同时出现在不同层,同时有不止一个转向是瓶颈相关转向,此时只记录其第一次出现的位置和转向.在下游分层过程中,每条路段同样只记录一次,但因所有转向都是相关转向,所以不需要对此进行标记.下游路段相关转向是指从瓶颈路段驶出的车辆最终会经过该转向驶离下游路段.
图7为相关转向关系,相关以上游为例,图7中路段编号A-B,A为路段所在层级,B为路段在其层级中的序号.1-1即为1层1号路段.在图中路段1-1的相关转向为左转,1-2的相关转向为直行,1-3的相关转向为右转.

图7 相关转向关系
4.3 基于分层结构修正关联度
关联度通过过车记录匹配得到,过车记录中包含真实的记录和补全的记录.由真实记录计算出的关联度记为δ,由补全的记录计算出的关联度记为δ′.通过路段分层结构可以知道,父路段的关联度等于其所有子路段关联度的和.图8为路段关联度示意图,对路段a2有:
δa2=δa4+δa5+δa6
(7)
δa2=δa0-δa1-δa3
(8)

图8 路段关联度示意图
因此可以流量修正的原理,对δ′进行修正.
4.4 基于分层结构补全缺失关联度
在某路段关联度缺失,但其上下游关联度完整的情况下,可以根据路段分层结构用已知关联度(包括真实关联度和对补全数据修正后的关联度),根据式(7)~(8)推导出缺失关联度.
关联度修正和补全步骤见图9.
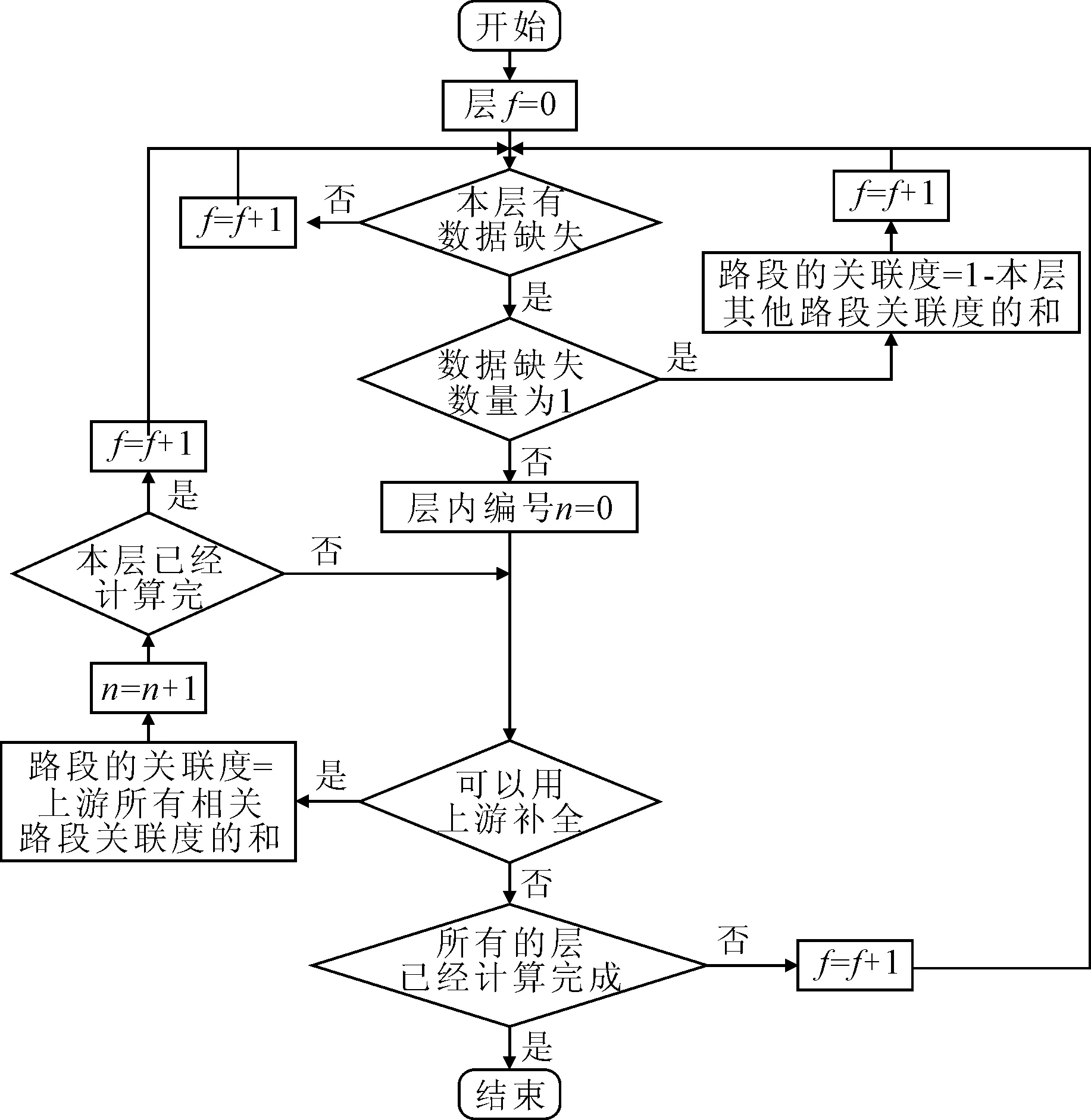
图9 用已知关联度补全未知关联度
4.5 用流量数据修正填补后的关联度
4.5.1上游路段关系及关联度推导
父路段和子路段同属一个交叉口,父路段为交叉口的出口路段,子路段为流量可能流入父路段的交叉口入口路段.若父路段属于第f层,那么子路段属于第f+1层.图10为上游路段关系示意图,路段a1为父路段,路段a2,a3,a4为子路段.

图10 上游路段关系示意图
设a为瓶颈路段的上游路段(子路段);b为瓶颈路段(父路段);qb,in为瓶颈路段流入流量;qa,out,i为路段a出口转向i的流量.按照路段存储结构,从第一层开始,计算关联度δa,1:
(9)
更一般地,从第二层开始路段关联度为
(10)
依次递推.从第二层开始,路段的关联度可以由本路段出口相关转向的流量,父路段出口总流量,父路段关联度,三个参数计算得到.
4.5.2下游路段关系及关联度推导
父路段和子路段同属一个交叉口,父路段为交叉口的进口路段,子路段为从父路段出来的车辆可能驶向的交叉口出口路段.若父路段属于第f层,那么子路段属于第f+1层.图11为下游路段关系示意图,a1为父路段,a2,a3,a4为子路段.
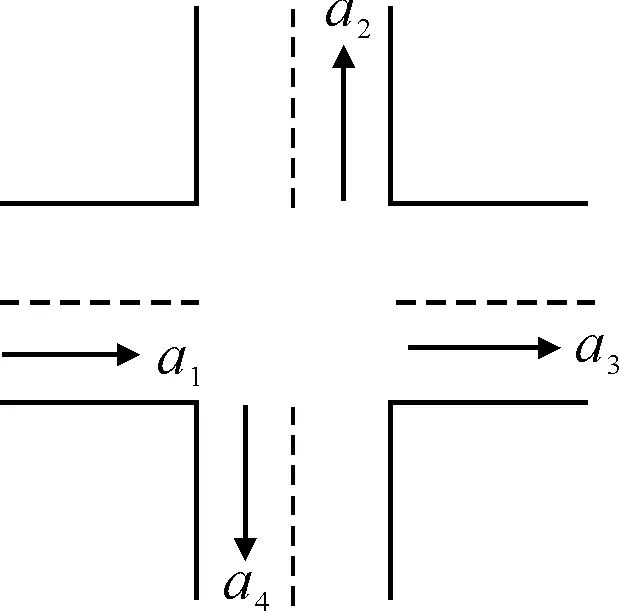
图11 下游路段关系示意图
设c为下游路段,b为瓶颈路段,qb,out为瓶颈路段流出流量,qc,in,i为路段入口转向i的流量.按照路段存储结构,从第一层开始,计算关联度δc,i:
(11)
从第二层开始路段关联度:
(12)
从第二层开始,路段的关联度可以由父路段出口相关转向的流量,父路段出口总流量,父路段关联度,三个参数计算得到.
在4.5.1和4.5.2中,需要用父路段关联度计算当前路段关联度,经过多层累积会存在误差增大的情况,因此可用4.3节中可信度较高的关联度来替换父路段的关联度,以减小累积误差.在所有路段的关联度计算完成后,与4.3,4.4计算得到关联度进行对比.若根据4.5未给出关联度值,以4.4计算结果为准;若4.3与4.4均给出计算结果,用它们的均值作为关联度的最终结果.
5 算例分析
采用浙江省某市的路网数据结合VISSIM交通仿真软件进行算法验证.路网包含57个交叉口,其中信号控制交叉口34个,无信号控制交叉口23个.有过车记录的交叉口26个,无过车记录的交叉口31个.图12为路网卫星图,图13为路网简化的拓扑图,有编号的交叉口为信号控制交叉口,黑色圆点覆盖的交叉口为有过车记录的交叉口,圆点上的数字为交叉口编号.

图12 路网卫星图
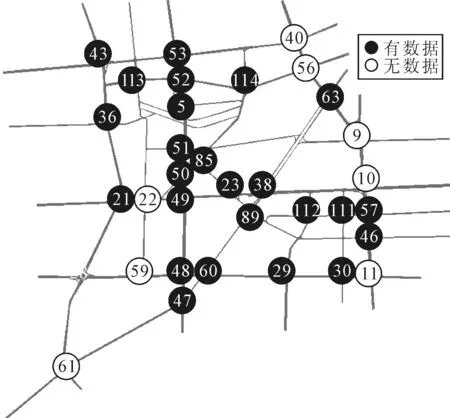
图13 路网数据覆盖情况
在算法运行前,建立基础数据表tb_cross存储路口信息,见表4.tb_road存储路段信息,见表2.tb_lane存储车道信息,见表5.

表4 路口信息

表5 车道信息
算法每5 min运行一次,读取30 min之前到当前时刻的所有过车记录,进行过车数据填补和流量填补,并把计算结果写入数据库.在49号交叉口西向东的路段被识别为瓶颈路段后,开始进行路段分层.上、下游分层结果见图14.其中箭头方向表示车流方向,数字表示路段在分层结构中所在层级.瓶颈路段为第0层,与之直接相连的路段为第1层,依次类推.因路网较大只展示到第3层.

图14 上、下游路段分层
以上游为例,分层结构见图15.

图15 上游路段关系
其中路段与路口的关系见表6.
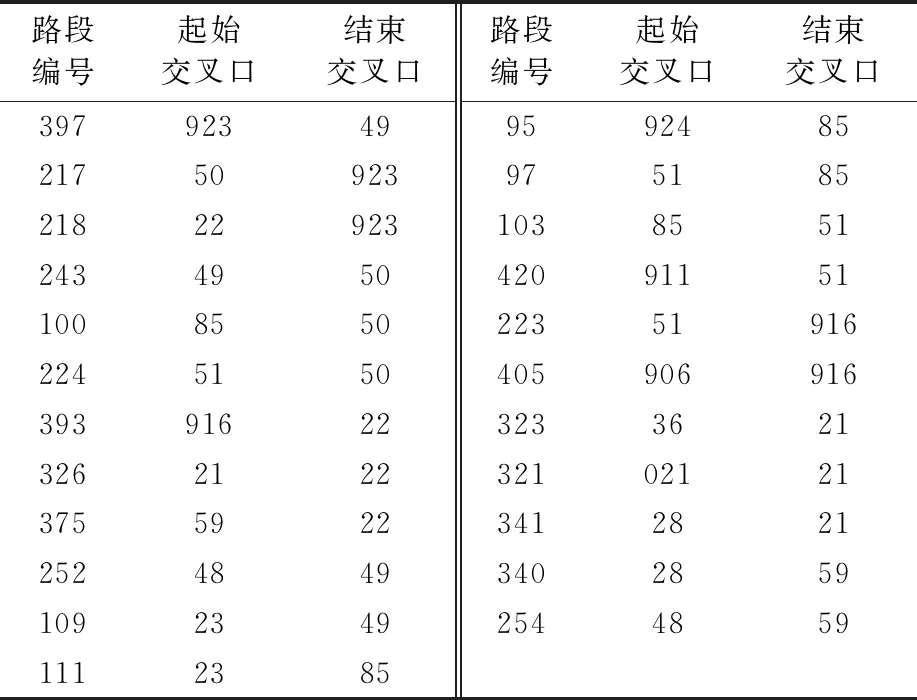
表6 路段与路口关系
为验证数据补算法的有效性,做两组实验进行对比.第一组实验为在仿真条件下,没有数据缺失,所有交叉口均能采集到数据,直接计算出各个路段与瓶颈路段的关联度.第二组实验在仿真条件下,有数据缺失,不采集无信号控制交叉口的数据,利用数据补全算法补全缺失关联度.下面将第一组的结果称为真实值,将第二组的结果称为计算值.数据结果见图16,结果对比见表7.
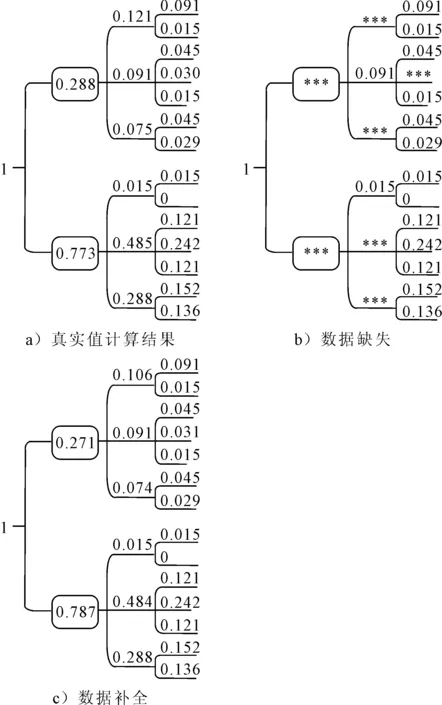
图16 数据结果

表7 结果对比
由表7可知,数据补全算法能够有效地对缺失关联度进行补全.
6 结 束 语
为分析瓶颈路段流量的来源和去向,考虑到实际应用中交叉口视频检测设备存在覆盖率低、错检、漏检等情况,导致数据缺失,提出了一种过车记录缺失下的路段关联度计算方法.通过过车记录补全,流量补全和修正,最终达到关联度补全和修正的目的.算例分析表明,补全算法能够有效地提高数据完整性.
