热-水-力作用下混凝土细观XFEM全耦合建模*

徐 政 夏晓舟 章 青

(河海大学力学与材料学院 南京 211100)

0 引 言

水工、道路混凝土结构由于使用环境的特殊性，发生的破坏往往是力荷载、温度荷载与渗流荷载共同作用的结果[1].混凝土材料多场耦合机制与数值方法的研究被广泛关注[2-3]，Tobias等[4]使用耦合分析的方法预测混凝土结构的长期变形，Koniorczyk等[5]把混凝土看作均质材料研究了热-水-力三场耦合作用下的冻融损伤.陈德鹏[6]利用湿膨胀系数进行了隧道混凝土的湿-热-力三场耦合数值模拟.Gong等[7]探究了钢筋混凝土构件在热-水-力耦合下的非均匀性.但是Powers[8]认为骨料与砂浆的热膨胀系数差异很大，必须将骨料与砂浆分开考虑，即必须在细观层面建模才能真实的反映混凝土在湿热环境下的力学行为；因此，Zhou等[9]在细观层次下探讨了材料参数对混凝土多场耦合力学行为的影响机制.上述学者均采用有限元方法进行数值模拟，Gong等[10]使用了刚体弹簧元方法，但弹簧刚度难以准确给出.扩展有限元[11-12]在处理夹杂问题时，网格划分不依赖于骨料边界，更适合混凝土细观数值模拟.

为了探究混凝土材料在湿热环境下的力学行为，避开有限元复杂的网格剖分，文中将在扩展有限元的框架下，把砂浆视为基体材料，骨料视为夹杂相，进行混凝土在热-水-力作用下的全耦合数值建模.即利用单位分解的思想，在有限元形函数的基础上引入阶跃附加形函数反映骨料界面处的相对位移，引入距离附加函数反映骨料界面处渗流压力和温度的弱连续性，由运动方程、连续性方程及热量平衡方程，通过它们的积分弱形式，由散度定理建立混凝土在热-水-力作用下的扩展有限元全耦合模型，并应用建立的模型来模拟混凝土内部基体和骨料上的应力、温度、热流、渗透压力及渗流的分布规律，探究冷缩时骨料级配对温度应力的影响机制.

1 扩展有限元热-水-力耦合建模

1.1 基本方程及定解条件

假设混凝土内部流体与骨架之间没有相对加速度，则固-液混合物的运动方程可表示为

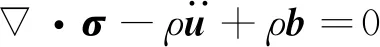
(1)

假设固-液混合物为均匀的各向同性体，得到混合物的连续性方程[13]：

α·vs+·[kf(-p+ρfb)]+

(2)

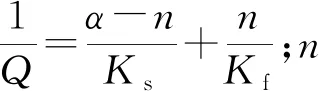
假定混凝土内部渗流满足达西定律，忽略固相速度，由任意固定体积上的热量平衡原理[14]，可导出热传导控制方程为

(3)

式中：(ρC)avg=(1-n)(ρC)s+n(ρC)f，其中c为热容；κ为导热系数矩阵，定义为κ=(1-n)κs+nκf，左边第二项为流体流动对传热的影响项.

混凝土受热-水-力耦合作用的边界条件见图1.其中变形场的边界条件为

(4)

式中：nΓ为外部边界Γ的单位外法向量.渗流场的边界条件为

(5)

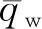
图1 边界条件

1.2 积分弱形式

对于位移场、渗流场和温度场分别取试函数δu，δp，δT，结合图1边界条件，由散度定理，获得方程(1)～(3)的积分弱形式分别为

(6)

(7)

(8)

1.3 位移、渗压及温度的插值模式

界面过渡区具有一定的厚度，通过引入厚度参数，把界面过渡区看作无厚度的构型，因此界面过渡区的位移分布可通过骨料界面处的相对位移表达，即在无厚度构型上考虑界面处的位移不连续，由此，对于含界面过渡区的扩展有限元，其位移模式取为

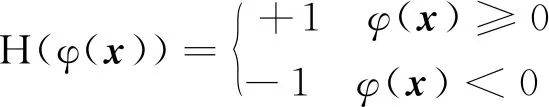
(10)

对于渗流场，渗压在界面处是弱不连续的，即渗压场连续，而其垂直于界面的渗压梯度在界面处是不连续的，由此，单元中渗压可定义为

(11)

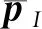
(12)

温度场的插值模式与渗流场类似，定义为

(13)

1.4 热-水-力三场的区域离散化

基于Bubnov-Galerkin法将积分弱形式方程进行区域离散，得

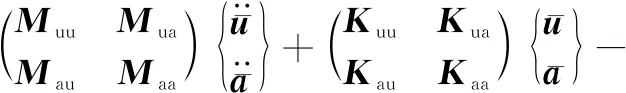
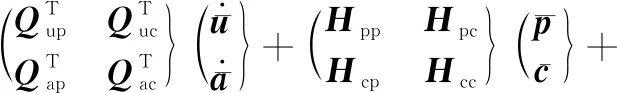
(14)

式中：M为质量矩阵；K为刚度矩阵；Q为流-固耦合矩阵；W为热-力耦合矩阵；H为渗透矩阵；S为压缩矩阵；R为热-流耦合矩阵；L为热容矩阵；C为热传导矩阵；fext，qext和gext为外力矢量，各矩阵和矢量定义为(α,δ,λ分别为标准结点，β,γ,κ分别为加强结点)：

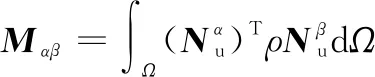
(15)

1.5 时间离散化

对时间进行离散，由当前步的结果，通过纽马克时域积分，获得下一时刻的加速度、速度和位移，渗压变化率和渗压，以及温度变化率和温度为

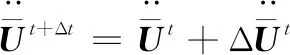
(16)

(17)

从而得到热-水-力全耦合的非线性扩展有限元迭代格式为

(18)

式中右端项:

(19)

1.6 单元积分方案

在进行混凝土细观尺度的扩展有限元建模过程中，会出现同一单元包含砂浆与骨料这两种完全不同力学性能材料的情况.对于这种单元可按材料区域进行三角形子划分[15]，从而保证单元刚度矩阵计算的准确性，见图2.

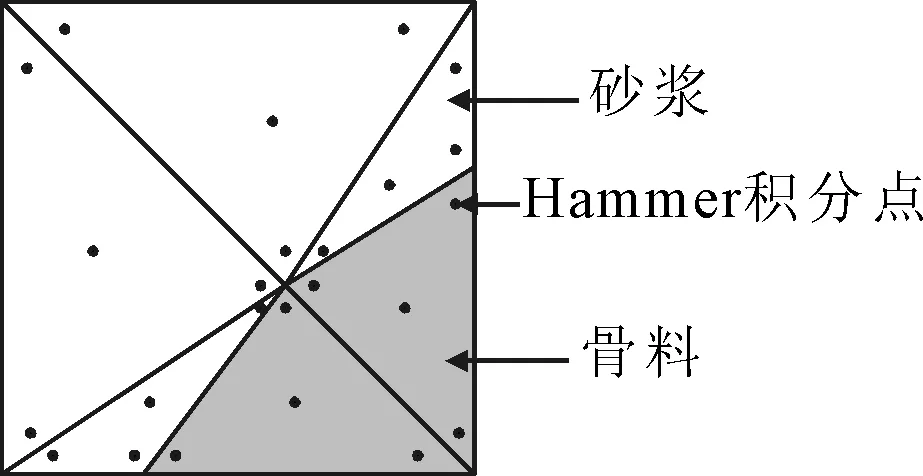
图2 扩展单元的子域积分方案

2 数值算例

2.1 可靠性验证

为了验证文中建立的热-水-力全耦合扩展有限元模型的可靠性，将其计算结果与热-水-力耦合有限元计算结果进行对比.所选算例见图3，在平面应力条件下模拟150 mm×150 mm的正方形板，其中心位置处存在一个夹杂.算例中初始温度场为0 ℃，底部为流量入口边界，q=10-6m/s，温度固定为20 ℃；顶部作为排水边界条件，固定为零的压力值和温度值.左右两边水平方向位移固定为0，底部竖直方向位移固定为0，取AB路径作为考察断面.

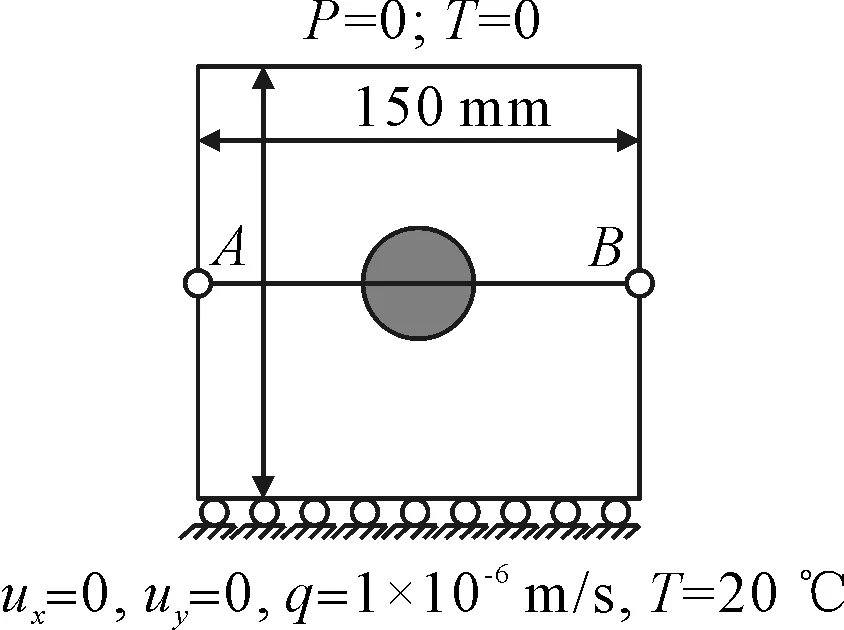
图3 边界条件

图4比较了两种方法的计算结果，d为到A点的距离.整体随温度上升有膨胀趋势，受底部边界条件等约束不能自由移动产生温度应力[16-17]，其中因为两种材料热胀系数不同，应力x分量在交界处最大，而y分量在交界处最小，扩展有限元计算结果与有限元结果较为吻合.

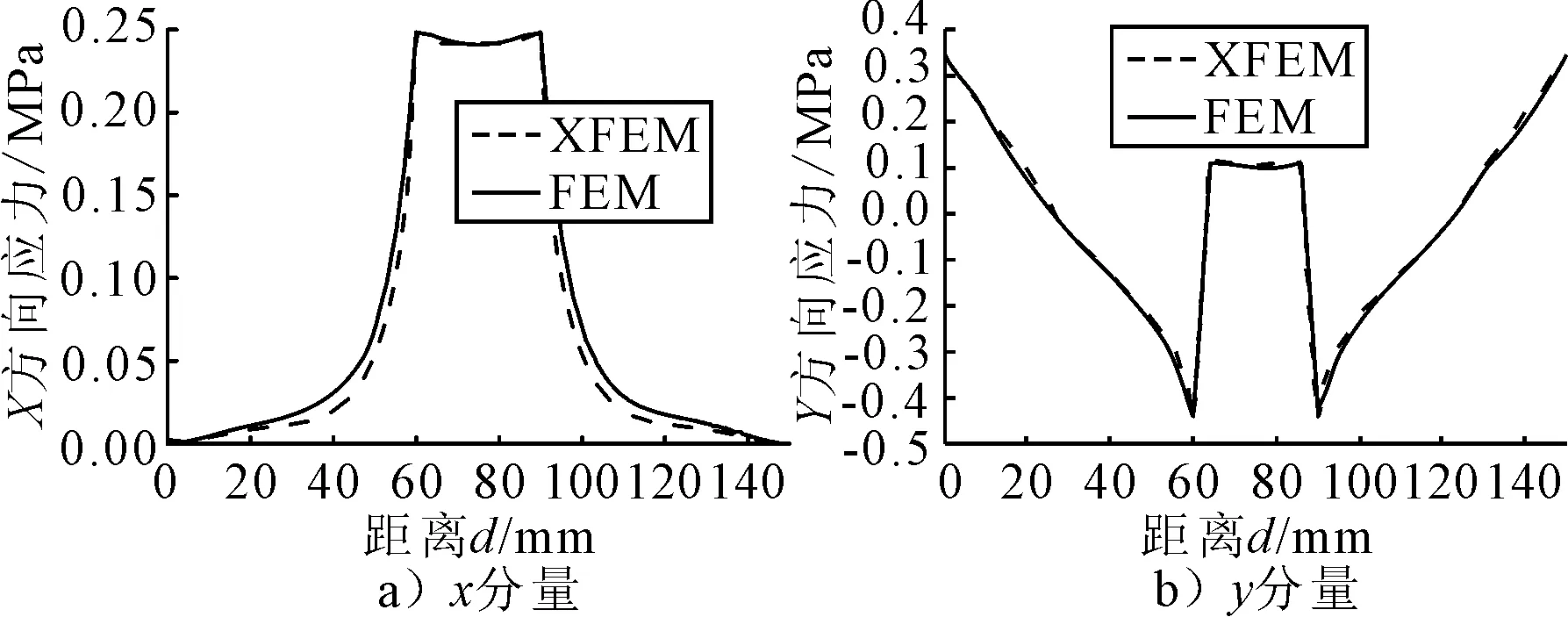
图4 应力x和y分量沿AB路径的分布

图5为渗流速度和热流密度y向分量和沿AB路径的分布.由于在底面施加了流体流量，整个区域内的孔隙水压力增大，由于夹杂的渗透性更低，所以法向渗流速度比基体处更低，约为渗流边界条件值的1/5，在两种材料交界处渗流速度值最大，比入口边界值大80%；由图5b)可知，底部的热量向上传导过程中，夹杂的导热系数更大导致夹杂内部的热流密度更大，在交界面处热流密度值最低.两种方法的计算结果与分布规律较为一致，这证明了扩展有限元模型在处理含夹杂热-水-力全耦合问题时的合理性与可靠性.

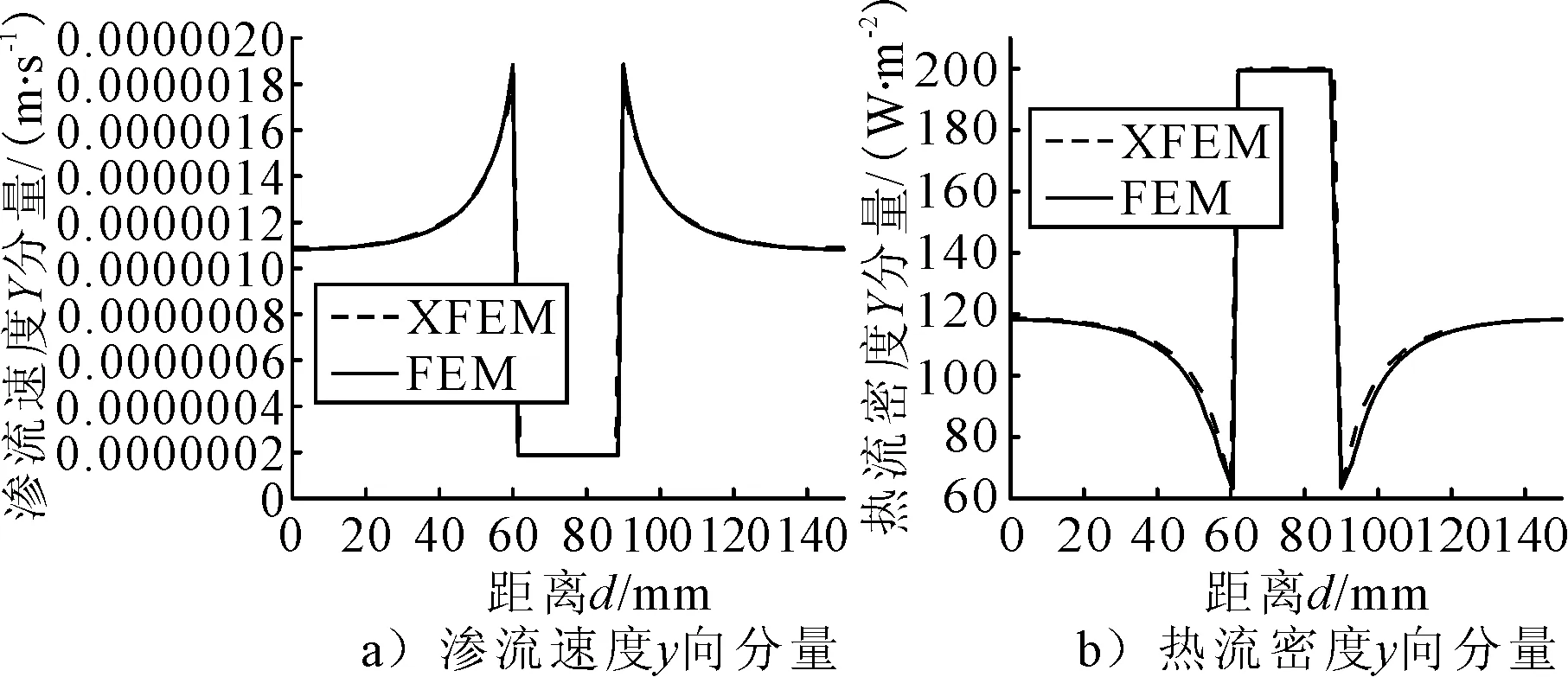
图5 渗流速度和热流密度y向分量沿AB路径的分布

2.2 混凝土细观尺度模拟

随机生成椭圆骨料的混凝土试件，试件尺寸为150 mm×150 mm，其骨料体积分数为30%.将砂浆和骨料的参数应用到混凝土细观尺度的热-水-力全耦合分析中，物性参数见表1.

试件的温度初始条件为20 ℃.底部为流量入口，q=10-6m/s，底部位移固定为0，温度为20 ℃；顶部作为排水边界条件，温度固定0 ℃不变.

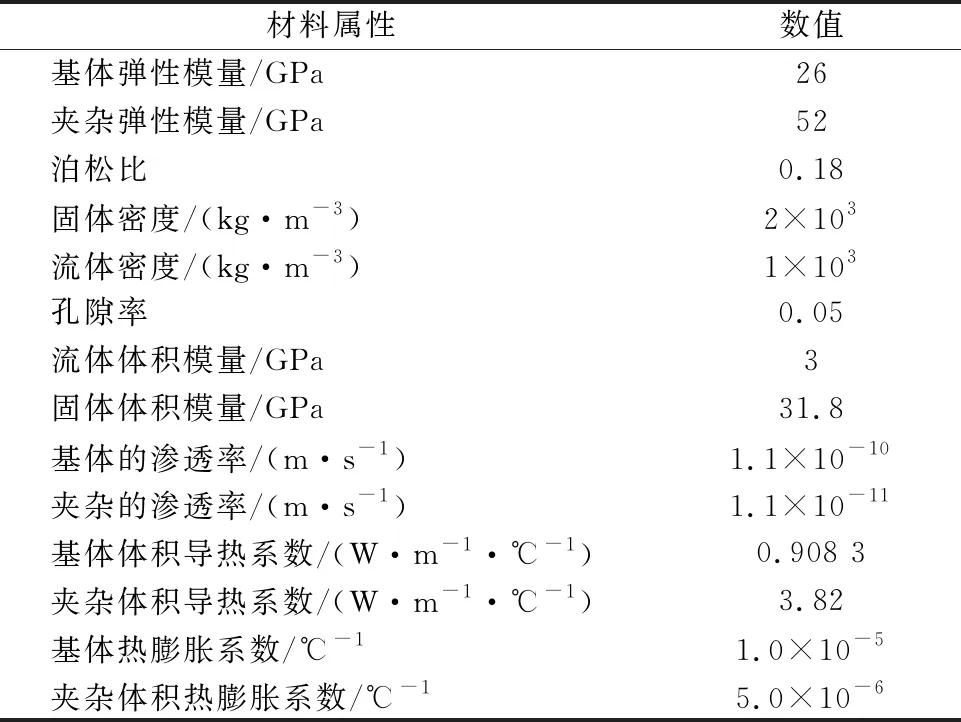
表1 算例材料参数

温度的下降导致试件整体有收缩趋势，底部的位移约束阻止了收缩，砂浆整体产生拉应力，不同材料降温产生的热应变差异导致拉应力在界面过渡区更大，见图6.最大主应力出现在骨料与砂浆界面区，倘若最大拉应力值超过界面抗拉强度则混凝土会发生收缩开裂的现象[18]，界面过渡区附近为易发生破坏的薄弱区.

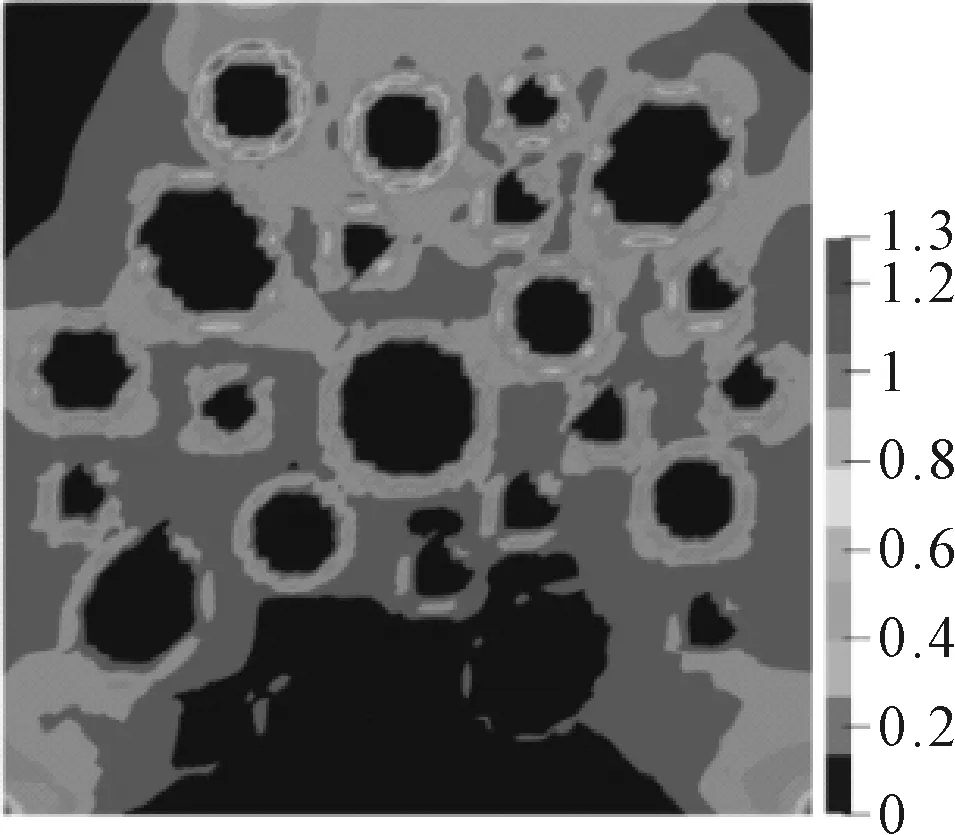
图6 第一主应力分布(单位：MPa)

模拟结果表明混凝土中的孔隙水压力在骨料和砂浆界面处有明显的不连续，温度的分布也受到骨料存在的影响，均沿骨料边界层状分布.热流密度因骨料导热系数较大，在骨料竖向连接之间较大.渗流速度法向分量反映出由于骨料渗透系数较小，故在骨料处较小，在垂直于渗流方向的界面过渡区达到最大值，为入口边界条件的3倍左右，这可能导致在界面处强度下降甚至引起混凝土沿骨料砂浆界面发生层状破坏.

在试件中取A，B两点作为具体研究对象，A,B点温度差见图7.由图7可知，在模拟刚开始的25 min内，A,B两点间的温度差迅速增长达到最大值0.56 ℃左右，这种迅速扩大的温差是由温度梯度较大造成.此后由于底部施加的温度，试件整体温度分布趋于均匀，两点间的温度差逐渐下降，在2 h后逐渐平稳.可见混凝土受冻融等热-水-力耦合作用时，在环境温度发生变化的初期，骨料砂浆温度分布更不均匀.

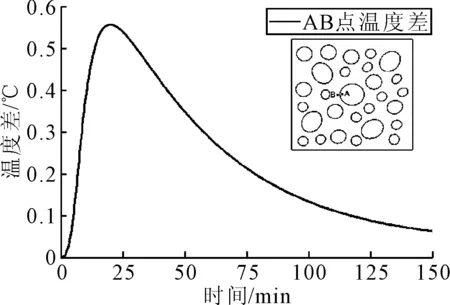
图7 AB点温度差

为了研究不同骨料粒径与分布的影响，分别随机生成骨料体积分数30%的一、二、三级配混凝土试件见图8.通过分析不同级配混凝土试件受渗流荷载、温度荷载作用时，产生的最大第一主应力可以发现，骨料粒径越大，产生的第一主应力越大，故在考虑设计混凝土材料时，不宜使用过大粒径的粗骨料，这与实验结果相一致.

图8 最大第一主应力

3 结 论

1) 扩展有限元法网格具有独立于物理边界的特性，结果表明用结构化的网格也能准确反映出混凝土中孔隙水压力和温度在骨料砂浆界面处的不连续，在三维网格剖分困难的情况下模拟混凝土受多场耦合作用时，扩展有限元法有着特殊优势和巨大潜力.

2) 分析热-水-力耦合作用下的温度场、应力场和渗流场发现，骨料砂浆的界面过渡区及其周围区域在热-水-力耦合作用时容易成为薄弱区.

3) 在热-水-力耦合作用的初期，骨料砂浆间温差更大.混凝土的级配也对其在热-水-力耦合作用下的性能有影响，模拟的降温过程中三级配混凝土产生的第一主应力比一、二级配混凝土更大，在混凝土级配设计时应避免使用过大粒径的粗骨料.