认知无线电网络中的非正交多址资源分配算法
2019-12-26贾亦真姚枝秀周梦圆
贾亦真,姚枝秀,周梦圆,熊 炜
(1.军事科学院 系统工程研究院,北京 100000;2.重庆邮电大学 重庆市移动通信技术重点实验室,重庆 400065;3.重庆市住房公积金管理中心,重庆 401121)
0 引 言
目前人们对数据速率需求呈指数型增长,迫切需要大量的频谱资源。然而,频谱资源是非常紧缺的,根据当前频谱政策,大部分可用频谱已经分配或许可给无线服务提供商,如蜂窝公司、电视、广播电台和卫星通信。据美国联邦通信委员会调查,大量许可频谱的平均使用率为15%至85%[1]。为了解决频谱稀缺性问题,认知无线电技术成为解决该问题的关键,该技术通过允许未被授权用户,即次用户(secondary users, SUs)接入已授权用户,即主用户(primary users, PUs)未占用的频谱,同时保证主用户的服务质量,从而提升次用户的频谱效率[2]。
在传统认知无线电网络中多采用正交多址技术进行用户复用,而大量文献已经证明非正交多址接入技术频谱利用率优于正交接入技术,因此,目前如何将非正交多址接入(non-orthogonal multiple access, NOMA)技术和认知无线电结合,成为新的研究热点。NOMA与认知无线电技术的结合,更能体现出NOMA技术的优势[3]。文献[4]提出了一种2用户信道分配算法,在该算法中,最佳子信道分配策略是子信道始终选择在该子信道上具有最强等效信道增益的用户进行匹配。文献[5]提出一种多用户信道分配算法,在该算法中,子信道倾向于选择使其能效最大的用户集合与该子信道进行匹配。文献[4-5]中,子信道均是以最大化子信道效益为准则挑选用户,因此,以上2种策略非常容易促使信道状态信息相近的用户复用到同一子信道上。而这种情况会影响接收端的正确解调性能,且会造成用户间公平性的降低[6],这是由于系统是按照复用用户的信道增益情况进行功率分配,因此,每个复用用户所分配的功率差值较小,用户间的干扰增大。文献[7-8]考虑了基于比例公平调度的信道分配问题,其中,每个子信道上的多用户调度和功率分配结果,都可以通过最大化小区内所有用户的平均用户吞吐量乘积来获得。文献[9]研究了在认知无线电NOMA网络下行链路信道分配问题,提出了一种基于一对一匹配模型的信道分配算法,在该系统中,一个主用户和一个次用户以NOMA的方式进行复用。
文献[10-13]研究了基于稳定匹配理论的信道分配问题。文献[10]分析了上行链路认知毫微微蜂窝网络的最大化吞吐量问题,并提出了一种基于匹配理论的分布式算法。文献[11]考虑了最大化主用户和次用户效用函数问题,并提出了一种基于匹配理论的分布式用户匹配算法。文献[12]提出了一种新的基于蚁群的信道分配算法以提高系统吞吐量和系统公平性。文献[13]提出了一种基于定价的的信道分配算法。在该算法中,每个非合作的用户都是自私的,只根据自己的收入来选择供应商,供应商根据收入最大化的原则对频谱进行定价。
除了频谱效率,能效也是5G中的关键性能指标之一。在NOMA系统的能效优化方面,文献[14]研究了NOMA异构网络下行链路的子信道分配和功率分配问题以最大化系统能效。文献[15]利用李亚普诺夫优化模型方法,提出了在NOMA网络中同时考虑最小用户服务质量和最大发射功率限制的能效优化信道分配和功率分配策略。文献[16]研究了在每个子信道最多可复用2用户的情况下,讨论了NOMA系统能量效率最大化问题。
虽然上述研究工作对传统认知无线电网络中的非正交多址信道分配和功率分配算法进行了充分研究,但依然未能解决信道状态信息相近的用户复用到同一子信道上的问题。本文针对认知无线电网络中的非正交多址技术,综合考虑信道和功率资源,以最大化次用户网络能效。此外,为了降低算法复杂度和避免信道状况相近的用户复用在同一子信道,提出了一种次优公平性可调的信道分配算法。由于功率分配问题为非线性分式规划问题,本文采用连续凸近似、变量替换和Dinkelbach算法迭代求解最优能效值。仿真结果表明,所提算法可以显著提升系统能效。
1 系统模型与问题建模
1.1 系统模型
图1为认知无线电网络中的NOMA下行链路模型。在该网络中次用户以频谱共享模式接入PUs授权的频谱。次用户基站以单天线的方式通过M个主用户已授权的子信道传输N个次用户信号。将i记作次用户SUi的索引,定义n={1,2,…,N}表示次用户的集合。将m记作主用户PUm的索引,定义m={1,2,…,M}表示主用户的集合。为了便于分析,主用户PUm所授权的子信道也记作m,即子信道m。同时,假设有L个次用户以NOMA的方式复用在子信道m上,其中,L≤Lmax≤N,Lmax为子信道m允许的最大接入用户数,则子信道m上,次用户基站发送的信号为
(1)
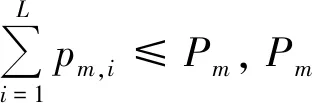

图1 下行链路系统模型
因此,在理想信道条件下,次用户SUi接收到的信号为
(2)
(2)式中:Gm,i为子信道m上次用户基站到次用户SUi的信道增益;hi为主用户基站到次用户SUi的信道增益;pp为主用户基站发送主用户PUm信号的功率;xp为主用户基站发送的PUm信号;nm,i为次用户SUi在接收端均值为0,方差为σ2的高斯白噪声。在本文中将接收端噪声与来自主用户PUm的干扰功率定义为Nm,i,可以表示为Nm,i=σ2+|hi|2·pp,∀i∈L。因此,在经过完美串行干扰消除(successive interference cancellation,SIC)之后,用户SUi接收到的信号与干扰加噪声比 (signal to interference plus noise ratio,SINR)为
(3)
(3)式中,Hm,i=Gm,i/Nm,i,表示用户SUi在子信道m上的等效信道增益。根据香农公式,子信道m上所有复用用户的吞吐量为
(4)
(4)式中:Rm,i表示是在子信道m上次用户SUi的吞吐量;Bm为子信道带宽。因此,系统总吞吐量可以表示为
(5)
为了保证次用户的服务质量,每个次用户都需要满足一个最小速率,定义最小速率为Rmin,因此,次用户SUi的速率约束为
Rm,i≥Rmin,∀m∈M
(6)
相对应的最小功率值为
(7)
本文中,次用户在采取频谱共享接入模式占用主用户PUm的频带时,也对PUm的通信造成了一定的干扰,因此,需要保障PUm的通信质量。故次用户基站分配给子信道m的功率应该限制为
(8)
(8)式中:gm为次用户基站到主用户PUm的信道增益。
1.2 问题建模
在本小节中,建立认知无线电网络中的NOMA能效优化资源分配问题。系统能效定义为系统总速率与总消耗功率之比。因此,系统能效表示为
(9)

(10)
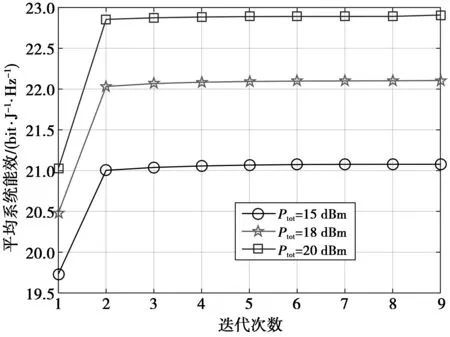
(10)式中:约束条件C1表示基站总功率约束;约束条件C2表示每个次用户SUi达到的最小速率约束;约束条件C3表示每个主用户PUm可忍受的干扰功率约束;约束条件C5表示一个次用户最多复用一个子信道;约束条件C6表示一个子信道最多允许复用的用户个数。由于约束条件C4的存在,所以问题(10)是一个混合整数非线性分式规划问题,因此,很难在多项式时间内获得问题最优解。为了使该问题比较容易被解决,所以将原始优化问题分解成2个问题,信道分配问题和功率分配问题,并进行逐一求解。
2 能效资源分配算法
2.1 次优化公平性可调的信道分配算法
考虑第1节中提到的情况,在文献[4-5]的基础上,本节提出了一种公平性可调的信道分配算法。该算法的主要思想是将用户分配到不同的子信道,同时避免信道状态信息相近的用户复用到同一子信道内,以提高用户的公平性和降低接收端的误码概率。由于问题(10)的约束条件C5和C6的限制,所以最多有dmax个用户复用在相同子信道,且一个用户最多只被允许接入一个子信道。在所提算法开始时,假设基站在所有次用户之间进行均等功率分配,即pm,i=Ptot/N,其中,Ptot为次用户基站总功率。所提算法具体描述如下。
步骤1基于用户的子信道信息,构建等效信道增益矩阵H=|Hm,n|M×N。
步骤2初始化Uun为尚未分配到任意一个子信道的用户集,Uun={1,2,…,N};Hmatch(m)为记录复用到子信道m的用户集,Hmatch(m)为空集。
步骤3每一个n∈Uun选择使其等效信道增益最大的子信道m*,表示为
(11)
(11)式中,Hn表示矩阵H的第n列元素。
步骤4如果复用在子信道m*上的用户数小于dmax,则将用户n分配到该子信道,并更新Uun,即将用户n从Uun中删除;反之,则进行步骤5。
步骤5如果复用在子信道m*上的用户数等于dmax,则从用户集{Hmatch(m*),n}选择使子信道调度准则最大的用户集Uaccept,并拒绝未被选中的用户Ureject。子信道调度准则为
SCm*,utility=
(12)

步骤6更新列表Uun。从Uun中删除被接受的用户,并添加被拒绝的用户。
步骤7更新矩阵H,将被拒绝的用户Ureject所在列的第m*行置零。
步骤8检查Uun是否为空集,若为空集,则终止算法;否则,返回步骤3。
算法1给出了本小节设计的次优公平性可调的信道分配详细求解过程。
算法1次优公平性可调的信道分配算法。
1:构建等效信道增益矩阵H=|Hm,n|MN;
2:初始化Uun为尚未分配到任意一个子信道的用户集,Uun={1,2,…,N};Hmatch(m)为复用到子信道m的用户集,Hmatch(m)=∅;
3:whileUun≠∅ do

5: If |Hmatch(m*)| 6: 将用户n分配到该子信道m*上; 7: 更新集合Uun,Uun←Uun
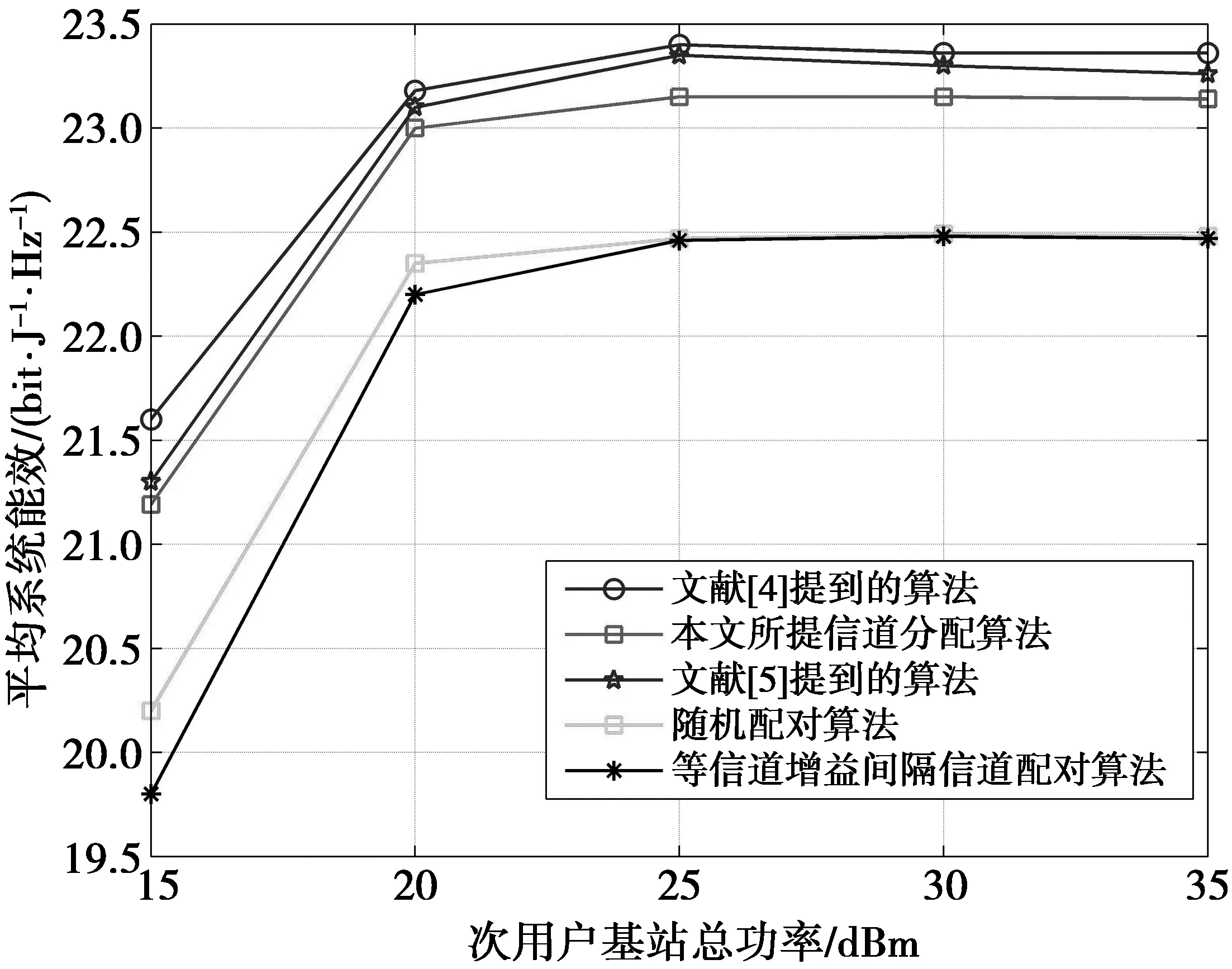
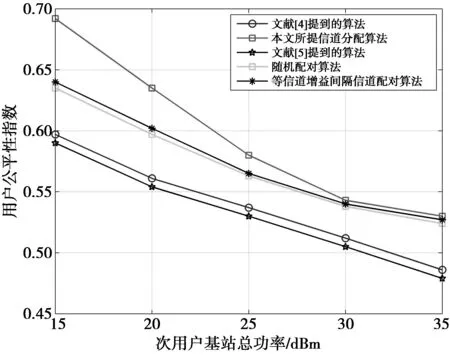
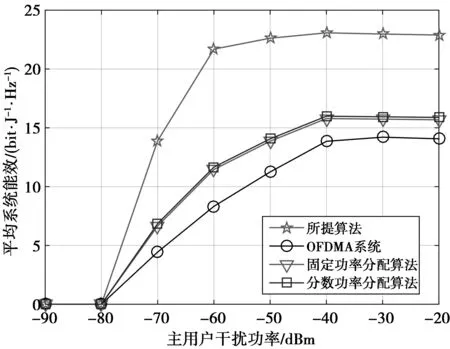
; 8: else 9: 从用户集{Hmatch(m*),n}选择使子信道的调度准则最大的用户集Uaccept,且|Uaccept|=dmax; 10:子信道m*拒绝未被选中的用户Ureject; 11:更新集合Uun。将被接受的用户从Uun中删除,Uun←UunUaccept;将被拒绝的用户加入列表,Uun←Uun∪Ureject; 12:更新等效信道增益矩阵H,令第m*行第Ureject列元素置零; 13: end if 14: end while 在信道分配算法完成之后,为了进一步提升系统能效,基站需要为子信道内的复用用户分配合适的功率值。在满足问题(10)的功率约束条件下,基站需要确定同一子信道内不同次用户之间的最佳功率值。为了计算简单,假设认知无线电基站在子信道之间进行均等功率分配。对于给定的用户分配算法结果,根据问题(10),子信道内功率分配问题可以写为 (13) (14) (15) 因此,问题(13)的目标函数下界可以写为 (16) 同理,约束条件C2可以写为 (17) 在(17)式不等式两边进行对数操作后,此时可以看作是一个凸集 (18) 因此,能效优化功率分配问题可以进一步表示为 (19) 定理1问题(19)的目标函数分子部分为凹函数,分母部分为凸函数。 证明问题(19)的目标函数可以写为 (20) 由于g(qm,i)关于qm,i的二阶偏导数大于零,即2g(qm,i)=(ln2)22qm,i>0,所以,g(qm,i)是关于qm,i的凸函数。而f(qm,i)可以写为 f(qm,i)= (21) (22) 由于h1(qm,j)为指数和的对数函数,而指数和的对数函数为凸函数,因此,h1(qm,j)为凸函数。根据凸优化理论可知,-h1(qm,j)为凹函数。因此,(21)式的第2项为凹函数。故f(qm,i)为凹函数。到此得证,问题(19)的目标函数分子部分为凹函数,分母部分为凸函数。 Dinkelbach算法的核心思想是将分式形式等效转化为含参数t的减法形式。因此,问题(19)可以等效写为 s.t.C1,C2,C3 (23) (24) (24)式中,λ,μ和ν分别为拉格朗日乘子。则对于给定的t,(24)式可以重新写为 (25) (25)式中, (26) 因此,对于给定的t,问题(23)的对偶问题可以写为 s.t.λ≥0,μ≥0,ν≥0,q≥0 (27) (28) 算法2给出了问题(27)的详细求解过程。在算法2的迭代过程中,拉格朗日乘子将按照下列公式进行更新。 (29) (30) (31) (29)—(31)式中:[x]+=max{0,x};k是迭代索引;s1(k),s2(k)和s3(k)是每次迭代中的步长。算法2的详细步骤如下。 算法2可迭代功率分配算法。 1:初始化外层迭代索引n,外层最大迭代次数Nmax,外层容忍误差ε; 2: whileF(tn)≥εorn≤Nmaxdo 3:初始化内层迭代索引k,内层最大迭代次数Kmax,内层容忍误差ζ; 4: while |λ(k+1)-λ(k)|+|μ(k+1)-μ(k)| +|ν(k+1)-ν(k)|≥ζork≤Kmaxdo 5: form=1:Mdo 6: fori=1:Ldo 8: 根据式(28)计算qm,i(k); 9: 计算p(k)=2q(k); 10: 根据(29)—(31)式更新拉格朗日乘子λ,μ和ν; 11: end for 12: end for 13: end while 16:n=n+1; 17: end while 图2 不同基站发射功率下算法的迭代收敛过程 图3描述了不同信道分配算法情况下,平均系统能效与次用户基站总功率的关系。在仿真过程中,采用随机配对算法[18]、等信道增益间隔信道分配算法[19]以及文献[4-5]所提算法与本文所提信道分配算法进行对比。从图3中可以看出,本文所提信道分配算法能效略低于文献[4-5]所提算法性能,而优于等信道增益间隔信道分配算法和随机配对算法。 图3 平均系统能效与次用户基站总功率的关系 图4 用户公平性指数与次用户基站总功率的关系 同时从图4中可以看出,Jain公平指数随着基站总功率值的增加而减少。此外,与其他4种信道分配算法相比,所提算法可以获得更好的公平指数,这表明所提算法具有良好的公平性。 图5描述了不同功率分配算法情况下,平均系统能效与次用户基站总功率的关系,其中,每个子信道最多复用3个用户。从图5中可以看出,次用户基站总功率存在一个满足最优系统能效的功率点,称该点为绿色通信点。当基站总功率小于该绿色通信点时,所提算法能够实现最大化系统能效,当基站总功率大于该点时,所提算法依然能够保持最优能效,而分数功率分配算法和固定功率分配算法以及OFDMA系统的能效却逐渐下降。当基站总功率为20 dBm时,所提算法性能分别优于分数功率分配算法0.13%、固定功率分配算法4.43%,OFDMA系统18.56%。当基站总功率为30 dBm时,所提算法性能相较于分数功率分配算法、固定功率分配算法和OFDMA系统,分别增长了44.7%,46.18%和58.6%。 图5 平均系统能效与次用户基站总功率的关系 图6描述了不同功率分配算法情况下,平均系统能效与最小吞吐量的关系,其中,基站总功率为30 dBm。最小吞吐量越大,表示对系统所需的最低消耗功率就越大。从图6中可以看出,当最小吞吐量值小于4时,系统平均能效首先略微上升然后略微下降,当最小吞吐量值大于4时,系统平均能效明显开始减小。此外,所提算法的平均系统能效始终优于其他3种算法,这表明了所提算法的有效性。 图6 平均系统能效与最小吞吐量的关系 图7描述了不同功率分配算法情况下,平均系统能效与主用户干扰功率的关系,其中,基站总功率为30 dBm,用户最小吞吐量为1 bit/s/Hz。从图7中可以看出,当主用户干扰功率取值为-90~-80 dBm时,系统能效为0。这是因为主用户干扰功率取值较小限制了基站的总发射功率,从而导致基站可用功率较小,而此时基站可用功率无法满足所有用户的最小吞吐量要求,所以基站停止提供服务,系统能效为0。当主用户干扰功率取值超过-80 dBm后,系统能效逐渐增加,直至收敛到固定值。这表明当基站总功率一定时,存在一个主用户干扰功率最小值点。当主用户干扰功率取值小于该点时,基站发射功率受主用户干扰功率限制,当超过该点时,基站始终能够以最大功率服务用户。 图7 平均系统能效与主用户干扰功率的关系 本文针对认知无线电网络中的非正交多址下行链路,研究了联合优化信道分配和功率分配算法以最大化系统能效。考虑基站总功率限制,次用户最小吞吐量限制和主用户干扰功率限制以及子信道最大可接入用户数限制,构建能效优化资源分配问题。为了解决该问题,将原始问题分解为信道分配问题和功率分配问题。针对信道分配问题,首先阐述了现有低复杂度信道分配算法的原理,然后针对此类算法的不足,通过引入比例公平系数,构建了新的子信道调度准则,进而提出了一种次优公平性可调的信道分配算法,并详细描述了所提信道分配算法的原理。针对功率分配问题,基于所提信道分配算法的结果,由于该问题是非线性分式规划问题,所以采用连续凸近似,变量替换等操作将非线性问题等效转化为凸问题,然后采用Dinkelbach算法进行求解,最后仿真验证所提算法的有效性。 虽然本文对认知无线电网络中的非正交多址子信道内的功率分配和信道分配算法做了大量的研究,力争在研究中做到深入且全面,然而本文所涉及到的内容尚不够完善,还需要进一步研究,如应更加考虑子信道间的功率分配问题。在本文的研究中,为了方便计算,假设子信道之间进行均等功率分配算法,然而均等功率分配算法并没有考虑子信道的信道增益问题,因此,其更适合信道之间相互独立的场景,故不能很好地提升时变场景下的系统性能。因此,在未来的研究中,子信道之间的功率分配问题可以作为一个研究重点。2.2 功率分配算法




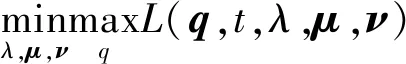



3 仿真与分析
3.1 算法复杂度分析

3.2 仿真结果

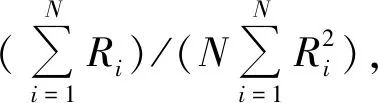


4 结 论
