基于GRNN的永磁力矩电机复杂轨迹进给位置误差预测研究*

于嘉龙，彭宝营，侯明鹏，杨庆东，耿冬冬

(1.北京信息科技大学 机电工程学院，北京 100192；2.北京机科国创轻量化科学研究院有限公司，北京 100084)

0 引言

永磁力矩电机具有高转矩密度、响应快速、无中间传递环节等优点，在数控机床和仿真转台等需要直接驱动、运行平稳、快速响应和高精度的控制系统中得到了越来越多的应用[1-3]。永磁力矩电机广泛的应用在高精度位置伺服系统中[4-5]。位置传感器相对于转子实际位置的偏差是指转子位置零位偏差也即位置传感器的零位偏差。位置误差是衡量定位精度高低的指标。在伺服系统等高精度控制的场合一般需要安装位置传感器来获得电动机转子的准确位置。由于安装的误差会使位置传感器的零位产生偏差，位置传感器的零位偏差将造成转子位置检测的零位偏差，而电动机转子检测零位偏差的存在引起逆变器开关逻辑换向错误，将引起不期望和不可控制的轴电流，严重时会造成电动机无法启动或转动[6]。

近年来，国内外学者研究主要集中于位置误差对力矩电机产生的影响和位置误差的补偿方面的研究。王向军等[7]从影响转矩测量结果的力矩电机定转子之间的轴向误差和力矩电机测量装置中转矩传动轴与力矩测量轴之间的径向误差两方面出发，分析两种误差对于测量结果的影响，并通过最小二乘线性拟合的方法，确定他们与转矩测量结果之间的关系。言钊等[8]对位置误差进行检测在进行补偿。上述对力矩电机的复杂轨迹位置误差预测的研究较少。

由于力矩电机直接作用于负载，在加工过程中，由于自身的齿槽力矩、电磁效应和加工装配工艺等产生的转矩波动直接传递到负载上，从而对系统的平稳性及位置精度产生影响。基于上述问题，本文提出了使用广义回归神经网络进行力矩电机的转子位置误差进行预测研究，并采用试验台采集的数据进行训练预测。

1 GRNN力矩电机位置误差预测方案

1.1 广义回归神经网络基本原理

广义回归神经网络(Generalized Regression Neural Network,GRNN)是美国学者Donald F·Specht在1991年提出的，是径向基函数神经网络的一种特殊形式，用密度函数来预测输出[9-10]。广义回归神经网络属于有导师学习法。GRNN建立在非参数核回归基础上，样本数据作为后验概率验证条件执行Parzen非参数估计，从样本中计算自变量和因变量之间的联合概率密度函数，算出因变量对自变量的回归值[11]。

径向基函数作为隐单元的“基”，构成隐含层空间。隐含层对输入样本进行变换，将低维空间的模式变换到高维空间内，使得在低维空间内的线性不可分问题在高维空间内线性可分。因此在结构上GRNN包含输入层、隐含层、求和层和输出层，输入层到隐含层采用径向基函数变换，隐含层到输出层采用特殊线性变换[12]。

1.2 GRNN模型计算方法

广义回归神经网络的理论基础是非线性回归分析[13]。设随机变量x和随机变量y的联合概率密度为f(x,y),若已知x的观测值为x0，则y相对于x的回归，也即条件均值：

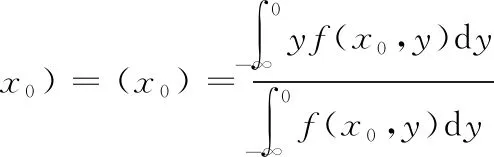
(1)

根据Parzen非参数估计，由x和y的样本数据集可计算除密度函数f(x0,y)

(2)

d(x0,y0)=(x0-xi)T(x0-xi)/2σ2

(3)

d(y0,yi)=(y0-yi)2∕2σ2

(4)

上式中，n为样本容量，p为随机变量x的维数，σ为光滑因子，实际上就是高斯函数的标准差。将式(2)、式(3)、式(4)代入式(1)并交换积分与求和的顺序，有：

(5)

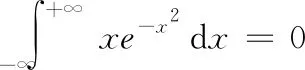
(6)

化简上式，可得：

(7)

1.3 力矩电机位置误差GRNN模型拓扑结构

本系统采用4层GRNN预测力矩电机位置误差。考虑到力矩电机在运动过程中， 指令位置和加工速度直接影响力矩电机的位置误差。而且这些因素间存在着一定非线性关系。广义回归神经网络对非线性映射问题可以实现任意逼近。本文将以正弦信号的指令位置和指令速度为GRNN估算模型输入变量，以三角波信号的位置误差为模型输出建立GRNN模型。用此来完成复杂轨迹的位置误差预测。用到的输入样本数据为力矩电机走正弦波的实际运行数据,共40组。用到的输出样本数据为力矩电机走三角波的实际运行数据,共10组。

在确定力矩电机位置误差预测模型的输入、输出参数后，模型的输入层和输出层的神经元的节点数也随之确定下来。由于模型的输入向量为3维、输出向量为1维，故可以确定输入层的神经元个数为3个，输出层的神经元个数为1个。研究表明，GRNN隐含层神经元节点个数按照训练样本数据量进行确定，而求和层的神经元节点数为2。

广义回归神经网络拓扑结构包含输入层、隐含层、求和层、输出层，建立力矩电机位置误差GRNN模型拓扑结构如图1所示。

图1 力矩电机位置误差GRNN模型拓扑结构

2 GRNN位置误差模型训练及结果分析

2.1 GRNN算法的实现

本文是借助Matlab2014a进行编程预测。在Matlab2014a中，使用newgrnn()函数可以快速建立一个神经网络，调用方式如下所示：

net=newgrnn(p,t,spread)

(8)

其中，net=newgrnn()用于创建一个GRNN网络;p为训练样本；t为训练样本目标值；spread为径向基函数的分布密度，默认值为1。但是通常spread越小，网络的逼近效果越好，因此，在网络设计过程中可以调整spread的值，确保达到比较理想的预测效果。本文将spread选取为0.3。

2.2 样本数据采集实验平台

永磁力矩电机位置误差数据采集平台主要包括控制系统、运动系统和采集系统，控制系统包括工业控制柜、PMAC运动控制器、大族伺服驱动器、上位机、数据总线；运动系统包括磁粉制动器、PSN型功率放大器、永磁力矩电机、固定支座、加载装置；采集系统包括圆光栅、数据采集卡。磁粉制动器和永磁环形力矩电机固定在平台上，两者通过弹性联轴器进行连接，转矩波动通过磁粉制动器内置扭矩传感器进行测量。

图2是实验采集平台的控制流程图。通过上位机中PMAC自带的PEWIN32PRO软件进行运动指令的编写和发送，将运动指令通过控制器的A/D转换发送到力矩电机中，从而实现电机运动。同时反馈检测元件将检测到的数据传回到上位机，PEWIN32PRO软件对数据进行分析研究从而实现实时误差的补偿。力矩电机贴有圆光栅角度测量仪，用于检测伺服电机输出跟踪回转角度偏差。圆光栅角度测量仪测量获得角位移信号，并通过反馈装置传输到工控机中作为实时反馈信号。

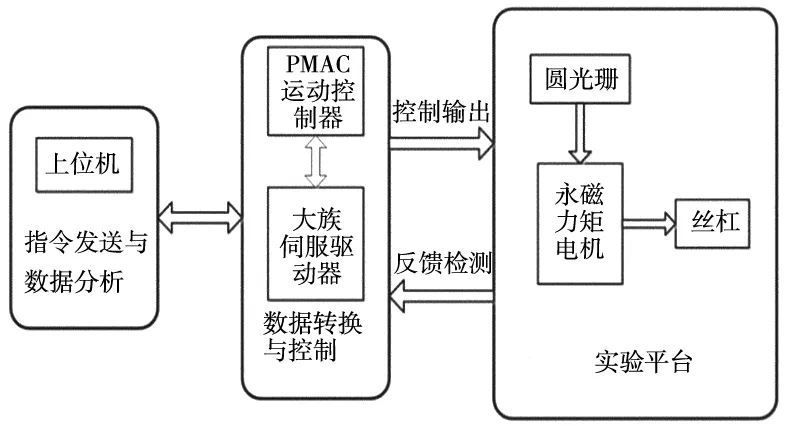
图2 实验采集平台控制流程图

其中，PMAC运动控制器是用来接收上位机的指令，并将控制指令通过伺服驱动器传给电机，通过数据采集卡、圆光栅来测量力矩电机旋转的角度与角位移并将数据传送上位机进行分析和研究。用此方法来实现对力矩电机的转子位置、速度等的控制。还可以运用PMAC运动控制器自带的软件对力矩电机进行PID整定以及对速度、位置、加速度等数据的采集与分析。

2.3 预测数据分析

因为本文采集的输入数据的单位不一样，像指令速度的输入数据的范围特别大，导致的结果可能是GRNN神经网络训练时间长,运算速度比较慢，所以要将数据进行归一化处理。即将三个影响位置误差的数据和要输出的数据的范围变成[-1，1]。归一化的处理公式如下所示：

Y=2×(xi-xmax)/(xmax-xmin)-1

(9)

其中，xmax是一组数据中的最大值，xmin是一组数据中的最小值，xi是当前值，Y为归一化之后的数据。

本文建立的GRNN预测模型。该模型以影响力矩电机转子位置误差的各因素为输入,位置误差为输出。训练样本为力矩电机平台实时采集的40组正弦波行走方式产生的运行数据，然后采用10组三角波行走方式产生的运行数据来验证模型的精确性，以达到复杂轨迹的预测研究。

为了测试广义回归神经网络永磁同步电机的位置误差预测结果的优越性，本文选择了基于BP神经网络的预测模型、基于Elman神经网络的预测模型与基于广义回归神经网络的预测模型进行对比，分别统计他们对永磁同步电机的预测精度，并从中抽取6组预测精度，结果如图3所示。

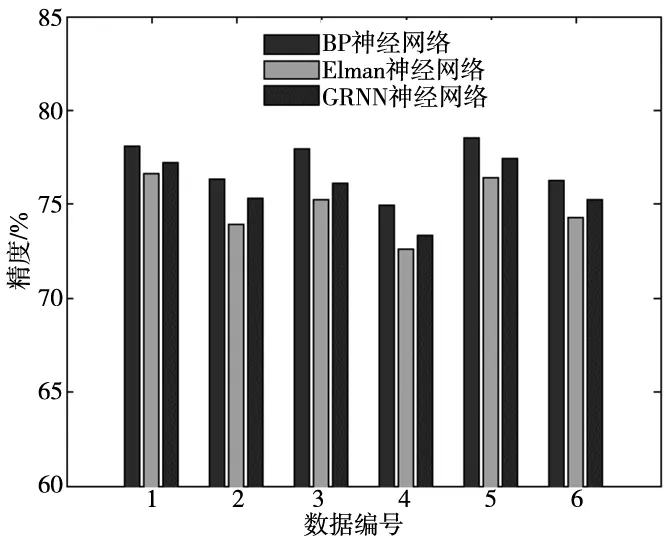
图3 与其他模型的位置误差预测精度对比

从图3可以看出，相对于其他力矩电机位置误差预测模型，广义回归神经网络具有较好的位置误差的预测效果，同时还发现广义回归神经网络也要明显的比其他的位置误差预测模型的运行时间要快，明显的提高了力矩电机位置误差的预测效率，从中抽取6组的运行时间对比如图4所示。

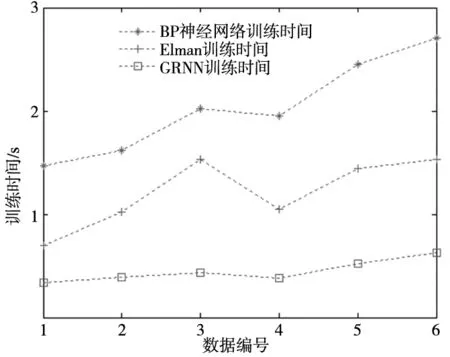
图4 与其他位置误差预测模型的预测运行时间对比

本文有十组预测数据进行预测，其中只拿出一组典型的预测结果在图5进行显示。

图5 GRNN训练结果显示

本文将拿出一部分实验值和广义回归神经网络预测值，以及相对误差对比如图6所示。

图6 误差分析图

从图6可以看出，广义回归神经网络模型预测的永磁力矩电机复杂轨迹位置误差预测的最大相对误差是6.51%，由此可知广义回归神经网络能够快速有效的预测出力矩电机复杂轨迹位置误差，提高了永磁力矩电机复杂轨迹位置误差的预测效率。

3 结论

位置误差作为衡量高精度系统的主要指标,对运动系统乃至整个永磁同步电机组都有着重大影响。准确快速的预测位置误差,能够对机械加工平台的稳定运行起到推动作用。传统的BP模型和Elman模型可以很好的预测位置误差,但将预测模型换为GRNN后,模型的预测精度又提高了一定的精度。因此，对力矩电机的位置误差预测能够在一定程度上对整个永磁同步电机的运行起到一定的指导意义。