基于改进DDE算法的协同目标分配问题研究
2019-12-26欧峤贺筱媛郭圣明
欧峤 贺筱媛 郭圣明
在一体化联合作战的作战筹划阶段,协同目标分配是在态势评估和威胁评估的基础上进行作战力量运用的匹配优化,也可视为在体系对抗的过程中实时分配可用的作战力量攻击预定目标.在军事运筹领域,协同目标分配通常被规约为兵力分配、火力分配或武器目标分配(Weapon Target Assignment,WTA)等问题,本质上是一类组合优化问题,具有多约束、非线性、多目标等特点.协同目标分配包含时间协同、任务协同和效果协同三类因素,涉及规划和调度两个领域,决定着兵力分配运用的科学性和合理性,是将作战意图落地为作战行动序列的关键步骤.
1 协同目标分配问题研究现状简析
当前,关于协同目标分配的研究,主要存在两个方面的问题:一是现有问题模型还不够逼真,不能完整体现现实约束条件和指挥员的核心关注点;二是现有方法还难以满足体系对抗中实时求解大规模目标分配问题的需求.
1.1 现有模型考虑与对抗相关的因素还不够
战役指挥员在联合作战指挥控制中,其注意力一般集中于关照战役全局、把握战役进程、掌控战役节奏、关注重要攻击/防御方向和核心战役行动设计上.假如将指挥员在协同目标分配过程中的核心关注点用军事运筹学语言描述出来,可概括为“在保证作战效果的基础上尽量提升作战效费比,即在一定的限制条件内,用最小的作战资源消耗代价完成对预期作战目标的攻击”.
在任务规划系统中,当态势认知模块完成态势评估、威胁评估等步骤后,通过目标选择模块输出明确的打击目标清单,协同目标分配作为连接目标选择和协同航迹/路径规划的关卡,主要解决的是协同攻击、协同防御、协同侦察中“谁来做”“用什么做”两个问题.科学合理的协同目标分配模型既要满足作战行动的客观限制条件,也要符合某种战场态势下指挥员的核心关注点.目前的协同目标分配模型考虑时间、空间、火力资源等约束较多,考虑威胁联网环境下的突防概率、实体间的关联关系等与对抗相关的因素还不够[1-7].
1.2 现有方法难以满足大规模目标分配实时性需求
在“快吃慢逐步取代大吃小”的时代,OODA 环的转速在很大程度上决定着是否能够取得最终的作战胜利.1986 年,Lloyd 等[8]证明了WTA 问题是NPC 问题.NPC 问题的特性是随着问题规模的扩大,求解最优解的时间将成指数级增长.此外,NPC 问题也可能因全局最优解不在割裂的解空间内,导致最终只能求到全局次优解或局部最优解[9].
在兵力分配运用的过程中,科学、高效的协同目标分配方法对提高作战实体的生存概率、任务完成率和资源利用率都具有十分重要的意义.目前,解决协同目标分配问题较为成熟的方法中,匈牙利法、分支界定法、隐枚举法、混合整数线性规划法、动态规划法等传统数学规划方法,编程繁琐,难以处理变量维数较大的问题,在求解大规模问题时收敛速度很慢;合同网协议[10-12]、拍卖法[13]等市场机制法具有“原理简单”、“易于实现”、“执行效率较高”等优势,但也存在“算法设计过程中需要人工定义大量的协同规则”、“求解大规模问题时收敛速度较慢”、“处理协同关系和约束条件的能力较差”、“有较大概率因通信速率的限制或敌方电磁干扰的影响而失效”等劣势;人工神经网络[14]、模拟退火算法[15]、遗传算法[16]、差分进化算法[17]、蚁群算法[18]、粒子群优化算法[19]等智能优化算法,因具有易于实现、计算复杂度低、性能优越等优点,被大量运用于目标分配问题的研究中.在使用过程中,研究者们从不同角度、不同环节对各种算法进行了改进或组合,产生了许多混合优化算法,在解决不同场景的目标分配问题上取得了较好的效果,但是在面对大规模问题时,目前的算法仍普遍存在早熟收敛和进化缓慢等现象.
2 协同目标分配问题模型
作为指控决策中的关键环节之一,协同目标分配方案的实时性、准确性、有效性将直接影响在体系对抗中己方能否取得更高的整体作战效费比.
2.1 基本假设
现假设通过前期的预警、侦察行动已获取较为完整的敌方作战体系情报信息,并以此构建出联合火力打击的目标体系.依据指挥员和参谋机关于t时刻的态势分析结果,假设在(t,t+Δt) 的时段内敌我博弈态势不会出现瞬时突变,即将未来时段的战场态势视为相对静止状态,通过目标选择模型得出需要实施打击的N个基本目标,分别记为T1,T2,··· ,TN.当前己方作战体系内可用的作战力量有M个武器平台,分别记为P1,P2,··· ,PM,分散部署于多个空间位置,隶属于相应的作战部队.可用于本波次联合火力打击的武器平台数量和弹药数量上限分别为QPl和QWk.协同目标分配的理想方案是满足各种约束条件且能够被执行的协同攻击计划,可用带索引标签的二维矩阵x来表示,行名和列名分别表示己方可用的武器平台和基本目标的唯一识别号,xi j表示第i个武器平台攻击第j个基本目标所使用的主战武器数量.
2.2 约束条件定义
执行作战任务通常受限于敌情、我情、战场环境等主客观因素,为便于定量决策,特将相关约束条件作如下定义.
2.2.1 火力资源约束
任何一个波次的联合火力打击行动,实际投入的作战资源数一般应小于或等于预期计划投入,并且也应小于或等于未来一段时间内作战部(分)队能够提供的最大作战资源数.武器数量约束可如式(1)表示:

武器平台数量约束可如式(2)表示:

2.2.2 打击要求约束
凡已列入某个阶段打击目标清单的目标,应至少被一个武器平台攻击,可如式(3)表示:

与传统目标分配模型不同,本文将打击每个基本目标的毁伤要求视为约束,具体情况如式(4)所示:

式(4)中,PFj表示己方作战体系对第j个目标的侦察概率,Pi j表示武器平台Pi使用武器Wl对第j个目标的单发毁伤概率,bj表示对第j个目标的毁伤要求.
2.2.3 武器目标匹配约束
根据武器装备的实际性能,选择恰当的武器去攻击特定的目标,往往能取得更好的作战效能.在火力打击任务中,一般需依据匹配表来选择合适的作战武器.如果武器Wi与目标Tj之间符合适用约束,则可表示为:
否则,应表示为:

2.2.4 作用范围约束
作用范围约束主要包括两个方面,一是武器平台的最大机动作战半径,二是作战武器的射程,前者受完成时限、速度、航程等因素的限制,后者是作战武器的一项基本战技性能指标.两者之和应大于或等于己方武器平台与某一基本目标之间的距离.
2.2.5 威胁联网环境下的突防概率
威胁联网[20]的概念最初由Robert 于1999 年提出,它表示多个威胁源在互联互通的信息系统的支撑下,通过一体化预警探测系统发现、识别目标并引导火力单元实施拦截攻击.威胁联网环境下的突防概率主要由敌方作战体系对己方武器平台的探测概率、杀伤概率以及因系统繁忙而未被服务的概率共同决定.其中,联网后的雷达系统对空中目标的探测概率可表示为:
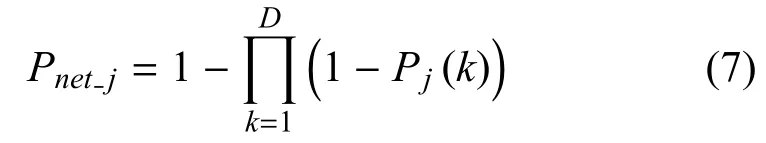
式(7)中,D表示威胁联网雷达的数量,Pj(k)表示第k个雷达对第j个空中目标的探测概率.
威胁联网导弹防御系统对同一目标的杀伤概率可表示为:
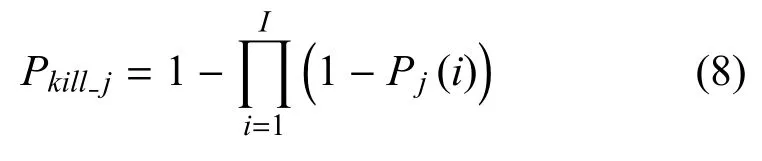
式(8)中,I表示威胁联网防空导弹发射单元的数量,Pj(i)表示第i枚导弹对第j个空中目标的杀伤概率.
空中目标因综合导弹防御系统因导弹发射单元繁忙而未被服务的概率πj可表示为:

式(9)中,I表示威胁联网防空导弹发射单元的数量,λ 表示目标流速度,µ表示防空导弹的拦截打击效率.因此,第j个空中目标的突防概率可表示为:
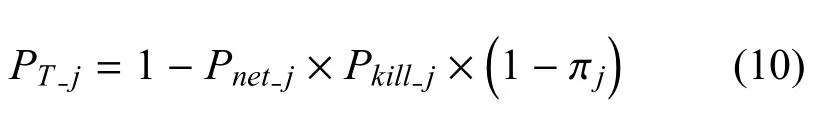
2.3 协同目标分配数学模型
结合上一小节的定义与分析,协同目标分配问题的数学模型可如式(11)所示.

其中,Ci表示第i类作战武器的价值系数,xi j表示第i个武器平台打击第j个目标消耗的武器数量,PTi表示武器平台Plati在执行火力打击任务可能被敌方作战体系摧毁的概率,可由式(10)得出,Vi表示武器平台Plati的价值系数,rangePi是武器平台Plati的最大机动作战半径与武器Wl的射程之和.
3 改进DDE 算法求解协同目标分配问题
差分进化算法(Differential Evolution,DE) 源于Price 在1994 年提出的遗传退火算法,后经Storn 和Price 改进后,较好地解决了超30 维的切比雪夫多项式系数求解问题,之后又被Storn 成功应用于解决中心选址和组合优化问题.实验表明,DE 算法在求解标准测试函数和实际工程优化问题方面,其性能均超过了遗传算法、模拟退火算法、粒子群优化算法等多种智能优化算法,是当前最好的优化算法之一[21].
3.1 基本原理
与大多数进化算法一样,DE 算法是一种基于种群迭代进化的优化算法,它进化的基础源于当前种群的变异、重组和选择,进化的方向指引是通过比较适应度函数值来得到的.与其他进化算法的不同之处在于,DE 算法的关键进化信息来自从当前种群中随机抽取的个体向量间的比例缩放差分量.
3.1.1 差分变异
DE 算法的变异策略有十多种,较为常见的策略如表1所示:

表1 DE 算法的常见变异策略
变异算子F决定着算法的搜索步长,其经验取值范围为[0.5,0.9];F的取值越大,算法的探索能力越强,取值越小,算法的开发能力越强.
3.1.2 均匀交叉
为完善进化策略,DE 算法引入了离散重组方法(也称均匀交叉).均匀交叉操作在不改变向量参数取值的前提下,分别从当前的目标种群和变异种群中选择两个索引序列号相同的个体向量xi,j,g和vi,j,g,通过特定的交叉继承规则来构造试验向量ui,j,g.具体组织方式如下:
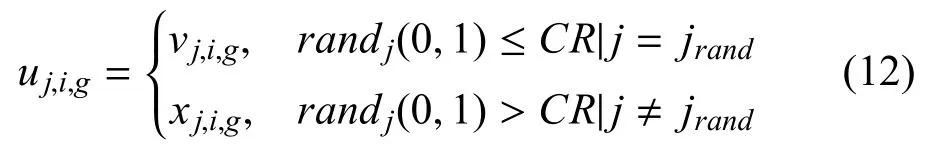
randj(0,1) 是均匀分布的随机数,交叉算子CR的经验取值范围为[0.1,0.9].此外,为了防止试验向量有概率完全复制目标向量的参数信息,DE 算法通过随机选取整数jrand∈[1,2,··· ,D],无论随机数randj(0,1)与交叉概率CR的比较结果如何,当分量维数j与jrand相等时,试验向量的第j维分量参数信息将强制从变异向量中获取.
3.1.3 贪婪选择
与其他优化算法一样,DE 算法通过比较适应度值来确定是否保留目标种群的父代个体向量进入下一轮的种群进化中去,这种“优胜劣汰”的贪婪法则将保证目标种群逐步向全局最优解靠拢.具体的选择依据如式(13)所示:
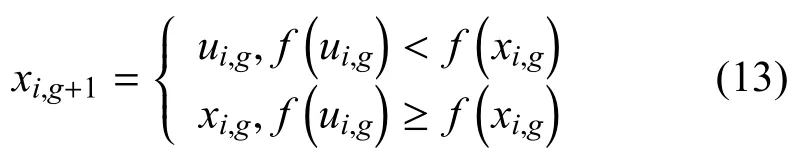
3.2 算法改进思路
依据第2 节建立的协同目标分配问题数学模型,一般可将该问题规约为不等式约束条件下的整数规划问题.传统的DE 算法主要为了解决高维多项式参数拟合问题,假如要将其应用于含有强约束条件的整数规划问题,必须对其进行改造,改造的基本目的有3 个,一是将算法转换为符合问题特点的离散差分进化算法(Discrete Differential Evolution,DDE),二是为了让种群中个体向量能够满足问题需求,三是为了让种群在搜索优化的过程覆盖更多的可行域范围,且尽可能让更多的种群个体逐步靠近可行域并最终停留在可行域中.具体的改进方式有以下几个方面.
3.2.1 种群初始化
与遗传算法一样,DDE 算法对初始种群有较强的依赖.为确保初始种群的多样性,使个体尽可能覆盖更多的可行域范围,本文借鉴了合同网协议(Contract Net Protocol,CNP) 的思想,采用直接处理约束的方法是将最优化问题转化为约束满足问题,以此来确保初始种群质量.
3.2.2 自适应变异
在基本DE 算法中,变异算子F一般取常数,但在实际操作过程中,F的取值往往难以把握.取值较大时,算法探索能力增强,开发能力减弱,求解结果的精度降低;取值较小时,算法开发能力增强,种群多样性变低,容易出现早熟收敛的现象.为兼顾算法的种群多样性和求解精度,避免早熟收敛,可将F调整为自适应变化,设计方式如式(14)所示:

式中,F0、gmax和g分别表示变异算子的初始取值、最大迭代进化次数和当前的迭代进化次数.
3.2.3 随机交叉
交叉算子CR控制着种群个体的交叉变异概率,为进一步确保算法不会早熟收敛,CR的初始取值可为0.1.此外,为保持种群在搜索进化过程中的多样性,特让交叉算子处于一个随机动态取值范围,设计方式如式(15)所示:

3.2.4 约束处理
在贪婪选择阶段,目标种群和试验种群的个体将进行逐一比较,借鉴Pareto 占优排序的思想,可将个体向量符合约束条件的程度及适应度值的大小都纳入比较的范围,该步骤可确保子代种群均处于可行域范围内,也利于加速算法的寻优收敛.
3.2.5 算法描述
利用改进DDE 算法求解协同目标分配问题,输入为打击目标清单、毁伤概率表、敌方作战体系基本信息和己方可用的武器平台清单等,输出为表示协同目标分配方案的二维矩阵.算法基本流程如表2所示.

表2 改进DDE 算法基本流程
4 实验验证
4.1 实验设计
为验证改进DDE 算法求解协同目标分配问题的性能,本节中将通过一组小规模数据进行测试.假设现有10 个武器平台可用,需从中选出合适的武器平台对8 个目标进行打击,要求必须达到最低毁伤要求,并使得弹药消耗和武器平台预计战损的整体价值最小.
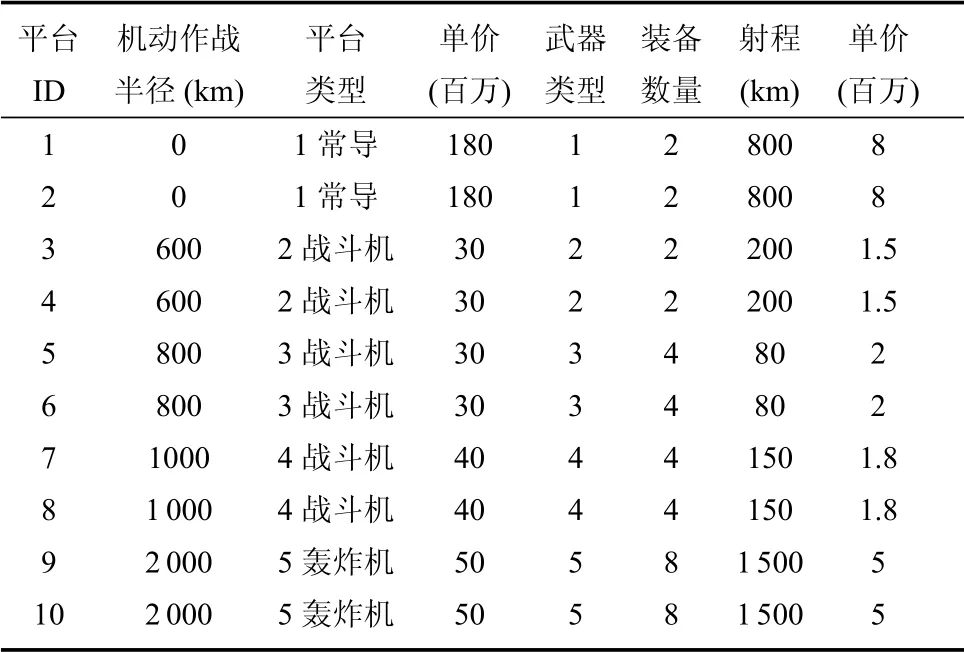
表3 武器平台信息表
打击目标清单信息如表4所示:

表4 打击目标清单信息表
武器打击目标的毁伤概率如表5所示:
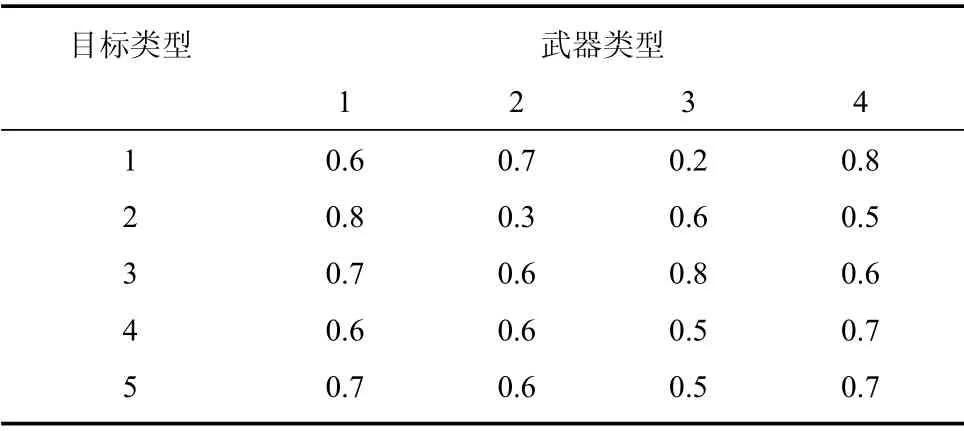
表5 武器-目标毁伤概率表
武器平台携行的作战武器与目标的匹配关系如表6所示:

表6 弹目匹配关系表
4.2 改进DDE 算法与传统DDE 算法的比较
将表3~表6的数据分别导入改进DDE 算法和传统DDE 算法的程序中,程序分别运行20 次.迭代次数gmax=400,种群个体数Np=80,差分变异算子初值F0= 0.7,交叉算子最低值CR= 0.1,最佳适应度值的曲线如图1所示.
如图1所示,虚线和实线分别为改进DDE 算法与传统DDE 算法的收敛曲线,改进DDE 算法基本每次都能逼近全局最优解,最佳适应度值为77.78,最长用时15.1 s;而传统DDE 算法迭代400 次的最佳适应度值为96.48,迭代800 次后适应度值才能下降到80 以下,与改进后的DDE 算法相比差距较大.从实时性和有效性两个角度进行分析,改进DDE 算法基本满足求解大规模协同目标分配问题的需求.

图1 改进DDE 算法与传统DDE 算法收敛情况对比
5 结论
协同目标分配既是作战协同的重要组成部分,也是任务规划系统的重要模块.本文从体系对抗的角度综合考量作战体系的整体作战收益和作战资源损耗,除了将传统限制条件纳入约束范围,还将武器平台在威胁联网环境下的突防概率融入协同目标分配的数学模型中.此外,为使离散差分进化算法能够有效解决复杂约束条件下的组合优化问题,本文在种群初始化、差分变异、均匀交叉、贪婪选择等4 个环节分别对算法进行了改进,有效加速了算法的寻优收敛,为实时求解对抗条件下的协同目标分配问题探索了一条方法路径.
