基于隐马尔可夫模型的目标航迹匹配方法∗

张宏宇 陶 智

（1.91001部队 北京 100000）（2.海装装备项目管理中心 北京 100000）

1 引言

近年来，随着我国国家实力的增强，海上目标的行为活动规律备受关注。在海上目标侦查监视过程中，目标经常在某个海域附近进行着相似的侦查活动，这使得目标的运动航迹具有较强的相似性。通过对目标动态航迹与目标历史航迹进行关联匹配分析、判断目标的活动规律已经成为海上侦查监视工作的重要任务之一。

动态航迹指的是雷达对某个空中或者海上移动目标在运动过程中采集得到的位置、时间、方向及速度等数据按照时间先后顺序构成的运动数据。依据动态航迹在历史航迹大数据中匹配与目标航迹最为相似的航迹数据，从而识别出动态航迹的目标属性。此类问题实际上可以归类为轨迹匹配问题，通过一定的匹配算法计算多条轨迹之间的相似程度，从而为后续的轨迹聚类、目标识别、个性化推荐或其它相关应用提供相应的技术支持［1］。

现有的匹配方法根据使用的信息可以分为三类：1）几何匹配方法，2）概率统计匹配方法以及3）其他高级匹配方法。几何匹配方法可以归纳为三类，点到点的匹配方法［2］，点到线的匹配方法［3］以及线到线的匹配方法［4］。点到点的匹配方法计算探测点与候选轨迹中每个节点的距离，然后将探测点匹配到距离最近的节点上。点到线的匹配方法计算探测点到候选轨迹的投影距离，然后选择最近的轨迹作为匹配轨迹，相应的投影点就是匹配节点。线到线的匹配方法将探测到的整条轨迹与候选轨迹进行相似性比较，最终选择相似度最高的候选轨迹。几何匹配方法的优点在于计算简单，效率较高，但是适应性以及稳定性较差，精度较低，难以满足实际的复杂应用需求。

基于概率信息，Ochieng等［5］提出了针对复杂道路网络中的地图匹配算法；文献［6～7］提出了置信区间匹配方法，基于多假设思想，在置信区域内选出多条航迹加入到候选航迹中，然后对每条候选航迹都计算出一个得分，最终选择得分最高的航迹作为匹配航迹。基于概率的匹配方法推导比较复杂，实现比较困难；并且算法计算开销较大，匹配准确性较低，难以满足实时性需求。

高级匹配方法往往使用综合信息，使用机器学习或数据挖掘方法来完成匹配过程，具体包括卡尔曼滤波［8～9］，隐马尔可夫模型［10～11］等。基于卡尔曼滤波中的白噪声假设，通过分析卡尔曼滤波后的模型误差特性是否满足高斯白噪声分布来完成匹配过程。隐马尔可夫模型是一种全局匹配算法，可以综合距离、方向等多个约束获取最佳的轨迹序列。相对于前述的其他匹配方法，使用综合信息的匹配算法准确率较高，算法的适应性也更好，算法本身也更加稳定。

现有的轨迹匹配工作主要集中于室外空间或路网空间中，而针对于航迹匹配的研究较少。其次，在现有的少量雷达航迹匹配的相关研究中，往往只考虑距离因素［12］，而忽略了航向、速度、方位、仰角以及高度等重要的运动特征信息，难以满足复杂的应用需求。第三，现有研究往往关注离线、或者是静态航迹的相似性，对于动态航迹、实时航迹的相似性关注较少。因此，针对现有研究状况的不足，本文展开相应的研究工作，其主要内容包括以下几点：1）由于隐马尔可夫模型被广泛应用于轨迹匹配中，并且匹配精度和稳定性明显优于其他方法，因此，本文采用隐马尔可夫模型来进行雷达航迹相似性匹配，以及相应的软件设计；2）本文中对现有的隐马尔可夫模型进行了相应的改进，加入了航向因素，使用综合信息来完成匹配过程；3）基于现有的雷达航迹历史数据，进行仿真实验和测试，实时计算显示航迹与历史航迹的匹配结果，并且在界面上显示相应的匹配概率；4）根据雷达航迹相似性匹配结果，完成基于活动规律的目标识别。

2 研究方法

隐马尔可夫模型（Hidden Markov Model，HMM）最早是在20世纪60年代由Baum等在一系列统计学论文［13～15］中提出和描述的，主要应用在语音识别、行为分析、自然语言处理等领域。隐马尔可夫模型可以解决三类问题：1）评价问题，将最可能的情况与观测序列匹配，使用前向算法求解（Forward algorithm）；2）解码问题，使用维比特算法（Viterbi algorithm）确定最可能产生观察序列的隐藏序列；3）学习问题，使用前向-后向算法（Forward-backward algorithm）确定模型最可能产生的观测序列。航迹匹配问题实际上可以归类为一个解码问题。基于HMM的航迹匹配是在给定序列前提下，寻找产生这一观测序列的隐藏序列。其中，观测序列表示雷达探测获得的航迹点，而隐藏序列表示运动目标的历史航迹构成的航迹网。

在基于HMM的航迹匹配算法中，对于每一个雷达探测点，存在多个候选航迹。当前雷达探测点在这些候选航迹上的投影视为候选航迹点，在隐马尔可夫模型中作为顶点（如图1所示），并且具有一个观测状态概率，表征探测航迹点是否与候选航迹匹配的可能性。探测点与候选航迹的距离越近，则观测概率值越大。然后，计算马尔可夫链中连接相邻顶点的边权重，称为状态转移概率。最后，在马尔可夫链中寻找使观测概率和转移概率的乘积最大化的最优路径，一般使用维比特算法来进行求解。维比特算法实际上是一个动态规划算法，在这里被用来解决隐马尔可夫模型中的预测问题。

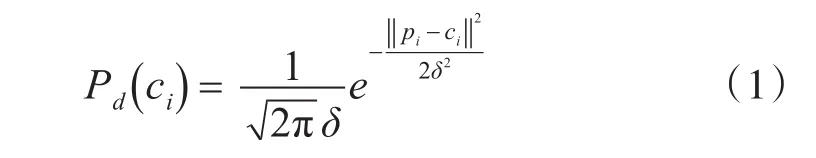
在隐马尔可夫模型中，最关键的步骤是计算观测概率和转移概率。雷达探测航迹点的测量误差可以被合理的描述为一个雷达探测点和历史实际路段之间距离的高斯分布（式（1））。其中，高斯分布中的均值μ取0，标准差δ取10km，可根据具体实验尺度进行调节。

ci表示马尔可夫链中的候选点，‖‖pi-ci表示探测点与候选航迹点之间的空间距离。两者之间的空间距离越近，则计算得到的观察概率越大。

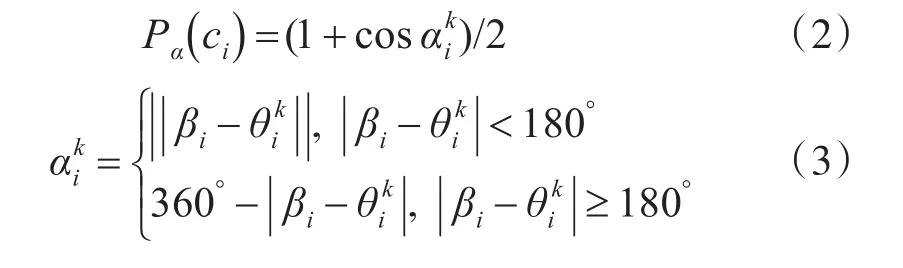
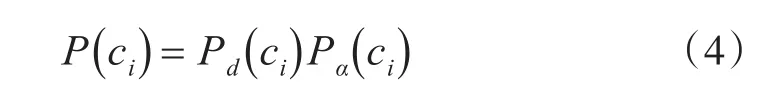
在Newson等［11］的算法中，观测概率仅与距离因素相关。然而，在实际应用中，观测概率也需要考虑方向权重［16］，因此，本研究中对观测概率的计算进行了改进，加入了航向因素，具体计算方法如式（2）、（3）、（4）所示。式（2）为航向因素的观察概率的计算公式，其中为速度方向与匹配航迹路段的夹角。以正北方向为基准，分别计算探测航迹以及历史航迹与正北方向的夹角，标记为 βi和的计算方法如式（3）所示。综合距离因素和航向因素，观测概率的计算公式可以标记为二者的观测概率积（见式（4））。

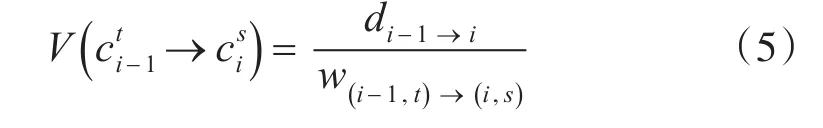
本研究中传递概率的计算基于如下假设：运动目标总是选择空间距离最近的路线航行，前后航迹中的距离越小，其传递概率越大。转移概率V的计算方法如式（5）所示，根据前后两个时间点t和s之间的探测点 pi-1、pi及其候选点的信息，推测从 pi-1到 pi的真实路径是到最短路径的可能性。其中，di-1→i表示两个探测航迹点之间的空间距离；w(i-1，t)→(i，s)表示两个候选点之间的最短航迹距离。这样匹配出的结果可以避免出现绕路航行或者航迹不连续的情况。

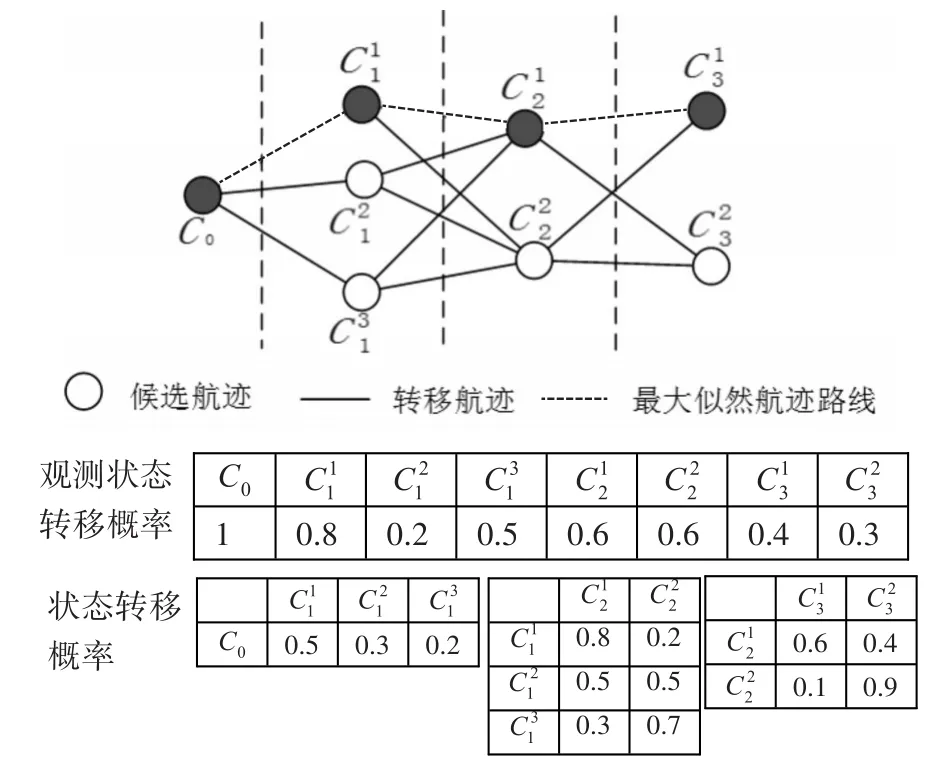
图1 基于隐马尔可夫模型的航迹匹配过程示例

基于HMM的航迹匹配过程可计算出各候选点的观测概率及各候选点的转移概率（如图1所示）。具体计算过程如下：从c0开始，c0有3个候选点，它们的总概率分别为0.8×0.5=0.4，0.3×0.2=0.06，0.5×0.2=0.1。其中最大值为，于是c0成功匹配到。接下来对于，先计算路径=0.6×0.8=0.48，同理计算路径的得分等于max｛0.4+0.6×0.8，0.06+0.6×0.5，0.1+0.6×0.3｝，即为0.88。然后，针对每个候选点重复上述过程，算法最终得到的匹配结果为。

3 仿真验证分析

3.1 实验流程

仿真系统为多平台多目标场景，模拟输出目标的真实动态航迹，其具体的实验验证流程如图2所示。首先，根据历史航迹数据完成建库和索引工作。在实际的验证过程中，为了提高实时计算的效率，根据目标属性建立了三个数据库，分别为空客A320、波音737以及波音747等民航航班的历史航迹数据库。其次，为了提高历史航迹搜索效率，本文中采用R树［17～18］索引来查询历史航迹数据。R树是一种与B树相类似的高度平衡树，它被广泛应用到空间数据库当中，用于解决传统数据库索引检索空间对象效率低效的问题。

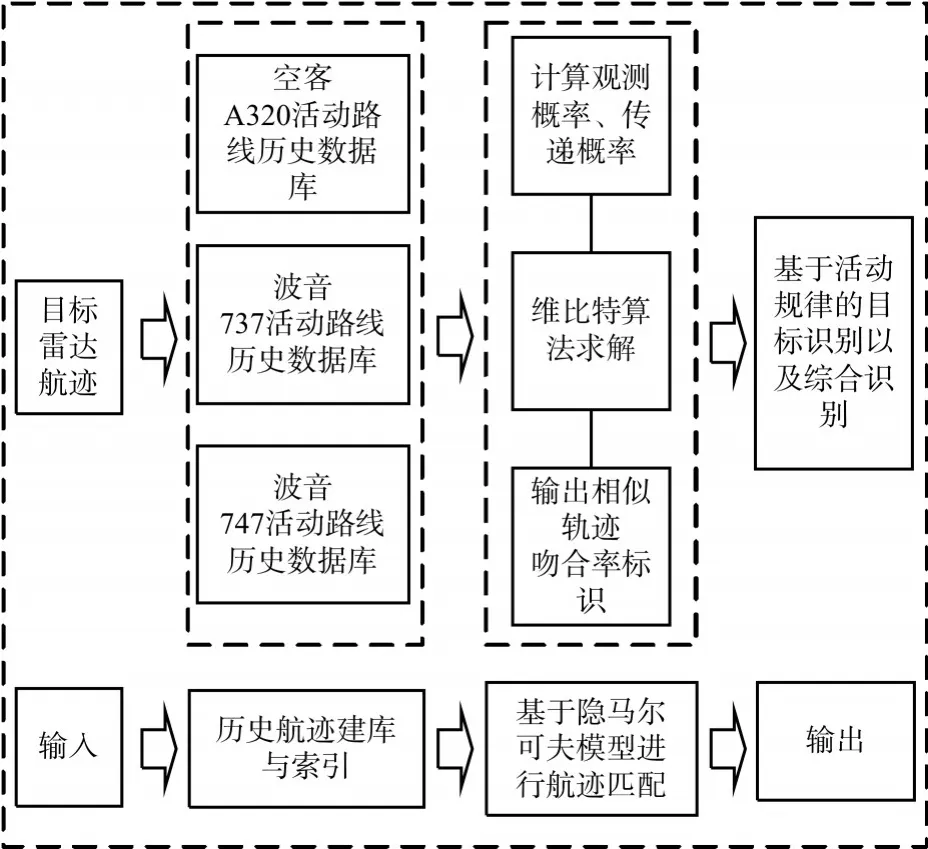
图2 仿真试验流程图

然后，采用隐马尔可夫模型进行航迹匹配。根据第二部分方法中介绍的观测概率和传递概率的计算方法，分别计算得到各个候选航迹的观测概率和传递概率。在观测概率计算过程中，需要考虑距离和航向等多重运动特征因素，综合衡量航迹间的相似性。最后使用维比特算法求解出相似路径，同时输出每条路径的匹配概率。

在实际的计算过程中，对三个历史航迹数据库分别进行建模和索引，减轻索引负担，同时并行计算以提高计算效率。此外，分别计算三个历史航迹数据库中的航迹匹配概率，取最大值分别标记为P1，P2，P3，并且以百分比的形式显示在活动规律识别界面上。最后，根据上面计算得出的匹配概率，选择最大值，标记目标属性。例如，如果P1值最大，则该飞行目标为空客A320的可能性最大，因而被标记为空客A320。从而完成基于运动特征的目标识别，进一步辅助综合识别等其他应用。

3.2 实验结果分析

仿真验证的具体实验结果如图3所示。基于空客A320、波音737和波音747历史航迹数据，实验使用隐马尔可夫模型计算仿真动态航迹和历史航迹的匹配概率，并且将匹配概率值以百分比的形式标记在界面上。目标运行过程中，基于隐马尔可夫模型的匹配过程动态进行，界面上显示的匹配概率动态更新，实时显示运动目标的局部匹配结果。运动目标停止后，界面上显示运动目标航迹的全局匹配结果。

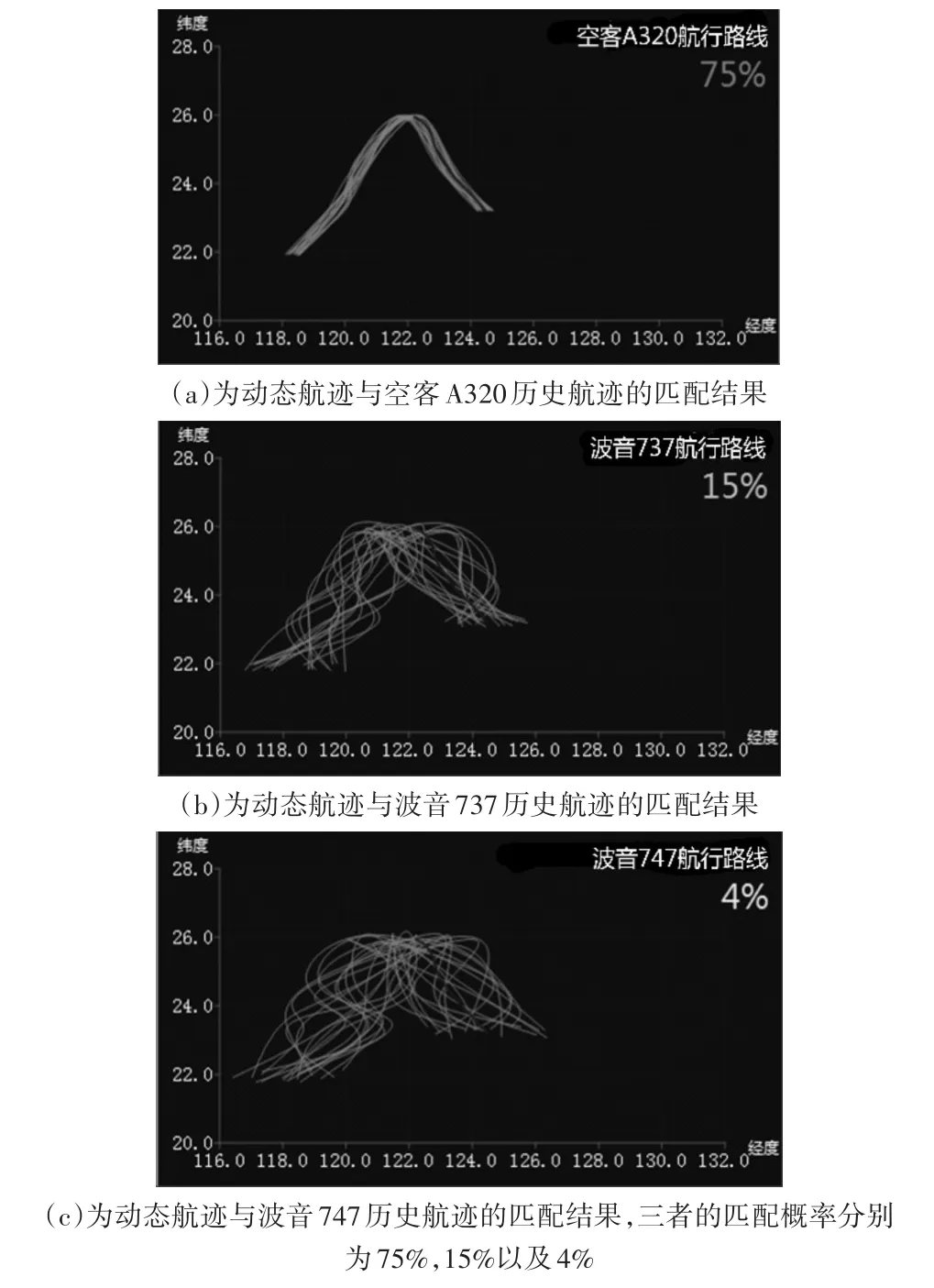
图3 动态航迹匹配结果图

如结果所示的全局匹配结果，动态航迹与空客A320活动路线的匹配概率为75%，与波音737历史航迹的匹配概率为15%，与波音747历史航迹的匹配概率为4%。由此可以得到，该模拟航迹与空客A320活动路线的匹配概率最高。因此，从活动规律上判断，该运动目标最有可能归属于空客A320。同时将该匹配概率结果发送给综合识别模块，辅助目标进一步识别。

4 结语

本文针对仿真系统多目标平台时，雷达输出目标航迹与历史航迹的相似性问题，采用隐马尔可夫模型来进行目标航迹与历史航迹之间的关联匹配。该算法突破了目标航迹与历史航迹长度不一致限制、航迹不连续的限制，并且能够有效地消除噪声点的影响，对于航迹的关联匹配具有较好的计算能力。基于隐马尔可夫模型的雷达航迹关联匹配方法已经应用在实际工程中，初步实现了基于活动规律的目标识别，为进一步的综合目标识别奠定了基础。

然而，本文实现的航迹匹配方法仍然存在一定的局限性，具体表现为仅仅考虑了航迹的空间距离和航向相似性，并未考虑时间因素［19］、其他多特征因素［20］以及位置语义特征［1］对航迹匹配的影响。其次，现有的方法适用于简单场景，暂时未对复杂场景做匹配分析研究。因此，在后续的研究中，研究方向主要体现为以下两点：1）继续补充多特征以及多维度相似性度量因素，为综合匹配识别提供更加有效的依据和证据；2）根据具体应用需要，因地制宜，提高算法对复杂场景的匹配效果和效率，实现航迹的精准化关联匹配。