抑制单脉冲雷达角闪烁方法研究∗

郑守铎 张雷雷 范庆辉

（1.92941部队 葫芦岛 125001）（2.北京遥感设备研究所 北京 100854）

1 引言

随着精确制导技术的发展，末制导雷达定位精度不断提高。根据理论和实践分析，在远距离上，由热噪声引起的角度测量误差是主要误差成分，而在近距离上，目标角闪烁引起的测角偏差占主导地位［1～4］。

复杂目标不同部位的散射强度和相对相位的随机变化，造成回波相位波前面的畸变，波前在接收天线口径面上的倾斜和随机摆动必然引起测角误差，即角闪烁。当目标接近雷达时，角闪烁大小可能使雷达指向目标尺寸外，角闪烁成为目标近距离跟踪的主要跟踪误差源［5～6］，因此必须对角闪烁进行有效抑制，以提高末制导雷达的定位精度。

文献［7～8］研究了加权测角方式抑制角闪烁的方法，在抑制舰船目标的角闪烁时获得了良好的结果，文献［9］引入中值滤波抑制角闪烁。针对近距离舰船目标回波MTD处理后，舰船目标跨越多个多普勒单元，使用区域平均加权方法解算角误差，再对测角结果以小窗口中值加权滤波方式进行处理。

2 振幅和差式单脉冲测角原理

振幅和差式测角原理［10～12］是在同一角平面内发射两个相同但部分重叠的波束，将其接收信号进行和差处理。如果目标处于两波束的重叠方向（称为等信号方向），则两波束收到的信号强度相同，否则一个波束收到的信号强于另一波束收到的信号。

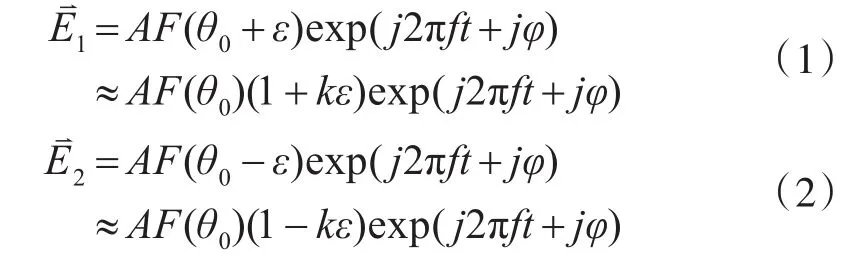
假设系统中不存在幅度或相位不平衡，天线和差器的两个输入端的信号为式（1）、式（2）中，A为雷达方程决定的常数，θ0为波束偏角，F(θ)为雷达波束方向性函数，ε为目标偏离等信号强度点的角度，φ为回波信号初始相位为归一化常数（角误差斜率）。

一般来说，和差信号经过A/D转换器、数字下变频、正交解调后，和差信号分解为同相和正交相两部分，角误差可表示为

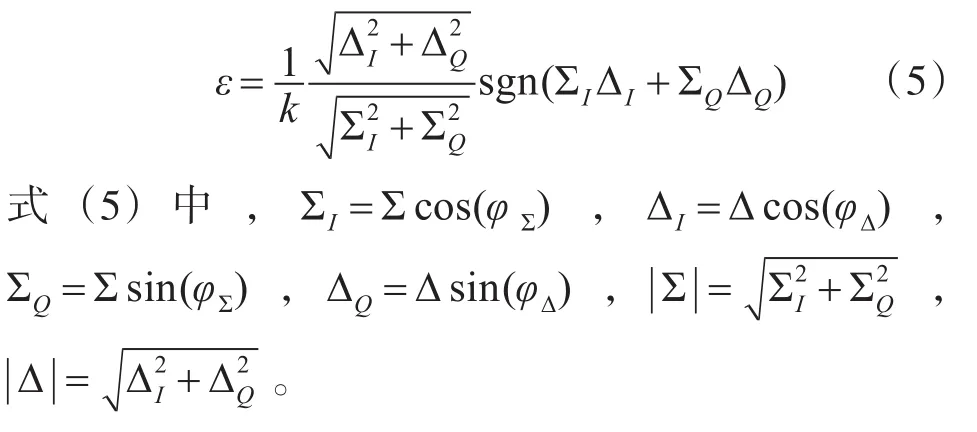
一般来说解算角误差使用的是非相参积累或相参积累以后的数据，本文计算角误差使用的是相参积累后的数据。

多个脉冲积累可以有效地提高信噪比，从而改善雷达的检测能力，在检波前的积累称为检波前积累或中频积累。信号在中频积累时要求信号间有严格的相位关系，即信号是相参的，所以又称为相参积累。零中频信号保留了相位信息，可实现相参积累，这是当前比较常用的方法，它将接收到的N个回波经过相参积累后达到同相叠加的目的。

对于接收到的N个脉冲，每个脉冲分别给出n个采样点，每个脉冲中第i个（1≤i≤n）样点对应的位置相同，以保证其相位相同，将N个脉冲纵向累加，即相参积累。对相参积累结果进行求模所形成的三维图反映了目标的距离-多普勒特性，所以此图也称为R-D图。

3 跟踪点选择

回波幅度最大的散射中心作为跟踪点能抑制其它散射点对测角精度的影响，但如果回波幅度最大的散射中心其回波幅度随弹目的相对运动或目标姿态的改变而起伏不定，会导致测角误差偏大，甚至角跟踪失败。

而舰船目标在R-D图上一般要跨越几个多普勒单元，选最大值点并不能完全使用R-D图信息，而合理使用R-D图信息才可减小目标的幅度起伏、角闪烁等的影响，获得稳定的角跟踪效果。

以和通道最大值的0.8倍作为门限，过门限的点保留，差通道选择与和通道对应的位置，使用这些点分别计算角误差，若共取得N个角误差信号序列，每个角误差信号对应一个目标视在位置，用点(x1，y1)，(x2，y2)，…，(xN，yN)表示，并用 (xm，ym)表示 N个回波的加权中心，Ai表示每个回波的幅度，则

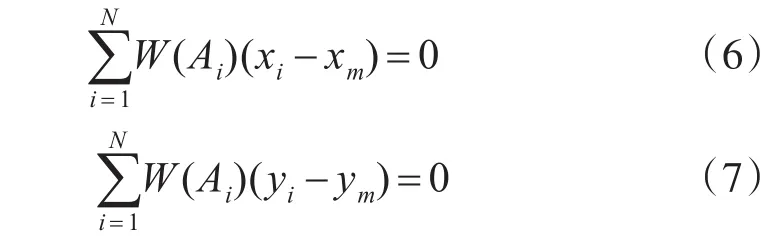
式（6）、（7）中，W(Ai)是对应点 (xi，yi)的加权幅度。

上式可写成：

由于W(Ai)除以任何因子都不影响(xm，ym)，因此，权函数W(Ai)可以归一化。

若以角误差形式表示，则上式可改写为

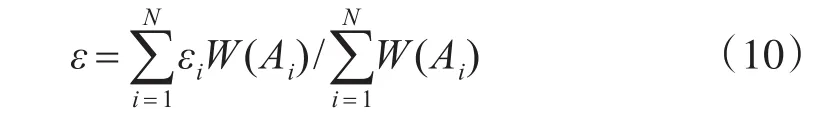
文献［3］中提出抑制角闪烁比较好的方法是将各角误差平均加权作为输出的角误差，即：

4 改进的中值滤波方法

中值滤波可对长拖尾概率分布的噪声起到良好的平滑效果，且其运算量小，在工程上广泛应用。文献［9］采用标准中值滤波方法抑制角闪烁，标准中值滤波对滤波窗口内数据做排序（由小到大或由大到小），取排序后的数据中位于中间的元素的值（所谓的中值）作为输出值。但标准中值滤波仅仅使用了邻域的统计信息，破坏了邻域的空间和结构信息，为此本文使用一种改进的中值滤波算法，以降低标准中值滤波对邻域空间和结构信息的破坏。

改进的中值滤波算法为：对滤波窗口内数据做排序（由小到大），取排序后的数据中位于中间的元素值及前后各一个元素，并采用以下加权方式计算出滤波值。

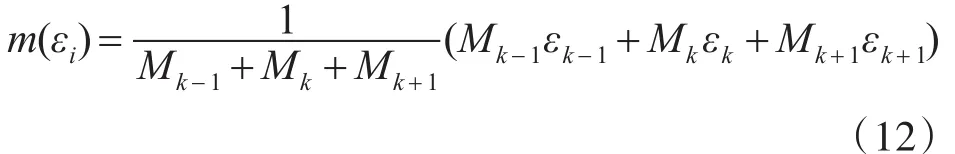
Mk为εk对应目标区域的最大值。

本文在仿真时滤波窗口选为11，则改进算法可以表示为

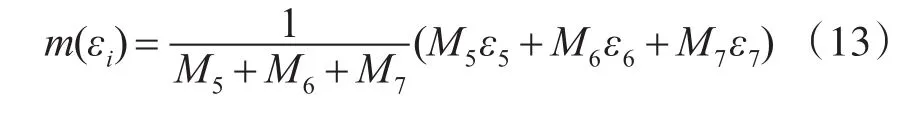
5 试验结果

试验数据使用某雷达照射8km、6km处运动的舰船所采集到的数据，由于海面波动使船发生颠簸，船的姿态变化复杂，使船的起伏和角闪烁均较强。

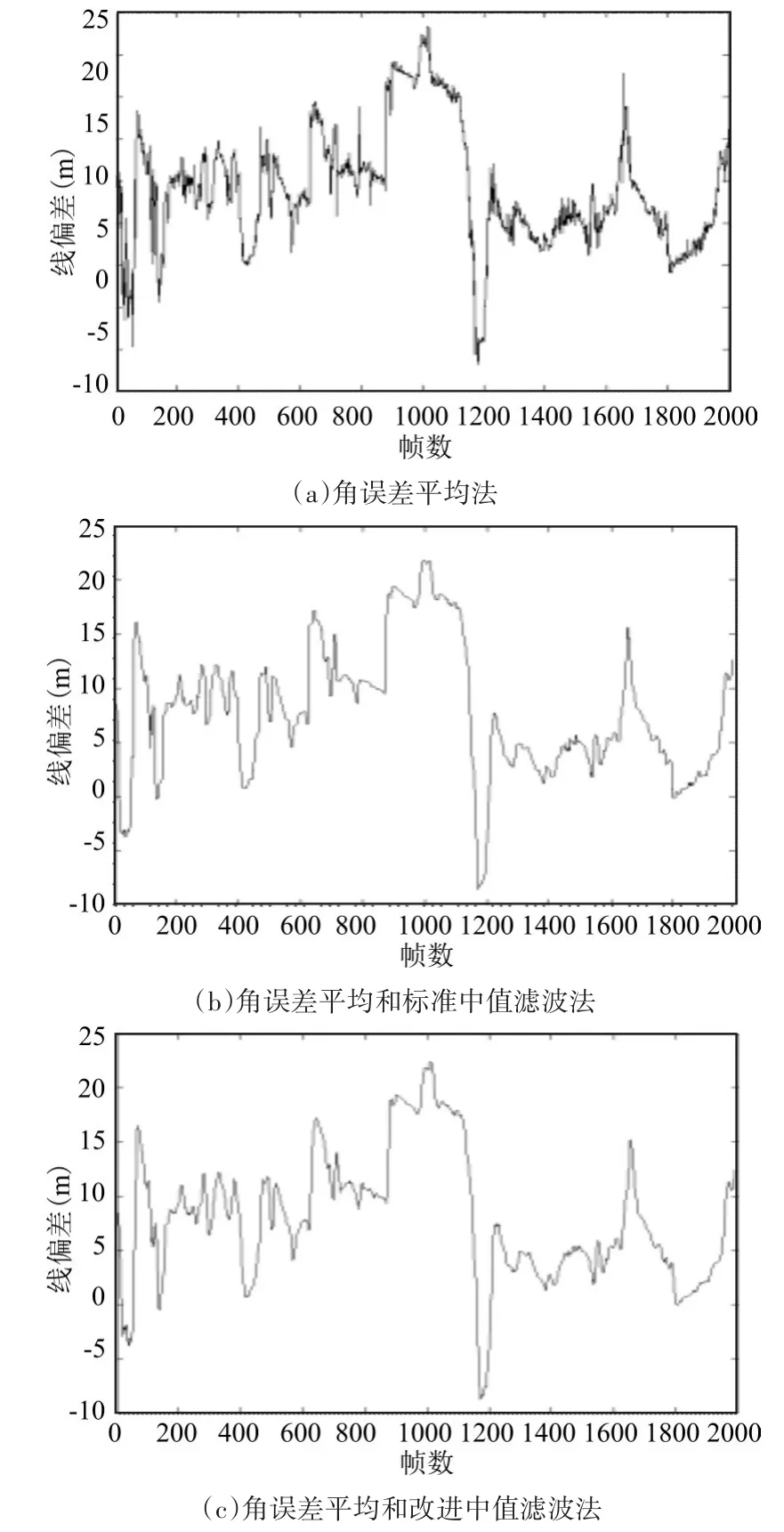
图1 舰船在8km处计算出的角闪烁

图1 （a）中角误差平均法角闪烁的均方差为6.5259m，图1（b）中角误差平均和标准中值滤波法联合使用角闪烁的均方差为6.0519m，图1（c）中角误差平均和改进中值滤波法联合使用角闪烁的均方差为5.9304m；图2（a）中角误差平均法角闪烁的均方差为9.2051m，图2（b）中角误差平均和标准中值滤波法联合使用角闪烁的均方差为7.9273m，图2（c）中角误差平均和改进中值滤波法联合使用角闪烁的均方差为7.8061m；由此可见角误差平均和标准中值滤波联合使用可有效降低角闪烁效应，而改进的中值滤波方法降低标准中值滤波对邻域空间和结构的破坏，在保留角误差细节的同时改善了角闪烁的抑制能力。

图2 舰船在6km处计算出的角闪烁

6 结语

对近距离舰船目标回波进行相参积累处理后，舰船目标一般要跨越几个多普勒单元，区域均匀加权法跟踪点选择方法可以抑制角闪烁；改进的中值滤波方法降低标准中值滤波对邻域空间和结构的破坏，在保留角误差细节的同时改善了角闪烁的抑制能力，此方法可有效减小目标角闪烁对跟踪的影响。