可拆解组合式船舶结构关键方法研究
2019-12-26张荣鑫
张荣鑫
(中国船级社大连分社 大连116013)
引 言
随着国际对石油、天然气等需求的不断扩大,勘探范围也在海洋和内陆湖泊之间不断转换。中国石油集团在进行全球石油勘探作业时就需要采用组合式气枪震源船。该船主要能够用于沿海遮蔽区域、滩涂区域以及从海上难以直接驶入的港湾区域进行勘探作业。由于有些区域船舶无法直接驶入,必须通过陆路运输才能进入,需要把船体分解成若干个模块进行运输,到达作业区域后再组装成整体实现作业需要,这样能降低生产成本,提高设备使用效率。
船体各模块间采用螺栓连接并能使其达到相应的强度、稳性等要求,从而满足CCS 规范要求。由于该类船舶属于新颖设计,现阶段无相应的规范要求及设计标准,因而在设计和结构审核中就需要综合考虑各方面因素,使其既合理可行,又能与规范的要求趋于一致。
该船结构设计的关键技术主要包括:一是确认横舱壁连接处螺栓强度如何满足总纵强度、横向强度的要求;二是确认纵舱壁连接处螺栓强度如何满足横向强度的要求;三是确认其他部位如艏楼与主甲板间、甲板室与主甲板间及甲板室之间、舷墙与主甲板间等螺栓强度。本文提出了船体梁-螺栓强度等效原则和横向结构-螺栓强度等效原则,并参考集装箱惯性力理论、船首上浪力及锚机锚泊力等综合因素,对以上三方面关键技术的螺栓强度进行分析,圆满地完成了审核任务。该船于2013 年建造完毕,运营航行于各水域进行勘察作业,为我国石油勘探发挥了应有的作用。
1 具体案例
案例船为可拆解组合式震源船,主要工作区域为沿海或内陆河、湖,实船如图1 所示,主尺度参数见表1。

图1 组合式气枪震源船实船

表1 案例船主尺度参数
全船共分为12 个模块,主甲板以下有7 个模块(悬艉部1,艉部P/S 各1,中部P/S 各1,艏部P/S 各1),艏楼1 个模块,甲板室4 个模块。
甲板纵/横向螺栓布置情况如下页图2 所示。具体的螺栓座及螺栓连接详图见下页图3 所示,其中螺栓三视图见图3(b),其余类似;螺栓底座与船体结构直接焊接,如图3(a)中红圈内所示;螺栓底座接触处为凹凸式阶梯状结构,如图3(a)、(b)中蓝圈内所示,螺栓不承担剪力,底座部分承担剪力;横舱壁处的螺栓轴向为船长方向,纵舱壁处甲板/船底的螺栓轴向为船宽方向。
2 船体梁—螺栓强度等效原则
由于船体结构的复杂性,通常将船体视为理想化的一变断面空心薄壁梁。船体总纵弯曲发生在两个平面:垂直平面和水平平面。船体梁抵抗在外力作用下沿其纵向垂直/水平面内所发生的弯曲能力为总纵强度。由于作用于船体上最多力的方向是垂直的,当船舶迎浪航行时,在垂直平面内弯曲引起的应力对总强度是决定性的。确定船体总纵弯曲应力计算方法的选择取决于载荷特性、船舶主尺度的比值、所确定的船体应力-应变状态成分的类型以及计算精度的要求[1]。
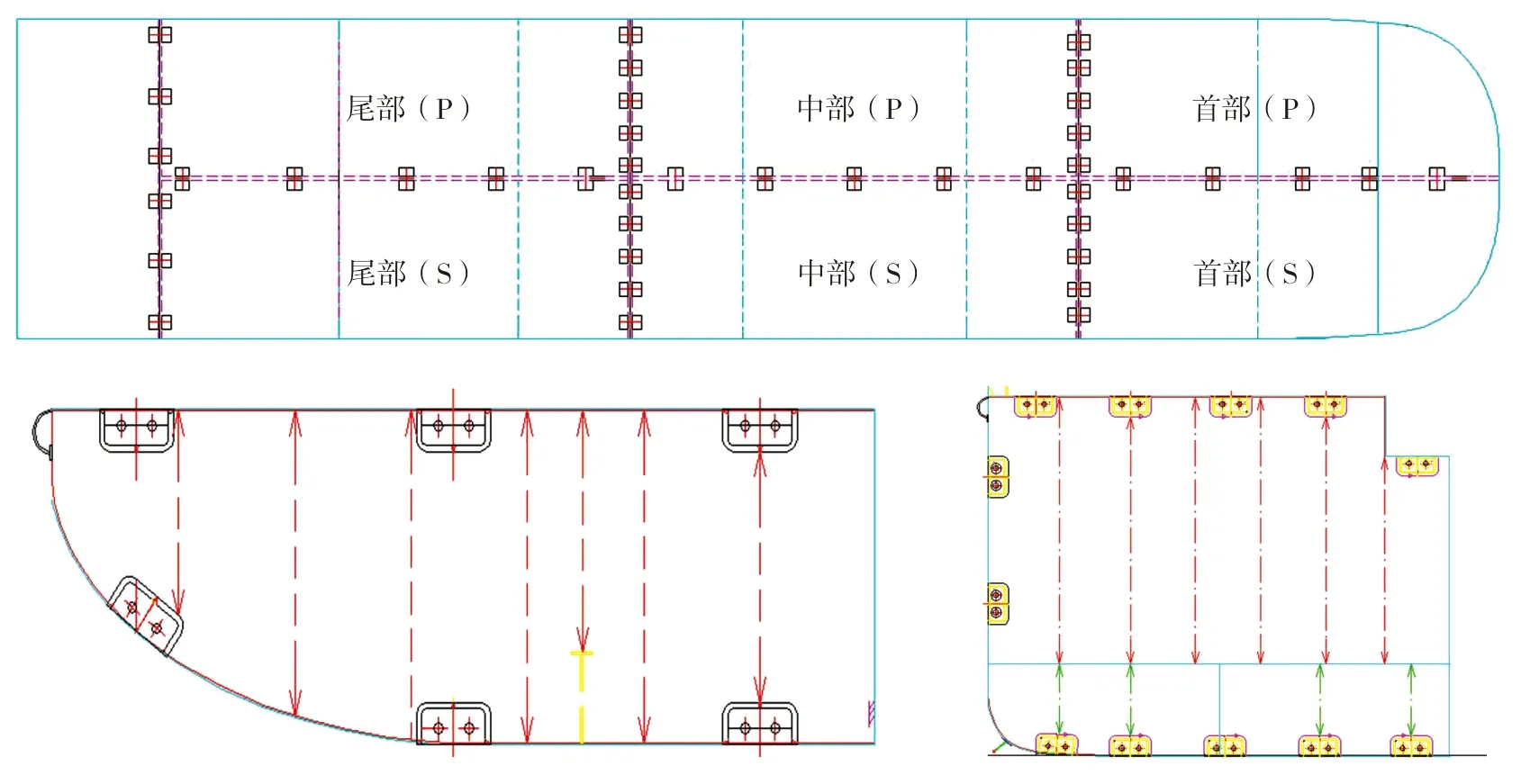
图2 螺栓布置图(甲板&横舱壁)
船体是在自平衡作用下弯曲的非等剖面梁。按照平剖面和法向剖面假设在船体纵向构件中的法向应力按下式[2]确定:

式中 :σ为应力,N/mm2;M为弯矩, KN·m;I为惯性矩,cm4;z为中和轴到构件的距离, m。
作为梁弯曲工程理论基础的假定体系含有一定的矛盾,如式(1)必须在船体剖面没有剪应力为前提,但实际上剪应力存在。为了确定剪应力采用茹拉夫斯基定理,按式(2)确定:

式中:τ为剪应力,N/mm2;S为位于要确定应力的高度上面/下面的横剖面截取部分的静矩,cm3;δ为船体横剖面轮廓在该高度处的总厚度,mm。
最大法向应力发生在距剖面中和轴最远的构件上,而最大剪应力发生在中和轴上。如果船体有些结构由弹性模量Ei的材料建成,它不同于基本船体材料的弹性模量E0,则这些构件的剖面面积应带有等于比值λ=Ei/E0的相应折减系数计入等值梁内[1]。
可拆解组合式船舶纵向各模块间采用螺栓连接,因而导致了其纵向构件的不连续性(参见图1所示)。船体梁-螺栓强度等效原则就是船体梁纵向螺栓连接处其惯性矩/剖面模数不变原则,保证船体梁的总纵强度不变,即此处螺栓强度与船体梁强度等效。根据该原则及CCS 规范[3]对船体总纵强度横剖面的计算要求,假定横舱壁螺栓连接处的用螺栓替代船体板及纵向构件时,仅承受总纵弯曲不承受剪力,则满足:

式中:IV1和IV0分别为螺栓处横剖面垂向惯性矩与船体横剖面垂向惯性矩,cm4;IT1和IT0分别为螺栓处横剖面水平惯性矩与船体横剖面水平惯性矩,cm4;WD1和WD0分别为螺栓处横剖面甲板处剖面模数与船体横剖面甲板处剖面模数,cm3;WS1和WS0分别为螺栓处横剖面船底处剖面模数与船体横剖面船底处剖面模数,cm3;S1和S0分别为螺栓处横剖面面积与船体横剖面面积,cm2。
由于螺栓的弹性模量未知,以材料的屈服强度代替弹性模量,则λ=σ1/σ0,其中σ1和σ0分别为螺栓和船体材料的屈服强度。由于该剖面还存在剪力,剪力设计为由螺栓座承受(螺栓不承受剪力),则该处承受剪力面积应满足:

式中:δ1为螺栓处底座抗剪面面积,cm2。
由此可见,船体纵向模块连接处满足式(3)和式(4),则满足船体梁-螺栓强度等效原则。
3 横向结构—螺栓强度等效原则
横向强度是船体横向结构抵抗相应外力的能力。通常横向强度计算仅考虑船体所承受的各种局部载荷及舷外水压力的作用,不考虑船体梁弯矩(包括垂向和水平)的作用。
由于可拆解组合式船舶纵舱壁结构间也采用螺栓连接(见图1),当船舶在斜浪或横浪航行时,船底/舷侧受到不对称波浪力,从而对螺栓产生力。考虑到该种应力水平较低且与CCS 规范对船体横向强度要求类似,本文参考CCS 规范提出了横向结构-螺栓强度等效原则,即螺栓强度应能承受除船体梁弯矩(包括垂向和水平)以外的载荷及舷外水压力能力。
CCS 规范[2]对船体横向强度计算采用FEM 方法,其舷外水压力载荷由静水压力和波浪水动压力两部分组成,载荷作用分布情况见下页图4 所示。
在基线处:
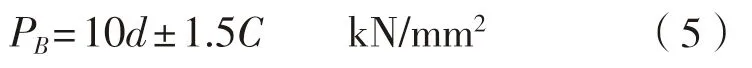

其中:
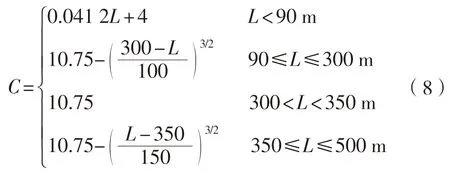

图4 载荷作用分布情况
式中:L为船长,m;d为吃水,m;D为型深,m。
P0按式(9)计算:

计算工况分为对称工况和非对称工况,计算衡准如表2 所示,仅考虑连接船体横向结构的螺栓强度,其边界条件为两端横舱壁处全约束。

表2 计算衡准N/mm2
4 等效计算
4.1 船体梁—螺栓强度等效计算
本文采用CCS 规范计算软件COMPASS,计算螺栓连接处的横剖面特性,其中定义A 剖面为船体纵向构件剖面,B 剖面为螺栓构件剖面(螺栓定义为梁结构,按照实际尺寸建模;剖面中板厚为0 mm,仅将螺栓计入横剖面特性计算),具体模型如图5 所示。
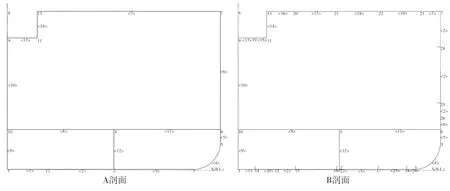
图5 横剖面模型
COMPASS 计算A、B 横剖面特性,结果见表3。

表3 横剖面特性计算结果
由表2 可知,maxλ= 2.694,螺栓为M42,8.8级(屈服强度640 N/mm2),而λ=σ1/σ0= 640 / 235=2.723 均大于2.694,所以螺栓强度满足要求。另外由于剪应力由螺栓座承受(螺栓座结构参见图2),经计算δ1/S0= 8 553 / 1 675 = 5.11 ≥1,满足设计要求。
综上,横舱壁间承担总纵强度的螺栓强度满足等效原则,达到设计要求,不需要进行其他方法校核。下文对连接船体结构横向构件的螺栓利用有限元法进行验证。
4.2 横向结构—螺栓强度等效计算
根据文中第3 节的横向强度校核方法,本文使用MSC Patran/Nastran 软件,仅对纵舱壁连接处的甲板/船底螺栓及螺栓底座结构强度进行校核,有限元模型包含甲板板、纵/横舱壁板、甲板板、实肋板、螺栓底座板等采用板单元模拟,扶强材、甲板横梁、螺栓等采用梁单元模拟,如图6 所示。
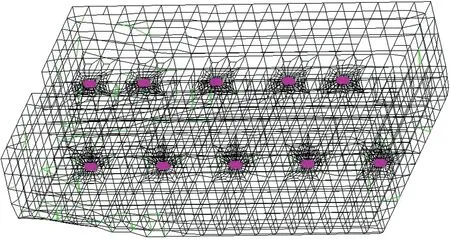
图6 横向强度有限元模型
由于仅考虑横向强度,故模型未对舷侧螺栓进行有限元建模,仅考虑纵舱壁处的甲板/船底的螺栓结构。按照第3 节所述方法(载荷、边界条件、计算衡准),经计算结果如下页图7 所示。
结果分析:螺栓底座应力水平较高,是因其结构局部刚度较大且承担螺栓集中力载荷所致;螺栓应力水平较低,主要因船舶横向局部载荷导致横向分离力较小且垂向的剪力由螺栓底座承担所致。

图7 有限元计算结果
5 结 语
可拆解组合式船舶属于一种新颖设计,现行规范体系中没有适合的方法对其进行强度校核。本文从船体梁基本原理出发,结合CCS 规范提出了科学的、合理可行的船体梁-螺栓强度等效原则,横向结构-螺栓强度等效原则,最终将该理论应用于船舶结构设计,使该项目能够顺利完成,为后续该类船舶设计与审图提供了有益的参考。
