基于CATIA的EPS渐开线蜗轮蜗杆参数化建模及仿真

2019-12-25陈志刚王先声周廷明罗斌默辰星

邵阳学院学报（自然科学版） 2019年6期

陈志刚，王先声，周廷明，罗斌，默辰星

(1．邵阳学院机械与能源工程学院，湖南邵阳，422000；2．株洲易力达机电有限公司，湖南株洲，421000；3．邵阳学院高效动力系统智能制造湖南省重点实验室，湖南邵阳，422000)

电动助力转向系统(electric power steering system,EPS)是新能源汽车的重要组成部分之一，蜗轮蜗杆是电动助力转向系统的关键传动零件。无论是小齿轮助力式转向系统(P-EPS)还是管柱助力式转向系统(C-EPS)，均需要使用蜗轮蜗杆减速机构对助力电机进行减速和增加扭矩，从而提供足够的助力辅助驾驶员进行车辆转向[1]。

现有主流技术，蜗轮蜗杆的模型大多是通过KiSSsoft等齿轮生成器生成，或者利用Creo或Solidworks等软件的齿轮工具箱自动生成。但是，实际的蜗轮蜗杆产品通常有一些独特的技术特征，使用现有的自动生成技术无法自动生成特有特征，用户只能在模型基础上做进一步设计，这样降低了设计效率。因此，对于企业用户而言，迫切需要一种能自动生成特有特征的蜗轮蜗杆三维模型的通用设计方法。

CATIA(computer aided three-dimensional interactive application)是法国达索(Dassault System)公司旗下的CAD/CAE/CAM一体化软件，是世界领先的产品设计和体验解决方案。

刘广武等[2]依据蜗轮滚刀包络加工蜗轮齿面原理，提出了基于CATIA V5平台的ZA蜗轮齿面参数化精确数字建模的方法；孙慧等[3]在UG平台上实现了渐开线蜗轮蜗杆的参数化设计方法，用参数化表达式完成蜗轮蜗杆实体的精确造型；赵迪等[4]对渐开线蜗轮蜗杆的参数化设计进行了简单叙述，并对其装配误差进行了分析。但是，截至目前为止，尚未见到相关文献详细及介绍基于CATIA平台的渐开线蜗轮蜗杆的精确参数化设计，特别是关于渐开线蜗轮参数化设计方法的介绍。

因此，本文利用CATIA软件对电动助力转向器蜗轮蜗杆进行精确的参数化建模，得到可编辑具有特有特征的蜗轮蜗杆参数化模型，能有效提高设计效率，并可用于各类有限元仿真分析。

1 参数化建模

渐开线蜗轮蜗杆的齿形与渐开线圆柱齿轮的齿形一致。图1为EPS蜗轮蜗杆产品图，数据来源于株州易力达机电有限公司研究院提供的EPS蜗轮蜗杆设计图纸，由于图纸数据经过修改，与国标有差异，因此根据表1的数据计算出蜗轮蜗杆各个尺寸数据。

(a)蜗轮产品图(a)Product diagram of worm gear

(b)蜗杆装配产品图(b)Product diagram of worm assembly

表1 蜗轮蜗杆参数表
Table 1 Parameter table of worm gear and worm

产品蜗杆蜗轮类型 ZI型(渐开线型)法向模数/mm 2头数236法向齿形角/(°) 14.5导程角/螺旋线升角/(°) 17.73螺旋方向右旋右旋中心距/mm 45变位系数0-0.18齿厚系数0.250.75

数据来源：株州易力达机电有限公司研究院提供

1.1 渐开线蜗轮建模流程

1.1.1 建立蜗轮参数

根据表1中的数据和设计规范，计算出蜗轮各个尺寸数据，如表2所示。并将表3数据输入CATIA中。

表2 蜗轮公式参数表[5]
Table 2 Parameter table of worm gear formulas[5]

序号名称代号关系式参数1蜗杆头数Z122蜗轮齿数Z2363法向模数Mn24直径系数q6.55齿顶高系数ha∗16顶隙系数c∗0.257齿厚系数Smx∗0.758法向齿形角/(°)αn14.59蜗杆分度圆导程角/(°)γ17.7310实际中心距/mma4511蜗轮齿宽/mmb21412蜗轮外齿直径/mmde28113喉圆半径/mmrg23014齿根圆倒圆角半径/mmr10.515轴向模数/mmMxMn/cos(γ)2.099 716轴向齿形角/(°)αtatan(tan(αn)/cos(γ))15.1917蜗杆分度圆直径/mmd1Mx·q13.64818蜗轮分度圆直径/mmd2Z2·Mx75.5919蜗轮基圆直径/mmdb2d2·cos(αt)72.94920齿顶高/mmhaMn·ha∗221齿根高/mmhfMn·(ha∗+c∗)2.522计算中心距/mma′(d1+d2)/244.61923蜗轮变位系数/mmx2(a-a′)/Mx0.18124蜗轮齿顶圆直径/mmda2d2+2·ha+2·x2·Mx80.35225蜗轮齿根圆直径/mmdf2d2-2·hf+2·x2·Mx71.352

将蜗轮原始数据及公式通过CATIA“零件设计”模块中的“公式”工具输入CATIA中，并建立相应的关系式，其结果如图2所示。

图2 蜗轮参数及公式设置图Fig.2 Parameters and formulas setting diagram of worm gear

图3 渐开线示意图 Fig.3 Involute diagram

渐开线方程的建立，是渐开线蜗轮设计中不可或缺的步骤之一。根据渐开线定义，可知当直线BK沿着蜗轮基圆db2的圆周做纯滚动时，直线BK上任意一点K的轨迹AK即为该圆的渐开线，其中θK为渐开线上K点的展角，单位为弧度[6]。渐开线示意图如图3所示。

本文中需要用到CATIA的法则曲线功能来建立蜗轮的齿廓渐开线，其中渐开线方程如公式(1)[7]所示，转换后如公式(2)所示，并通过 “零件设计”模块中的“fog”工具输入CATIA中，如图4所示。

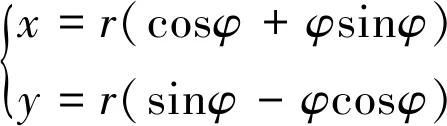
(1)

(2)

图4 法则曲线X设置对话框Fig.4 Dialog box of settings for rule curve X

1.1.2 建立蜗轮几何模型

蜗轮的建模方法一般有两种：一种是直接建模法，直接生成齿轮的齿形；另一种是布尔操作法，通过切除齿轮毛坯上的齿槽来加工齿轮。

本文为保证模型更加精确，根据实际蜗轮加工方法，采用布尔操作法来建立蜗轮模型。首先，利用法则曲线公式生成蜗轮的齿槽轮廓。将齿槽轮廓沿着直径方向平移，得到变位齿槽轮廓，如图5所示。利用“扫掠”命令，将变位齿槽轮廓沿着喉圆进行扫掠，生成蜗轮齿槽曲面，如图6所示。

图5 蜗轮齿槽草图Fig.5 Sketch of worm gear tooth space

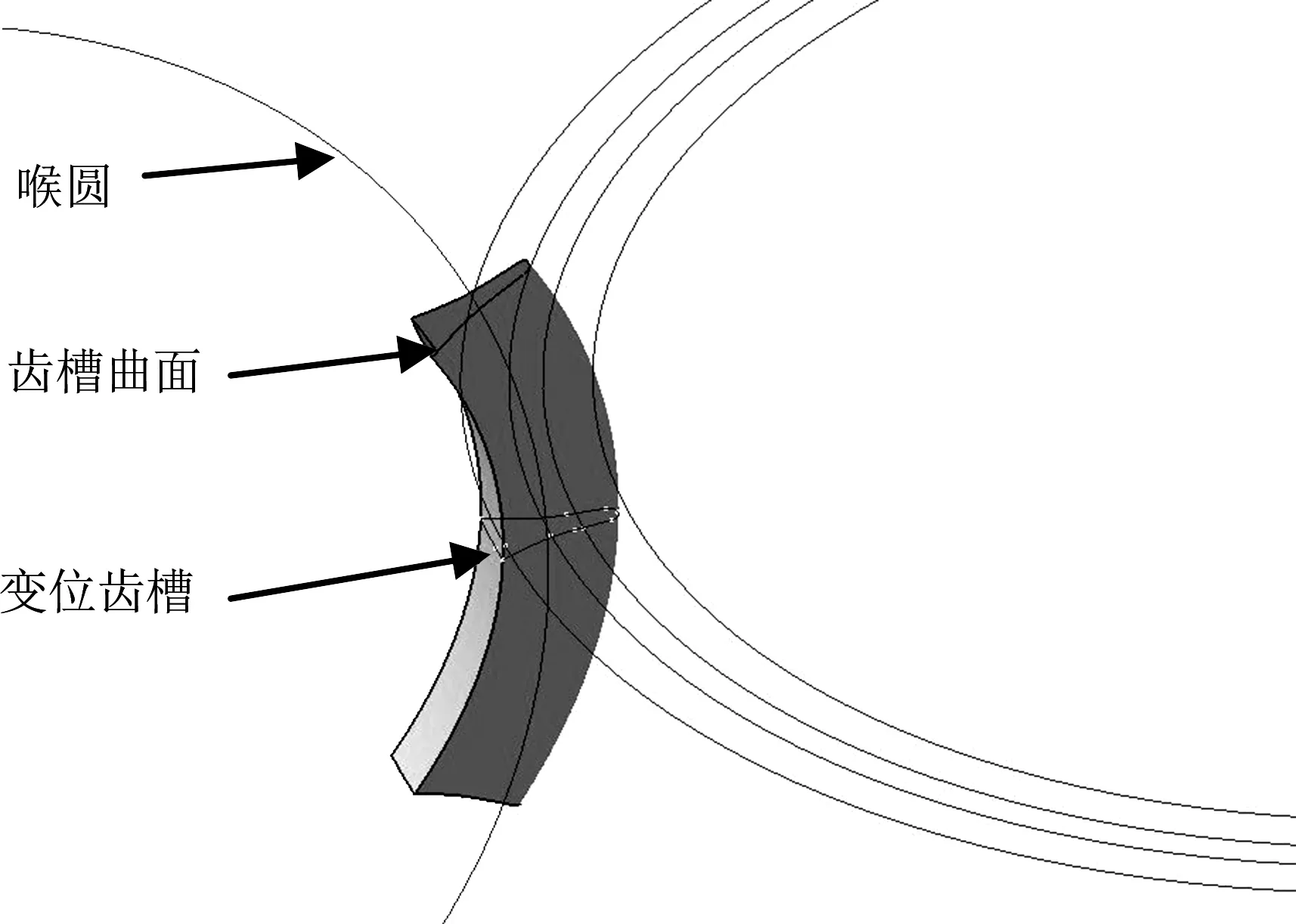
图6 蜗轮齿槽曲面Fig.6 Curved surface of worm gear tooth space

接下来绘制蜗轮外齿轮廓，如图7所示；其中，带“f(x)”符号的数据均为参数化数据，可随着参数改变而改变。

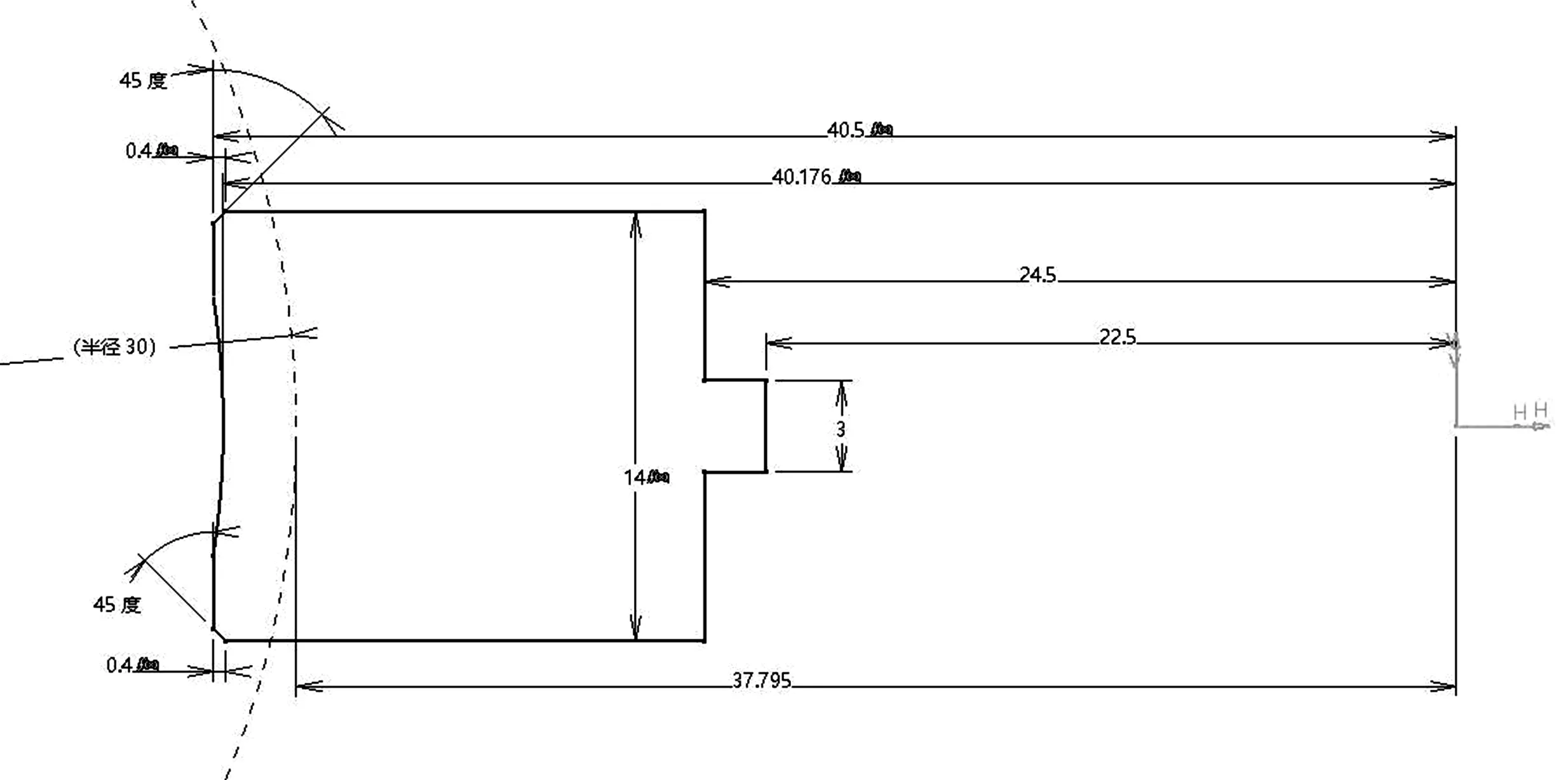
图7 蜗轮外齿轮廓Fig.7 Profile of outer teeth of worm gear

创建旋转体，将蜗轮外齿轮廓草图绕着蜗轮轴线旋转，从而获得蜗轮毛坯模型，如图8所示

图8 蜗轮毛坯Fig.8 Semifinished product of worm gear

创建新的几何体，将扫掠得到的变位齿槽曲面进行封闭，再对当前实体进行阵列，然后通过布尔操作在蜗轮毛坯上切除相交部分，即可完成蜗轮参数化建模，如图9、10所示。

图9 圆形阵列对话框Fig.9 Dialog box of circular array

图10 蜗轮三维模型图Fig.10 3D model diagram of worm gear

1.2 渐开线蜗杆建模流程

1.2.1 建立蜗杆参数

根据表1数据和设计规范，计算出蜗杆各个尺寸数据，如表3所示。并将表3数据输入CATIA中。

表3 蜗杆公式参数表[5]
Table 3 Parameter table of worm formulas[5]

序号名称代号关系式参数1蜗杆头数Z122蜗轮齿数Z2363法向模数Mn24直径系数q6.55齿顶高系数ha∗16顶隙系数c∗0.257齿厚系数Smx∗0.258法向齿形角/(°)αn14.59蜗杆分度圆导程角/(°)γ17.7310实际中心距/mma4511蜗杆齿宽/mmb14812齿根圆倒圆角半径/mmr10.513轴向模数/mmMxMn/cosγ2.099 714轴向齿形角/(°)αtatan(tanαn/cosγ)15.19°15蜗杆分度圆直径/mmd1Mx∗q13.64816蜗轮分度圆直径/mmd2Z2∗Mx75.5917蜗轮基圆直径/mmdb2d2∗cosαt72.94918齿顶高/mmhaMn∗ha∗219齿根高/mmhfMn∗(ha∗+c∗)2.520计算中心距/mma′(d1+d2)/244.61921蜗轮变位系数x2(a-a′)/Mx0.18122蜗杆齿顶圆直径/mmda1d1+2∗ha17.64823蜗轮齿顶圆直径/mmda2d2+2∗ha+2∗x2∗Mx80.35224蜗杆齿根圆直径/mmdf1d1-2∗hf8.64825蜗轮齿根圆直径/mmdf2d2-2∗hf+2∗x2∗Mx71.35226轴向齿距/mmPxMx∗π6.59727蜗杆导程/mmPzZ1∗Px13.193

1.2.2 建立蜗杆几何模型

从渐开线蜗杆的几何性质可知，渐开线蜗杆相当于一个齿数较少，螺旋角较大的渐开线圆柱斜齿轮，因此其端面齿廓是同样是渐开线。

渐开线蜗杆齿槽的绘制与蜗轮大致相同，同样通过布尔操作法来建立蜗杆模型，值得注意的是，蜗杆的渐开线方程并不是用蜗杆的参数进行绘制的，而是利用匹配的蜗轮参数进行绘制，最终生成齿槽如图11所示。

图11 蜗杆齿槽草图Fig.11 Sketch of worm tooth space

在蜗杆齿槽中心平面上沿着蜗杆轴线建立螺旋线与退刀槽引导线，再将蜗杆齿槽沿着曲线进行扫掠，得到蜗杆齿槽曲面，如图12所示。

与蜗轮建模类似，通过布尔操作在蜗轮毛坯上切除相交部分，即可完成蜗杆参数化建模，如图13所示。

图12 蜗杆齿槽曲面Fig.12 Curved surface of worm tooth space

图13 蜗杆三维模型图Fig.13 3D model diagram of worm

2 装配与运动仿真

进入“装配设计”模块，导入蜗轮蜗杆模型文件进行装配，根据装配关系进行约束；然后选择“碰撞”命令，检查蜗轮蜗杆之间有无发生干涉，如图14所示，蜗轮蜗杆之间碰撞类型为“接插件”，没有发生干涉。

再通过测量工具，检测啮合面之间的间隙，如图15所示，重合度介于2和3之间，啮合部位最大总间隙值为0.033 mm，满足装配要求。

图14 碰撞干涉检测Fig.14 Detection of collision and interference

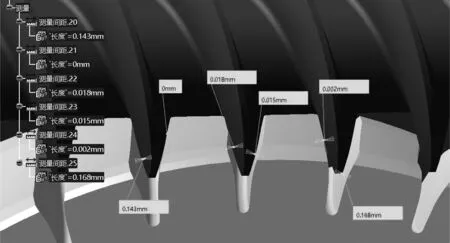
图15 啮合部位间隙值检测Fig.15 Measurement of clearance values of meshing position

进入“DMU运动机构”模块，创建连接副及驱动，进行运动仿真，如图16所示，激活传感器后没有检测到运动干涉。

图16 运动干涉检测Fig.16 Detection of motion interference

3 ANSYS有限元仿真分析

3.1 导入模型

建立蜗轮蜗杆装配体，导入ANSYS Workbench的“静力学分析(Static Structural)”模块中进行处理。

3.2 网格划分

建立蜗轮蜗杆瞬态动力学仿真模型，其中网格划分方式为四面体单元，蜗杆网格单元尺寸控制在1.6 mm，蜗轮网格单元尺寸控制在1.9 mm，中等网格质量，如图17所示。

3.3 边界与初始条件的施加

蜗轮蜗杆进行啮合传动，啮合部位添加摩擦接触，摩擦系数为0.13。将轮毂与蜗轮进行绑定，在轮毂内表面施加一个80 N·m的恒定负载转矩以及约束，释放Y轴旋转自由度，如图18所示，材料为PA46-GF15；蜗杆在轴承端施加固定约束，材料为40 Cr。

3.4 分析结果

经过计算，得到蜗轮蜗杆静力学分析结果，其等效云图如图19所示。

图17 蜗轮蜗杆网格划分结果Fig.17 Results of mesh division of worm gear and worm

图18 蜗轮蜗杆静力学仿真模型Fig.18 Static simulation model of worm gear and worm

(a)蜗轮蜗杆等效应力云图
(a)Equivalent stress contour of worm gear and worm

(b)蜗轮蜗杆等效应变云图(b)Equivalent strain contour of worm gear and worm

(c)蜗杆最大等效应力云图(c)Maximum equivalent stress contour of worm

(d)蜗杆最大应变等效云图(d)Maximum equivalent strain contour of worm

(e)蜗轮最大等效应力云图(e)Maximum equivalent stress contour of worm gear

(f)蜗轮最大等效应变云图
(f)Maximum equivalent strain contour of worm gear

图19等效应力云图及等效应变云图
Fig.19Equivalent stress contours and equivalent strain contours

由于材料不一样，可以发现蜗轮承受的应力普遍小于蜗杆，但是应变量却是远大于蜗杆，因此在设计中对蜗轮的齿厚进行加大是有必要的，以保证蜗轮强度要求。经分析，蜗轮最大应力值为76.309 MPa，产生在齿根过度圆角处，没有超过其材料的屈服强度(97 MPa)；而蜗杆最大应力值为549.35 MPa，也产生在齿根过度圆角处，没有超过其材料屈服强度(785 MPa)，均在安全范围内，满足强度要求。

综上所述，该参数化模型可用于有限元仿真分析，分析表明所选参数下的蜗轮蜗杆最大接触应力能满足强度要求，并可用于实验参考，减少试验费用以及时间，获得更接近实际的分析数据。