一种改进的EKF-SLAM算法

许柏杨，王冬青

（青岛大学 自动化与电气工程学院，青岛 266071）

0 引言

随着现代物流的快速发展，企业对物流系统的自动化与灵活性有着很高的要求，自动导引车（AGV）是一种常见的运输工具。传统的AGV依赖于既定的静态结构化工作环境，它的智能化与灵活性有限，于是人们提出了AGV的同时定位与地图构建（SLAM）来克服这些缺点。目前，解决SLAM问题中的EKF-SLAM，PF-SLAM，FastSLAM及UKF-SLAM算法中，EKFSLAM算法最先被提出、最为流行。张超等人使用改进的Shi-Tomas特征点检测算法进行特征点提取，从而提高SLAM中的地图构建的准确性，但计算复杂度高；贺利乐等人针对移动机器人在未知环境下自主导航时，仅利用单一传感器出现的不能及时定位、构建的地图不精确、鲁棒性不强等问题，提出一种双目视觉与激光雷达信息融合的组合导航方法，但效果并不理想；吴勇等在无迹卡尔曼滤波的基础上提出了一种收缩无迹卡尔曼滤波器，并应于于SLAM问题中，降低了SLAM中的大规模的复杂程度，但并没有解决生成特征图的准确问题；白云汉 将卷积神经网络的算法与SLAM算法融合，提高了系统的定位精度，但计算的复杂度较高。然而，在解决移动机器人的定位与地图构建问题的过程中，传统扩展卡尔曼滤波的计算复杂度高，生成的特征图准确性不足，并且通常与导航分离，基于此，在本文中提出了IEKF-SLAM算法并且使其与D*导航算法结合，通过将机器人的系统参数附加到EKF SLAM的状态向量中，在执行预测和更新EKF SLAM的状态时，对附加系统参数的状态向量进行估计，消除内部传感器引起的误差，从而提高特征图的准确性，实现AGV的完整状态估计，并且针对EKF-SLAM算法计算复杂度高的问题，提出了相关的算法，使AGV在动态和非结构化的环境中能够自动定位并准确跟踪路径，提高了系统的工作效率和系统灵活性，降低施工成本。

1 运动学模型

如图1所示AGV运动模型，具有不同速度的四轮结构。两个驱动轮位于车身对称的位置，两个从动轮安装在垂直于车身两侧的位置，该车辆由两个驱动轮驱动。

假定质心与所述AGV的几何中心点相同。在一个采样周期中，AGV的运动可以被近似为一个弧。在相邻的采样时间的位置矢量用x，y，θ和x(k+1)，y（k+1），θ（k+1）表示，如图1所示。

当采样周期为Ts，则AGV运动学方程如下：

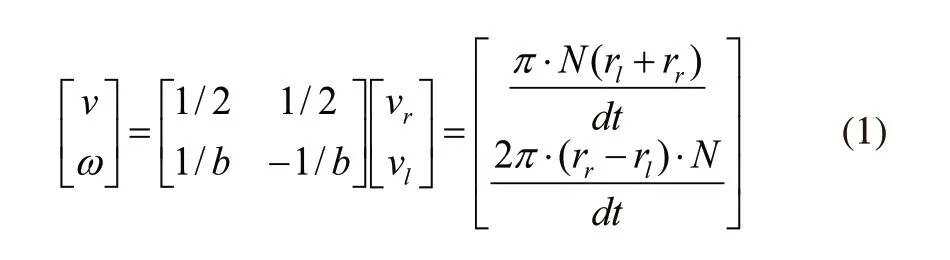
其中符号说明如下：

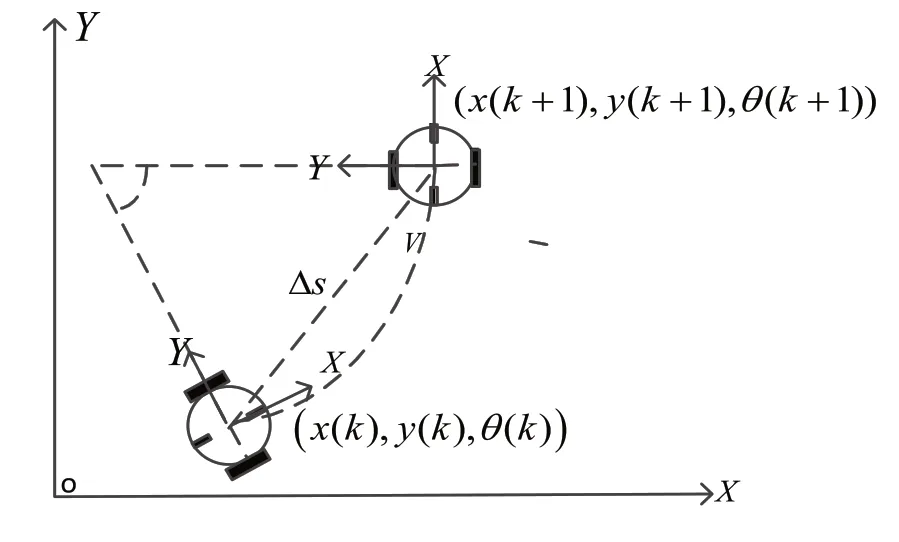
图1 AGV的运动模型

v：AGV的质心速度

ω：AGV质心的角速度

b：两个驱动轮之间的距离

vl，vr：左右驱动轮的速度

rl，rr：左右车轮的标称直径

rl*，rr*：左右车轮的实际直径

∆s：AGV在一次取样中的位移

∆θ：AGV的偏转角度

T：采样周期。

（xv（i），yv（i），θ（i））T：第i时刻的AGV位置向量

设δl，δr为左右车轮直径的系统参数，δb为轮距的系统参数，则左右车轮的实际直径为：

两个驱动轮间的实际距离为：

因此，实际左右驱动轮的速度为：

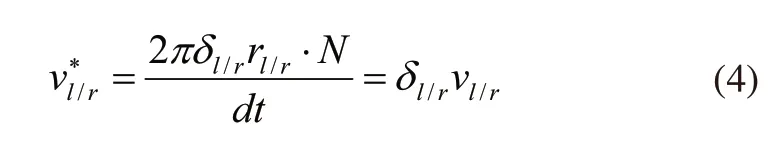
因此，AGV的实际速度为：

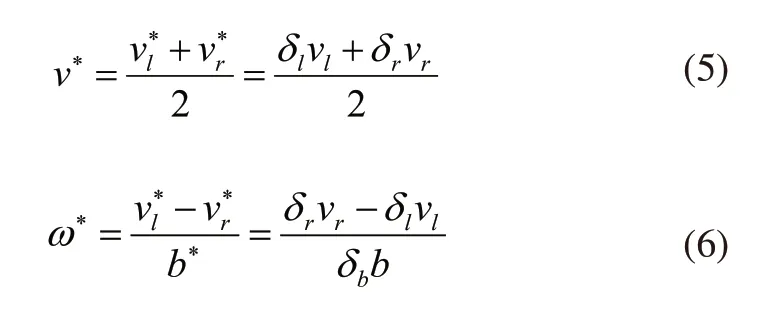
AGV位移和角度表示为：

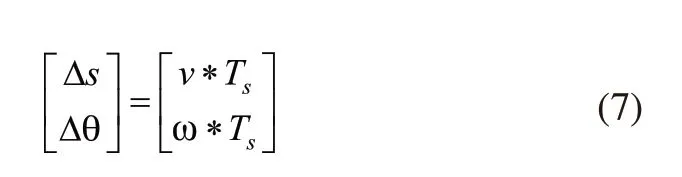
AGV位置方程为：

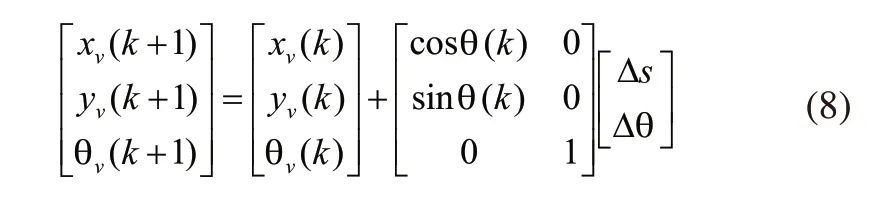
2 IEKF SLAM

基于EKF-SLAM的方法对系统的运动模型和传感器的噪声模型是非常敏感的，因此，我们需要一个准确的模型，但是，在真实的机器人系统中很难找到准确的运动模型和噪声模型，除此之外，由于EKF通常有一个假设的高斯白噪声，如果有一个有色噪声或系统偏差，那么无法保证特征提取的准确性，例如，如果车辆左右车轮的距离或车轮的半径不精确，将会造成系统的估计误差不断增加，从而准确性大大降低。

我们可以通过估计系统参数δl，δr和δb的方法来减少机器人内部里程计的误差。在IEKF-SLAM中，系统参数将增加到系统的状态向量中作为其元素，然后系统参数，机器人的状态以及观察特征的位置将会通过卡尔曼滤波算法的步骤被更新，更新后的系统参数将会减少在预测过程中的里程计的测量误差，从而使EKFSLAM方法的特征地图更加精确。具体的过程如下。

车辆在K时刻的整体状态x（k）由车辆在K时刻的位置状态Xv（k）=[xv（k），yv（k），θv（k）]T和地标的位置Xm（k）=（x1，y1，x2，y2，...，xm，ym）T，以及车辆的系统误差的参数向量Xω=[δl，δr，δb]T组成，（x，y）是第j个地标的位置。即：

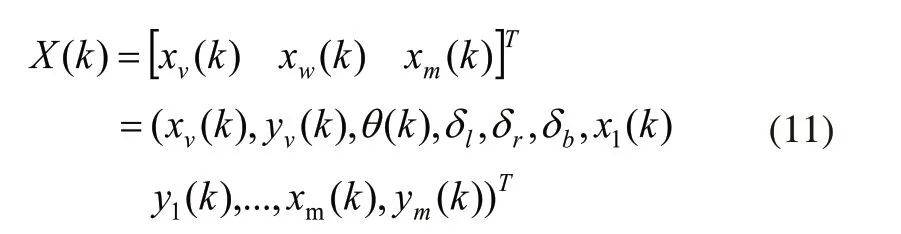
系统相应的协方差矩阵为：

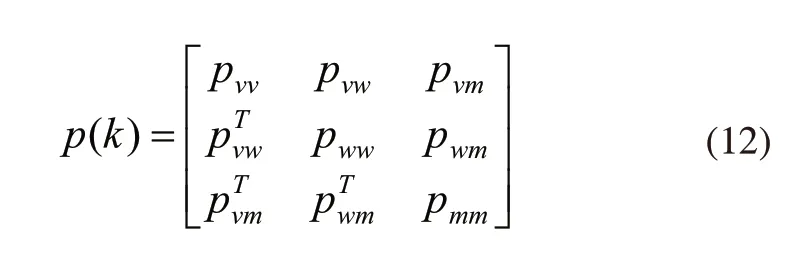
AGV运动过程模型如图2所示，暗区是估计的信息，而浅色区域是实际信息；xk是AGV在k时刻的状态，每个时刻状态的数据构成了AGV的轨迹；Zk是在k时刻观察到第j个地标；uk是在（k-1）时刻的控制输入。

AGV从不确定的初始位置移动逐步获得估计的环境地图，并估算AGV自身的位姿。同步定位和创建地图可以分为四个步骤。

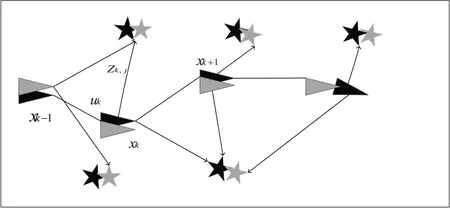
图2 移动过程中AGV的SLAM模型

2.1 预测阶段

在k时刻，设具有系统参数误差的状态向量为Xw（k）=[δl，δr，δb]T，系统整体状态如下：

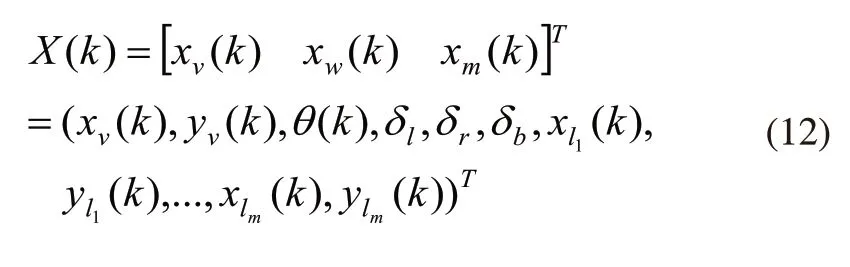
基于EKF-SLAM方法描述车辆的运动模型为：

其中，W（k）表示过程噪声，在此我们忽略掉除系统参数误差外的其他噪声。

因此，车辆在 k 时刻的预测运动学方程为：

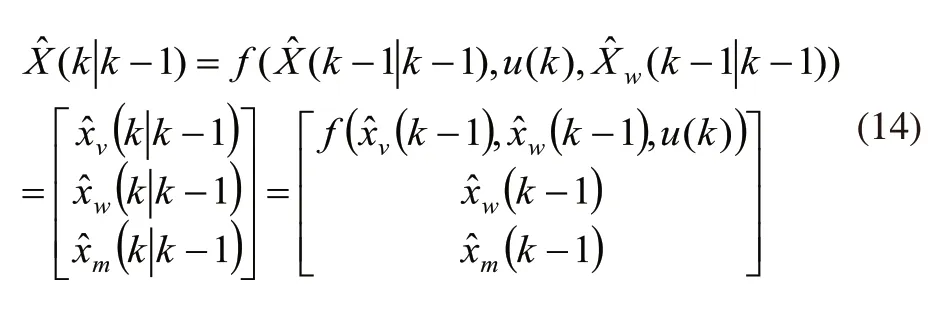
其中，考虑到系统参数的AGV运动模型为：

协方差预测为：

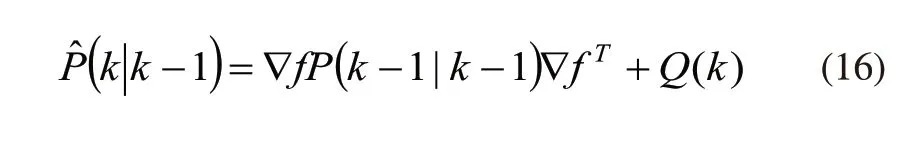
其中，Q是表示不确定性的协方差控制向量；▽f为车辆状态(13)的雅可比矩阵：

2.2 数据关联

在移动机器人SLAM中，数据关联用来建立观测量与地图中地标的关系，并且每一个观测量对应一个地图中的地标，在（k+1）次，AGV获得新的地标观测量，对于观测到的地标，车辆将更新地标位置（步骤3）；否则进行状态扩充（步骤4）。目前有一些广泛使用的数据关联算法，例如最近邻方法（NNM），概率数据关联（PDA）算法等。

2.3 更新阶段

在k时刻，根据数据关联算法AGV获得观察数据，与观察数据匹配的地标j的估计位置是。因此，第j个地标的观测量是：

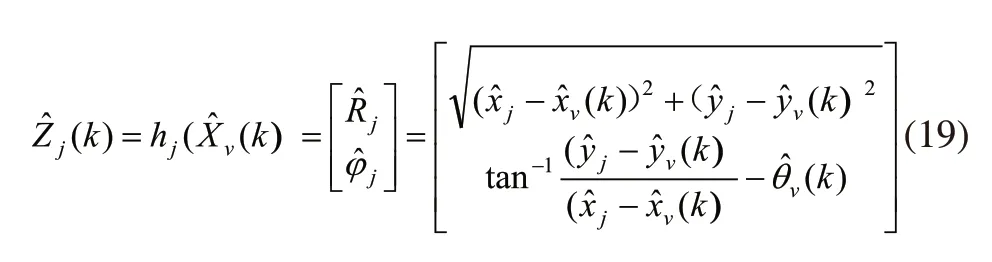
其中，R表示地标的距离，j是观察到的地标相对于AGV的角度，Zj表示第j个地标的观测量。

对测量值线性化并获得雅可比矩阵：

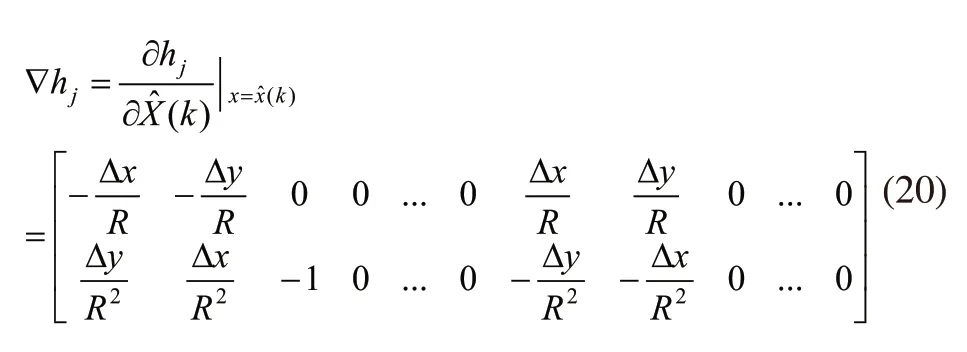
Rk是观察误差的协方差矩阵：

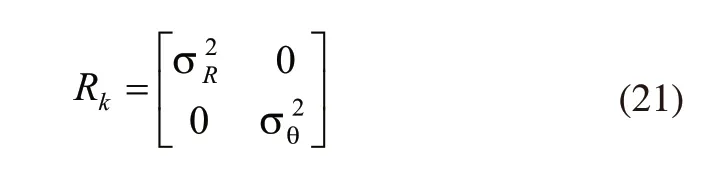
根据扩展卡尔曼滤波我们可以获得卡尔曼增益矩阵：

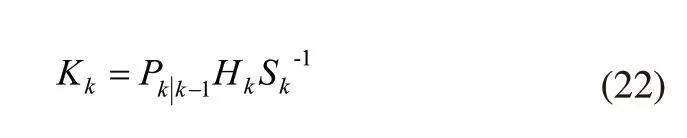
残差协方差：

然后通过式(21)、式(22)分别获得机器人更新的状态向量和协方差：

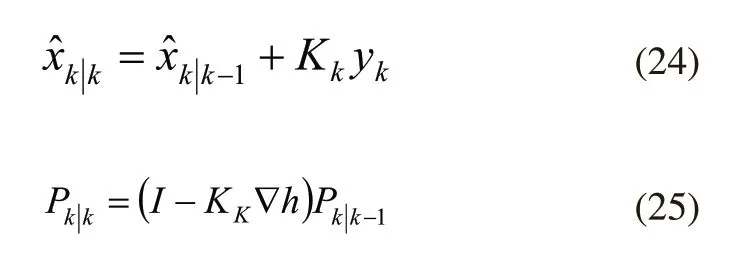
2.4 状态扩充

随着车辆的移动，通过数据关联，新的地标将出现在AGV的观察范围内。因此，它有必要通过在地图中添加新的地标来更新（k+1）时刻的状态。

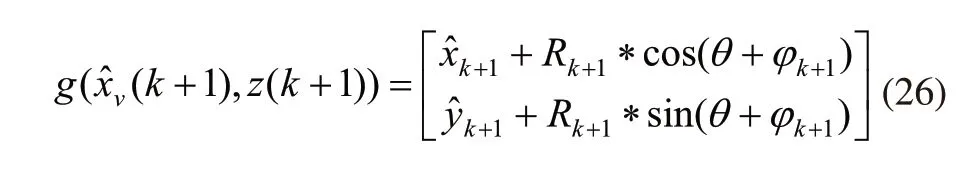
更新后，系统状态向量为：

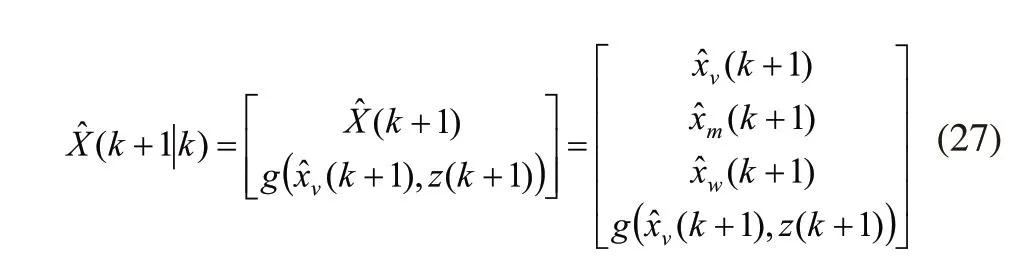
至于扩充的协方差矩阵，首先，分别计算在新的地标下的机器人位姿的雅可比矩阵和观测量的雅克比矩阵：

然后通过在上一时刻的协方差矩阵和新地标的雅可比矩阵得到扩充协方差矩阵：

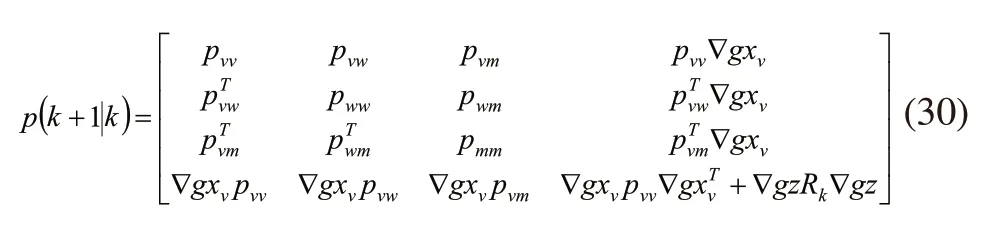
2.5 计算的复杂性

由于协方差矩阵的更新，EKF-SLAM的计算复杂度为O（N2），其中N是环境中的地标数量。这限制了在大规模环境等特征数量大的场合中使用EKF。因此，很多不同的改进算法被提出，其中，主要是利用分区更新和子映射的方法降低复杂性。分区更新的方法是把传感器的更新速率限制在一个小的局部区域，使它以一个更低的频率更新整个地图，从而减少计算的负担。目前，分区更新的改进方法有很多，例如压缩EKF（CEKF）[13]，延迟更新算法[14]等。子映射方法是将总区域划分为多个子区域，每个子区域都有和全局坐标相关联的局部坐标，这样预测和更新的过程就会在子图中较少的地标执行，减少了计算负担。目前，子映射的改进方法也有很多，例如解耦随机映射（DSM）算法[15]，局部地图排序算法[16]。

3 D＊算法

在本文中，由于Dijstra算法不适用于在动态环境下，因此采用D*算法用于AGV的最短路径跟踪。其具体的方法是：

1）先用Dijstra算法从目标节点G向起始节点搜索。储存路网中目标点到各个节点的最短路和该位置到目标点的实际值h，k（k为所有变化h之中最小的值）

2）机器人沿最短路开始移动，在移动的下一节点没有变化时，无需计算，利用上一步Dijstra计算出的最短路信息从出发点向后追述即可，当在Y点探测到下一节点X状态发生改变，如堵塞。机器人首先调整自己在当前位置Y到目标点G的实际值h（Y），h（Y）=X到Y的新权值c（X，Y）+X的原实际值h（X）X为下一节点（到目标点方向Y-＞X-＞G），Y是当前点。k值取h值变化前后的最小。

3）用A*或其他算法计算Y的字节a的值，这里假设用A*算法，遍历Y的子节点，点放入CLOSE，调整Y的子节点a的h值，h（a）=h（Y）+Y到子节点a的权重C（Y，a），比较a点是否存在于OPEN和CLOSE中。如果a的值小于OPEN以及CLOSE表中的a值，则更新OPEN和CLOSE表中的a值。

4）利用第一步Dijkstra算法计算出a点到目标点的最短路径，重复上述操作，完成最短路径的跟踪。

4 仿真与结果分析

为了验证具有系统参数估计的IEKF-SLAM具有更好的操作性能，我们进行了仿真实验，仿真实验室在MatlabR2014a平台上进行的，首先X轴坐标为-10m～20m、Y轴坐标为-25m～20m，范围内产生若干个环境特征，假设机器人和目标均为理想模型，目标的实际运行轨迹是不规则的，仿真实验总体如图3所示。

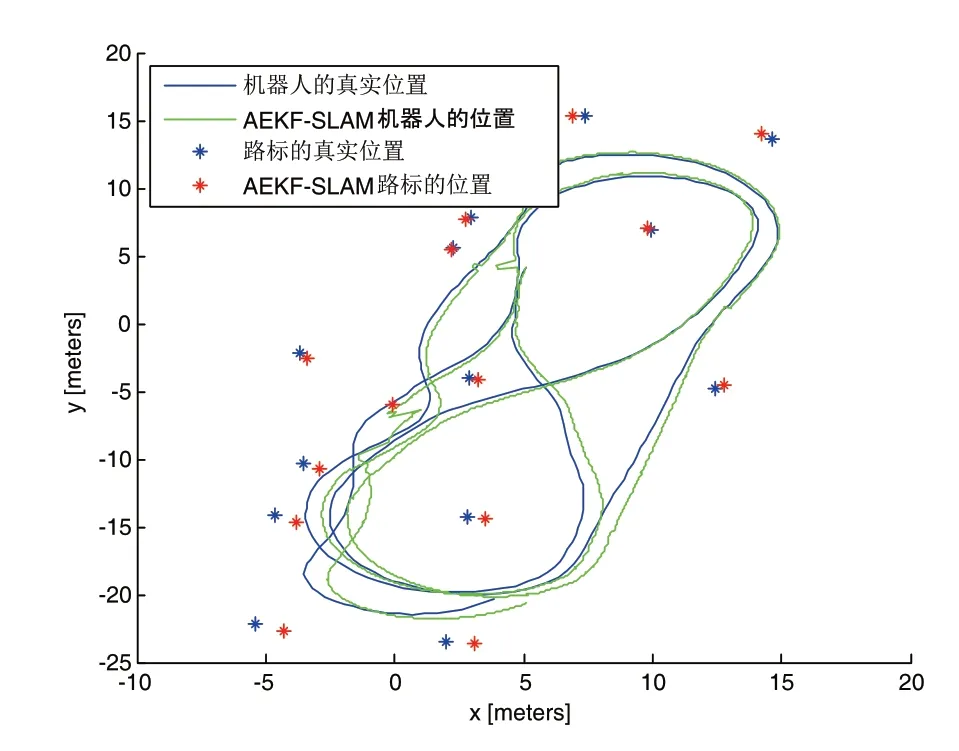
图3 IEKF-SLAM仿真效果图

图3的结果表明，增强的扩展卡尔曼滤波算法使AGV在跟踪路径上有更好的效果。

图4 在X轴上的路标位置误差

图4和图5显示了机器人的实际路标位置和测量路标位置的均方根误差，从仿真结果中我们得出车辆在X轴上的路标位置均方根误差为22.5m，在Y轴上的路标位置均方根误差为6m。

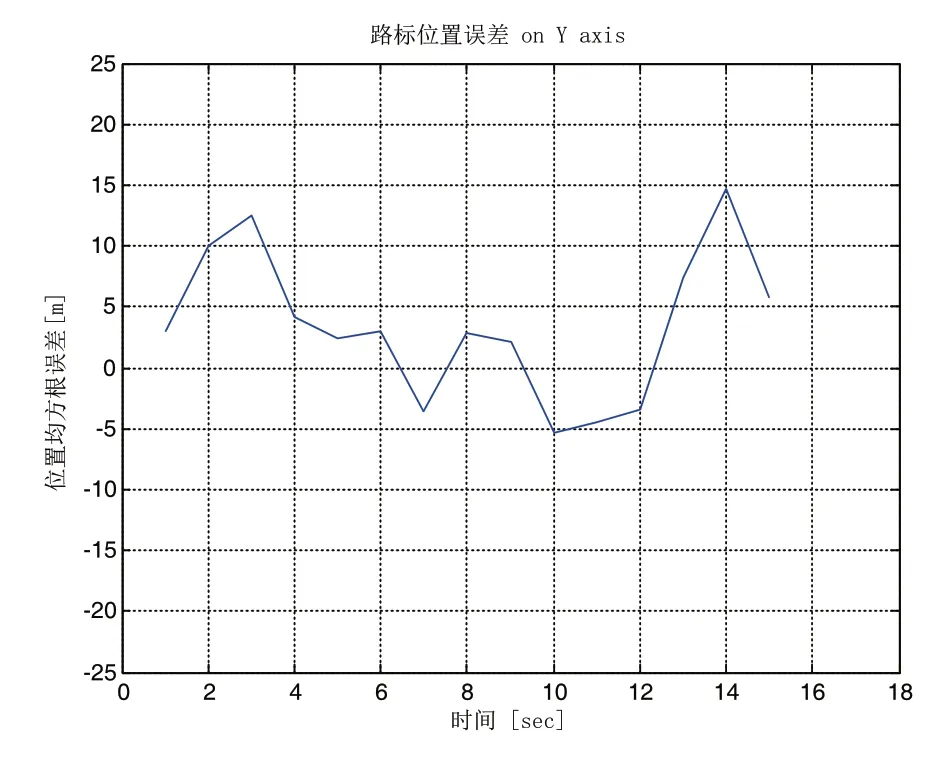
图5 在Y轴上的路标位置误差

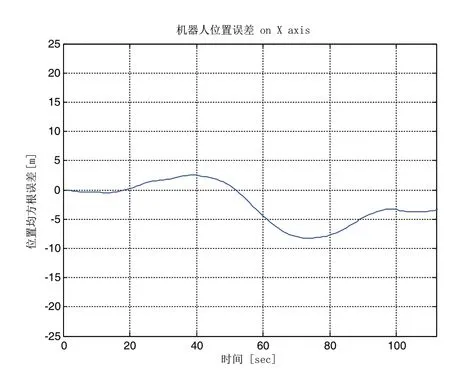
图6 机器人在X轴上的位置误差

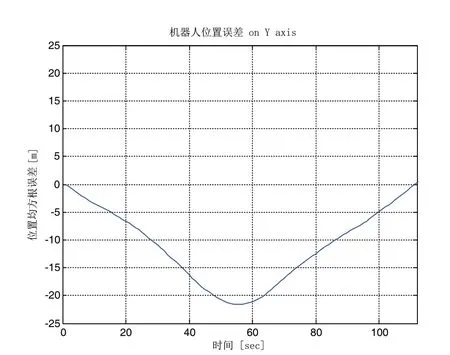
图7 机器人在Y轴上的位置误差

图6和图7分别表明机器人在X轴和Y轴的位置均方根误差。从仿真结果得，机器人在X轴上的位置均方根误差为-4m，在Y轴上的位置均方根误差为0.9m。

5 结论

在本文中，我们针对扩展卡尔曼滤波算法在大范围环境等特征数量较大的场合中计算复杂度高，并且生成的特征图准确性不足的问题，提出了IEKF-SLAM方法，在IEKF-SLAM中，我们将机器人的系统参数附加到EKF-SLAM的状态向量中，在执行预测和更新EKF SLAM的状态时，对附加系统参数的状态向量进行估计，提高了EKF-SLAM的生成特征图的准确性，并提出了一些减少计算复杂性的方法，除此之外，结合了D*导航算法。通过仿真的实验结果我们可以看出，采用对系统参数估计的增强扩展卡尔曼滤波的机器人在生成的特征图方面有更好的准确性，这种方法提高了工作效率，增强了系统的灵活性。