基于对数正态分布的腐蚀损伤预测方法

2019-12-25王强钟勇吴帅苏艳

装备环境工程 2019年11期

王强，钟勇，吴帅，苏艳

（1. 成都飞机设计研究所，成都 610091；2. 西南技术工程研究所，重庆 400039）

铝合金由于比强度、比刚度高和在常规环境下具有良好的稳定性，在现役飞机结构中获得了广泛的应用，特别是在一些关键承力结构中大量使用。铝合金在环境的腐蚀介质的作用下易发生腐蚀，从而影响飞行安全。迄今为止，我国军机的重大腐蚀故障主要发生在铝合金结构中[1]。孔蚀发生在腐蚀初始阶段，针对铝合金孔蚀发展情况进行研究，可为腐蚀早期防护与控制，以及外场飞机经济修理提供支撑。已有文献[2-4]针对飞机蚀坑深度和蚀坑面积数据，分别采用威布尔分布、对数正态分布、Gumbell 第一极值分布、Logistic 模型和Weibull 分布进行对比研究，验证了蚀坑深度和面积随时间呈指数关系，而在蚀坑发展模型研究方面的报道还相对较少。文中通过分析飞机蚀坑深度、体积和面积发展规律，建立了基于对数正态分布的腐蚀损伤预测模型。

1 分布特征统计

1.1 数据整理

文献[2,5]给出了5 个不同日历年限的某飞机铝合金翼梁缘条腐蚀数据，见表1。文中基于此数据开展腐蚀损伤规律研究。

1.2 腐蚀损伤

假设蚀坑开口面积形状为椭圆形，体积为半椭球形，则体积计算公式为：

开口面积计算公式为：

式中：a 代表长度；b 代表宽度；d 代表深度；V代表体积；S 代表面积。据此可计算出每个日历年所统计的17 个蚀坑的体积和面积。

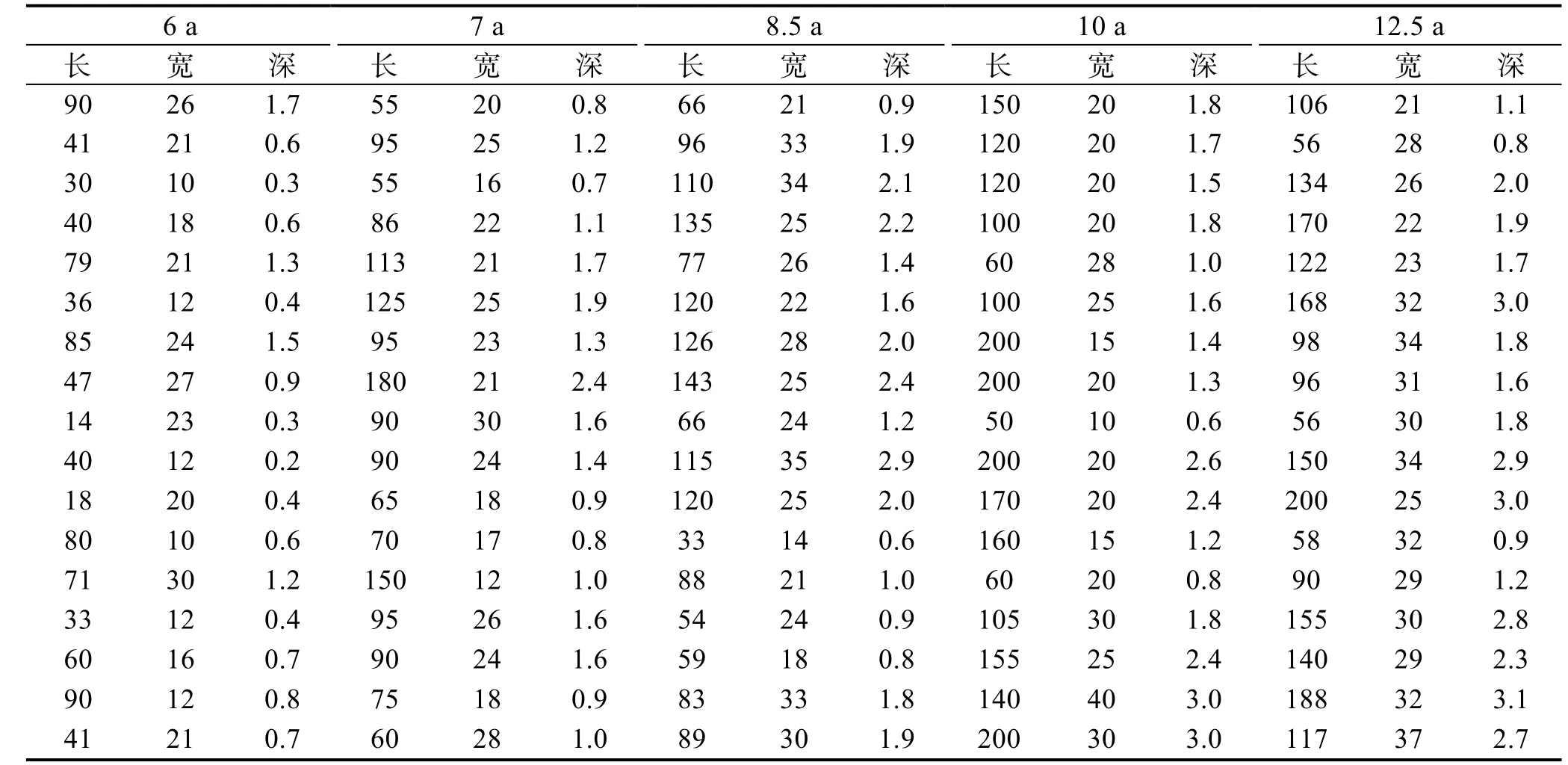
表1 不同日历年限的蚀坑尺寸值 mm

1.3 腐蚀损伤分布特性

将蚀坑深度di(i=1,…,17)、蚀坑体积Vi(i=1, …,17)及蚀坑面积Si(i=1, …,17)变量从小到大排序，则其对应的概率均为Pi=i/18[6]。

假设蚀坑深度、蚀坑体积、蚀坑面积服从对数正态分布，对数正态自变量x 与标准正态分布分位点upi有如下关系：

以第6 年腐蚀数据为例，统计结果见表2。

1.4 分布参数估计

将历年的腐蚀数据(upi, lg xi)(i=1,…,17)绘于图1，并采用概率坐标回归方法[7]估计得到各日历年腐蚀损伤特征量的对数正态分布参数，见表3。根据参数估计的结果，第6 年的腐蚀深度、体积和面积的分布如图2 所示。

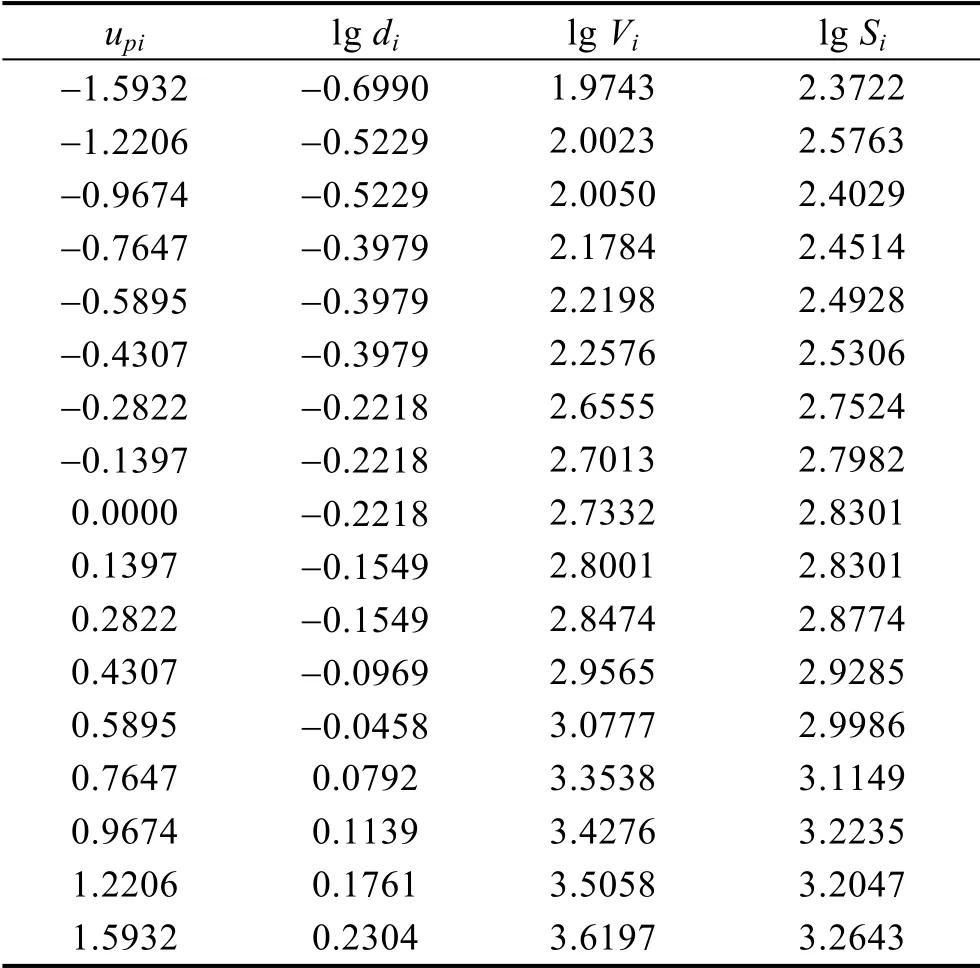
表2 第6 年的腐蚀数据整理

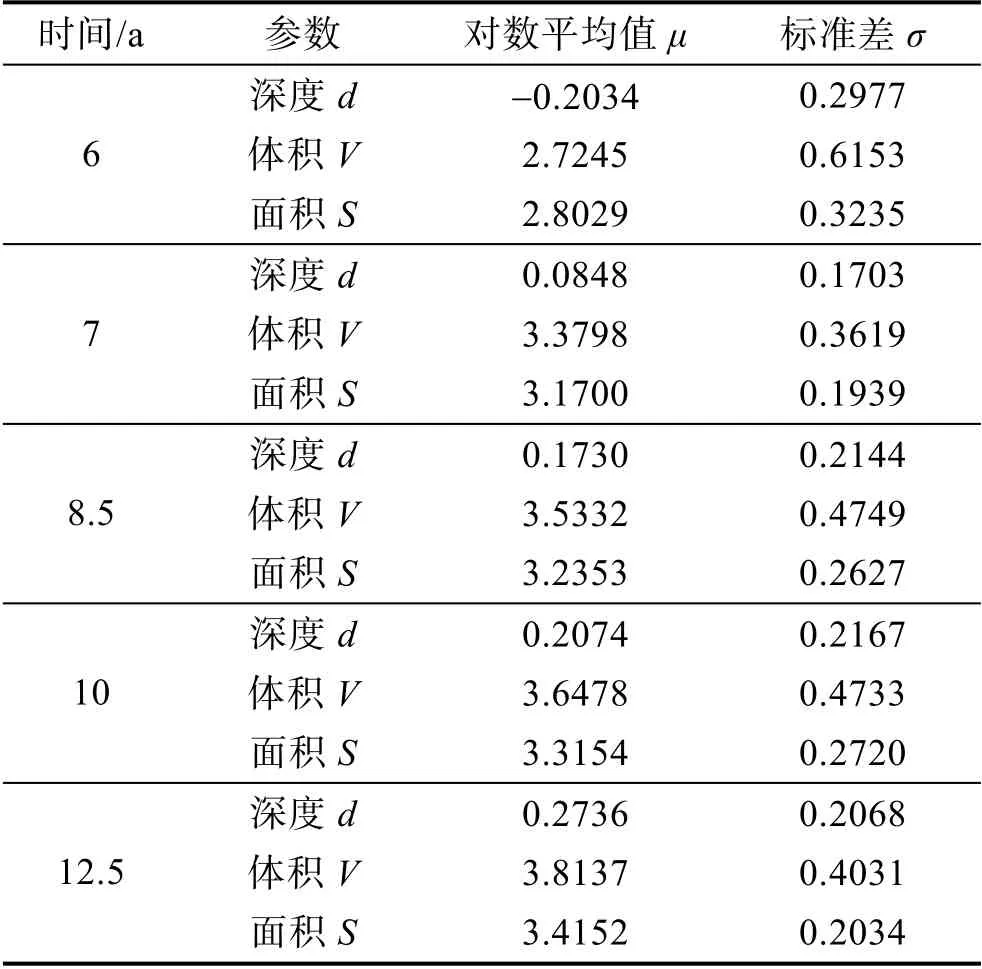
表3 分布参数估计

1.5 假设检验

采用相关系数检验法对该分布进行检验[8]，记(upi, lg xi)(i=1,…,17)为(xi,yi)。根据样本观测数据(xi,yi)(i=1,2,…,17)，针对一元线性回归直线方程为：

令：

此统计量称为相关系数。其中：

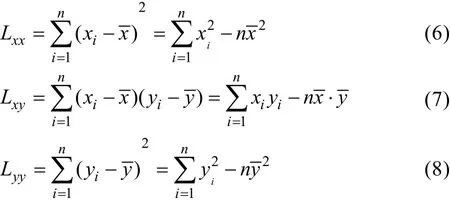
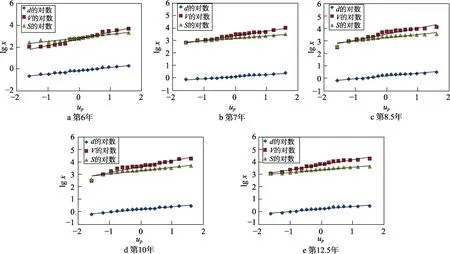
图1 分布参数估计

图2 第6 年腐蚀损伤特征量分布

对于给定的显著性水平α，查相关系数临界值表，可得临界值rα(n-2)。当计算出各分布的r 大于rα(n-2)时，表明在显著性水平α 下，x 与y 服从线性关系。

取显著水平α=0.05，查相关系数检验表，r0.05(15)=0.482，通过式（4）计算得各r 见表4。显然深度d、体积V 及体积S 与upi在显著水平α=0.05 下满足式（3）的线性关系，则可接受深度d、体积V 及体积S 服从对数正态分布的假设。

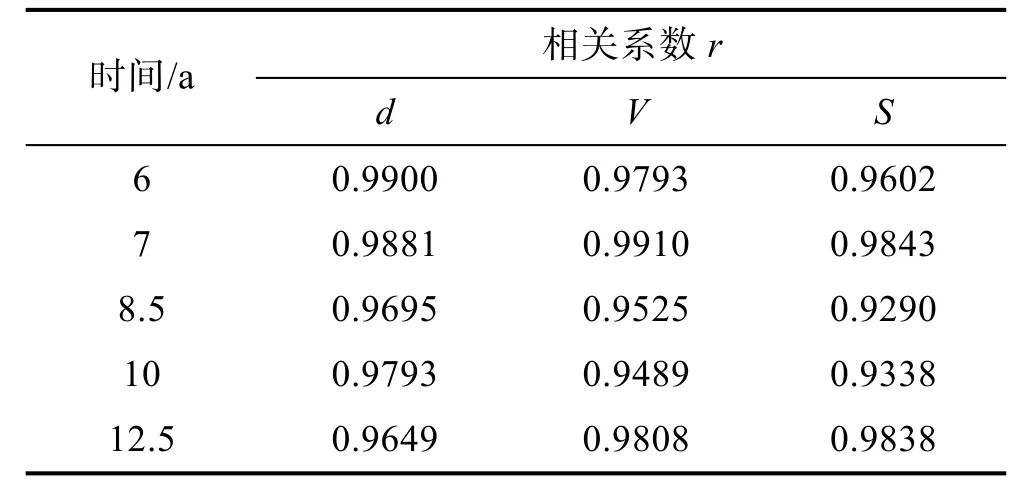
表4 各日历年腐蚀损伤特征量与upi 相关系数

2 腐蚀损伤扩展预测模型

通过6～10 年的各参数分布，计算得到50%、90%和95%三种可靠度下的深度、体积、面积取值，见表5。

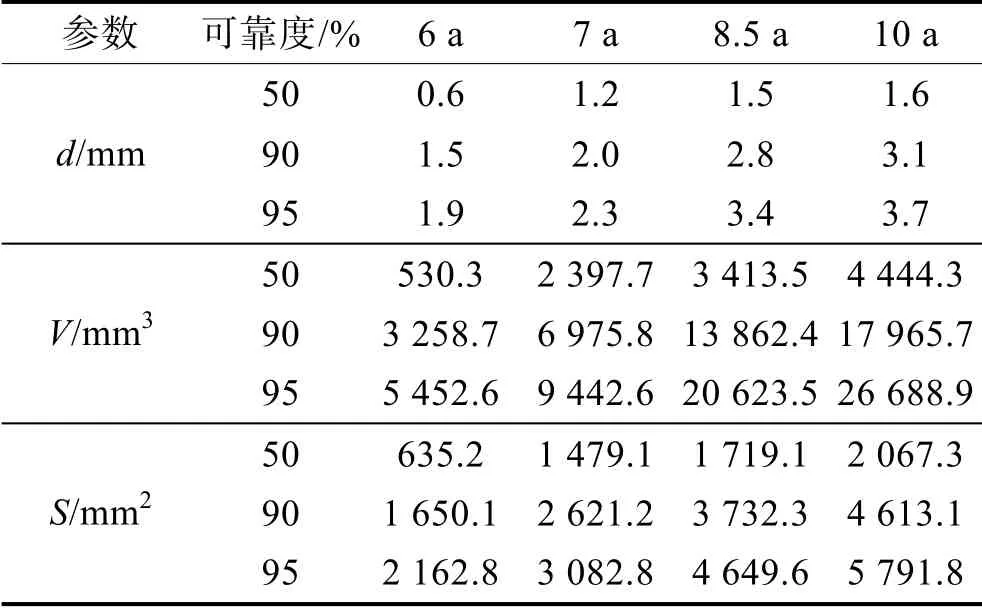
表5 三种可靠度下的参数值

以6～10 年的腐蚀数据为基础，建立腐蚀损伤预测模型。

蚀坑深度预测模型：

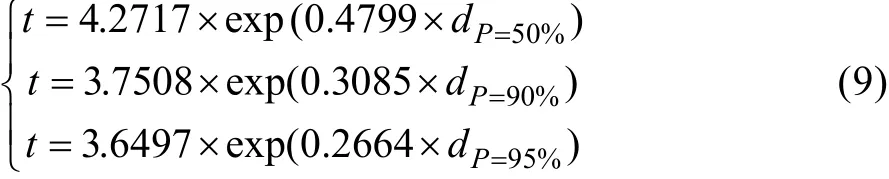
蚀坑体积预测模型：

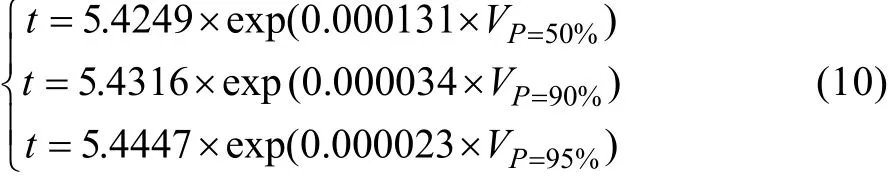
蚀坑面积预测模型：

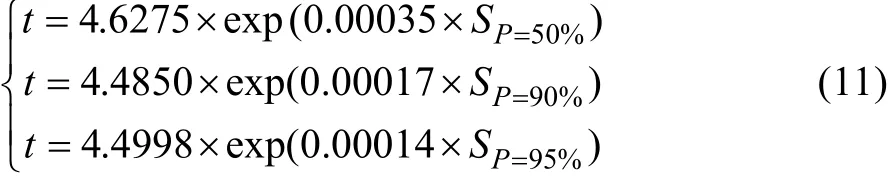
使用12.5 年的数据对所建模型精度进行验证，结果见表6。

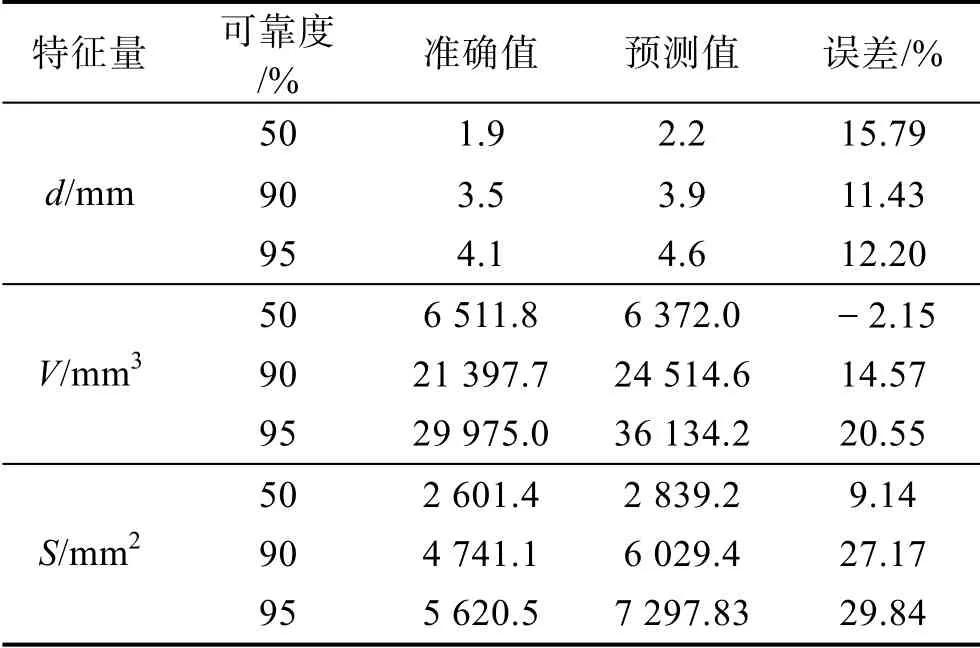
表6 模型预测精度验证

结构基材的腐蚀发生在涂层失效之后[9]，根据式（9）—（11）可知：在可靠度为50%时，根据深度模型计算出的涂层失效时间为4.3 年，根据腐蚀体积反推的涂层失效时间为5.4 年，根据面积失效反推得到的涂层失效时间为4.6 年。涂层体系和服役环境的差异，会导致涂层的失效时间存在差异，文中方法反推出的涂层失效时间，介于文献[4]的2.5 年和文献[10]的12 年之间。