基于气囊缓冲的某火箭炮着陆冲击分析
2019-12-25李强于存贵秦予铮
李强,于存贵,秦予铮
(南京理工大学 机械工程学院,南京 210094)
在现代战争条件下,空降作战以其机动性和突然 性的特点被广泛采用。我国幅员辽阔、地形复杂,一旦局部发生冲突事件,拥有重型装备的空降兵如虎添翼,是解决危机的重要力量[1]。火箭炮具有杀伤面积大、机动性强、成本较低等特点,十分符合现代战争的需求,因而也成为各国空降兵的首选压制武器[2]。在以往的火箭炮空投实践中,由于带弹空投,火箭弹的冲击加速度过大,安全性得不到保证。采取将火箭炮与发射箱(含火箭弹)分开投放的方式,空投完成后,将火箭炮与发射箱进行组装,投入作战,这大大增加了火箭炮的作战准备时间。
目前,火箭炮空投常用的缓冲方式是在火箭炮运载车底部与空投货台之间增加泡沫缓冲装置,但这种方法多受到空投载机货舱高度和空投系统空投质量的限制,有一定的局限性。缓冲气囊以其质量轻、折叠性能好、成本低廉等独特优势,成为重装空投防护、无人机回收、航天器软着陆领域的一个热点研究方向[3-4]。
近年来,国内对空投着陆冲击方面做了大量的研究。郝贵祥利用有限元方法对空降车着陆缓冲过程进行了仿真分析,通过实验数据对比,验证了仿真结果的正确性。卫剑征依据NASA“猎户座”缓冲着陆器的缩比模型,分别研究了缓冲着陆器正碰、侧碰对缓冲气囊压力、着陆器加速度和运动的影响,并与文献进行对比验证。计算结果表明,数值模拟具有正确性。
文中利用有限元软件HYPERMESH 建立某火箭炮-气囊系统有限元模型,基于显式动力学理论,在LS-DYNA 求解器中仿真火箭炮带弹空投着陆缓冲过程,分析火箭弹着陆冲击的安全性。
1 火箭炮-气囊系统空投过程
缓冲气囊在地面折叠成较小的体积,通过支架安装在货台的底部[5]。火箭炮-气囊系统空投过程可分为以下三个步骤。
1)装备在出舱下落过程中,降落伞打开,同时空气通过气囊下端进气孔完成气囊的充气展开。
2)当气囊系统以一定的速度触地后,降落伞脱离,气囊进气孔与地面接触而封闭,装备压缩气囊产生内外压力差,使得系统减速,起到缓冲作用。
3)气囊内压不断增大,达到排气孔开启压强时,排气孔打开,气囊开始向外排出气体,装备继续减速,直至完成整个着陆缓冲过程[6]。
其中,第一步为自充气式缓冲气囊下落充气过程,第二步、第三步为火箭炮-气囊系统着陆缓冲过程。
2 基本控制方程及算法
碰撞是一个复杂的动态过程,接触和冲击载荷影响着碰撞的全过程,系统具有几何非线性和材料非线性等多种非线性[7-8]。因此,对于这一类计算大多采用显式积分算法。在显式有限元算法中,假设当前时步为第n 步,则碰撞运动方程可表示为:
式中:M 为结构的质量矩阵;C 为结构的阻尼矩阵;K 为结构的刚度矩阵;为外界作用力矢量;an为时步n 时的加速度;vn为时步n 时的速度; dn为时步n 时的位移。
式(1)可被改写成:

若M 为对角矩阵,则它的逆矩阵为三角矩阵,其矩阵方程为:

式(4)对时间积分可得到速度iv ,再次积分得到位移 di。这里采用中心差分的显式格式来进行时间积分,中心差分的显式格式为:
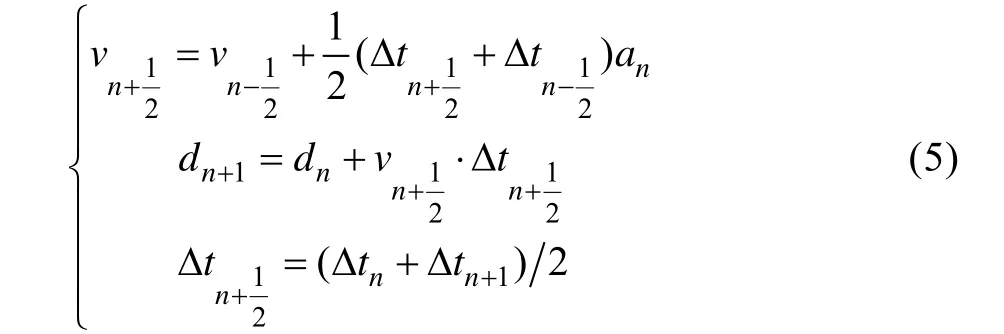
应用显式中心差分法求解碰撞问题时,一个特别值得注意的问题就是时间步长的选取。因为中心差分法是有稳定条件的,其时间步长不能超过临界时间步长[9]。实际应用中常以有限单元网格的特征长度除以应力波速来近似临界时间步长,即:

式中: Δtcr为临界时间步长;cL 为有限单元网格的特征长度;C 为应力波速。
3 有限元仿真模型的建立
火箭炮主要包括运载体、火力系统、火控系统等,全炮结构复杂,因此有必要对其进行适当的简化。建立有限元模型时将运载车的发动机、传动系统、制动系统、火控系统等简化为质量点耦合在车架上,同时保证模型的质量分布与真实的火箭炮尽可能接近。

图1 火箭炮-气囊系统有限元模型
3.1 气囊建模假设
模型采用以下假设对气囊进行建模:空投装备的缓冲完全由气囊产生,不考虑气动阻力;着陆缓冲过程中,空气仅从排气孔流出,即气囊壁不漏气;气囊内各处压力始终是均一的而且气囊内气体是理想绝热的。
3.2 部件简化与单元类型
将几何模型导入到前处理软件HYPERMESH 中进行几何清理。在有限元模型建立的过程中,使网格的外形比、网格变形、单元翘曲度尽可能达到理想状态。对于模型中的一些细节特征,如小孔、圆角、尖锐的过渡区域等进行处理,避免畸形网格的出现,使划分的网格保持连续性[10]。
发射箱分为发射箱箱体、定向器、火箭弹三个部分。箱体和定向器均为薄壁结构,采用壳单元划分网格;火箭弹主要关心弹体着陆时的冲击加速度,对受力情况不作分析。因此采用壳单元划分网格,通过调整弹体壳单元厚度与添加质量单元的方法,使其总质量及重心位置与实弹符合。车架、底架、回转体、起落架、气囊、轮胎、轮毂均为薄壁结构,采用四边形壳单元进行网格划分。在选择壳单元特性时,对轮胎与气囊选用Belytschko-Tsay Membrane 单元算法,对车架、底架、回转体、起落架、发射箱、定向器、火箭弹、轮毂采用Belytschko-Tsay 单元算法。
3.3 材料模型的选择
车架、底架、回转体、起落架、发射箱、火箭弹为弹塑性材料,选用LS-DYNA 程序中的type24 材料模型。轮胎与定向器选用LS-DYNA 程序中的type1材料模型。货台与轮毂定义为刚体,选用LS-DYNA程序中的type20 材料模型。气囊为纤维编织材料,存在正交各向异性,选用LS-DYNA 程序中的type34材料模型。
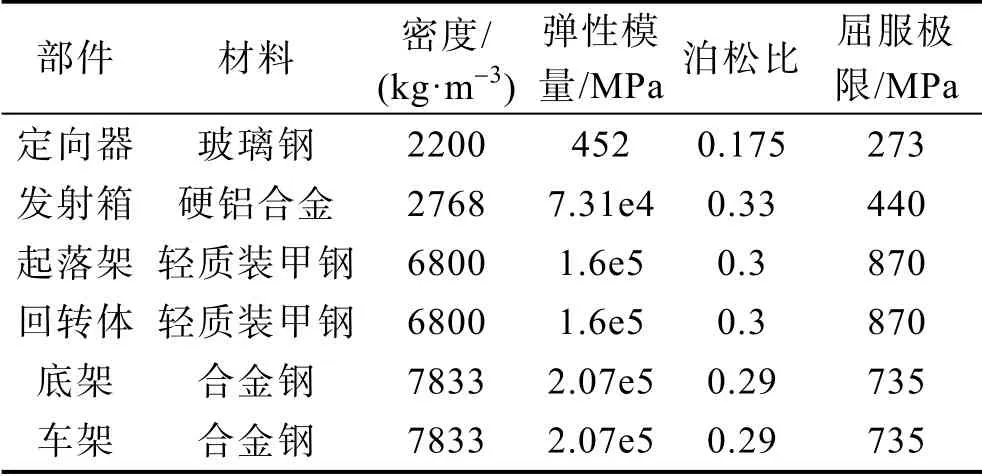
表1 各部件材料参数

表2 气囊材料参数
3.4 边界以及约束条件的施加
火箭炮正常着陆,无横风,软地面,着陆速度为6 m/s,气囊全部有效工作[11]。
整个模型由地面、缓冲气囊和空投装备组成。空投装备包括火箭炮和货台。火箭炮由运载车、底架、座圈、回转体、起落架、发射箱等组成。空投时,火箭炮直接捆绑在货台上,模型中用缆绳单元连接车架和货台,模拟绳索的捆绑作用。车架与底架、底架与座圈、座圈与回转体、起落架与发射箱之间均建立绑定约束关系。起落架可围绕回转体自由俯仰,连接关系采用LS-DYNA 程序中的铰链单元模拟。不考虑地面的动态响应,为简化计算,地面采用LS-DYNA 程序中的刚性墙模拟。在空投过程中,悬架是锁住的,没有缓冲,因此将车架与轮毂的连接设置为刚性连接。气囊的变形属于大变形,气囊壁常常发生自身接触摩擦的情况,因此对于接触的定义,除了要定义气囊与地面、气囊与货台之间的面面接触外,还要定义气囊间的相互接触以及气囊的自接触。
3.5 火箭弹的安全评价准则
用加速度评估火箭弹的安全性,质心位置纵向(以车头指向车尾为正向)加速度不大于98 m/s2,横向(以垂直于地面向上为正向)加速度不大于294 m/s2。用冲击作用下火箭弹的轴向力评估闭锁安全性,向前的轴向力不能超过6000 N[12]。
4 数值仿真模型的计算
已知各部分质量,对火箭炮-气囊系统施加6 m/s的初始速度场,地面四周固定,仿真时间为1.5 s。为缩短计算时间,仿真从气囊底部距离地面0.02 m 处开始。
5 仿真结果与分析
5.1 着陆装备速度分析
提取货台的下落速度变化曲线,如图2 所示。火箭炮-气囊系统的初始速度为6 m/s,在重力的作用下加速下落。在起始的0~0.03 s,气囊对装备的作用力很小,重力为作用于装备的主要作用力。因此,在这段时间内,装备仍向下加速。在0.03 s 后,气囊对装备的作用力成为主作用力。随着装备的下落,气囊被迅速压缩,内压急剧上升。装备在气囊缓冲作用下急剧减速,减速到0 后,有了反向速度,说明装备发生了反弹。反弹的最大速度未超过2 m/s,幅度很小,是可以接受的。0.83 s 左右,速度接近于0,装备成功着陆。
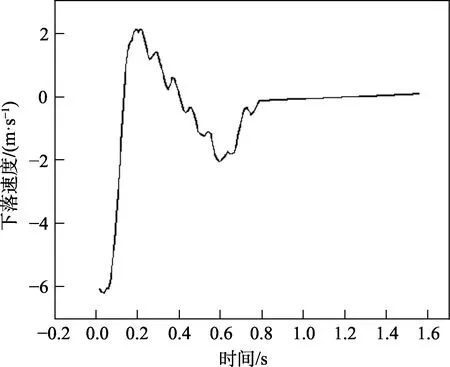
图2 货台速度变化曲线
5.2 缓冲气囊工作状态分析
气囊在着陆缓冲过程中的体积、内压、吸能曲线,如图3—5 所示。由图3 可知,气囊的初始体积为7.8 m3,0.03 s 触地后被压缩,达到一定内压后,气囊开始向外排气释能。由于装备发生反弹,气囊体积在一定时间内维持不变,最后剩余体积0.5 m3。由图4 可知,气囊初始内压为1.013×105Pa,气囊触地开始压缩后,气囊内压急剧增大到峰值1.9×105Pa,随后迅速减小。由于反弹过后,装备下落再次压缩气囊,出现第二次峰值,但囊内压力远小于第一次。由图5 可知,缓冲气囊吸收了大部分的冲击能量,起到良好的缓冲效果。

图3 气囊体积变化曲线
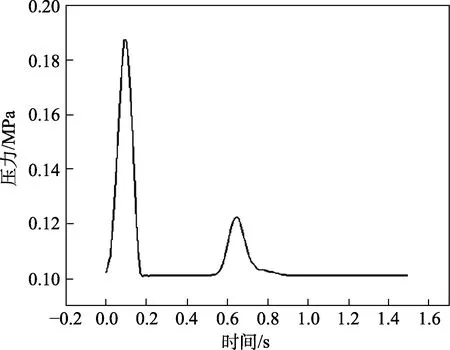
图4 气囊内压变化曲线
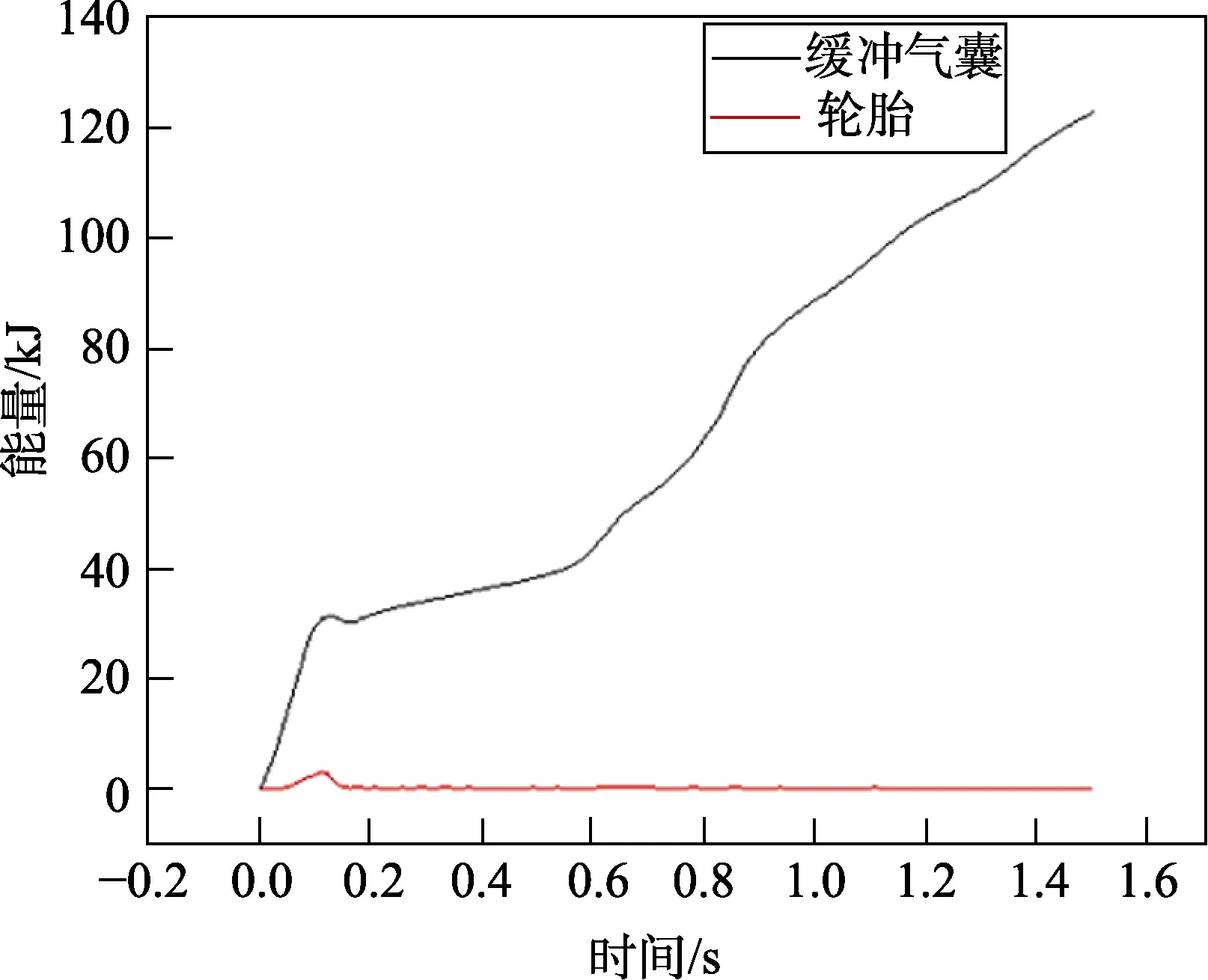
图5 主要部件吸能曲线
5.3 火箭弹冲击分析
分别选取第1、3、16、18 号火箭弹为研究对象(方向为从车尾指向车头),如图6 所示。

图6 火箭弹编号
火箭弹的横向加速度曲线如图7 所示,四个位置火箭弹的加速度比较接近,均不超过140 m/s2,变化规律基本一致。由表3 可知,16、18 号火箭弹的横向加速度大于1、3 号火箭弹的横向加速度,1、16号火箭弹的横向加速度大于3、18 号火箭弹的横向加速度,最大值为122 m/s2。火箭弹纵向加速度曲线如图8 所示,可以看出,火箭弹纵向加速度较小。由表3 可知,1、3 号火箭弹的纵向加速度明显大于16、18 号火箭弹的纵向加速度,但均未超过安全值98 m/s2,最大纵向加速度为48.3 m/s2。

图7 火箭弹横向加速度曲线
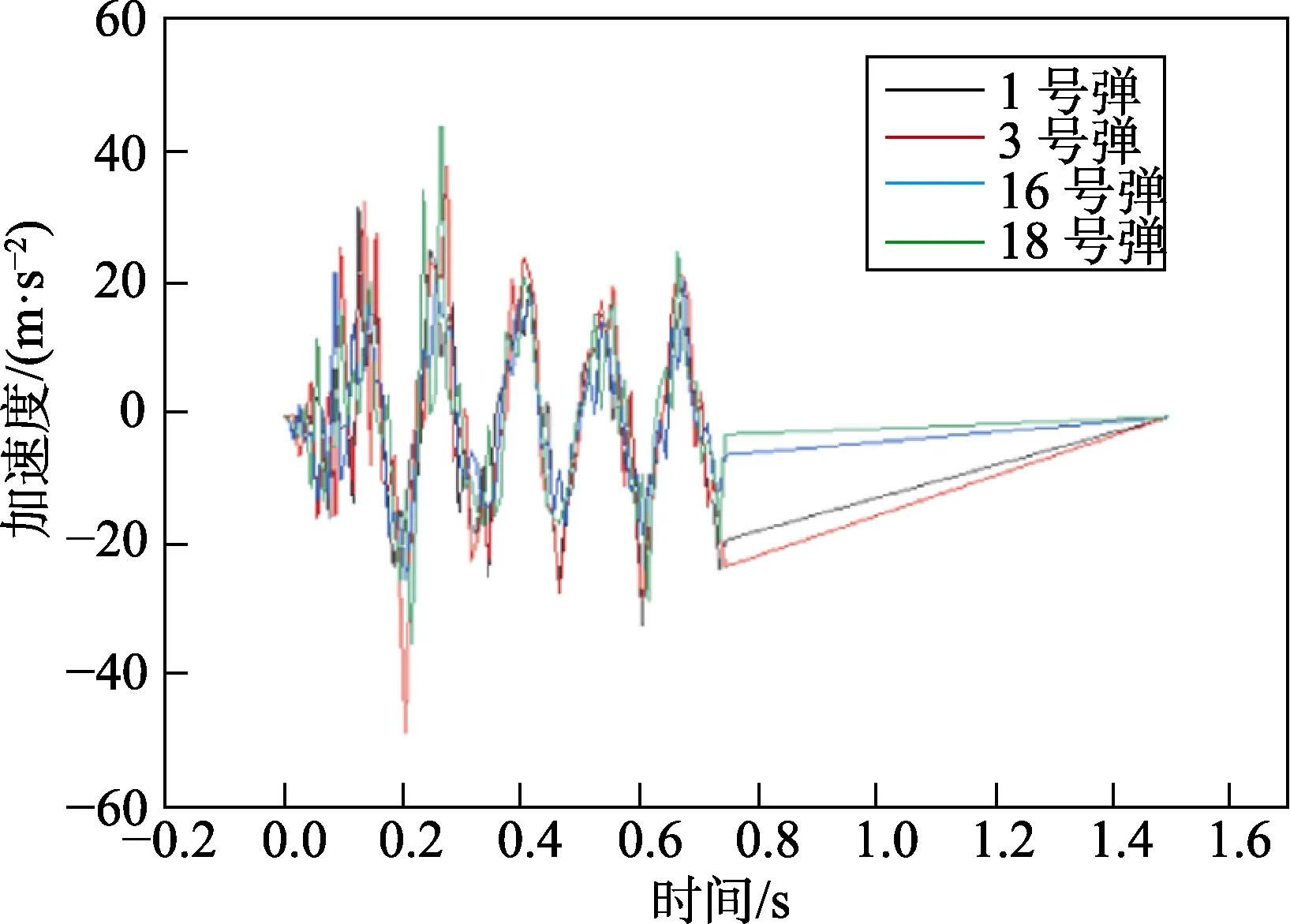
图8 火箭弹纵向加速度曲线
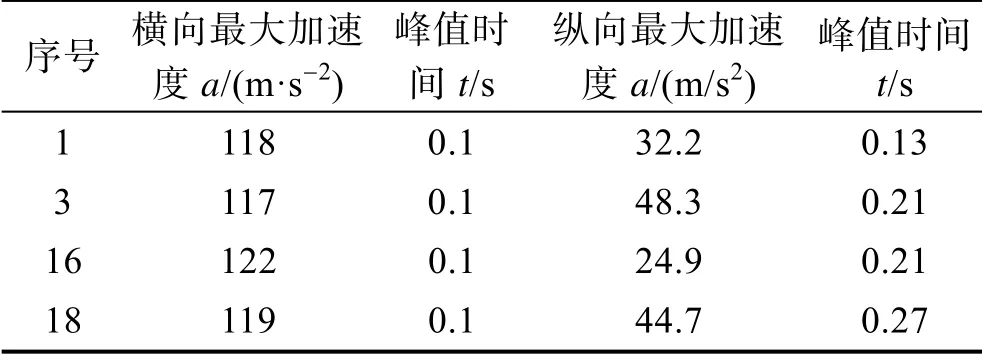
表3 火箭弹加速度峰值
火箭弹纵向惯性力曲线如图9 所示,1、3 号火箭弹的纵向惯性力明显大于16、18 号火箭弹。由表4 可知,纵向惯性力的最大值为2640 N,未超过安全值6000 N,可以判断火箭弹不会从定向器中滑脱。

图9 火箭弹纵向惯性力曲线
6 结语
基于LS-DYNA 软件对火箭炮-气囊系统的着陆缓冲过程进行了研究,得出以下结论。

表4 火箭弹纵向惯性力
1)在正常着陆工况下,火箭弹的加速度与轴向力均小于安全值,火箭弹是安全的。
2)可以考虑对气囊的各参数加以优化(如排气孔开启压力、排气孔面积),最大程度地发挥气囊的缓冲作用,减小着陆冲击。
