高速列车隧道会车流场的CFD 分离涡数值模拟

张德文，卢耀辉，李望，毕伟

（1. 西南交通大学 a. 机械工程学院；b. 先进驱动节能技术教育部工程研究中心，成都 610031；2. 西南交通大学 唐山研究院，河北 唐山 063000）

高速列车隧道会车会引起三维、非定常的湍流流动，产生的气动压力波对高速列车行车安全及乘坐舒适性影响显著[1-3]。我国的武广、郑西等高铁线上隧道占比接近线路总长的20%[4]，列车在隧道内会车频繁，作用于车体的气动载荷可能会对高速列车铝合金焊接车体产生不利影响，故使用数值模拟研究列车会车流场的变化规律可以为高速列车强度、振动及气密设计提供参考。目前，列车空气动力学中的湍流模拟方法、流场压力波消减问题及流、固耦合动力学是研究的热点。梅元贵[5-6]采用流体流动理论结合广义黎曼变量特征线法，对高速列车隧道内会车的压力波进行了研究，通过与国内外试验数据对比，发现设置喇叭型洞口可以缓减压力波。田红旗等[7-8]利用实车试验和数值模拟相结合，研究气动载荷压力波的影响因素，并对车体外形进行优化设计。刘堂红[9]使用滑动网格技术计算了列车通过隧道和两列车在隧道中交会的瞬时压力，分析了气动载荷作用下车身的动态响应。结果表明，在两列车隧道交会时，气动载荷使得底架和侧墙的横向和垂向位移显著增加。赵晶[3]基于k-ε 两方程紊流模型模拟了高速列车的等速交会过程，得到了列车所受气动侧向力、侧翻力矩及偏转力矩的变化情况，结果表明：隧道内列车交会过程使列车受到较大的力及力矩，气动力与力矩的大小是车速的函数。李田[10]建立了基于列车空气动力学和系统动力学的研究方法，实现了流、固耦合的联合仿真。这些研究发现列车受到的气动力对整车振动、车体侧墙强度以及行车安全性均有较为明显的影响，模拟计算多采用雷诺时均法（Reynolds Average Navier-Stokes，RANS），通过对动量方程采取时间平均，忽略了与流动状态相关的瞬态脉动细节，无法计算远离壁面的湍流脉动频谱[11]。雷诺时均法——大涡模拟法（Large Eddy simulation, LES）耦合方法[12]在近壁面区域使用RANS 方法求解，在占主体的外流区域中用大涡模拟法（LES）求解，可以得到优于RANS 的模拟结果[13]。一些学者[14]逐渐开始将其运用到列车空气动力学研究中来，得到了较为理想的结果。

本文采用三维可压缩的分离涡方法（Detached Eddy Simulation, DES）和雷诺时均两种方法模拟高速列车隧道会车流场，分析了列车不同测点的压力变化规律。然后对尾车主要测点的数据进行了频谱分析，最后计算了列车尾流的湍流强度，并讨论了其湍流流动的特性，以期为高速列车振动、强度及气密设计提供参考。

1 列车隧道会车的数值模拟

1.1 控制方程

列车以350 km/h 的速度在隧道内交会，相对速度超过0.3 马赫。流体运动遵循质量守恒定律、动量守恒定律和能量守恒定律，具体表现为连续方程、动量方程和能量方程。如果流动处于湍流状态，还要遵循湍流输运方程。

由质量守恒定律推导出的可压缩流体的连续性方程为：

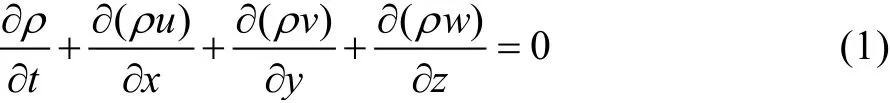
动量方程为：

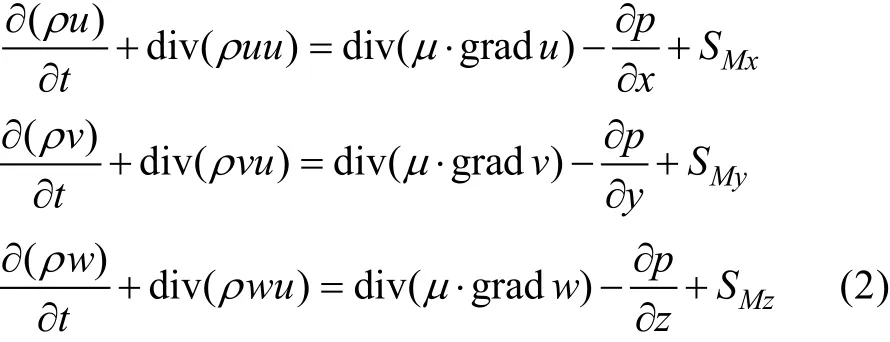
能量守恒方程为：

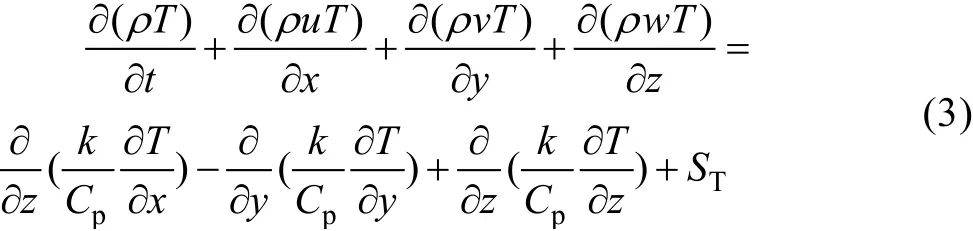
式中：u、v、w 分别为x、y、z 方向的速度分量，SMx、SMy、SMz是广义源项；μ是动力黏度；Cp是比热容；T 为温度；k 为传热系数；ST为内热源或者由于黏性作用流体机械能转换为热能的部分。

流体状态方程为：

SST k -ω 的k 方程为：

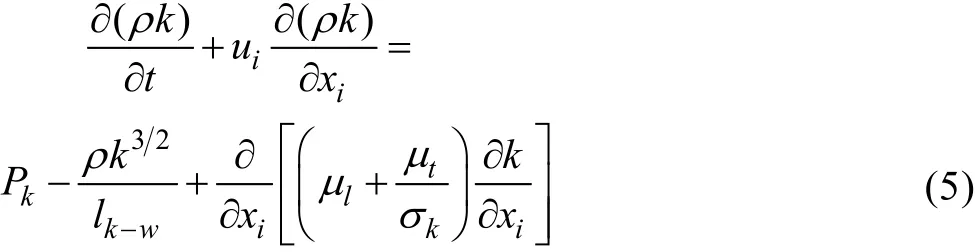
ω 方程为：

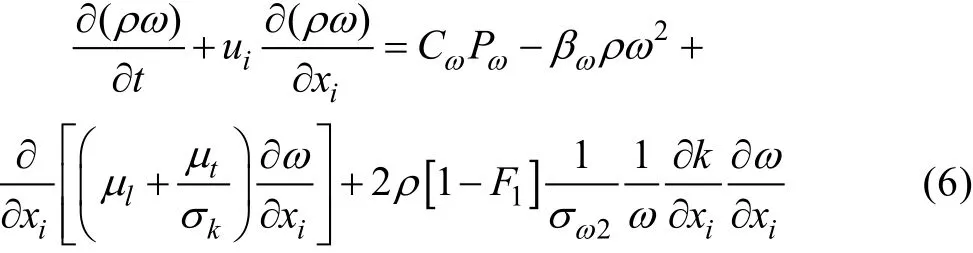
涡粘系数方程由式(7)确定：

式中：kP 和Pω为湍流生成项。脱流尺度参数 lkω-的表达式为：

RANS 和LES 的分辨尺度由式(9)确定：

式中： CDES= 0.65，Δ 是网格尺度。对于非均匀网格有Δ=max（Δx, Δy, Δz）。

1.2 计算模型、计算区域及计算网格

建立三节车的流场模型，其中列车总长76.4 m，最大横截面积11.2 m，隧道横截面上隧道中线间距5 m，隧道横截面积100 m2，阻塞比0.112。简化列车外部复杂突出细节，去掉了门把手、车灯、受电弓及风挡部分，假设列车表面为光滑曲面，列车及部分网格如图1 所示。假设隧道内为平直线路，忽略隧道壁和底面水沟、电缆沟等细节结构。隧道采用的是单孔复线隧道，其长为600 m。初始时刻两列车分别在隧道外30 m处。为了比较准确地模拟列车A与列车B、列车与隧道之间的相对运动，采用滑移网格和动网格结合的方法对其进行模拟。流场边界条件如图2 所示。列车的运动通过用户自定义函数实现（UDF），设置两列车的速度分别为x 方向的97.2 m/s和-97.2 m/s。列车表面设置10 层边界层，第一层厚度为0.4 mm，增长率为1.2。流场最小网格为0.04 m。基本单元包括四面体、六面体、三棱柱。列车运行速度为350 km/h 时，使用车高作为特征长度h 计算的雷诺数Re 超过106，流场处于湍流状态。采用DES模型模拟会车流场，其中的 RANS 模型选择 SST k -ω 模型。采用基于压力的分离式隐式方法SIMPLE 求解。空间离散化压力项、密度项及修正的湍流黏度项使用二阶迎风格式，动量项使用有界中心差分格式。

图1 模型及网格

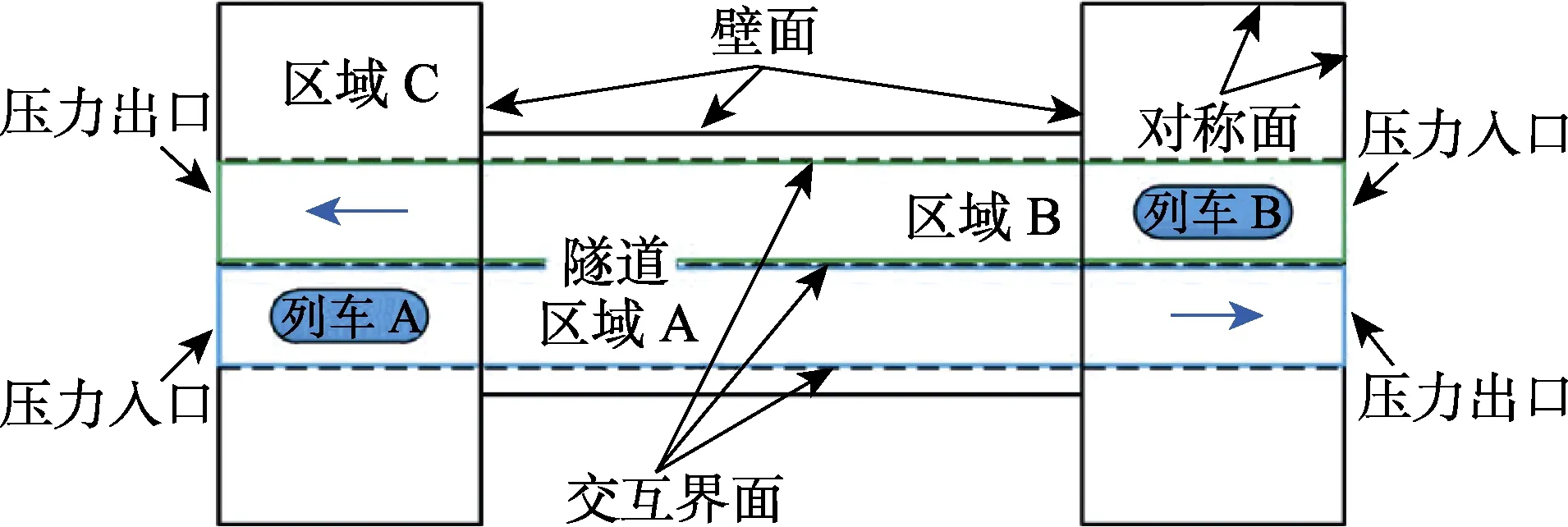
图2 边界条件

1.3 测点布置

为了精确记录列车会车压力波变化情况，在列车会车侧设置19 个测点，如图3 所示。其中测点1、2、17、19 位于列车中轴线，其余测点分布于车头、侧墙。此外，非会车侧设置15 个与会车侧对称分布的测点，中间车车底设置一处测点。

图3 列车表面测点分布

2 结果分析及讨论

高速列车隧道会车的压力波动比较复杂，隧道内压力波传播如图4 所示。当车A 头进入隧道入口时，突然的空间变化会形成压缩波，这种压缩波以声速向前传播，在隧道出口，一部分微气压波向外扩散，一部分以膨胀波的形式向隧道入口传播。当车A 尾进入隧道时，形成的膨胀波以声速传播，在隧道出口以压缩波的形式折返回来。车B 进入隧道同样会形成压缩波、膨胀波。压缩波使得流场压力升高，膨胀波使得流场压力降低，所以高速列车在压缩波与膨胀波来回传播的流场中行驶，流场波动明显。图4 中阴影区域表示两车交会，实线表示压缩波，虚线表示膨胀波。可以看出，在两车交会前，有4 次压缩波扫掠过车A，1 次膨胀波。会车时刻，2 次压缩波扫掠过车A。会车后，车A 遭遇2 次压缩波、2 次膨胀波。使用雷诺时均法与脱体涡模拟法计算所得压力波对比如图5所示，可以发现两者所得压力波数据差别很小。

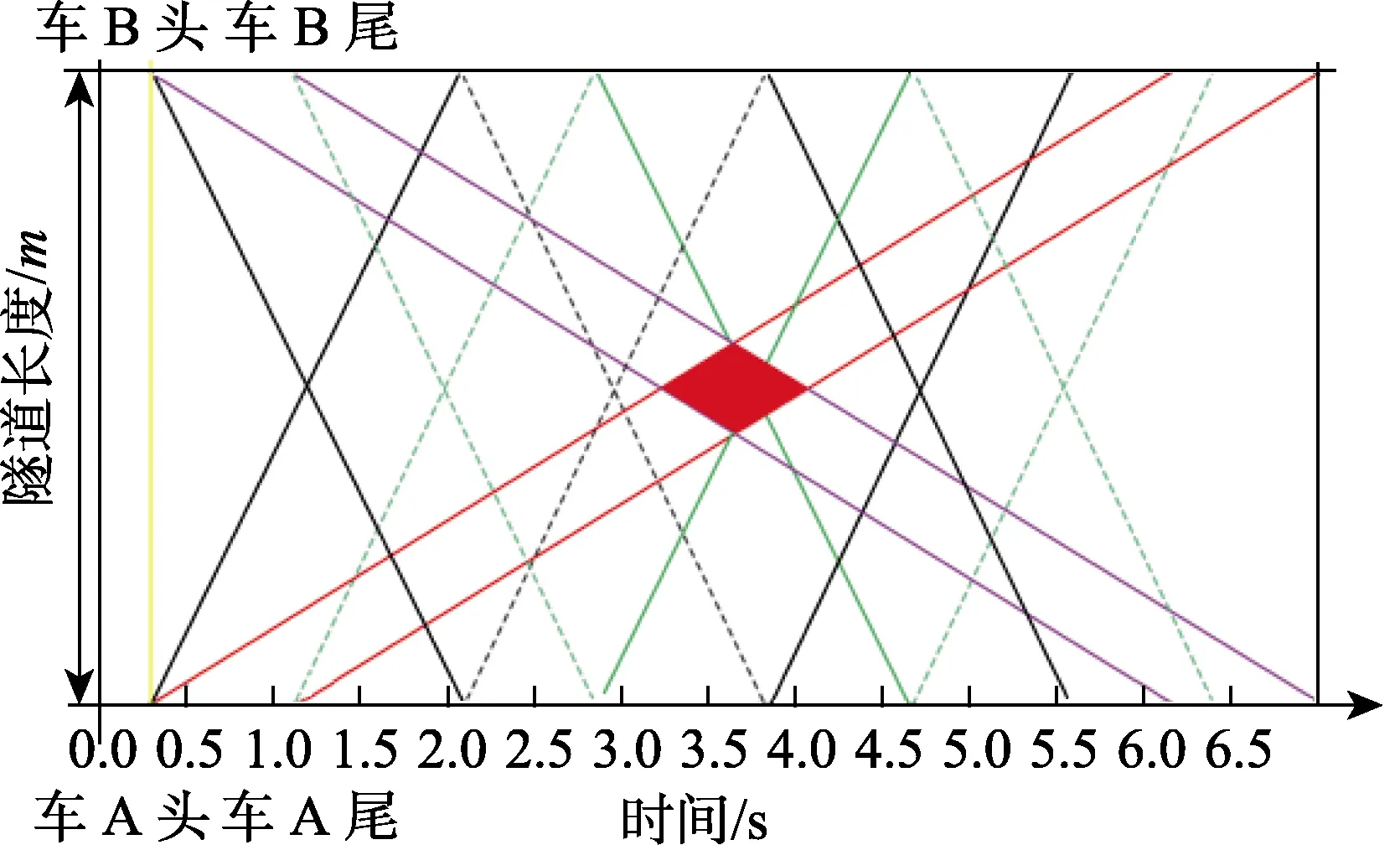
图4 隧道内压力波传播

文中记录了共34 个测点的压力变化，测点4、5、6，测点9、10、11，测点14、15、16 三组均位于同一纵向位置，其压力曲线如图6a、b、c 所示。可以发现，曲线在1.5 s 以后均有一个明显的上扬过程，这是因为车B 的第一轮压缩波扫掠过车A。经过这个压缩波之后，在会车之前，车A 一直经受膨胀波扫掠，整个曲线连续下降至最低点。图6a、b、c 最大负压分别接近5500、4500、4000 Pa，说明车头测点经受了最为强烈的压力波冲击。图6c 在3.5～4.0 s 时程内的曲线与图6a、b 有明显不同，车头通过测点后形成的负压降小于车尾经过测点的负压降，最大负压也产生于车尾通过测点时。这是因为两车尾交会形成一个短暂的负压区域，对车尾测点数据形成比较大的影响，而车头与中间车测点因为距离车尾较远，负压区影响不显著。

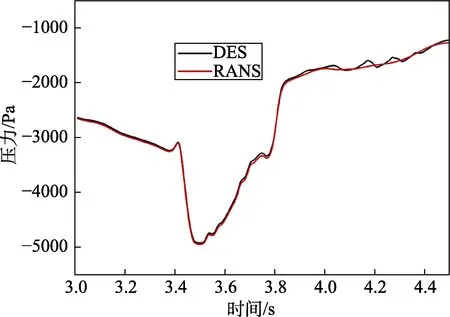
图5 会车时刻压力波对比

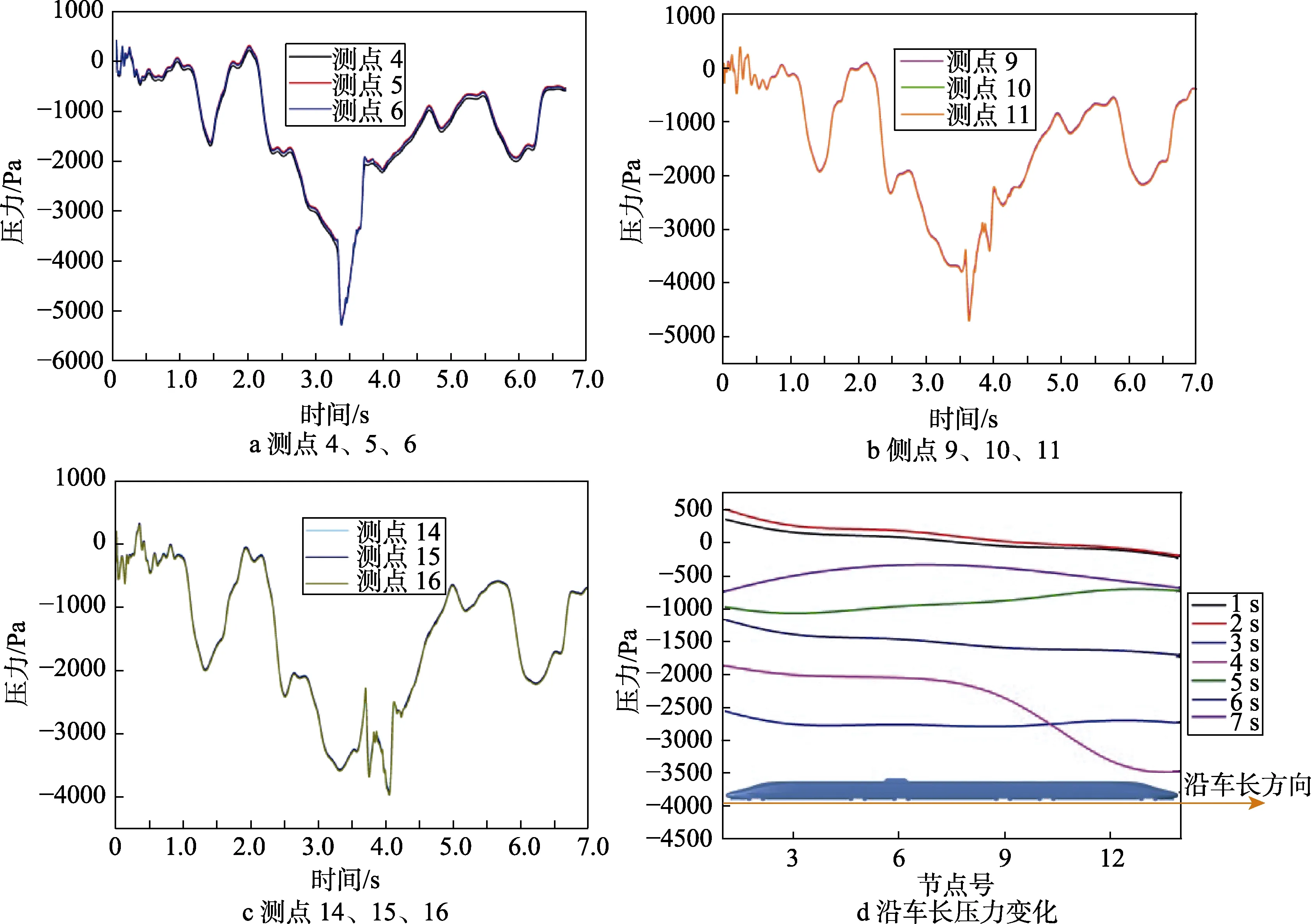
图6 测点压力变化

由图6a、b、c 可以发现，同一纵向尺寸不同高度的测点压力变化几乎一致，并且头车测点压力最大，尾车测点压力最小。测点4、5、6 位于头车变截面车头之后，最大负压超过5500 Pa。中间车测点压力变化曲线（见图6b）在3.5～4.0 s 内显示出车头、车头交会而形成的双波峰、双波谷曲线。图6d 为从头车测点开始沿车身的测点，在不同会车时刻的压力曲线，可以看出，在会车时刻3 s 和4 s，整个会车侧测点承受了最大的负压力，并且4 s 时，整个曲线呈现明显下降的趋势，测点12 的压力值接近3500 Pa。在其余非会车时刻，纵向的测点压力变动不剧烈。

列车交会是一个动态过程，所以列车周围流场随时间不断发生变化。为了比较详细地展示不同时刻列车周围压力的分布，此处提取3.3～4.3 s 的完整会车过程压力云图，如图7 所示。为了清楚显示列车周围压力的变化，每个时刻云图的最大最小基准不同，其中最大负压为7881 Pa，最大正压为6087 Pa。一般来说，车头在向前行驶过程中必须排开静止的空气，使车头前方附近区域为正压区，车头变截面后，车身压力逐渐减弱为负压，车尾区域处于较大负压区。因此当车头通过对向列车的测点时，会使测点压力瞬时升高，车尾通过测点会使测点压力瞬时降低。3.7 s 时刻，两列车尾车之后的涡旋最为剧烈，可以清楚地看出涡旋在车后延伸。

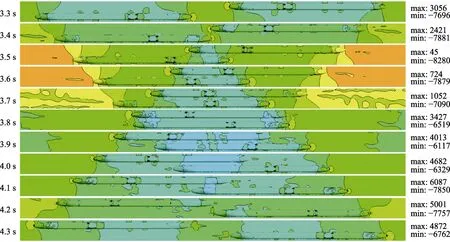
图7 列车交会压力分布随时间的变化

高速列车周围流场随时间波动，并且车尾会形成螺旋状的涡旋不断破裂，向列车后方扩散，形成具有一定规律的涡流结构。由于列车并不位于隧道中心，故尾涡并不对称，靠近隧道中心的涡旋会逐渐向隧道另一侧移动，涡旋逐渐增大，但强度衰减，最终消散。对于涡旋的识别方式，常用的有涡旋强度和Q 判据。涡旋强度为速度梯度张量（见式（10））复特征值的虚部，当判别式为正且其值代表局部中心周围的旋转运动强度时，它是正的[15-16]。

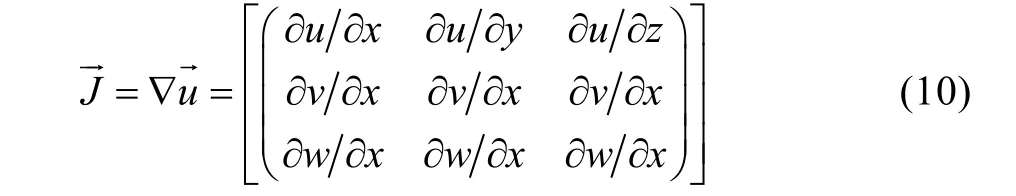
负值旋转强度代表局部旋涡运动，局部最小值代表涡旋核心。当负值旋转强度的绝对值越大，内部循环越强。

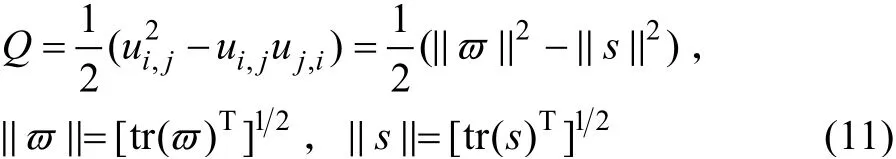
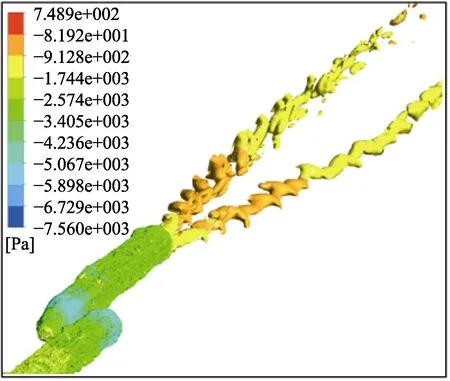
图8 Q 准则尾涡示意（t=3.65 s）

为了评价尾车尾流特性，定义湍流强度为：

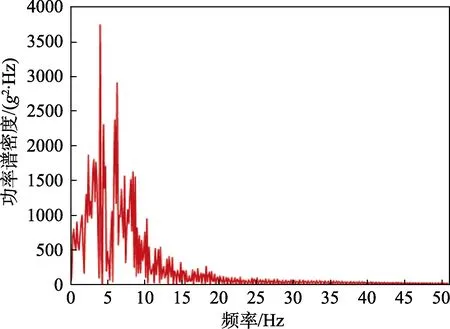
图9 测点压力功率谱密度

以车高为特征长度h，对变量进行无量纲化。选择列车会车时刻3.65 s 为研究时刻，则根据模型在计算域中的位置，车底面z=0；隧道中点x=0 且y=0。确定垂向z=0.05h、0.15h、0.25h 时，平面上不同横向位置（y=0.5h、0.75h、0.85h）处湍流强度沿直线的变化曲线如图10。

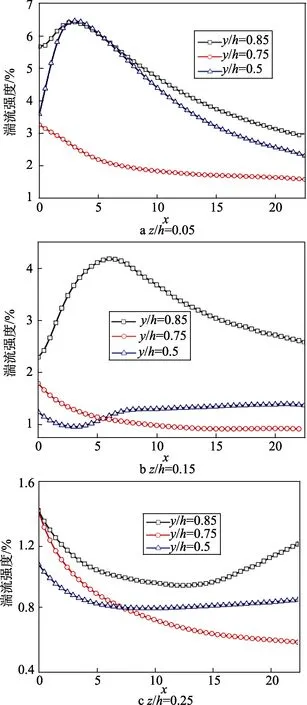
图10 不同位置处湍流强度沿流向变化曲线

由图10 可见，z 为0.05h 时，湍流强度最大，最大值接近0.065。随着垂向平面的抬升，湍流强度减弱，z 为0.25h 时，湍流强度小于0.016。从沿流向的变化规律看，当z=0.05h、0.15h 时，湍流强度在在y=5h附近会有一个明显的增强，之后持续减弱，这可能与涡流横向移动、会车压缩波及膨胀波复杂作用有关。从横向分布来看，y 为0.85h 的一侧靠近隧道壁面，其湍流强度较大。在会车一侧的涡流横向发展较快，导致其湍流强度较小，减弱速度较快。总的来看，湍流强度在流向是成减弱趋势，涡流携带的能量不断减小，在20h 以后逐渐减弱为低湍流强度流动。

3 结语

采用脱体涡方法数值模拟研究了两列高速列车在隧道内交会的流场，分析了随时间的变化，列车不同位置的压力分布，并对其进行了频谱分析。计算了尾涡流向不同位置处的湍流强度变化规律，得出以下主要结论。

1）使用脱体涡方法模拟会车流场可以较好地模拟列车流场，在计算精度和计算经济性比较均衡的情况下能够清晰地捕捉会车时产生的涡旋。

2）高速列车会车时车头受到的负压最大，最大值接近8 kPa，在车体强度设计时应该考虑压力波对强度的影响。

3）经过频谱分析发现，尾车产生的涡旋主频为3.85 Hz，属于车体的低频振动范围，对高速列车的横向振动和行车安全有影响，为高速列车车体动态设计提供参考。

4）高速列车隧道会车时产生的尾涡是两个不断向后发展的中等强度涡旋，在充分发展阶段，其湍流强度会有一个较为明显的抬升，之后逐渐减弱。会车侧涡流由于横向发展较为迅速，导致其强度较小且减弱速度较快。