一种三轴振动载荷谱保型裁剪方法

白 金，仇原鹰,李 静，王钊倩，李贵林，

王海东2，王肇喜2

(1. 西安电子科技大学机电工程学院,陕西西安710071；2. 上海航天精密机械研究所,上海201600)

结构在服役过程中的振动环境一般都是多轴随机振动，因此，在环境试验中通过随机振动试验考核结构的功能是否完好[1]。早期由于多轴振动试验台控制技术并不完善，无法实现多轴向同时振动，所以研究者提出以三个正交轴依次进行的单轴振动试验的方式代替多轴向同时振动[2]。虽然在初期的工程实践中该方法的适用性得到了一定程度的认可，但随着研究的深入，此类方法的有效性受到了质疑。文献[3]研究指出，单轴振动试验并不能筛选出产品的所有缺陷。同时，不少学者通过对比某些产品在单轴与多轴振动下响应的差异，发现结构在多轴振动激励下响应耦合效应十分复杂[4]。FRENCH等[5-9]的研究表明，相比于单轴振动，三轴同时振动会导致结构产生更大的疲劳损伤。

由此可见，不能简单地以三个正交轴依次进行的单轴振动试验来等效多轴振动试验，但目前关于三轴振动的试验标准尚不成熟，在GJB150A[10]和MIL-STD-810G[11]中也没有相应标准的确切描述，而简单地将单轴依次振动对应的三个方向的载荷谱同时作为三轴振动载荷谱进行三轴振动试验则会对产品造成过试验。因此，如何得到合理的三轴振动试验标准引起了相关学者的注意。

有学者开始研究如何根据单轴振动试验标准建立与之等效的三轴振动试验标准。王海东等[12]基于单轴载荷谱提出了一种三轴载荷谱裁剪方法，为三轴振动试验研究提供了一个有益的思路。但该方法有以下两个问题：其一是按照“最大应力等效”的裁剪方法在对某电子舱段进行载荷谱裁剪后，在三轴振动试验时，舱段内部电路板出现了引脚焊点失效。原因是由于三轴载荷下等效应力点虽然仍保持在单轴载荷时最大应力出现的同一紧固螺栓上，但其应力远未达到该高强度螺栓材料的许用应力，而此时电路板引脚的焊点处应力却已经超出了其单轴振动时的最大应力，且超过了材料的许用应力，从而对该电路板造成过试验；其二是未明确给出载荷谱谱型的裁剪原则，因不同的谱型有可能围成相同的面积，这导致裁剪的不确定性。

通过考虑结构中不同部位对结构性能影响程度的不同，分别从以避免重要零部件过试验为前提，或者以筛选出重要零部件的更多潜在缺陷为前提，定义不同的载荷谱均方根值裁剪准则，同时通过考虑避免因谱型裁剪的不确定性造成载荷谱等效不当，提出了三轴振动载荷谱的保型裁剪原则，进而裁剪三轴载荷谱，使得关键点处三轴振动时的等效应力与单轴振动时最大振动等效应力相等，进行基于应力等效的三轴振动试验谱研究。

1 基于线性系统载荷与响应关系的载荷谱均方根值裁剪

1.1 线性系统三轴向随机载荷与响应的传递关系

由于讨论三轴与单轴振动的等效问题，故从频域角度推导线性系统在三轴平稳随机载荷下，载荷与响应之间的传递关系。系统频域传递模型如图1所示。其中，X1(ω)、X2(ω)、X3(ω)为作用于系统沿三轴向的输入平稳随机载荷。根据随机振动中自功率谱的定义可知，当三个轴向的X1(ω)、X2(ω)、X3(ω)随机过程同时激励时，任意轴向载荷的均方根值[13]为

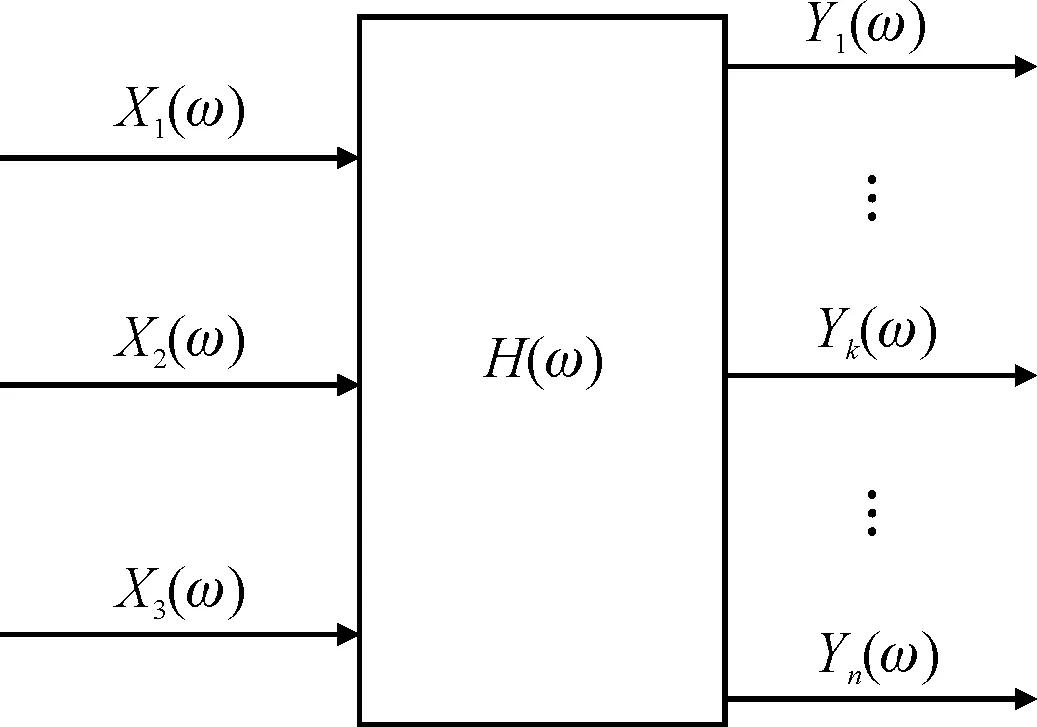
图1 三输入多输出系统激励与响应

(1)

且三轴载荷互不相关时，即输入功率谱互谱为零，则系统中任意一个响应Yk(ω)(k=1,2,…,n)的响应自谱为[13]

(2)

在频域内对上式做关于ω的积分并开方，得到第k个响应的均方根值[13]为

(3)

若将每个载荷的均方根值增加至原来的C倍， 则每个载荷的自功率谱密度函数将增加至原来的C2倍，此时该系统第k个响应的均方根值为

(4)

从式(4)不难看出，对于线性系统，当输入的载荷功率谱均方根值增大至原来的C倍时，系统响应均方根值也增加至原来的C倍。

1.2 基于应力等效的载荷谱均方根值裁剪方法

根据1.1节中的结论，提出载荷谱均方根值裁剪方法如下：计算三轴振动载荷谱裁剪前关键点的von-Mises等效应力与三个轴分别振动时关键点的最大von-Mises等效应力的比值，以该比值为均方根值裁剪系数，得到相应三轴振动载荷谱的均方根值。根据式(4)有

(5)

其中,G′rms、Grms分别为剪裁前后载荷谱的均方根值；σΙ为关键点在单轴单独加载时最大振动方向下的von-Mises等效应力；σΙΙΙ为关键点处三轴振动裁剪前的von-Mises等效应力。

2 基于关键部位应力等效的载荷谱保型裁剪方法

2.1 基于结构关键点应力等效的载荷谱均方根值裁剪准则

若只是单纯地考虑最大应力等效，则可能会给试验判定带来一些误区。因此，关键点的选取在载荷谱的裁剪过程中至关重要，关键点选取不同就会得到不同的载荷谱均方根值裁剪系数。故提出以下四条基于结构关键点的均方根值裁剪准则：

准则1若整个结构零部件的重要程度相同，则选取三轴同时加载时结构的最大等效应力点为关键点，定义裁剪系数为

(6)

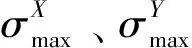
准则2若整个结构零部件的重要程度不同，且所有最重要的零部件都是同一类部件，则选取三轴同时加载时结构最重要零部件的最大等效应力点为关键点，定义裁剪系数为

(7)

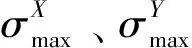
准则3若整个结构零部件的重要程度不同，且所有最重要的零部件不是同一类部件，同时试验原则为避免最重要零部件过试验，则应首先分别计算各类最重要部件三轴同时加载时最大等效应力点处在X、Y、Z轴单独加载时最大等效应力与三轴同时加载最大等效应力的比值，然后对比各类部件比值的大小(即裁剪系数)。选取比值最小点为关键点，定义裁剪系数为

(8)

准则4若整个结构零部件的重要程度不同，且所有最重要的零部件不是同一类部件，同时试验原则为筛选出最重要零部件的更多潜在缺陷，则应首先分别计算各类最重要部件三轴同时加载时最大等效应力点处在X、Y、Z轴单独加载时最大等效应力与三轴同时加载最大等效应力的比值，然后对比各类部件比值的大小(即裁剪系数)。选取比值最大点为关键点，定义裁减系数为

(9)

2.2 基于关键点应力等效的载荷谱保型裁剪规则

载荷谱谱型的裁剪前提是避免过试验或者欠试验的同时，保证试验效果等效。受反射面天线保型优化设计[14-16]思想的启发，提出下述载荷谱保型裁剪规则：

(1)三轴振动载荷谱的扫频范围应保持与单轴振动试验谱的扫频范围相同。

(2)载荷谱斜线段的斜率体现双对数坐标下功率谱密度的变化率，保持斜率不变，即保持载荷能量的增量相同。

(3)三轴振动载荷谱平直谱覆盖的频段应保持与单轴振动试验谱平直谱覆盖的频段一致，以在同样的带宽范围内保持载荷能量的恒定。

根据以上规则，裁剪得到的三轴载荷谱与单轴载荷谱在形状上“保型”，在载荷效果上合理等效，同时根据文献[17]中介绍的加速度功率谱均方根值的计算方法可知，任意裁剪系数均可按照以上裁剪规则得到惟一确定的三轴载荷谱。

3 仿真算例

单轴振动试验，即沿X、Y、Z方向分别加载单轴振动载荷谱；而三轴振动试验，即沿X、Y、Z方向同时加载三轴振动载荷谱。选择国军标规定的宽带加速度随机载荷谱对结构进行随机激励[10]，参见图2。图2中为双对数坐标，斜率用分贝/倍频程(dB/OCT)来表示。根据文献[17]可知，该载荷谱均方根约为6.056(g)。以该载荷谱对算例进行两种工况研究。

算例如图3所示。舱段两端面通过夹具的上下卡环紧密贴合，夹具底部通过高强度螺栓与振动台紧固连接。舱段主要由电气控制板、惯导板、电源板、引信板、计算机板和舱段外壳等结构组成。仿真分析中所有接触部件均设定为绑定接触。网格划分采用人工控制和自动划分相结合的方式。网格单元数为289 277，节点数为923 644，平均网格质量约为0.703。

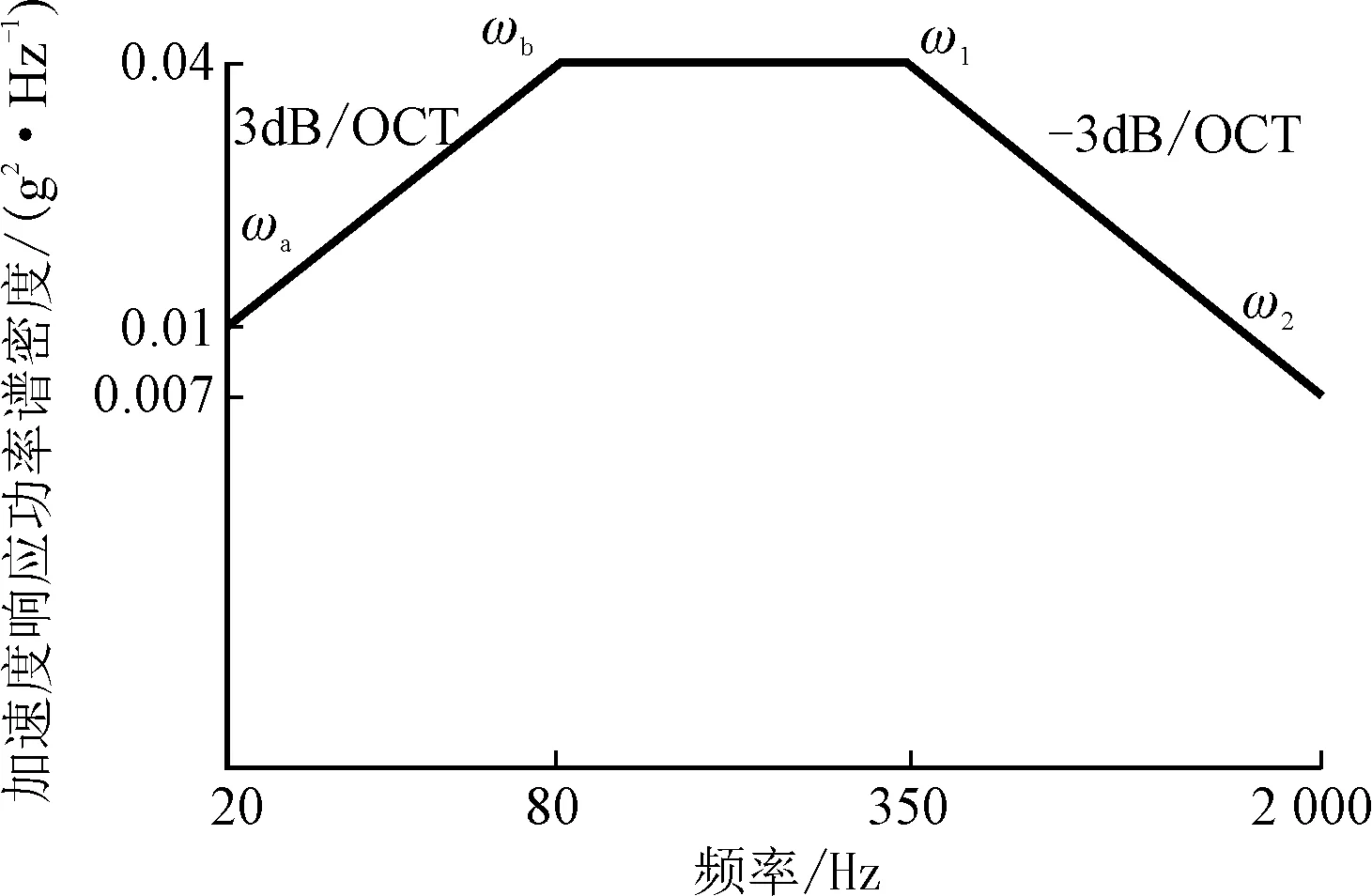
图2 输入加速度功率谱曲线图

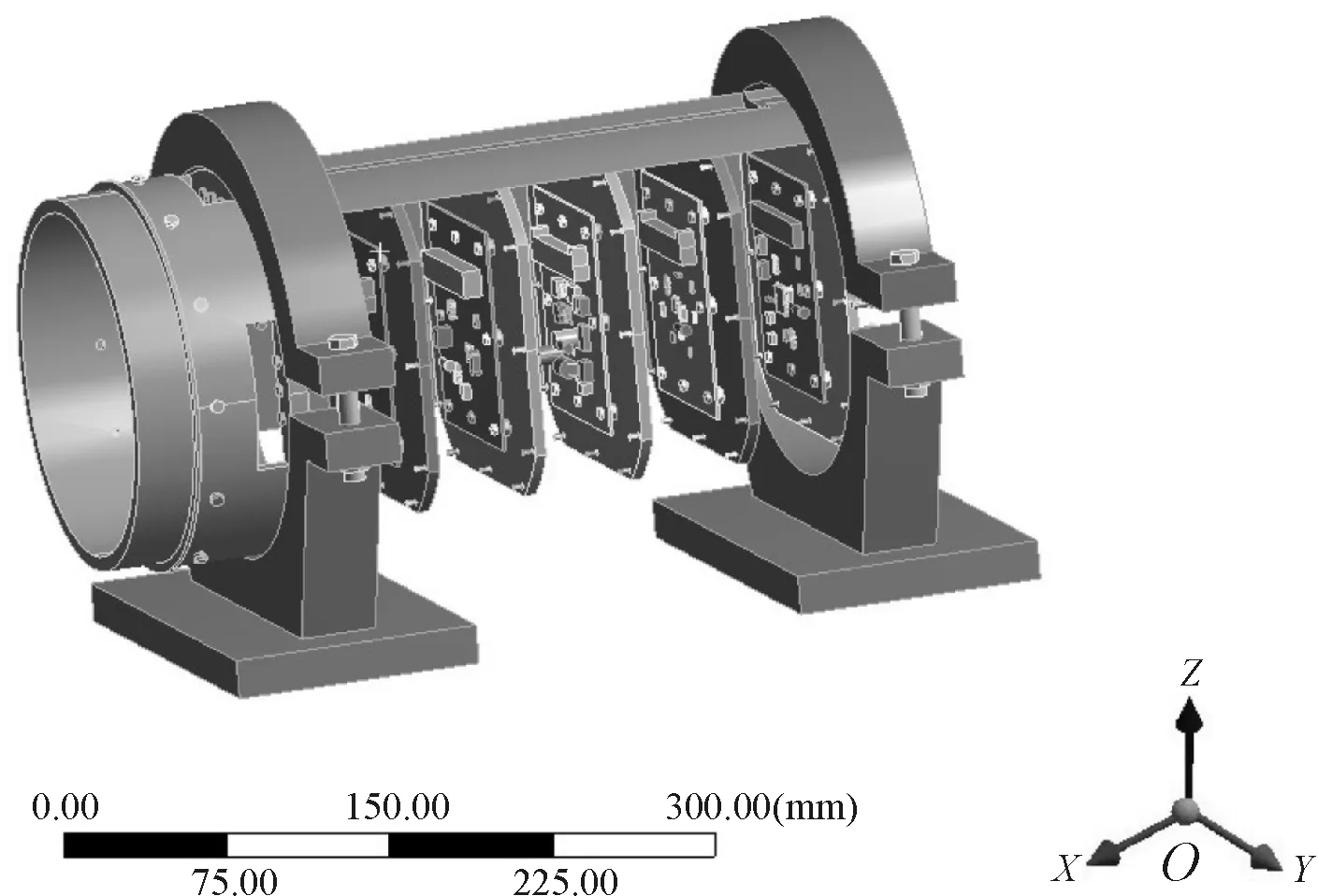
图3 舱段与夹具模型剖视图

图4 舱段结构有限元网格划分图

经过有限元仿真分析得到三轴同时加载时的von-Mises等效应力，如图4中(a)、(b)所示，舱段结构最大等效应力发生在螺钉上的C点、电容处最大等效应力位置处D点，插针最大等效应力位置处E点、引脚最大等效应力位置F点。将C、D、E、F视为备选关键点，并将各点处单轴单独加载与三轴同时加载时的von-Mises等效应力计算结果列于表1。

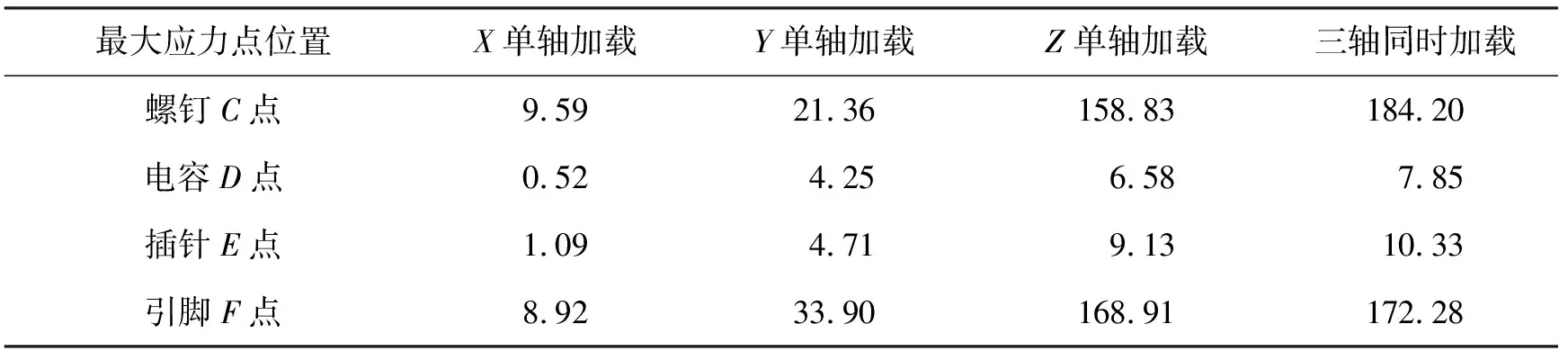
表1 备选关键点处不同工况下的von-Mises等效应力 MPa

若整个舱段结构零部件重要程度均相同，根据准则1，则将三轴同时加载时结构的最大等效应力点选为关键点，即确定螺钉C点为关键点；若整个舱段结构零部件重要程度不同，且电容为最重要部件，根据准则2，则选取三轴同时加载时结构最重要零部件的最大等效应力点为关键点，即电容D点为关键点。结合式(6)、式(7)和表1，计算C点对应的裁剪系数约为0.862 3，D点对应的裁剪系数约为0.838 5，结合载荷谱保型裁剪规则可得裁剪后的载荷谱。

若整个舱段上插针和引脚同为最重要部件，同时试验原则为避免最重要零部件过试验，则先分别计算插针E点、引脚F点在Z轴单独加载时的等效应力与在三轴同时加载时的等效应力的比值，结合式(8)、式(9)和表1，E点应力的比值约为0.883 8、F点应力的比值约为0.980 9，同时若试验原则为避免最重要零部件过试验，根据准则3,则应选择插针上的E点为关键点，即取裁剪系数约为0.883 8；若试验原则为筛选出最重要零部件的更多潜在缺陷，根据准则4,则应选择引脚上的F点为关键点，裁剪系数约为0.980 9，结合载荷谱保型裁剪规则可得裁剪后的载荷谱。

裁剪前后的载荷谱如图5所示。

图5 裁剪前后载荷谱对比图

在仿真软件中，分别将不同裁剪系数对应的裁剪载荷谱同时加载到三个轴向，进行三轴振动仿真分析。其中F点裁剪前后的1σ应力云图如图6(a)、(b)所示，对比表1中的数据，可知F点处的等效应力在裁剪前的Z向单轴随机振动与裁剪后的三轴随机振动下，保持了小数点后两位相同，即达到了对结构关键点实现应力等效的目的；图6(c)、(d)为裁剪前后F点处加速度响应功率谱密度函数图，显然裁剪前后对应的峰值的大小有所减小，且裁剪前后X、Y、Z三向加速度响应均方根值之比均与F点对应的裁剪系数0.883 8非常接近，误差来自于曲线的积分误差。

同理，对其余关键点进行裁剪后可以得出，无论以哪一种关键点选取准则进行裁剪，均可以达到对结构关键点实现应力等效的目的。且以准则3裁剪时，所有与最重要部件不会出现过试验；以准则4裁剪时，所有最重要部件不会欠试验。

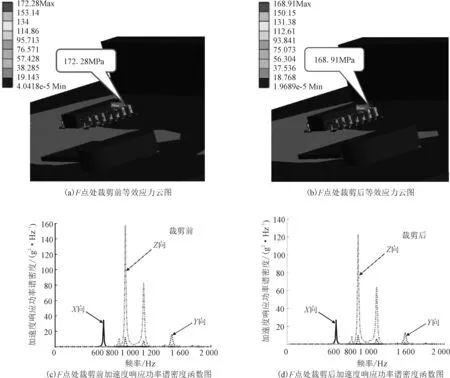
图6 F点处裁剪前后等效应力云图及加速度响应功率谱密度函数图

4 结 论

推导了三轴向随机载荷与结构关键点响应的传递关系，提出了一种基于结构关键部位三轴与单轴随机振动应力等效的载荷谱裁剪方法。

为了避免对关键零部件造成过试验或欠试验，制定了四条不同的关键点确定方法：①当整个结构零部件的重要程度相同时，直接将三轴同时加载时结构最大等效应力点处视为关键点；②当结构零部件重要程度不同，但最重要零部件都是同一类部件时，直接将三轴同时加载时结构最重要零部件最大等效应力点处视为关键点；③当结构最重要零部件不是同一类部件时，若以避免最重要零部件过试验为原则，则载荷谱裁剪幅度取最大的一个；④当结构最重要零部件不是同一类部件时，若以筛选出最重要零部件的更多潜在缺陷为原则，则载荷谱裁剪幅度取最小的一个。

为了避免因不同谱型裁剪方式造成试验结果的不确定性，提出了三轴载荷谱的保型裁剪规则：保持原有单轴载荷谱的形状，只裁剪载荷谱的高度。

针对某典型舱段结构的三轴载荷谱裁剪案例，验证了应力等效裁剪方法的有效性。