一种叶片裂纹检测的稀疏共振解调算法

贺王鹏，胡 洁，陈彬强，李 诚，郭宝龙

(1.西安电子科技大学 空间科学与技术学院，陕西 西安 710071;2.厦门大学 航空航天学院，福建 厦门 361005)

叶轮机械是航空航天、电力生产及舰船等工业系统中广泛使用的重要功能部件[1]。随着我国高端装备制造业的迅猛发展，对叶轮机械在转速、效率、精度及可靠性等方面的性能提出了更加严苛的要求。然而，恶劣的工作条件往往诱发叶轮机械产生多种形式的疲劳失效，甚至造成重大经济损失并诱发人员安全事故[2]。为确保叶轮机械在其服役期限内安全可靠地运行，及时排除叶片故障造成的潜在安全隐患，先进的振动状态监测及故障诊断手段不可或缺[3]。

针对运行状态中叶片振动测量的问题，传统的应变片测量技术虽已成熟，但在工程实际测量中难以全面推广[4]。叶尖定时作为一种非接触式测量方法，通过叶片振动参数的变化来检测叶片的疲劳失效，然而该方法传感设备的部署对现场条件依然有较高的要求。振动量(位移、速度、加速度信号) 测量是简便且可靠的振动测试方法，其传感器常安装在轴承座及设备的金属表面。它所记录的信号中除与故障相关的关键信息外，往往包含多个干扰成分[5]。因而，如何在强噪声背景下有效地提取叶片故障的微弱特征已成为学术研究的热点问题。小波变换是经典的多尺度分析方法，可以对时域上耦合的成分进行分离，但小波基函数的构造不是任意的，其特征自适应能力匹配受到一定的限制[6-7]。为提高故障特征的自适应匹配能力，稀疏表示近年来不断发展，可以融合多种信号模型对故障信息进行深入挖掘[8-9]。

针对叶轮机发生裂纹时出现的周期性冲击故障特征提取问题，笔者提出了一种稀疏表示增强的共振解调方法。该方法采用中心极化多分辨分析(Centralized Multiresolution Analysis, CMA)对振动信号进行多尺度分解。中心极化多分辨分析通过单一基函数及改进的滤波器组结构对信号围绕固定中心频率实现多分辨分析。为抑制多尺度分析子空间内的强相干噪声，采用频域上的梳形滤波器对子空间信号的希尔伯特包络解调谱进行处理，保留故障频率及其倍频成分。最后通过小波降噪方法进一步提取周期性冲击故障特征。在某发电机组的离心式叶轮压缩机上采集了振动位移信号，采用笔者提出的方法对该案例的动态信号进行处理，有效地从低信噪比的时域波形中增强了与叶片裂纹故障相关的特征成分，从而验证了所提出稀疏共振解调的有效性及实用性。

1 中心极化多分辨分析理论

1.1 经典小波包分析的缺陷

经典的小波包变换采用单一尺度函数φ(t)及单一小波函数ψ(t)对输入信号进行基于内积匹配的迭代分解：

(1)

式中，变量s代表伸缩，变量τ代表平移。当信号的采样频率为fs时，子空间{wp(n)}的中心分析频率(Central Analysis Frequency, CAF)为

(2)

其中，j表示小波包分解层数，k表示按频带能量重心从小到大排列的小波子空间的序号。由此可知，每个小波包拥有独一无二的中心分析频率。因此对子空间过渡带特征，小波包变换的特征提取能力受到一定的限制。

1.2 隐小波包尺度的构造

为了提高小波变换对子空间过渡带特征的提取能力，通过子空间{wp(n)}的后处理构造了隐小波包(Implicit Wavelete Packet, IWP)尺度。深度为j的小波包变换间接产生2j-1-1个隐小波包，其时域信号表示为

xj,k(n)=wpj,2k(n)+wpj,2k+1(n) ，

(3)

其中心分析频率可以表示为

(4)

因此，在多个尺度上可以出现具有相同中心分析频率的隐小波包，形成了围绕固定中心频率的多分辨分析能力。经典小波包尺度与隐小波包尺度的关系如图1(a)所示。

1.3 中心极化多分辨分析的频率-尺度划分网格

在对信号的分析中，可以结合不同分析深度的小波包分解并构造对应的隐小波包尺度。基于双树复小波基(Dual Tree Complex Wavelet Basis, DTCWB)，笔者构建了中心极化多分辨分析。在一个DTCWB中，小波函数的虚部ψIm(t)与实部ψRe(t)构成一个希尔伯特变换对[10]，表示为

ψIm(t)=H{ψRe(t)} ，

(5)

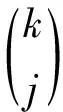
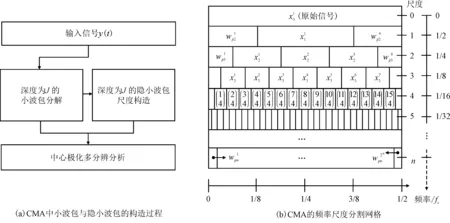
图1 中心极化多分辨分析中小波包与隐小波包的构造过程及频率-尺度分割网格

2 稀疏共振解调方法

某些干扰成分的频谱可能与小波子空间的理论通带高度重合，这类噪声称之为强相干噪声。针对强相干噪声的抑制问题，笔者提出了稀疏共振解调方法。首先介绍算法的两个重要组成要素，即梳形滤波器及硬阈值降噪方法，再给出完整的算法流程。

2.1 梳形滤波器

带通滤波器通常具有单一的通带，用参数组合{CF,RB}表示，其中CF表示中心分析频率，RB表示带通半径，如图2(a)所示。为了增强子空间的周期性冲击成分，需要对特征频率及其倍频进行选择性保留。笔者提出的梳形滤波器如图2(b)所示。它的理论带通可以表示为

(6)

其中,fc表示故障特征频率，M表示等间隔窄带滤波器的总数。

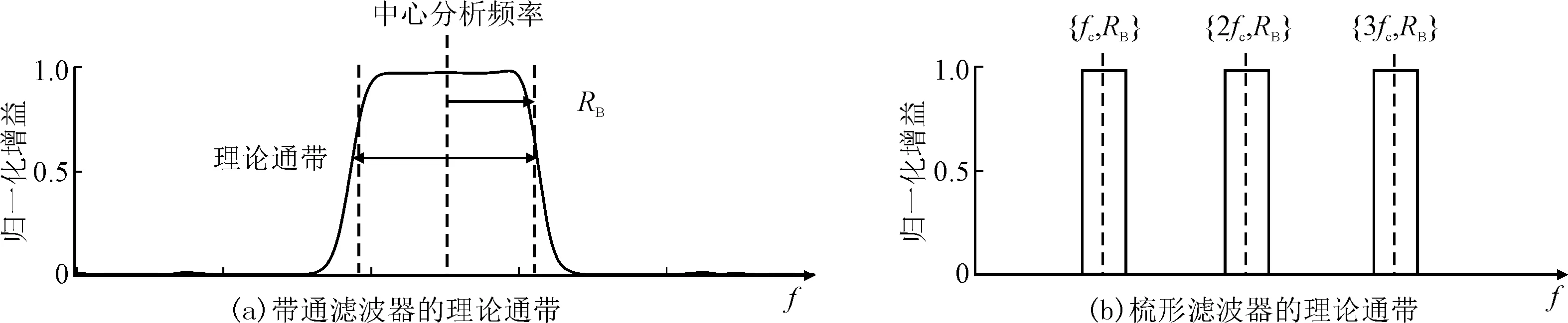
图2 两种滤波器的理论通带

2.2 小波系数硬阈值收缩

信号中的噪声成分通常体现为幅值较小的小波系数。目前学术界已经提出多种不同的小波阈值收缩算法，其算法原理都是将幅值较大的系数保持不变而将幅值较小的系数收缩为零，从而实现噪声抑制的目的。对于小波子空间序列{wpj,k(n)}，硬阈值收缩的数学表达式可以表示为

(7)

收缩阈值的临界值Tj选为

(8)

其中m{·}表示取序列中值的函数。

2.3 算法流程

输入的数据表示为wpj,k(n)，设原始采集得到信号的采样频率及数据长度分别为fs和N，叶轮机系统的故障频率为fc，稀疏共振解调算法的流程为：

步骤1 对输入的振动信号进行中心极化多分辨分析的多尺度分解。

步骤2 对wpj,k(n)进行希尔伯特包络解调，得到瞬时幅值曲线Ej,k(n)。

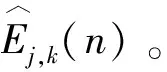
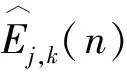
(9)

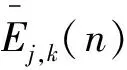
3 叶轮机裂纹检测工程应用

我国某钢铁制造商回收高炉煤气(Blast Furnace Gas，BFG)进行发电，以减小直接排放回收高炉煤气造成的环境污染。该回收高炉煤气燃烧机组的增压风机在一次运行中发生叶片断裂故障并击碎了蜗壳，造成停机，如图3所示。

图3 增压风机的离心式叶轮机及事故现场

为了追溯增压风机的离心式叶轮机发生叶片疲劳破裂的动态特征，对发生事故前采集的振动数据进行分析。在发生故障之前，设备运维人员定期采用振动传动器对机组进行振动测试，传感器的采集参数为fs=2 560 Hz，N=4 096。其中一段振动信号的时域波形及其傅里叶频谱如图4所示。压缩机的工作速度为744 r/min(对应于特征频率fc=12.4 Hz)。观察图信号的时域波形(图4(a))及其快速傅里叶变换频谱图(图4(b))可知：由压缩机工作速度造成的工频成分能量很大，非平稳故障成分不易进行观察。

采用中心极化多分辨分析对信号进行分解，在各子空间中没有观察到由叶片裂纹造成的故障特征。图5为子空间wp3，3(n)的时域波形及包络解调谱。采用笔者提出的稀疏共振解调算法对子空间信号进行处理。考虑到增压风机系统的转频，可将故障频率fc设置为转频12.4 Hz；梳形滤波器的带通半径RB设置为2Δf=2×4 096/2 560=1.25 Hz。使用的梳形滤波器表示为CF(12.4 s,1.25 Hz,3)。

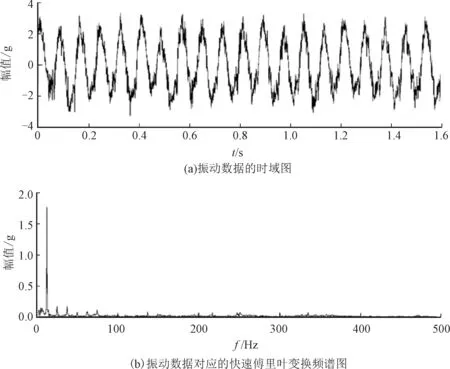
图4 振动数据的时域图和频谱图

对信号进行稀疏共振解调处理后的结果见图6。从图6中可以观察到以0.079 7 s为间隔的冲击成分，其对应的故障频率为12.54 Hz，与理论的故障特征频率12.4 Hz接近，因此可以确认该结果为叶片裂纹对应的故障特征。将图6中的时域波形与图5(a)进行对比，可以发现信号中的噪声干扰得到有效抑制。

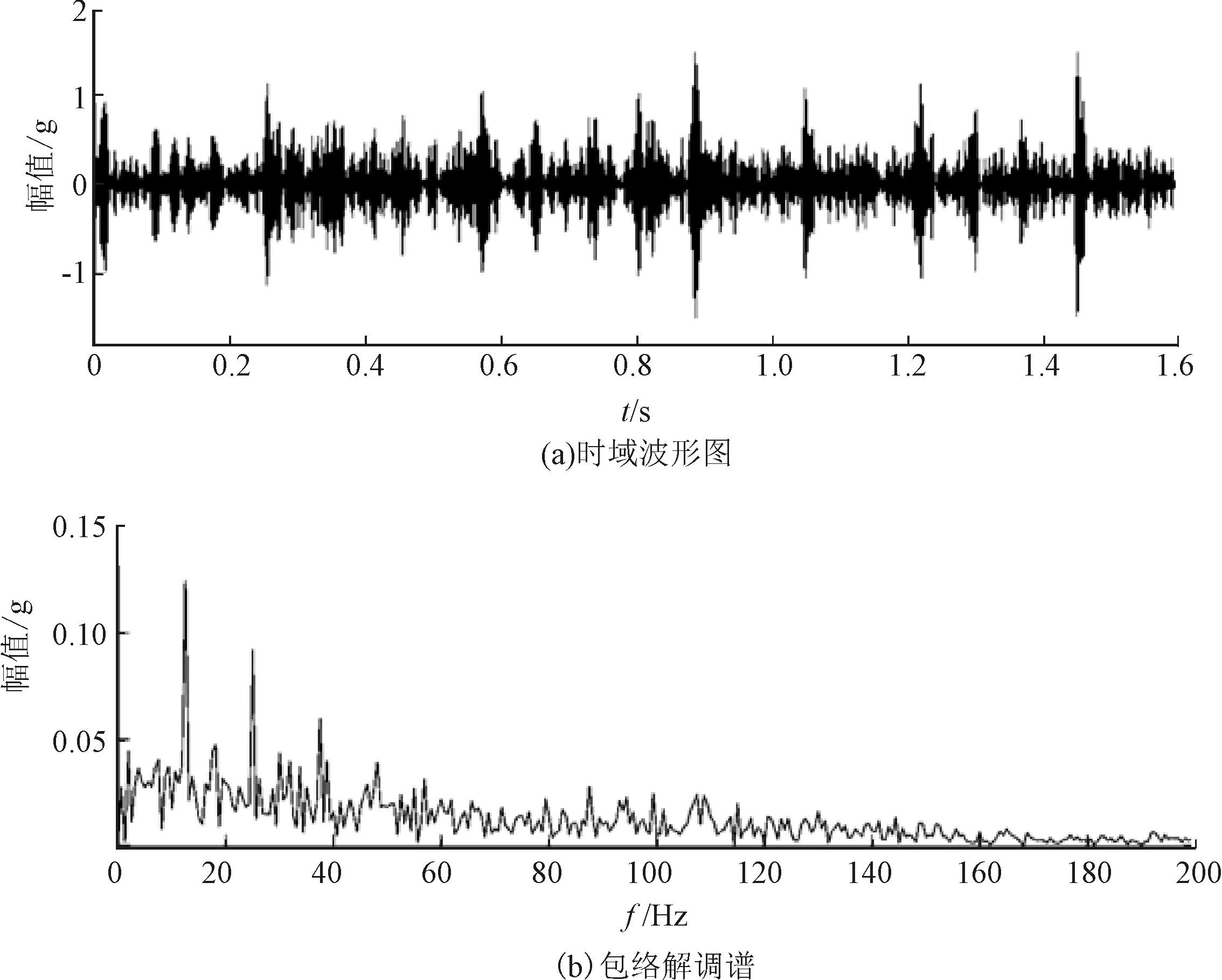
图5 子空间wp3,3(n)的时域波形图和包络解调谱

图6 子空间wp3,3(n)的稀疏共振解调结果

4 结束语

针对强噪声干扰振动测试信号中微弱周期性冲击故障特征的提取问题，笔者提出了一种稀疏共振解调方法。 该方法采用中心极化多分辨分析对动态信号中的多个分量进行解耦。中心极化多分辨分析通过围绕固定中心频率的多分辨分析，提高了频率-尺度网格上过渡带特征的提取能力。对于进入小波理论通带的强相干噪声，提出了包络解调域上的特征增强方法，利用梳形滤波器保留叶片故障的特征频率及倍频成分。最后结合包络解调曲线，参考模型曲线及子空间时域波形进行硬阈值降噪，得到稀疏共振解调结果。在某回收高炉煤气燃烧机组的增压风机上采集了振动信号，并采用所提出方法对该信号进行了分析，显著增强了振动信号中对应于叶片裂纹的微弱周期性故障特征的提取效果。