空间信息论的新研究进展

徐大专 罗 浩，2

（1.南京航空航天大学电子信息工程学院，南京，211106；2.江苏科技大学计算机学院，镇江，212003）

引 言

雷达、声纳和医学成像等目标探测系统可以从反射信号中获取目标的距离、方向和幅度等空间信息，正在国防和国民经济部门发挥越来越重要的作用。雷达探测的主要任务是目标的检测、估计和成像，除距离和散射信息之外，相控阵雷达和合成孔径雷达还可获得目标的方向信息，或者对观测区域进行成像。干涉合成孔径雷达甚至可以获得观测区域的三维空间信息。目前，雷达与通信技术相融合的趋势越来越明显，随着MIMO多天线技术在雷达和通信系统中的广泛应用[1-6]，雷达通信一体化技术[7-14]迅速发展，从共用天线、到共用射频、再到共用波形，融合的程度不断加深。雷达是一种典型的信息获取系统，而通信是一种信息传输系统，那么，雷达和通信两种信息系统能否在信息理论的基础上进行统一的描述和刻画呢？

空间信息论正是以香农信息论为基础，研究探测系统中目标空间信息问题的基础理论，这里的空间信息指被测目标相对于雷达的距离、方向和散射信息。空间信息论中“空间”这一名称是本文首次提出的，其意义与空间谱估计中“空间”一词的意义是一致的。

空间信息论所研究的基础理论问题可概括如下：

(1)空间信息的概念，即目标探测系统中，感知信息的本质是什么，怎样对空间信息进行严格的、科学的定义。

(2)空间信息的定量问题，即，空间信息的理论公式及闭合表达式。

(3)探测精度问题，即空间信息量与探测精度的关系问题。探测系统中，目标的参数估计精度是最基本的性能指标，空间信息论能否从信息论的观点解释估计精度问题。

(4)分辨率问题，即空间信息量与分辨率的关系问题。分辨率是目标探测系统特有的性能指标，空间信息论能否从信息论的观点解释分辨率问题。

近年来，作者的研究团队对空间信息论涉及的基本理论问题开展研究工作，并取得了一系列研究结果。针对上述基础理论问题，本文将给出本团队最新的研究成果。作者相信，空间信息论将形成新的基础学科，本文的工作当然是阶段性的，不可能对上述一系列基本问题给出全部答案。本文的研究工作中甚至还存在一定的错误，希望信息理论与雷达信号处理领域的学者共同探讨空间信息论这一新兴主题。

1 信息论在雷达探测系统中的前期研究工作

信息论与雷达的关系是国际学术界长期关注，而未能解决的基础理论问题。2017年，国际信息论期刊《Entropy“radar and information theory”》特刊的征稿启示[15]中写到：“自 Woodward和 Davies开创性地研究雷达信息理论的半个多世纪以来，信息理论已广泛应用于雷达信号处理中。然而，由于在雷达和通信领域中“信息”概念的内在差异，对雷达应用中信息理论的研究并不如其在通信领域中来的深入。雷达系统的唯一目的是寻找关于目标的信息，通常意义上是非合作的，而通信系统的目的是提取有关发射信号的信息。随后，Bell的开创性论文，即以信息论测度自适应地设计发射波形，进而从接收到的测量信号中提取更多的目标信息，使得信息论在雷达信号处理中重新站稳了脚跟。自此以后，信息理论准则，特别是互信息和相对熵（又称之为Kullback-Leibler散度），已成为自适应雷达波形设计算法的核心。”。该则启示充分表达了国际学术界开展“雷达与信息论”主题研究的迫切愿望！下面综述信息论在雷达系统中的主要研究工作及最新进展。

从Woodward＆Davies研究距离信息[16-19]至今已有近70年历史，特别是Bell的研究工作[20]发表后，以互信息和相对熵为测度进行雷达系统的波形设计引起了国内外学术界的广泛关注。近两年来，本项目组在雷达探测的空间信息理论方面也取得了部分研究成果。现将相关研究工作分述如下：

1.1 距离互信息

距离互信息的研究可追溯至20世纪50年代。针对单目标和幅度为常数条件下，Woodward和Davies[16-19]采用逆概率原理得到时延τ和散射系数α的联合后验概率密度

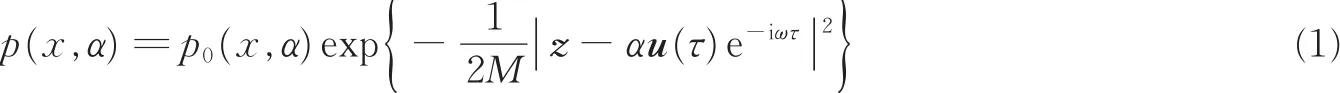
式中：p0(x,α)表示先验概率密度，u和z分别表示发射和接收的低频信号矢量，M为实噪声的平均功率。在此基础上得到了距离互信息与信噪比的近似关系

式中：ρ2表示平均信噪比，T表示观测时间长度，β表示信号的均方根带宽。

Woodward和Davies只研究了雷达探测系统中目标的距离信息问题，而没有涉及散射信息问题。而且，由于逆概率研究方法的局限，在他们的研究方向近70年以来没有取得进一步发展。

1.2 以互信息和相对熵为测度的雷达波形设计

1988年，Bell首先将互信息测度用于雷达系统的波形设计[20]，其系统模型如图1所示。其中，x(t)表示发射信号，g(t)表示目标冲激响应，回波信号z(t)是发射信号x(t)与目标冲激响应g(t)的卷积。z(t)叠加高斯白噪声n(t)，并经过匹配滤波器B(f)后得到信号y(t)。根据Neyman-Pearson准则，最佳目标检测的任务是设计发射信号x(t)和匹配滤波器B(f)，最大化信号y(t)和目标g(t)之间的互信息Imax(y(t)；g(t)|x(t))。Bell证明了最佳波形设计对应于信道容量的最优功率注水解[21]，即

图1 Bell的雷达目标信道模型Fig.1 Bell′s target channel model of radar

式（3）正好与通信系统的最优功率分配问题相吻合。

在Bell的系统模型中，目标的距离信息隐含于冲激响应g(t)中。由于实际环境中目标位置是不断变化的，因此，必须采用自适应的波形设计方法。由于Bell的工作是针对目标检测问题提出来的，其模型并不区分不同的目标，因此，从本质上说，Bell的工作只研究了空间信息中的散射信息问题，而没有涉及雷达探测系统中更重要的距离信息问题。

Bell的研究工作被进一步推广到不同雷达系统的波形优化设计中，但相关研究工作在本质上都不考虑距离信息。Leshem等[22-23]首先提出了一种针对单目标的频域波形设计方法，并进一步推广到多目标系统中。类似地，Setlur等[24]利用最大化幅度互信息测度，使得雷达系统可以从预先确定的波形集合中进行自适应选择。Wang等[25]针对常散射系数模型，建立认知雷达的幅度互信息表达式，并用于波形的自适应设计。根据Neyman-Pearson准则，相对熵（Kullback-Leibler散度）越大，目标检测器的性能越好。因此，相对熵及相关的互信息准则也被应用于雷达系统的波形设计。针对多基地雷达的目标检测问题，Kay[26]建立了假设检验的相对熵表达式，并在能量约束条件下，通过最大化相对熵对多基地雷达的发射信号进行优化设计。Sowelam等[27]通过最大化Kullback-Leibler散度，研究固定和变化两种不同的目标环境中雷达目标分类的波形选择问题。Zhu等[28]在有色噪声环境中，研究扩展目标检测时的最佳雷达波形问题，比较了输出信噪比、Kullback-Leibler散度和互信息3种现有波形设计度量之间的关系。针对基于假设检验的扩展目标识别问题，Xin等[29]利用相对熵准则研究信号相关干扰下的波形设计问题。

目前互信息准则也广泛应用与多载波和MIMO雷达等系统中。Sen等[30-31]研究了基于互信息准则的OFDM雷达波形设计问题。通过优化当前OFDM信号波形，使下一个脉冲状态矢量和测量矢量之间的互信息达到最大。在MIMO雷达中，Yang和Blum[32-33]研究与雷达波形设计相关的目标识别和分类问题。Yang等在传输功率约束条件下，以最大化随机目标冲激响应与反射波形之间的条件互信息作为波形设计准则，根据注水原理进行功率分配。他们发现，在相同的功率约束下，最大化互信息的设计方法同最小化均方误差所得到的优化波形相同。Tang等[34-36]进一步研究了MIMO雷达在有色噪声中的波形设计问题。他们分别采用互信息测度和相对熵测度作为最优波形设计准则。尽管两种最优解导致了不同的功率分配策略，但都要求传输波形与目标/噪声特性相匹配。Liu等[6]研究自适应OFDM雷达通信一体化系统波形设计，以提高频谱效率，解决了雷达的条件互信息和通信的信息速率的优化问题。Chen等[37]利用互信息准则研究自适应分布式MIMO雷达系统的波形优化问题，可以有效地改善目标检测和特征提取性能。

1.3 信息论在雷达信号处理相关领域中的应用

Paul等[38]建立了恒定信息雷达的模型和概念，并提出基于互信息准则的雷达目标调度算法。Talantzis等[39]利用互信息测度进行声学DOA估计，以两个接收传感器信号之间的互信息作为统计量提出了一种声学传感器中DOA估计算法。此外，信息论方法还被用于异常信号的检测[40-42]。

1.4 国内在信息论与雷达领域的研究工作

国内学者的研究工作主要集中在雷达波形设计方面。国防科技大学程永强教授团队[43-46]研究信息几何理论在雷达信号检测和信号处理中的应用。采用Kullback-Leibler散度对检测器及性能进行几何阐述，为雷达信号检测问题提供一种更全面的描述方法。针对认知雷达中多个扩展目标的波形优化设计问题，上海交通大学刘兴钊教授等[47]基于最大化接收回波的检测概率策略，通过引入附加权重向量提高了目标检测和估计的精度，结果表明与线性调频信号相比，基于最大检测概率和最大互信息准则，可以使雷达回波包含更丰富的多目标信息，从而提高雷达检测性能。哈尔滨工程大学齐琳等[48]提出基于信息熵和集成学习的调制信号识别方法，通过特征选择算法获得最优特征子集和最佳分类器。西安电子科技大学刘宏伟教授团队[49]针对扩展目标识别中距离敏感性的波形优化问题，在传统的注水原理基础上提出了特征互信息方法，通过最大化识别特征与目标特性之间的互信息提高目标的可分性。针对多个雷达目标的识别问题，国防科技大学廖东平等[50]研究基于互信息准则的认知雷达自适应波形设计方法，明显提高了多目标的识别性能。时晨光等[51-52]研究鲁棒雷达波形设计方法，在目标特征的互信息和通信系统的最小容量阈值约束条件下，通过优化OFDM雷达波形，最小化雷达发射功率。他们还利用互信息准则研究雷达网络中的低截获概率问题，并给出了波形优化设计结果。

1.5 作者研究团队在空间信息理论方面的研究工作

作者首次研究了雷达探测的距离信息和散射信息问题[53]。针对一般的雷达目标探测系统，建立了探测信息的理论公式，即雷达探测的距离信息量和散射信息量[54]，目标的散射系数为常数或服从瑞利分布。在高信噪比条件下，获得了散射系数为常数情况下距离信息的解析表达式。本文证明，距离信息量与雷达系统的时间、带宽和信噪比乘积的对数成正比，并且，距离信息上界与均方误差的克拉美罗下界是一致的。

针对阵列传感器，进一步研究信号的波达方向（Direction of arrival,DOA）信息和散射信息问题[55]，给出了阵列传感器场景下空间信息的定义，并推导出理论表达式和DOA信息的渐近上界。研究了非相关多源场景中，散射信息的信息量。提出了熵误差概念，用来作为性能指标评估传感器阵列的信息获取能力。

本文还研究了多载波雷达探测系统中信息量与最大似然估计的关系，设计了一种基于频域均衡和移相峰值搜索的最大似然估计(Maximum likelihood estimation,MLE)算法[56]。还研究了通用的多载波雷达目标探测系统的信息理论的分析框架，推导了距离信息、散射信息在恒模和高斯散射系数模型下的表达式，并给出了距离信息的近似解的闭式表达式，研究了距离分辨率的新的定义。

本文围绕空间信息论的基本问题论述了在空间信息论方面的研究工作，致力于建立目标空间信息的统一描述方法和空间信息论的理论框架，以期推动空间信息论在雷达信号处理领域的应用。

2 雷达目标探测系统

2.1 雷达目标探测系统模型

雷达目标探测系统模型如图2所示。

图2 雷达探测系统模型Fig.2 System model of radar detection

在图2中，ψ(t)表示发送的基带信号，当载波频率为fc，初始相位为φ0时，发射信号可以写为假设观测区间为[-D 2,D 2)，参考点是观测区间的中心，v表示信号传播速度，则时延范围为[-T 2,T 2)，T=2D v。考虑零均值，实部和虚部方差均为N02的复高斯加性白噪声信道，将接收信号下变频到基带，并通过带宽为B 2的理想低通滤波器，可以得到

式中：sl= αlejφl为第 l个目标的幅度模型，αl表示第 l个目标的散射系数，φl=-2πfcτl+ φ0为第 l个目标的相位，τl=2dlv表示第l个目标的时延，dl表示第l个目标与接收机间的距离，w(t)为带宽B 2的复高斯噪声。目标探测的目的就是从接收信号中获得目标的幅度、相位和距离信息，这样就与通信系统中的信道响应相类似，可以将雷达探测系统等效为一个信息传输系统，如图3所示。这里ψ(t)表示通信系统的基带信号，w(t)表示信道产生的复高斯噪声。雷达探测系统中目标散射模型s带来的散射信息等效于通信系统中调制基带信号的幅度和相位，而目标的距离信息则等效于通信系统中调制基带信号ψ(t)的时延τ。

图3 雷达探测系统等效通信系统模型Fig.3 The equivalent communication system model of radar detection system

为便于理论分析，假设雷达发射信号为理想低通信号ψ(t)=sinc(Bt),-T/2≤t≤T/2，其中，T表示观测时间。假设1/B≪T，即，信号能量几乎全部位于观测区间内。本文的分析结果也适用于线性调频信号和多载波信号。ψ(t)的带宽为B 2，本文以奈奎斯特采样率B对信号z(t)进行采样，采样序列为

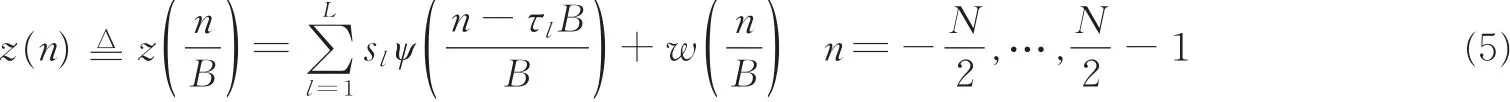
式中：N=TB称为时间带宽积(Time bandwidth product,TBP)。图4(a)表示目标在距离维上的探测范围，其位于探测范围的中点；图4(b)表示在时间维上目标的回波信号；图4(c)表示将带宽归一化后，目标的探测范围和离散回波信号。

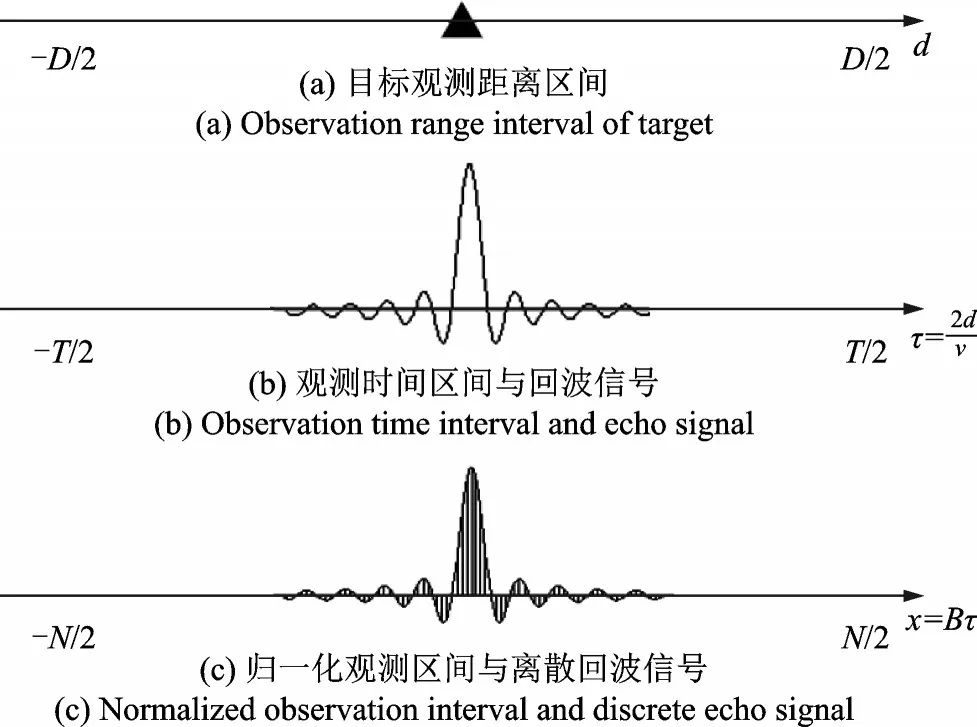
图4 3种观测区间与信号波形Fig.4 Three observation intervals and signal waveforms

接收信号z(t)能够完全由N点离散序列z(n)重建，且w(n)的采样值之间相互独立。令xl=Bτl表示第l个目标的归一化时延，式(5)可简化为

为了更好地表达和分析信号之间的关系，用X=[x1,x2,…,xL]T表示归一化时延矢量，则可写为矩阵形式

式(7)系统地描述了接收信号与目标的位置参数及散射信号之间的关系，在本文后面的分析中占有重要的位置。

2.2 空间信息的定义

雷达信号处理的目的是采用特定的方法或算法，从接收矢量Z中估计位置参数X和散射参数S。而空间信息论研究从接收矢量Z中获得的目标位置信息和散射信息，与具体的估计方法及算法无关。

设噪声是均值为0，方差为N0的复高斯白噪声，且各分量独立同分布，N维噪声矢量W的概率密度为

再由式(7)，给定目标距离x和散射信号s条件下，接收序列z的多维概率密度p(z|x,s)为

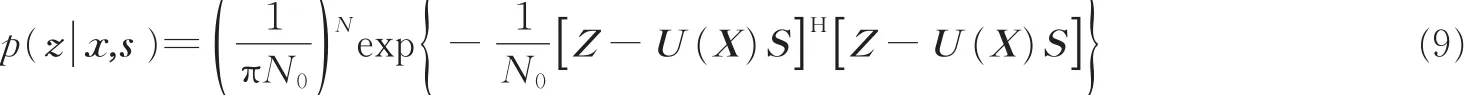
空间信息定义接收序列与目标距离X和散射S的联合互信息I(Z；X,S)，又称距离-散射信息，即

式中：E[·]为数学期望，并且有

由于目标距离x和散射特性s相互独立，故有p(x,s)=p(x)p(s)。

根据互信息的可加性原理

式中：I(Z；X)表示目标的距离信息，I(Z；S|X)表示距离已知条件下目标的散射信息。式（12）表明，研究空间信息可分为两个步骤，首先确定目标的距离信息I(Z；X)，然后在已知目标位置条件下确定目标的散射信息I(Z；S|X)。

一方面，Woodward和Davies只研究了雷达探测系统中单个目标的距离信息问题，即式(12)中的I(Z；X)，而没有涉及散射信息的问题，并且其方法无法直接推广到多目标场景。另一方面，Bell的研究工作以散射信息I(Z；S|X)最大化为目标进行雷达系统的波形设计，以提高目标检测的性能。Bell的研究工作把雷达探测系统等效为一个多径信道（并不需要知道目标的位置），这样I(Z；S|X)最大化等效于通信系统中在发送端进行功率分配（波形设计），使信道容量最大化。由于实际中探测目标位置的变化，雷达波形设计是自适应的，正如，通信系统需要不断进行信道估计和反馈，进行自适应功率分配一样。与通信系统的不同之处在于，雷达可以直接从目标反射信号中估计信道状态信息，而不需要反馈信道提供信道状态信息。以上分析表明，Bell的工作并没有涉及雷达探测的距离信息问题。

(1)目标散射模型

在此类问题中，对于目标散射统计模型，主要考虑和研究Swerling 0和Swerling 1两种模型。

（a）Swerling 0模型

非起伏，回波信号的功率恒定，雷达和目标都处于完全静止的状态，目标模型建模为恒模散射系数模型，目标的相位φ，建模为区间[0,2π]上均匀分布的随机变量，概率密度可以表示为

通常雷达系统的工作频率非常高，微小的时延将导致相位的巨大变化。因此，视φ为[0,2π]上均匀分布随机变量是合理的。

（b）Swerling1模型

具有许多随机分布的散射体，且没有占主导作用的强散射体。散射系数幅度服从瑞利分布，概率密度可以表示为

相位服从均匀分布，在这种情况下，S可被建模为复高斯矢量。

假设目标间的散射是不相关的，目标相位矢量Φ=[φ1,φ2,…,φL]T的先验概率分布可建模为

式中：p(φl)=12π，l=1,2,…,L。

(2)目标位置的先验统计模型

对于目标位置距离的统计模型，假设目标在观测区间上相互独立，并服从均匀分布，则距离参数x的先验概率分布为

3 单目标探测系统的空间信息量

针对单目标探测系统，可得在给定α，x和φ的条件下，z的多维概率密度函数为

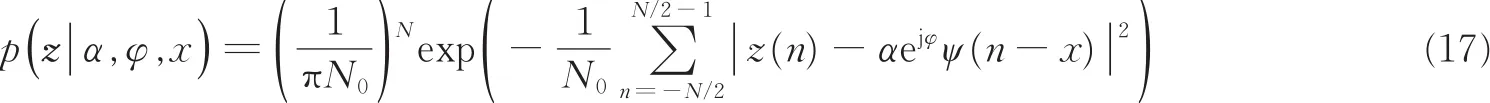
在该模型中，以上的概率密度函数定义了一个多参数调制的通信信道，这样，雷达探测的空间信息就等效于该多参数调制通信系统传输的信息量。

3.1 距离信息量的理论公式

目标的距离信息I(Z；X)的理论表达式可表示为

式中：h(X)为目标距离的先验信息，h(X|Z)为目标距离的后验信息。那么单目标探测下的距离信息量I(Z；X)为

(1)恒模散射目标

假设目标的归一化时延为x，目标的散射系数的模α为常数；如果噪声为复高斯分布，那么在给定x,φ的条件下，接收矢量Z的多维概率密度函数为

由贝叶斯公式，已知接收信号Z条件下目标位置X的后验概率密度为[53]

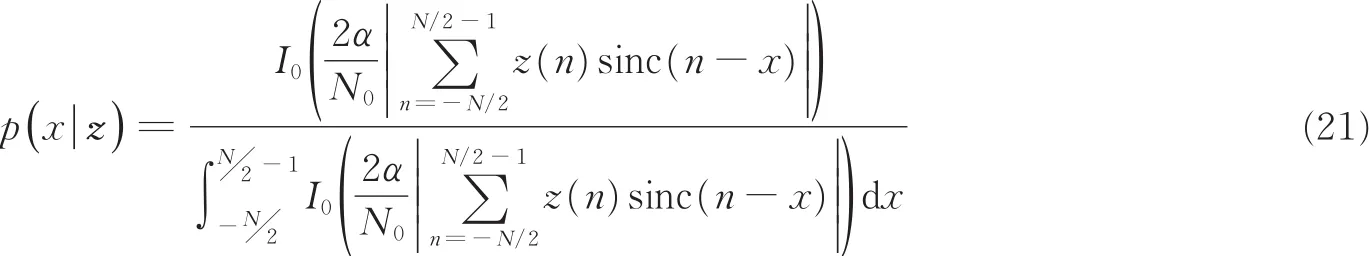
式（21）也称为似然函数，其中I0(·)表示第1类零阶修正贝塞尔函数，代入式(19)即可求出恒模散射目标的距离信息量。

在高SNR条件下可以证明位置x的后验概率密度近似为高斯分布，即

式中：σ2=(ρ2β2)-1表示目标估计的均方误差，信噪比ρ2定义为发射信号能量归一化时，回波信号的能量εs和复高斯噪声实部功率的比值ρ2=εs/(N0/2)，从而得到恒模散射目标距离信息I(Z；X)的上界为

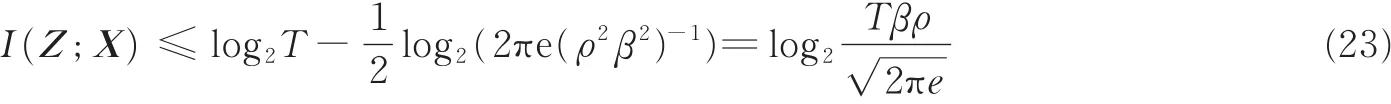
以时间带宽积为参数，距离信息与信噪比的关系如图5所示。可以看出，距离信息与时间带宽积N=TB的对数成线性关系，并随着信噪比的增大而增大。图5中的虚直线是距离信息的上界。

可以从空间信息论角度来解释雷达目标探测过程。如图5所示，当SNR较小时，由于噪声的影响，距离信息很小，无法发现目标。当SNR超过0dB之后，距离信息随着SNR以较大的斜率增加，距离信息描述雷达探测的两个重要的阶段，即目标捕获阶段和目标跟踪阶段。在目标捕获阶段，距离信息每增加1bit，意味着目标的观测区间缩小为原来的一半。当距离信息等于log2TB时，观测区间达到1TB，即达到了雷达系统的距离分辨率1B；在目标跟踪阶段，通过相干累积可以大幅提高信噪比，这时，距离信息与时间带宽积的对数呈线性变化，且随着信息量的增加，观测精度越来越高，从而突破带宽分辨率1B的限制。

(2)复高斯散射目标

针对高斯散射目标，给定接收矢量Z条件下目标位置X的后验概率密度为

图5 不同时间带宽积下恒模散射模型的距离互信息与SNR的关系Fig.5 Relationship between range information and SNR for constant module scattering model at different time bandwidth product configurations

式中：ρ-2=1/ρ2，由于在复高斯散射场景下，散射系数是随机变量，则ρ2定义为目标的平均信噪比。然后将p(x|z)代入式(19)即可求出复高斯散射目标的距离信息量。

图6是恒模散射目标和复高斯散射目标的距离信息量对比曲线，时间带宽积N=32。从图6可以看出，在高信噪比（20dB以上）条件下，高斯目标的距离信息上界低于恒模目标，这是因为，即使平均信噪比很高，复高斯目标也存在大量小信号样本，从而影响平均距离信息量。

为了获得复高斯目标距离信息量的上界，将信噪比看作指数分布的随机变量，方差为2ρ2/N0，其上界为

式中γ=0.5772156…为欧拉常数。

高斯散射目标与恒模散射目标距离信息量上界的比较如图7所示，可见，高斯目标距离信息量上界比恒模散射目标低0.416bit，换句话说，达到相同信息量时信噪比相差约2.5dB。

图6 恒模和复高斯散射模型的距离信息量Fig.6 Range information of constant module and complex Gaussian scattering model

图7 恒模和复高斯散射模型的距离信息量上界Fig.7 Upper bound of range information for constant module and complex Gaussian scattering model

3.2 距离信息的闭合表达式

距离的概率密度由信号的自相关、信号与噪声的互相关两部分决定。恒模散射目标距离信息的闭合表达式通过归一化方法进行近似计算。p(x|z)的数值集中在目标所在的位置x0附近，因此在计算微分熵时对x积分的区间可以划分为信号区间和噪声区间。从而距离信息近似为

式中：Hs和Hw分别为高、低信噪比情况下的后验熵。高信噪比情况下p(x|w)近似服从方差为σ2=(ρ2β2)-1的高斯分布

低信噪比情况下，可以得到噪声部分的熵

式中ps为准确度，表达式为

值得注意的是，当信噪比足够低，可以认为积分区间内只有噪声，此时不确定性达到最大。这意味着获得的距离互信息在这种情况下趋于零。式（29）具有明确的物理意义，距离信息理论公式的数值结果和近似解如图8所示。结果表明，得到的近似解在整个信噪比区间和理论结果吻合较好，明显优于Woodward结果。

图8 距离信息的理论解和近似解N=128Fig.8 Theoretical and approximate results of range information with N=128

3.3 目标的散射信息

在获取目标位置的条件下确定目标的幅度和相位信息I(Z；S|X)，可得

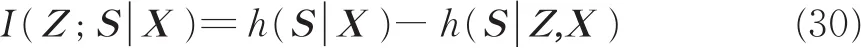
式中：h(S|X)和h(S|Z,X)分别是在位置已知时，目标散射的先验和后验信息。

(1)恒模散射目标

考虑散射信息 I(Z,S|X)就等同于相位信息 I(Z,Φ|X)，通过求解 p(φ|z,x)和 p(φ|w,x)，可以得出目标的相位信息为

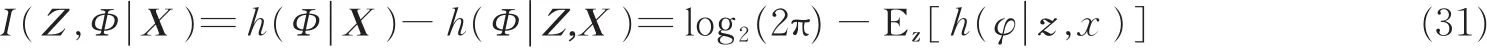
(2)复高斯散射目标

当目标为复高斯散射时，即目标的散射系数服从瑞利分布，且相位服从均匀分布时，目标幅度Y可以被认为是复高斯变量。在估计得到了目标的位置之后，信号矩阵u(x)为常数矩阵，并且噪声矢量W为独立的高斯分布，由此可知Z也是一个高斯矢量。则在X=x时，散射信息为

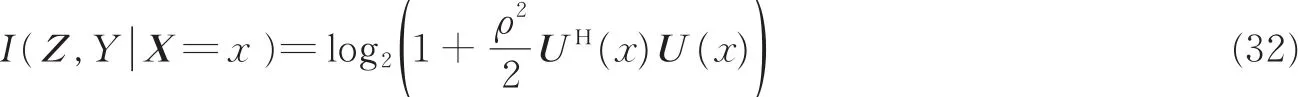
另外，对于观测区间x∈[-TB 2,TB 2]，考虑其长度远大于u(t)的能量区域，当N足够大时，有UH(x)U(x)≈1，从而可以得到

式（33）意味着I(Z,Y|X=x)与目标估计的归一化时延无关，也就是说，在复高斯散射场景中，目标的散射信息与距离信息无关。

散射信息量公式在形式上与Shannon信道容量公式一致。这一结论并不是偶然的，因为，雷达目标探测系统可以等效于一个时间-幅度-相位联合调制系统，给定位置信息等价于系统处于完全同步状态，这时单个高斯信源符号通过加性高斯白噪声信道的互信息即为香农信道容量。以上分析表明，在同步条件下，通信系统传输的信息在本质上就是散射信息，而不存在时间信息。

恒模散射目标和复高斯散射目标两种情形下，对应的散射信息仿真曲线如图9所示，可以看出散射信息与信噪比成正比关系，随着信噪比的升高而增加，且复高斯散射目标比恒模散射目标获得的信息量要大。两者的差值就是恒模散射目标下散射信息退化为相位信息所减少的信息量。

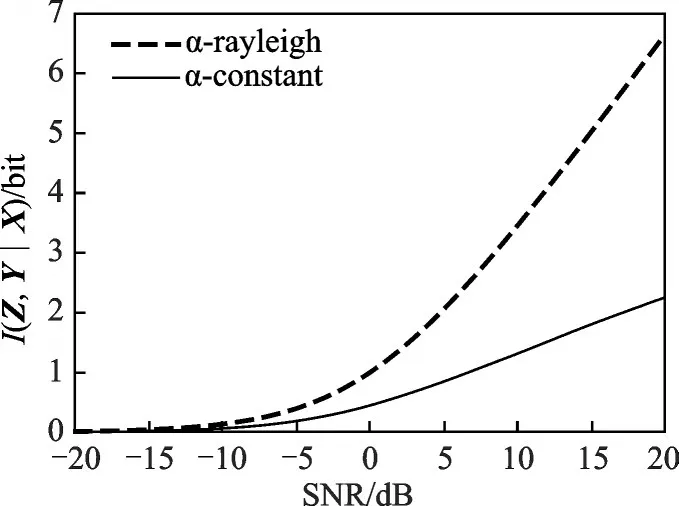
图9 散射信息量与信噪比的关系曲线Fig.9 Scattering information versus SNR

4 多目标探测系统的空间信息

在多目标雷达探测场景中，雷达天线发射信号并接收多个目标反射的回波信号，从回波信号中获取目标的位置和状态信息。

4.1 多目标的距离信息

针对更一般的多目标场景，其距离信息量的理论公式为

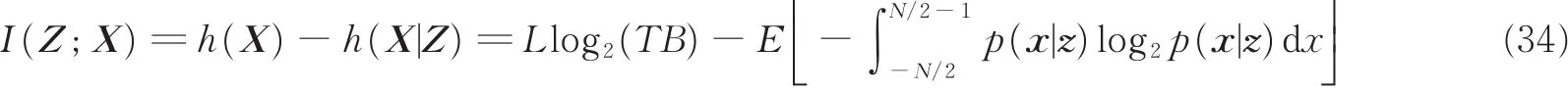
多目标距离信息的闭合表达式尚未发现，距离信息量通常由仿真或数值计算得到。

(1)复高斯散射目标

首先讨论复高斯散射目标的情况，接收矢量Z也是复高斯的，其协方差矩阵R为

复高斯散射多目标的距离信息的后验概率公式可以表示为

从而由多目标的距离信息的理论表达式可得多目标的距离信息。

复高斯散射情况下，以时间带宽积TB为参数，远距离两目标的距离信息量如图10所示。当信噪比较小时，噪声干扰较大，距离信息量很小。随信噪比增加，距离信息量迅速增加，且TB越大，获得的信息量越多。

以信噪比为参数，两目标距离信息量随距离差的关系如图11所示。当距离差较小时，目标相互干扰较大，获得的距离信息较小，在两目标重合时达到最小值。随距离差增大，获得的联合信息量变大，最后在两目标距离足够远时，目标互不干扰，获得的信息量趋于平稳。

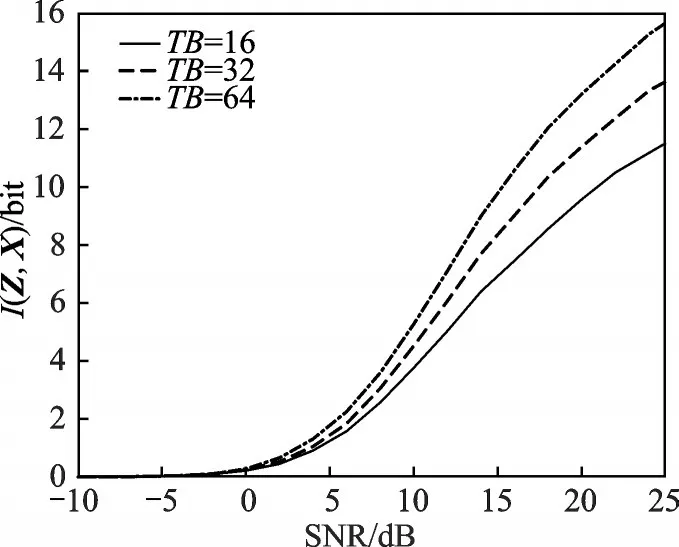
图10 远距离两目标的距离信息量（复高斯散射系数目标）Fig.10 Range information of two targets at a long distance(complex-Gaussian scattering model)

图11 两目标距离信息与距离差的关系（复高斯散射系数目标）Fig.11 Relationship between range information and distance difference for two targets(complex-Gaussian scattering model)

(2)恒模散射目标

而对于恒模散射目标的情况，概率密度表示为

类似地可由式(34)得到多目标的距离信息。

而作为多目标的一般情形，研究两个目标的距离信息的理论表达式。可以利用SVD分解转换信号空间，可求得后验概率密度p(x|z′)，其中z′=Sz。最终可以由多目标的距离信息的定义求得两个目标的联合距离信息。

4.2 多目标的散射信息

在获取目标位置的条件下确定目标的幅度和相位信息I(Z；S|X)，由于恒模散射情况较为复杂，仅介绍复高斯散射多目标的情况。由于Z是一个协方差矩阵为R的高斯矢量，那么当L个目标足够远时，雷达探测系统的散射信息为

式（38）表明，多个复高斯散射目标在距离间隔较大时，散射信息等于各个目标散射信息之和，而与距离信息无关。

可以得到两目标散射信息的闭合表达式。给定目标位置X时，且假设每个目标的具有相同的信噪，雷达系统等价于2×N的MIMO信道，根据MIMO信道容量公式

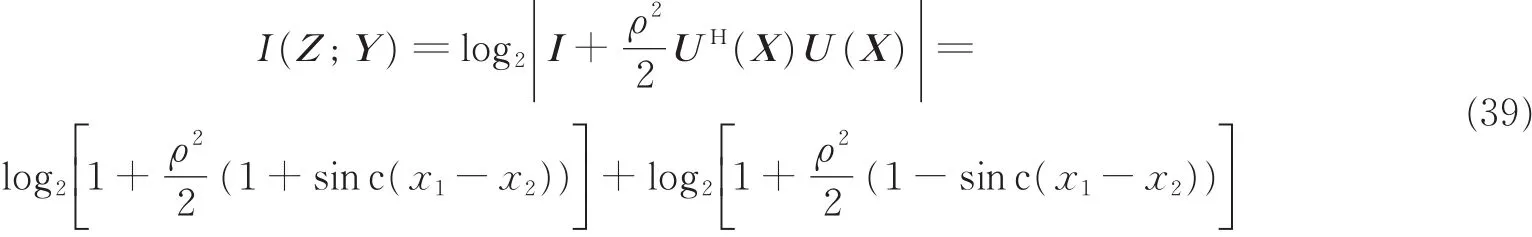
两目标状态服从复高斯分布且互不干扰的情形下，对应的散射信息仿真曲线如图12所示。可以看出散射信息随着信噪比的增大而增加，且为单目标时的两倍。为分析两目标距离对散射信息的影响，信噪比分别取15，20，25dB，两目标散射信息量随距离差的变化关系如图13所示。当距离差较小时，目标相互影响，获得的散射信息较小，在两目标重合时达到最小值。随距离差增大，获得的散射信息量变大，最后在两目标距离足够远时，目标互不干扰，获得的散射信息量趋于平稳。

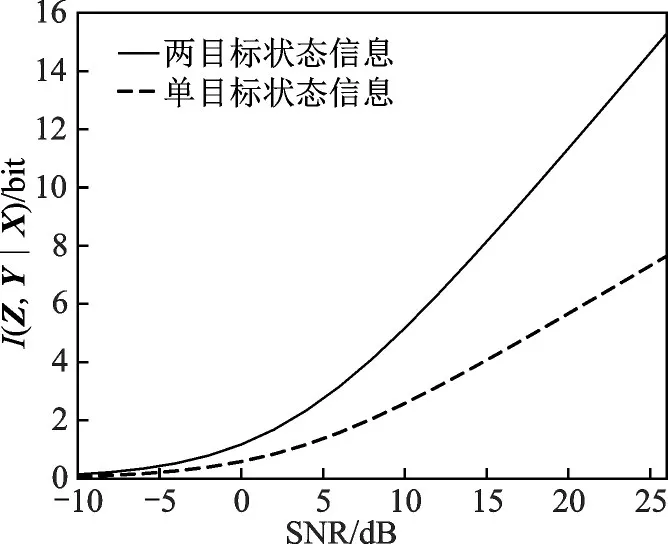
图12 远距离两目标的散射信息量（复高斯散射系数目标）Fig.12 Scattering information of two targets at a long distance(complex-Gaussian scattering model)

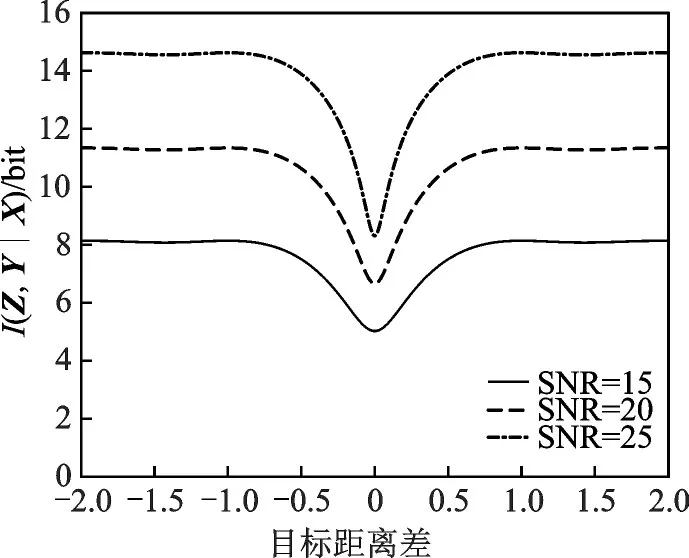
图13 两目标散射信息与距离差的关系Fig.13 Relationship between scattering information and distance difference for two targets

5 熵误差与目标探测系统的性能评价

空间信息量与雷达探测系统存在着本质的联系。为了从信息论的角度评价探测系统的性能，将后验分布的熵功率定义为熵误差(Entropy error,EE)，即

式中：h(X/Z)是已知接收数据Z的后验熵，其不确定性反映了雷达系统的探测性能。事实上，熵误差是均方误差的推广。在高信噪比条件下，后验概率分布逼近高斯分布，因此

熵误差逼近均方误差。在中低信噪比时，熵误差则是均方误差的下界。

熵误差的平方根称为熵偏差。熵偏差也是衡量雷达探测性能的重要指标，容易证明互信息I(Z；X)熵偏差之间满足

式（42）清楚地揭示距离信息量与探测精度的关系，即，每获得1bit信息量等价于熵偏差减小一半，或熵误差减小6dB。

为了更清楚地说明熵误差和熵偏差在雷达探测系统性能评价方面的重要意义，对熵误差和均方误差作进一步比较。

（1） 高斯-均匀混合分布的熵误差和均方误差

为比较熵误差和均方误差，构造一个高斯-均匀混合分布。设g(x)为高斯分布N(0,σ2)，为观测区间T上的均匀分布U(-T/2,T/2)，称目标位置估计的后验概率分布(Posterior probability density function,PDF)

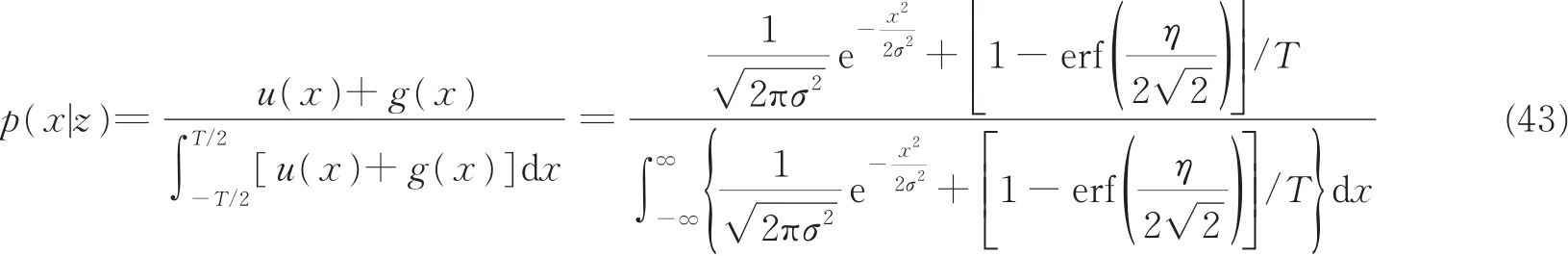
为高斯-均匀混合分布，如图14所示，其中，η=T/σ2称为高斯混合因子。

高斯-均匀混合分布的物理意义如下：假设目标位置估计总体上服从高斯分布，但在有限的观测区间上，高斯分布不满足概率的归一化条件。为此，引入均匀分布对高斯分布进行修正。高斯混合因子越大，表明信噪比越高，目标位置估计的精度越高，高斯分布的占比越大，后验概率分布越接近高斯分布。高斯混合因子越小，表明信噪比越低，均匀分布的占比越大，后验概率分布越接近均匀分布。

熵误差、均方误差与η的关系如图15所示。注意到，高斯因子η越小，方差σ2越大，对应于低信噪比情况，此时归一化概率密度越趋近与均匀分布。而当η越大，方差σ2越小，对应于高信噪比情况，此时归一化概率密度越趋近与一个高斯分布。在高信噪比情况下，熵误差和均方误差趋于一致。

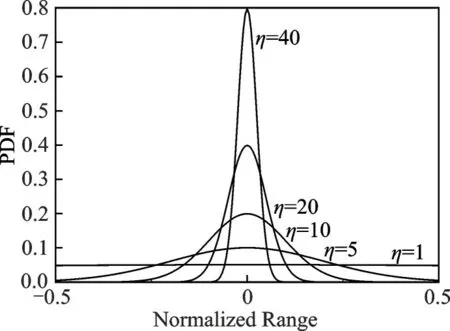
图14 高斯-均匀混合分布归一化概率密度函数Fig.14 Normalized probability density function of Gaussian-Uniform distribution

（2） 空心分布的熵误差和均方误差

假设目标位置的估计服从一空心分布，即目标仅在两端Δ/2范围内等概率出现，如图16所示。那么，概率密度可以表示为

而均方误差等于

图15 熵误差、均方误差与高斯混合因子的关系Fig.15 Entropy error,mean square error versus Gaussian Mixture factor

图16 空心分布模型图Fig.16 Diagram of hollow distribution model

空心分布的均方误差和熵误差如图17所示。Δ越小，获得的关于目标位置的信息应该越多，而从图17中看出，在Δ比较小的情况下，MSE却变得越大，已完全不能反映目标位置估计的性能。而熵误差则随着Δ变小而变小，这与直观上的理解一致。

虽然空心分布在参数估计领域并不常见，但常见于许多学习和认知场合。

以上分析表明，熵误差是比均方误差更好的性能度量指标，因为均方误差是二阶统计量，更适合误差分布接近高斯分布的远景，而在中低信噪比条件下，均方误差逐渐失效。

（3） 克拉美罗界和熵误差的关系

克拉美罗界（Cramér-Rao bound，CRB）是衡量参量无偏估计的一个重要指标，是指通过估计随机参量所能达到估计值的最小均方误差。根据上述模型，可以得到恒模和复高斯散射目标模型的归一化时延x0的无偏估计x的CRB为

图17 空心分布中均方误差和熵误差之间的关系Fig.17 Relationship between mean square error and entropy error in hollow distribution

并且，由恒模散射目标距离信息上界式(21)，可计算对应的熵误差下界

同理，由复高斯散射目标距离信息上界式可计算对应的熵误差下界

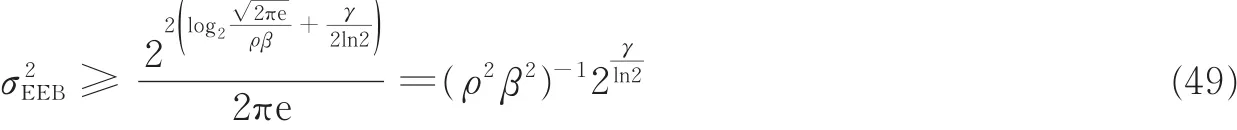
以恒模散射模型为例，距离信息的熵误差、均方误差和CRB如图18所示，在低信噪比情况下，熵误差的性能优于均方误差。在高信噪比区域，熵误差与均方误差估计的误差一致，接近克拉美罗界。

6 空间信息与雷达目标分辨率

雷达分辨率是雷达探测系统的重要指标，目前的结论是雷达分辨率等于1/B，系统带宽越大，分辨率越高。一个重要的基本问题是，空间分辨率与雷达分辨率有什么关系，能否从空间信息角度定义分辨率。

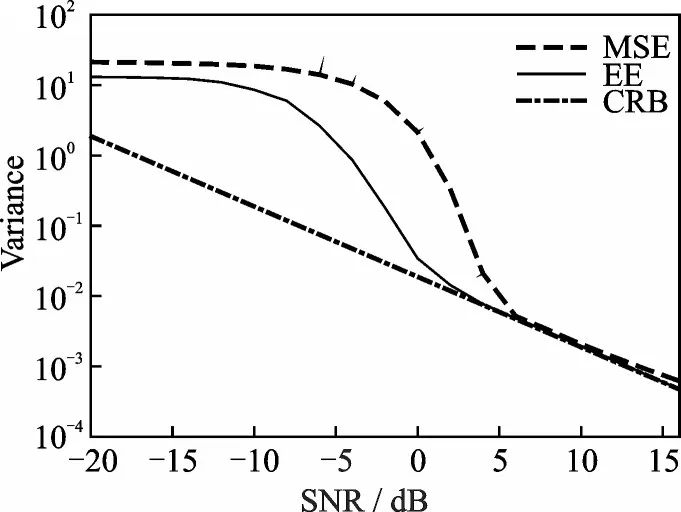
图18 常数模型距离信息的EE、MSE和CRBFig.18 Entropy Error,Mean Square Error and CRB of range information for constant module model

针对两个高斯散射目标，由散射信息表达式(39)，其散射信息由两部分组成，分别对应于信号空间的两个奇异值。将第1项较大的信号称为同相信号分量，第2项称为正交信号分量，而正交分量的散射信息 l反映了两个近距离目标的可分辨程度。若目标之间的距离越远，获得的信息量越大，越容易分辨；反之，获得的信息量越小，越难以区分。

式中：ρ表示平均信噪比的平方根，假设每个目标具有相同的信噪比ρ21=ρ22=ρ2。式（50）定义的分辨率不仅与系统带宽有关，而且与信噪比有关。信噪比越大，可分辨目标间隔越小，分辨能力越高。

从空间信息角度定义的分辨率与传统的1/B分辨率不同，可随信噪比的增加达到任意小。由于式（50）定义的分辨率在形式上与克拉美罗界类似，故本文称之为CR分辨率。那么，CR分辨率与1/B分辨率是否矛盾呢？本文认为CR分辨率与1/B分辨率并不矛盾，其原因是，在两目标时，分辨率问题本质上是两维匹配滤波问题，而传统的分辨率是将两维匹配滤波问题简化为一维匹配滤波问题。

采用两维最大似然算法来仿真两目标分辨率问题，两维最大似然算法区别于一维最大似然，将目标1的距离搜索和目标2的距离搜索放在两个维度，进行两维峰值搜索，从而得到概率分布，能够更加清晰地分辨出两个目标。

图19是针对不同距离差的两个临近目标，利用理论后验概率分布p(x|z)和最大似然算法，在不同信噪比下分辨目标的仿真图。可以看出，此方法能区分1B内的两个目标，但是随着目标间距离越加接近，越难分辨出两个目标。不过在同等情况下，改善信噪比能继续分辨出目标。理论分析和数值仿真结果表明，从信息论角度定义的CR分辨率，更具一般性和合理性。

7 传感器阵列的空间信息

传感器阵列是一组以某种几何图案部署的传感器，通常用于收集和处理电磁或声学信号。传感器阵列优点在于为观测提供方向性维度，有助于估计更多参数并提高估计性能。传感器阵列信号处理的核心是融合在几个传感器处收集数据的能力，以便提取信号特征并解释信号中包含的信息。

图19 不同信噪比分辨临近目标Fig.19 Distinguish adjacent targets under different SNR

7.1 传感器阵列的系统模型

传感器阵列系统模型如图20所示，由M个接收阵元按间距d均匀排列构成。

同时设有K个具有相同中心频率ω0的远场信源分别以来向角θ1,θ2,…,θk入射到该阵列，则第m个阵元的接收信号表示为

图20 均匀线阵模型Fig.20 Model of uniform linear array

式中：si(t)表示投射到阵列的第i个源信号；wm(t)为第m个阵元的复加性高斯白噪声；τm(θi)为来自θi方向的源信号投射到第m个阵元时，相对于选定参考点的时延。电波从点辐射源以球面波向外传播，只要离辐射源足够远，在接收的局部区域，球面波就可以近似为平面波。雷达和通信信号的传播一般都满足这一远场条件。

如用矩阵描述，并忽略这里时间t对S的影响，阵列信号模型可表示为

7.2 传感器阵列的空间信息

传感器阵列的系统模型与雷达探测系统模型具有高度的相似性，源的波达方向对应于目标的距离，方向矩阵对应于波形矩阵。可以类似地定义传感器阵列的空间信息为方向-散射联合信息I(Z；Θ,S)，并且

因篇幅所限，关于传感器阵列的空间信息的分析参见文献[55]。

8 结束语

空间信息的本质源于目标的不确定性。本文从香农信息论的观点出发，给出空间信息的定义，并推导出空间信息量理论公式。可以用比特为单位度量雷达等目标探测系统获得的信息量，这样，信息获取系统和信息传输系统可以统一在香农信息论的基础上。

在单目标情况下，得到距离信息和散射信息的闭合表达式。多目标的空间信息问题非常复杂，只有在一些特殊条件下才能得到闭合表达式，一般情况的空间信息量只能通过数值计算或计算机仿真。空间信息量不依赖于具体的参数估计方法，可以作为理论极限，为实际参数估计算法提供比较的依据。例如，在高信噪比场景，克拉美罗界提供参数估计误差的理论下界，但中低信噪比条件下，各种参数估计的最佳性能尚不可知。而距离信息量，也就是熵误差则可以为各种信噪比场景提供估计误差的理论下界。

本文定义的熵误差比均方误差具有更广泛的适用性。熵误差在高信噪比时退化为均方误差，在中低信噪比时熵误差优于均方误差。雷达探测系统获得1比特信息量意味着熵偏差减小一半，或探测精度提高一倍。空间信息论定义的熵误差/熵偏差为评价信息获取系统性能提供了一个崭新的视角。

本文提出的CR分辨率不同于传统的1/B分辨率，可以随信噪比的增加而达到任意的程度。作者采用两维匹配滤波方法验证超过1/B分辨率的可能性，这一结论为超分辨参数估计和雷达成像技术提供了新的理论依据。

目前，空间信息论仍然存在许多重要的理论问题亟待解决，例如：

（1）本文的研究工作针对单天线雷达探测系统的距离-散射信息和传感器阵列的方向-散射信息，怎样推广到复杂的阵列探测雷达系统、光学成像系统、医学成像系统、甚至更复生物视觉信息获取系统都是非常有意义的。

（2）对于空间信息的主要研究工作针对单目标和特殊的多目标场景，一般的多目标空间信息问题极其复杂，需要进一步研究。

（3）熵误差和CR分辨率指出理论极限，但这些理论极限的可达性问题尚未解决。该问题类似于香农的编码定理问题，亟待进一步研究。

以上研究工作表明，空间信息论在雷达等目标探测领域具有重要的理论意义和应用价值。空间信息论作为一个新兴的基础理论课题，目前正处于不断发展和完善的阶段。作者相信，随着空间信息论研究的不断深入，将突显对雷达信号处理技术的推动作用。