小波变换在某气田地震剖面滤波中的应用

刘佳宾，王四巍，王艳艳，丁 聪，陈钧龙

(1.华北水利水电大学岩土工程与水工结构研究院, 郑州 450046;2.河南省岩土力学与结构工程重点实验室，郑州 450046；3.河南省交通规划设计研究院股份有限公司，郑州 451450)

0 引言

噪声压制是地震勘探资料成像处理的重要环节，噪声压制效果是决定最终成像效果的关键因素之一。最早被人们使用的地震信号数字滤波方法是傅里叶变换[1]，该方法通过将地震信号由时间域转换至频率域，建立合适的滤波器，滤去干扰波的频谱成分，然后反变换至时间域来实现去噪目标。1946年，Gabor.D[2]提出了短时傅里叶变换方法，目前该方法仍被广泛使用。但是傅里叶变换在频率域的分辨率与时间域的分辨率二者互相制约：时间分辨率与频率分辨率二者不能同时任意提高。傅里叶变换是针对平稳信号进行的时频分析，对于地震信号这样的非平稳信号，傅里叶变换只能给出整体信号中包含的某一频率分量的平均值，不能完整把握信号在某一时刻的本质特征，因此严重制约了该方法精度。信号在时频联合平面上具有多个不同的能量聚集区域，这种信号称之为多分量信号，即时频面上的每一个分量对应一个信号分量。1948年，J.Ville[3]把Wigner分布引入非平稳信号时频分析领域中，该方法的优点在于不需要受到窗函数的制约，但是在处理多分量信号时，会出现交叉项，并不适用于复杂地震信号[4]。1982年，Morlet J.[5]提出了一种新的时频分析方法即小波变换。该方法通过选择尺度因子与平移因子，根据信号的特点对时窗进行调整，可以在信号的不同位置提供不同的分辨率。该方法在滤波过程中可以对信号的局部特征进行更好的识别，更准确地区分有效信号和噪声，取得更好的滤波效果。段春节等人[6]将小波变换方法与相干体技术相结合，提出了一种基于小波变换的相干体计算的新方法，得到突出特定频带的相干体。吴雅娟等人[7]通过改进的小波阈值法在有效滤除测井信号中的噪声的同时，又可以保留曲线的细节信息。

小波变换方法自20世纪90年代，C.S.Luchele等人[8]利用小波分析刻画地质体的不均匀性；高静怀[9]采用解析小波的方法求取地震信号的瞬时参数，深入地分析了不同尺度下地震记录小波变换结果及其对应的瞬时参数含义。王姣等人[10]针对互补集合经验模态分解(CEEMD)舍弃高频分量的去噪方法和小波阈值去噪方法存在的不足，利用小波阈值去噪方法对地震信号进行滤波。王江涛[11]基于小波多尺度的分析技术，提出了基于小波分析的动态变形信息提取多尺度分析方法,并应用于强噪声背景下提取弱信号及信号的奇异性检验，有效提取了动态变形信息。阮清青[12]通过对修正S变换与常规时频分析方法的对比，根据合成信号以及实测地震记录的时频分析得知修正S变换较常规的时频分析方法具有更好的时频分辨率和能量聚集性。

显而易见，小波变换已广泛应用于地震数据压缩、地震数据特征的分析、以及多尺度反演等领域，且其处理效果主要依赖于小波基函数的选择。本文通过实例对地震信号不同小波基函数的滤波效果进行比对，讨论小波基函数的选取，并采用二维小波包滤波分析方法对地震剖面进行处理，验证滤波效果。

1 小波变换滤波方法

1.1 小波变换原理

小波变换是采用待处理信号的一组基本小波函数在空间上的投影对信号进行描述。由不同尺度因子(a)与时移因子(b)构成的小波基表达式如下：

(1)

式中Ψ(t)表示某类小波基函数，上式须满足a≠0。

使用连续小波变换(CT)把信号x(t)映射到时间—尺度平面：

(2)

式中Ψ*(t)表示某类小波基函数的共轭表达式。

(2)式的逆变换为：

(3)

式中，CΨ是小波的容许性条件，即当CΨ满足下式(4)时，可以由小波变换的结果重构原始信号。

(4)

其中Ψ(w)为Ψ(t)的傅里叶变换。

通过改变小波基的尺度因子，可以改变其对所处理信号的分辨率。当遇到低频信号时，増大小波函数在时间上的尺度，降低被处理信号的时间分辨率，从而达到提高其频率分辨率的目的；遇到高频信号时，缩小小波函数的时间尺度，使之具有更高的时间分辨率，更好的表述信号的高频部分。本文采用二尺度分解的方法，首先将待处理的地震信号S分解为高频(d1)与低频(a1)两部分,然后对低频(a1)部分再次进行分解，得到高频(d2)与低频(a2)分量。此时原始信号S等于a2、d2与d1之和，对转换至小波域的地震信号进行阈值处理即可达到滤波的效果。小波域中较小的小波系数主要包含的是随机噪声，所以对较小的小波系数进行压制后，即可重构得到压制噪声之后的信号。

1.2 小波变换滤波原理

阈值去噪简而言之就是对信号进行分解，然后对分解后的系数进行阈值处理，最后重构得到去噪信号。对原始信号进行小波变换后，得到各尺度系数。随后确定阈值λ，若小波系数小于λ，则认为该系数主要由噪声引起，需要对该部分系数进行去除。若小波系数大于λ，则认为该系数主要是由信号引起，对该部分系数加以保留。对处理后的小波系数进行小波反变换，即可得到滤波之后的信号。

常见的阈值函数有：硬阈值函数(小波系数的绝对值低于阈值的置零，高于的保留不变)；软阈值函数(小波系数的绝对值低于阈值的置零，高于的系数shrinkage处理)。本文采用软阈值函数进行去噪处理。软阈值函数公式为：

(5)

式中：w表示小波系数，T为给定阈值，sign(*)符号函数。

1.3 小波变换滤波效果评价

本文采用求取均方差与相似度的方法对地震记录不同小波基的滤波效果进行评价。

均方差σ是总体各单位标准值与其平均数离差平方的算术平均数的平方根。它反映组内个体间的离散程度。定义式如下：

(6)

由定义可知，滤波后信号与原始地震记录之间的均方差越小，二者相似程度越高，滤波结果越接近原始地震记录。相似度ρ的定义式如下：

(7)

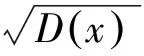
2 一维信号的滤波结果分析

以鄂尔多斯盆地北部地震资料为例，该区主要目的层气藏多以岩性控制为主，少部分为构造—岩性型油气藏。原始地震剖面如图1所示，在主要目的层(1 700～1 900ms)山西组、太原组、石盒子组，主要发育有T9b+c、T9d、T9e、T9f四组反射波，形成一个强振幅、连续性好的密集反射段。测线西部局部地段反射杂乱、连续性差，出现反射同相轴的合并、分叉等现象。提取该地震剖面中的第308道地震记录，对其进行小波分析。小波变换的尺度越大，越容易获取信号的低频特征；反之，尺度越小，获取的主要是信号的高频特性。地震信号的小波变换是一种先验的时频分析方法，其小波分析结果不仅取决于信号本身，而且也与所采用的分析小波有关。在进行地震信号的薄互层高分辨率分析时，恰当地选择小波函数是至关重要的。

在常用的小波基函数中，考虑正交性、双正交性、紧支撑等性质，选取Daubechies[13]、Coiflets、Symlets三种函数(缩写分别为db、coif、sym，表示形式为：dbN、coifN、symN；N为消失矩)。

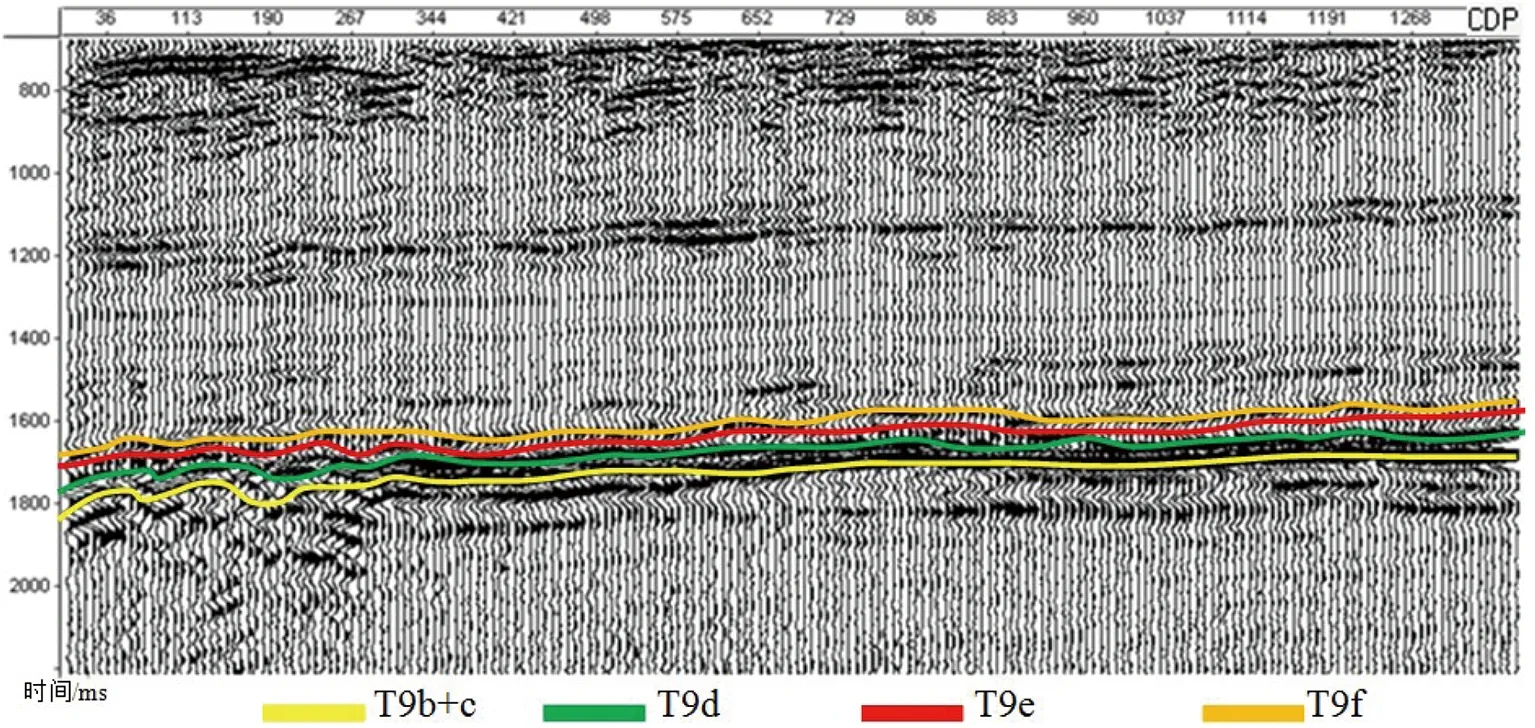
图1 待处理地震剖面Figure 1 Seismic section to be processed

首先选用db3小波，该小波系是一系列二进制小波的总称，是由法国学者Daubechies提出的，故称为db小波。Daubechies小波不仅是连续和正交的，而且是支集最小的，这种小波的滤波器个数少，在地震信号的分解和重构中计算量小。该小波没有明确的解析表达式，其有效支撑长度为2N，消失矩为N。实际地震信号中的噪音通常表现为高频成分，因此对信号进行二尺度一维分解，所得结果如图2所示。随后采用软阈值处理方法进行小波阈值滤波，其结果如图3所示。

然后采用sym2小波对信号进行分析。Symlets小波与dbN小波相比，在连续性、支集长度、滤波器长度等方面与dbN小波一致，但symN小波具有更好的对称性，即一定程度上能够减少对信号进行分析和重构时的相位失真。Symlets小波也是对一系列小波的总称，这类正交小波的支撑长度为2N-1，滤波器的长度为2N，消失矩为N，具有相似的对称性。此次采用尺度函数与db3相近的sym2小波对信号进行二尺度一维分解，进行软阈值滤波后，得到的结果如图4所示。

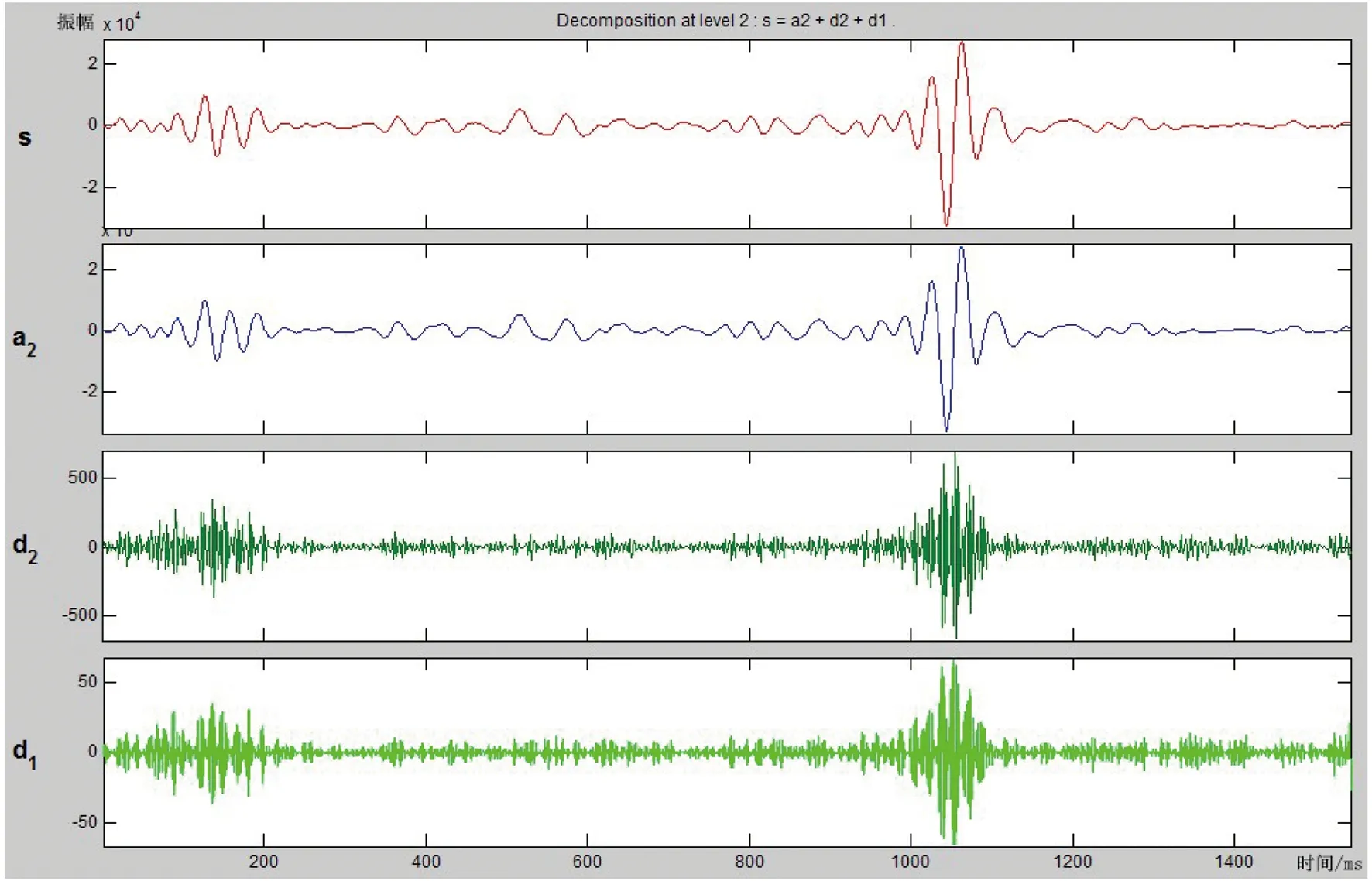
s：原始信号；a2：二阶低频分量；d1：一阶高频分量；d2：二阶高频分量图2 db3小波变换结果Figure 2 Transformed results of db3 wavelet

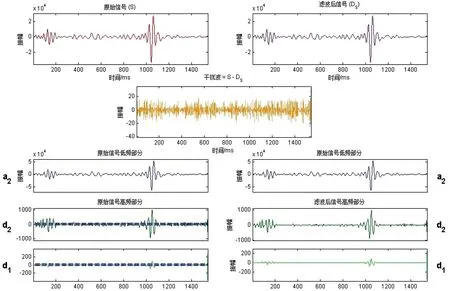
图3 db3小波阈值去噪结果Figure 3 Denoised results of db3 wavelet threshold

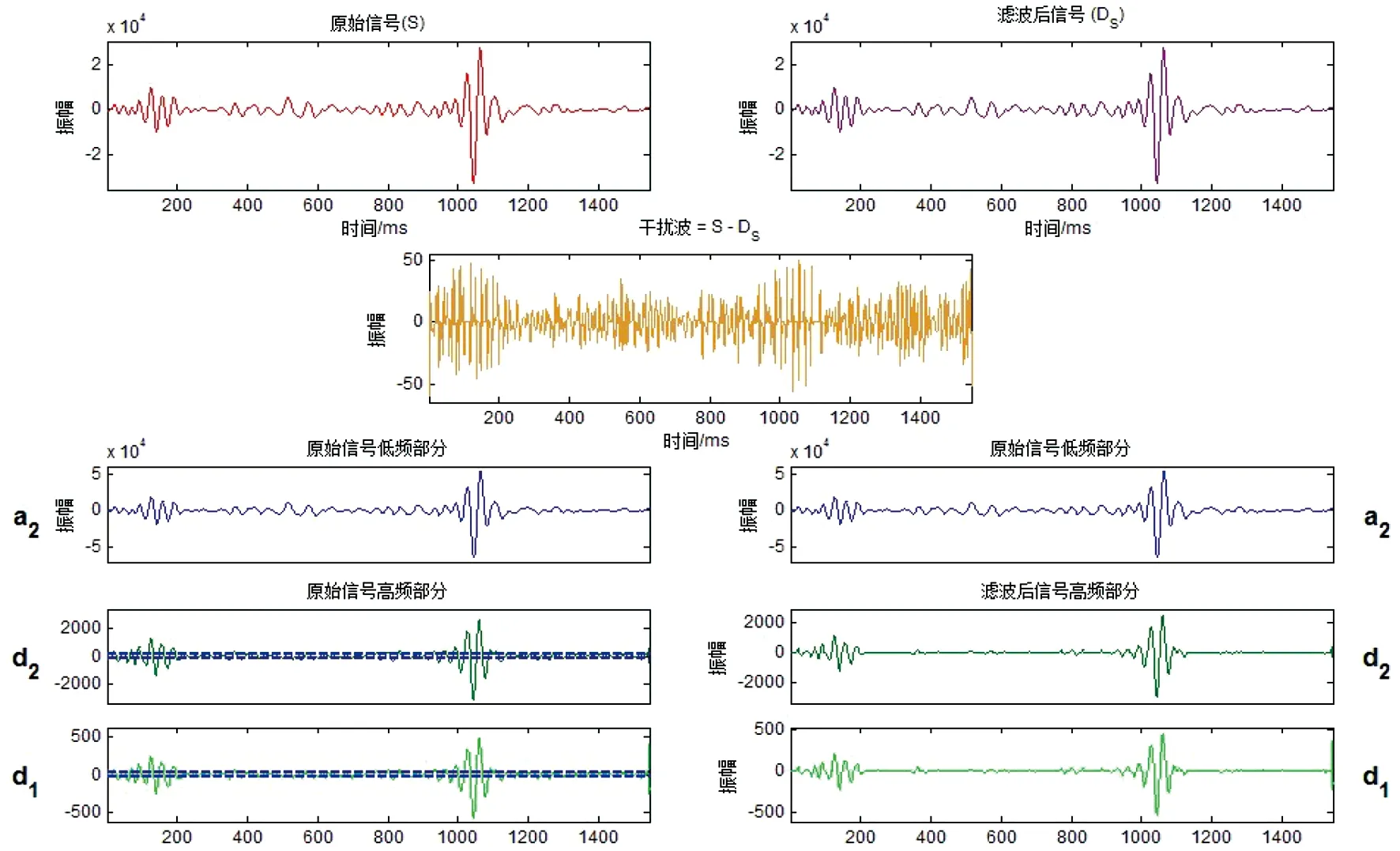
图4 sym2小波阈值去噪结果Figure 4 Denoised results of sym2 wavelet threshold

随后采用coif1小波对原始信号进行变换。Coiflet的小波函数的2N阶矩为零，具有比dbN更好的对称性。Coiflet小波系属于双正交的小波，该类小波的支撑长度为6N-1，滤波器的长度为6N，消失矩为2N，其对称性要好于db小波。选用尺度函数与db3小波接近的coif1小波对原始信号进行二尺度一维分解，进行软阈值滤波后所得结果如图5所示。

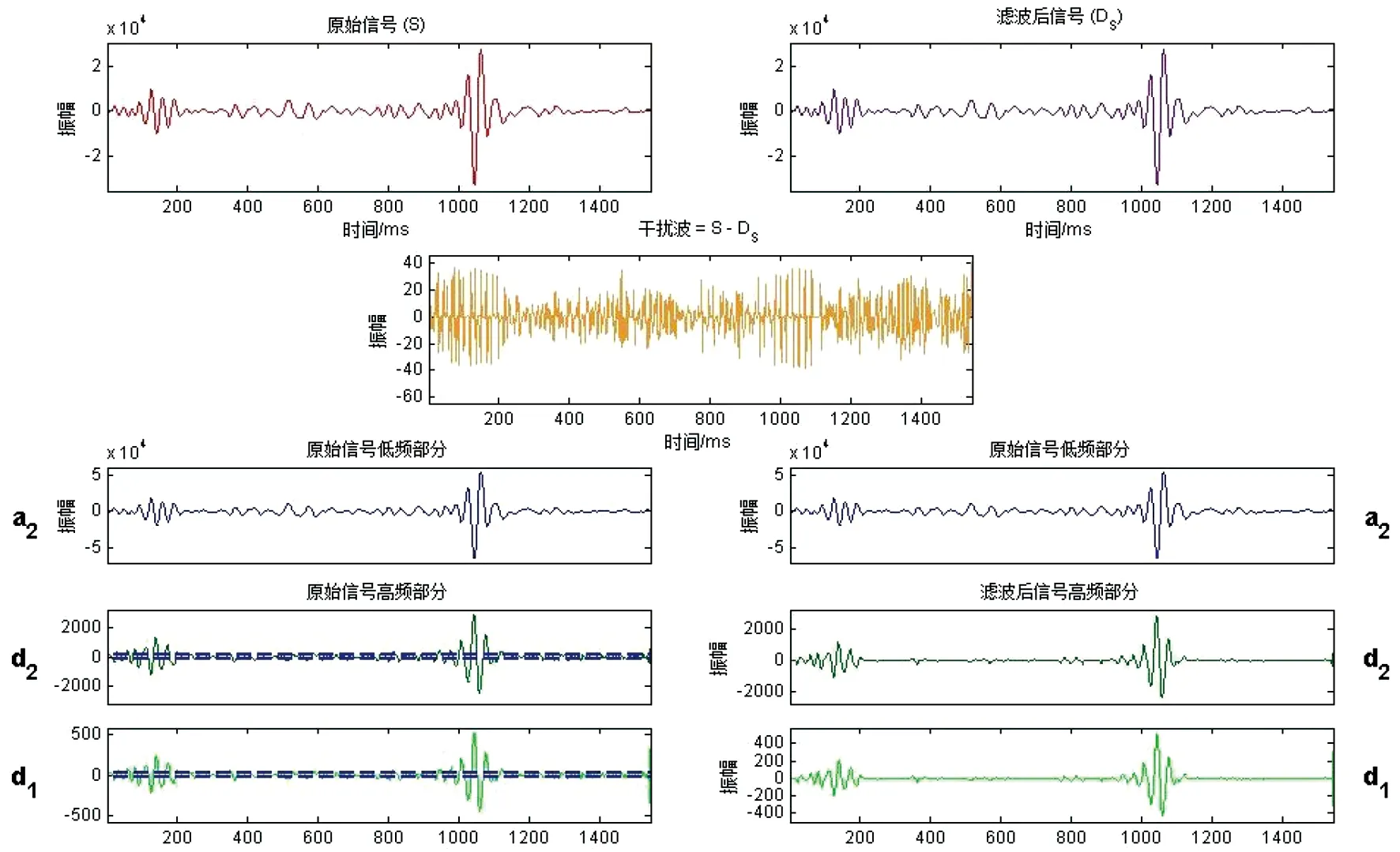
图5 coif1小波阈值去噪结果Figure 5 Denoised results of coif1 wavelet threshold

通过选用三种不同的小波基函数对第308道数据进行了阈值滤波后，采用求取滤波后信号与原始地震信号的均方差与相似度的方法进行比较，选取最优化的滤波结果。详情见表1。

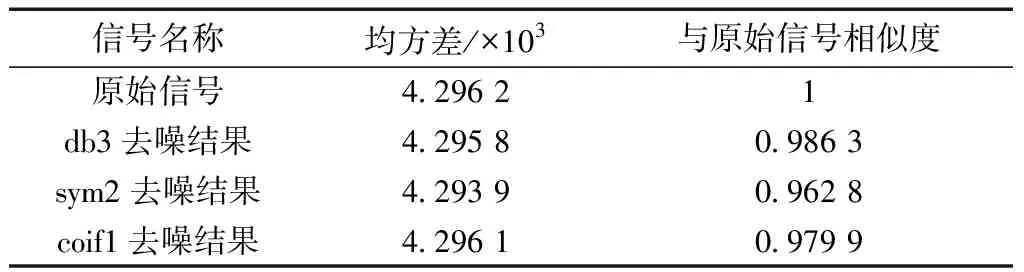
表1 滤波结果的均方差与相似度

由上表可知，从均方差来看，sym2去噪结果均方差最小，说明其对噪声消除效果最好，db3去噪结果次之，coif1去噪结果均方差最大；从相似度来看，db3去噪结果与原始信号的相似程度最高，coif1去噪结果与原始信号相似程度次之，而sym2去噪结果与原始信号相似程度最差。综合考虑来看，对该工区地震记录进行小波阈值滤波时选用db3小波基函数最为合适。

3 小波包对二维信号的滤波结果分析

经过上一节的讨论可以得出结论，选用db3小波基函数对该工区地震记录进行滤波处理效果最好，因此采用db3小波对二维地震剖面进行小波包滤波。

小波包分析是小波分析的延伸，该方法对信号的时频分析更为细致。其原理如下：小波分解实际是将信号分成高频与低频两个部分，筛选出高频部分之后对剩余的低频部分再一次做分解，再次筛选出高频与低频部分，直到达到规定的尺度。小波包分析与之不同之处在于，针对每一次筛选出来的高频部分继续做分解，也就是说对每一次分解得到的所有结果继续进行分解。由于小波变换不具备自适应的特征，所以高频成分中可能也包含有低频信息，因此采用小波包分析能够将高频成分中的低频信息也分解出来，其时频分析能力会得到进一步的提升。

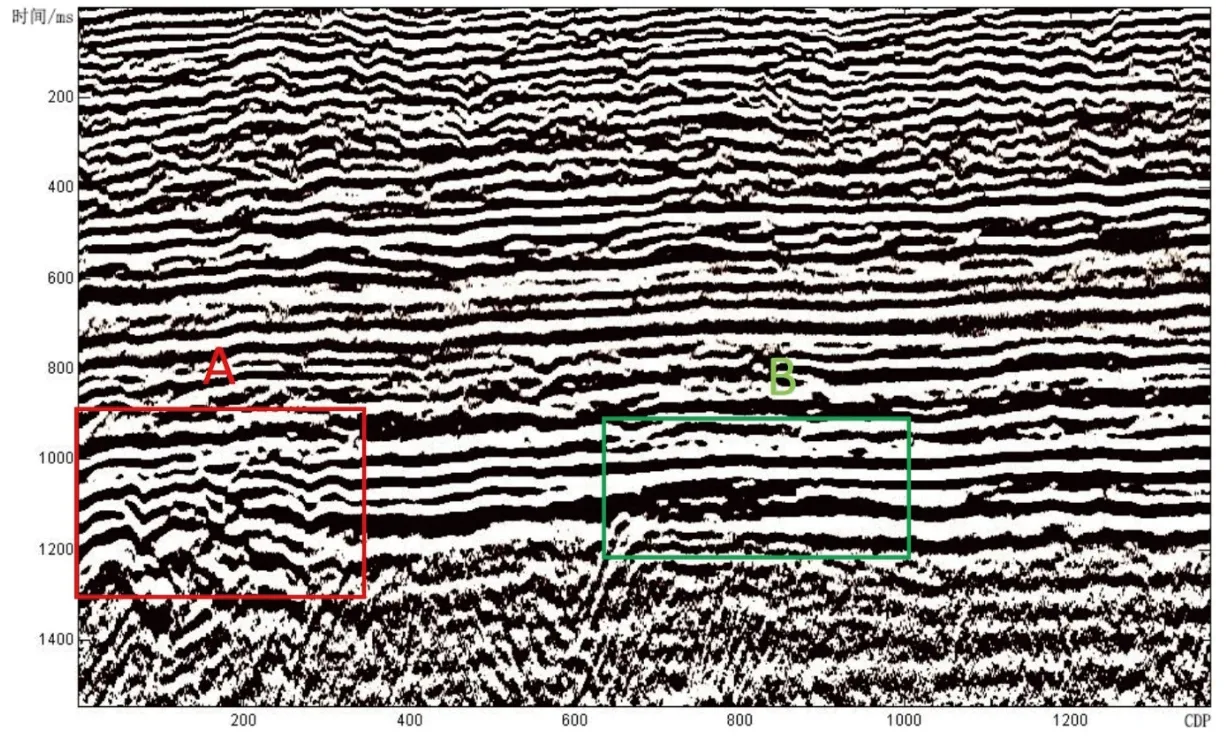
(a)原始信号

(b)滤波信号图6 二维地震数据的滤波效果对比Figure 6 Filtering effects comparison of 2D seismic data (left: original; right: denoised)

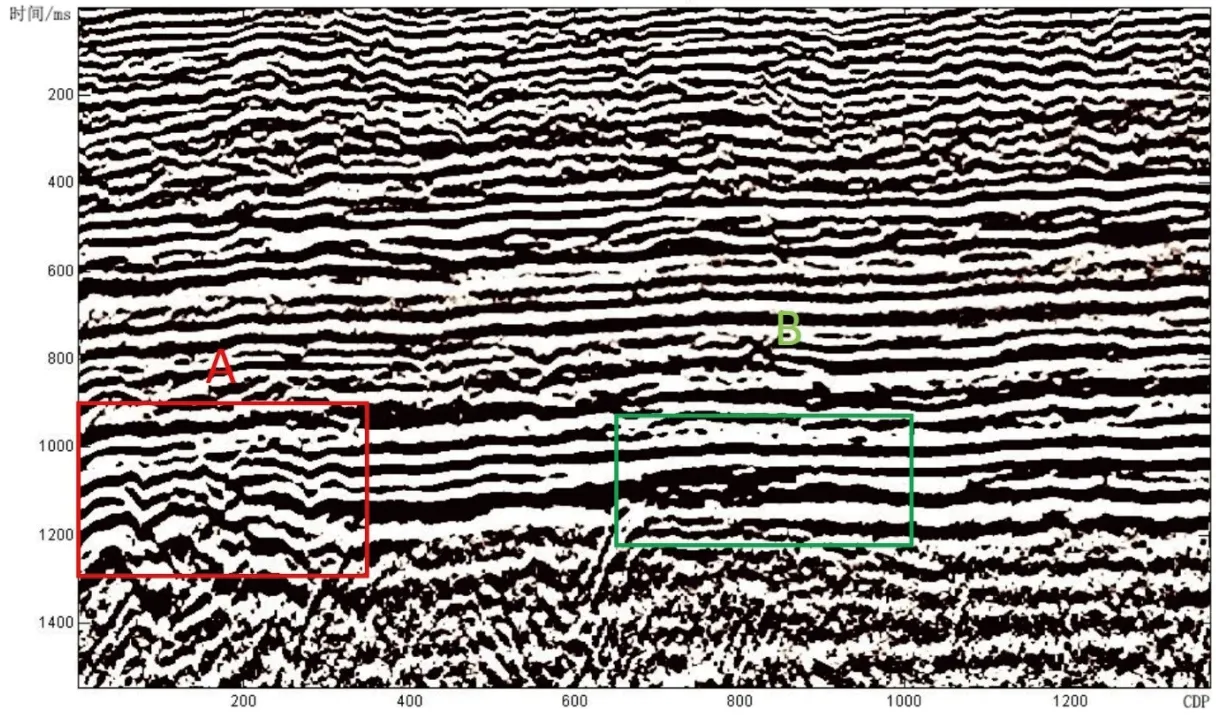
图7 A、B区域对比放大图Figure 7 Comparison of A and B regions enlarged images

对二维地震数据进行滤波处理后，选取地震剖面中的几处细节进行放大对比，对滤波效果进行验证，如图6、7所示。从图中可以看出，原始信号剖面图中存在许多“毛刺”现象，而进行小波阈值滤波之后，滤波后的图中高频干扰明显降低，同向轴的形态更为清晰圆滑。图7为滤波效果局部放大图，效果更佳明显。可见采用db3小波进行滤波之后，所得剖面中的随机噪音得到了很好的压制，有效信号更加突出，信噪比得到了提高。

4 结论

本文通过对实际工区资料进行小波变换滤波处理，并对结果进行分析总结后，可以得出一下几点结论。

①不同的小波基函数选取会对滤波效果产生影响，需要结合质特点和地震响应特征，多尝试几种不同的小波基函数，并从中找到效果最佳的小波基函数进行分析。

②针对该工区地震资料，db3小波阈值滤波效果最好。处理后的反射层特征变得更清晰，同相轴连续性增强，资料频带向高频方向拓宽，高频成分明显加强，低频部分有所保持；随机噪音得到了很好的压制，有效信号更加突出，信噪比得到了提高。

③小波包滤波能够有效降低地震剖面中的高频干扰，其结果可用于精细解译地震波信号，更好地服务于气田地震信号的解译工作。