Burgers-Huxley方程的两类精确解

夏鸿鸣，高忠社

（天水师范学院 数学与统计学院,甘肃 天水741001）

1 引 言

形如

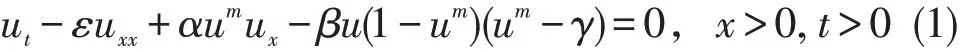
(其中ε,α,β,γ,m 为正常数)的方程称为Burgers-Huxley 方程，是由Satsuma 于1986 年首次提出的.[1]方程(1)是一类非线性反应扩散方程，它描述了对流效应和扩散传输之间的互动反应.此外，方程(1)还是一些著名的非线性方程的一般形式，例如，

当β=0，γ=0，ε=1时，方程(1)为Burgers方程

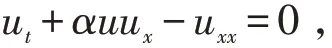
当m=1，α=0，β=1，γ=0，ε=1 时，方程(1)为Huxley方程

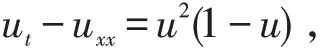
当m=1，α=0，β=1，ε=1 时，方程(1)为Fitzhugh-Nagumo方程

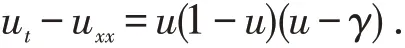
由于方程(1)的十分重要的理论和应用价值，受到了许多研究工作者的关注并得到了大量的研究成果，Khadija Gilani，S.C.Shiralashetti，Neeraj Kumar Tripathi求得了方程(1)的数值解，[2-4]邓习军研究了其行波解，[5]N.A.Kudryashov 研究了其精确解，[6]王勤龙等讨论了方程(1)的平衡点及分支类型.[7]

非线性偏微分方程因其更精确、更广泛地描述了众多自然现象而成为数学和物理研究的主流方向，但是其解析解法却是一个难点。近些年来，该问题得到了很大的突破，人们用反散射方法、[8]Backlund 变换、[9]双线性方法，[10]齐次平衡法、[11]Riccati 方程映射法[12]和分离变量法[13]等多种方法得到了大量非线性偏微分方程的精确解、行波解、孤立子解，试探函数法也是其中较为有效的方法之一，学者们使用试探函数法求得了一些非线性偏微分方程的精确解，[14-17]高忠社等人求出了特殊形式的Burgers-Huxley 方程的奇异行波解和扭状孤波解，[18]本文尝试使用试探函数方法对一般情形的Burgers-Huxley 方程(1)展开讨论.

2 方法简介

文献[15]利用Cole-Hopf 变换，通过选择适当的试探函数，将非线性偏微分方程化为一个代数方程组，再利用待定系数法确定相应的常数，可得非线性偏微分方程的解析解.具体过程如下：

对于非线性偏微分方程

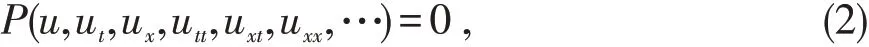
引入试探函数如下:

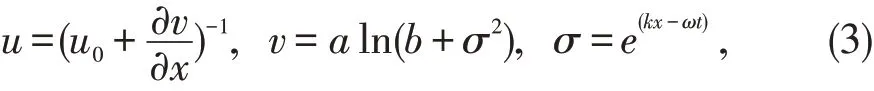
其中u0,a,b,k,ω 为待定常数，则有

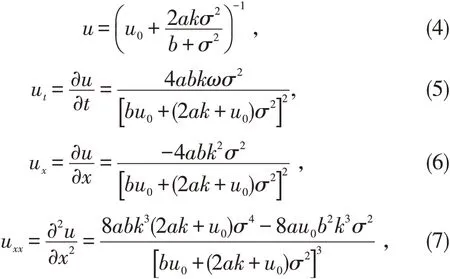
将(3)～(7)代入方程(2)可得相应的代数方程组，将代数方程组的解回代到(3)，即可求得方程(2)的精确解.

3 非线性Burgers-Huxley方程的求解

考虑Burgers-Huxley方程

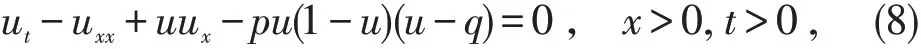
其中p,q 为常数.将(3)～(7)式代入方程(8)，得到如下的代数方程：

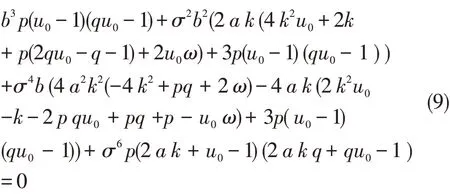
为使(9)式对任意的实数σ 都成立，需要如下代数方程组

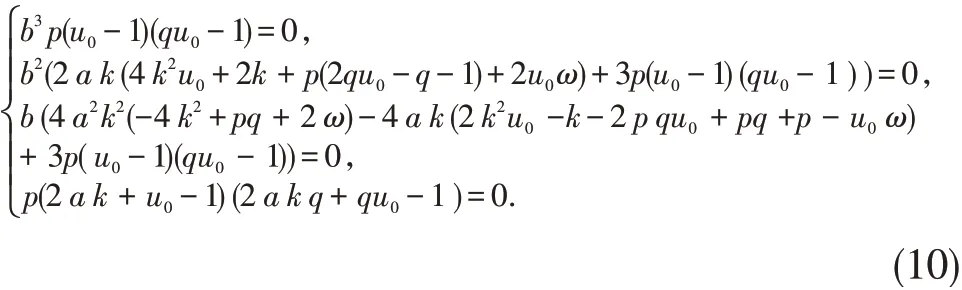
存在（其中b 为任意的常数）.求解(10)式,得方程组关于p,q 的解

同理，将(12)式中的u0和a 代入(3)式，可得

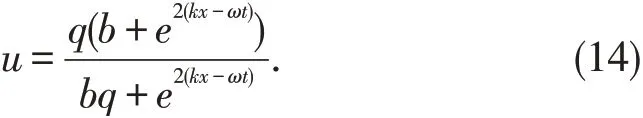
(13)和(14)式为方程(8)的行波解，对应于b 的不同取值，可以得到方程(7)的多个不同的特解.例如：

情形1令b=1，由(13)和(14)式，可得方程(8)的扭状孤波解

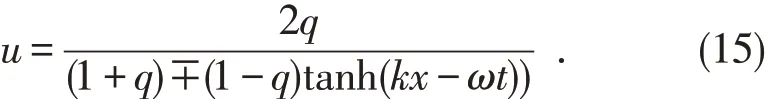
情形2令b=-1，由(13)和(14)式，可得方程(8)的奇异行波解

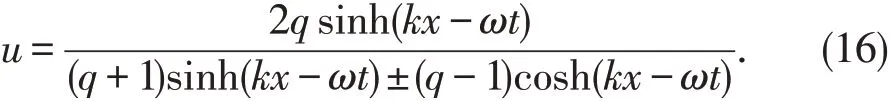
由于双曲函数和三角函数具有如下关系

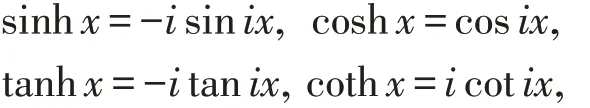
作变换k=ik,ω=iω，还可以进一步讨论(15)和(16)周期波解的相关性质，从略.

给予b 不同的值，所得方程(8)的解的结构和相关性质可以使用如上的方法进行讨论，本文不再赘述.