基于改进模拟退火算法的采煤机滚筒调高优化研究

赵有生，贾 文，王强喜，盛长斌，闫孝姮

(1.山西焦煤集团投资有限公司，山西 太原 030024；2.山西焦煤集团岚县正利煤业有限公司，山西 吕梁 035200；3.辽宁工程技术大学 电气与控制工程学院，辽宁 葫芦岛 125105)

目前采煤机智能化自动割煤已经成为综采工作面的主要发展方向和发展趋势，实现滚筒的快速和稳定的调高是实现采煤机智能化、无人化割煤的关键技术[1-3]。针对采煤机滚筒自适应调高，陈浩峰[4]等建立了滚筒调高关键元件阀控缸的数学模型，为以后调高控制策略的发展提供了研究基础。张修荣[5]从电液比例控制系统出发建立了调高系统的传递函数，进一步使用了PID控制器对调高系统控制，这种方式虽然比开环控制更加稳定，但是没有提及寻找最优的PID参数的方式。针对传统闭环控制具有的不灵活、适应性差的缺点，赵丽娟[6]，等建立了滚筒调高的传递函数，进一步提出了基于模糊PID的采煤机调高控制策略，通过仿真证明了这种控制策略与传统PID相比具有较好的平稳性和快速性。高永新[7]等利用MATLAB/simlink中的工具箱构建了采煤机调高控制系统的仿真模型，通过输入不同的信号证明了模糊自适应PID比传统PID 具有位置跟踪性能好的优点。冯凯[8]等，使用以遗传算法寻优后的PID参数构建了采煤机调高系统的PID控制器，结果表明使用这种优化后的参数的PID控制器，比传统控制器具有响应速度快，跟踪平稳性好的优点。但是，上述控制策略具有一定的局限性，模糊PID中的模糊控制经验复杂，隶属函数关联性较高，且模糊控制器的设计依赖于现场的专家经验。遗传算法的局部搜索能力较弱且计算量大，往往需要多次寻优才可以得到局部最优的值。因此本文提出一种基于改进的模拟退火算法的采煤机滚筒调高控制策略，不仅具有传统模拟退火算法的优秀的局部搜索能力，而且通过回火行为增强了算法的全局搜索能力，精准确定采煤机滚筒调高的PID参数，利于煤炭生产。

1 改进的模拟退火算法

1.1 传统模拟退火的原理

模拟退火算法求解思想和过程与热力学中固体熔融再凝固这一退火过程相类似，在工程中运用模拟退火算法寻优的基本原理是，将实际问题中要优化的目标函数作为模拟退火算法中的目标函数，将目标函数的解空间对应状态空间，按照状态产生函数随机的产生解，根据接受概率选择是否接受当前解为新解，逐步寻优的过程。

1.2 传统模拟退火算法寻优的过程

1)初始化：给定初始温度Tk(k=0)，随机初始化解x0，退火系数λ，内外部中止条件，以及能量函数。

2)在当前温度下，在当前最优解xk的邻域内根据状态产生函数随机的产生新解x’；根据目标函数的函数值来判断新解x’是否直接满足优化条件，若是则用新解x’来替换当前解xk。若不是直接满足则计算当前解是否在Metropolis准则决定的接受概率下，若在接受概率下，依然用新解x’来替换当前解xk。否则，舍弃掉新解。

3)根据内部循环中止原则判断是否应该中止内部循环，常用的内部循环准则是：判断在温度T下是否达到了规定的迭代次数即链长L，或者满足平衡条件。若满足则转到步骤(4)，若不满足则跳转到步骤(2)。

4)退温过程：令k=k+1，Tk+1=λTk。

5)判断是否满足中止条件，若满足则停止并寻优输出寻优完成的KP、KI、KD，若不满足则执行步骤(2)。

ITAE是常用的评价系统性能的指标，改变KP、KI、KD三个参数的值直接影响的是系统的性能，所以可以采用ITAE作为模拟退火算法的目标函数。其数学表达式为式(1)。可以看出ITAE的值越小说明选取的KP、KI、KD的值越合适。

1.3 模拟退火算法的改进

1)针对传统模拟退火算法会产生重复的解，在第(2)步引入禁忌搜索(TS)的思想。即构建一个长度为L的禁忌表将每次产生的优秀的采煤机调高参数按队列加入禁忌表中，若后面产生的采煤机调高参数在禁忌表中则返回重新生成，这样可以有效避免采煤机调高参数的重复生成，加强了全局搜索能力。

2)针对模拟退火算法在温度较低时难以跳出局部搜索的陷阱，在第(4)步中引入回火升温的过程，即当温度较低时适当的升高系统温度，有利于算法跳出局部搜索的陷阱，得到最优采煤机调高参数。

3)针对模拟退火算法的效率问题，在第(5)步中引入一种新的中止寻优的方法，即当目标函数的值已经连续λ次不发生较大的变化则可以认为寻优已经完成，采煤机调高参数已经得到。

2 采煤机调高系统的传递函数

采煤机滚筒调高系统，主要由摇臂机构、截割滚筒、阀控缸、反馈机构和液压控制回路来组成。采煤机调高系统实际上是一个电液比例控制系统，根据文献[5]，若忽略活塞运动过程中的黏性阻尼系数和外部干扰，可以得到采煤机调高系统的传递函数为：

式中，A1和A2分别为调高油缸内部活塞左右两腔有效面积，m2；Kq、Kf分别为反馈系数和等效系数；ωh和ξh系统阻尼比和固有频率系数。本文选取的采煤机的参数如下：2A1-A2=15×10-3/m2、ωh=163/rad·s-1、Kq=2/m2·s-1、Kf=1.5。带入式(2)可得采煤机调高系统的传函为：

3 仿真与验证

3.1 改进模拟退火算法的验证

图1 传统模拟退火算法各参数值随着迭代次数的变化

使用MATLAB分别编写传统模拟退火寻优算法和改进后模拟退火算法的程序，给定相同的初始参数(包括：初始温度T0=150，Metropolis链长L为200，降温系数γ=0.95，中止温度Te=1。)同时设置改进的模拟退火特有的参数如下：(回火系数λ=0.5，温度降低φ=30次解不变就中止寻优)。针对前文提出的采煤机调高系统的传函，编写相同的ITAE计算函数，根据系统整定的经验可以选取KP、KI、KD的取值范围分别是[0，90]，[0，20]，[0，0.15]。传统模拟退火算法和改进的模拟退火算法在寻优过程中KP、KI、KD最优解和ITAE的最小值随着迭代次数的变化过程分别如图1中的(a)、(b)、(c)、(d)、和图2中的(a)、(b)、(c)、(d)所示。经过对比可以看出虽然改进前后的算法都能够实现对KP、KI、KD的参数的寻优，但是改进后的模拟退火算法寻优得到的参数能够使的ITAE的值达到最小为0.02，而传统模拟退火算法寻优得到的参数值仅能够使ITAE的值达到0.08。这表明传统模拟退火算法陷入了局部寻优，同时也说明前文提到的针对模拟退火算法的改进措施能够使模拟退火算法有效的避免陷入局部寻优，得到全局最优解。

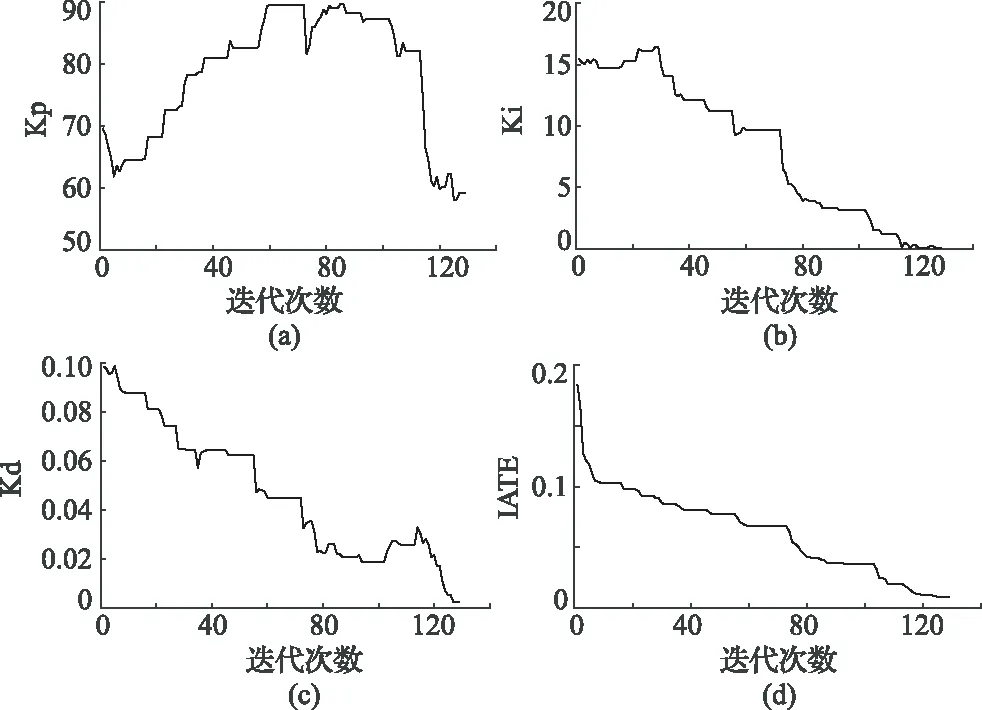
图2 改进后模拟退火算法各参数值随着迭代次数的变化

3.2 调高系统的仿真验证

由于任何优化算法都是理论上可以达到最优，所以为了避免误差，在进行多次仿真后取平均值得到最优值为KP=59，KI=0.1，KD=0.05。使用优化后的参数结合simulink中的仿真工具箱构建系统的仿真框图。仿真框图如图3所示。

图3 系统仿真框图

在第6s处给定幅值为1持续1s的扰动来验证其鲁棒性，其输出曲线如图4所示，从图4中能够看出，系统受到扰动后用了0.1s的时间恢复到稳定水平，表明系统对扰动有着较好的抗性，鲁棒性强。同时可以看到系统还具有较小抖震，表明系统具有良好的稳态特性。

图4 扰动仿真结果图

分别给系统输入幅值为1、周期为2、占空比为50%的方波信号和幅值为1、角速度为10πrad/s、的正弦信号来验证系统的信号跟踪特性，设置仿真时间10s和5s。仿真结果分别如图5、图6所示，从图中可以看出系统能够较好的跟踪不同的输入信号，表明系统有较好的跟踪特性。

图5 方波信号的跟踪仿真

图6 正弦信号的跟踪仿真

4 结 论

1)根据模拟退火算法理论前提，在传统的模拟退火算法的基础上引入了禁忌搜索、回火退火的思想。以采煤机调高系统的ITAE指标作为目标函数，结合MATLAB程序寻优计算了采煤机滚筒调高系统PID控制器的参数。

2)以采煤机调高系统的传函为基础，构建了采煤机滚筒调高系统的仿真模型，研究并分析了采煤机滚筒调高系统的跟踪特性和鲁棒性。通过对不同信号的跟踪，仿真结果表明设计的控制器稳定有效。为采煤机滚筒调高实现准确跟踪目标路径提供了一种有效途径。