一种新颖的微带六端口电路器件分析方法

于正永，徐 彤，董 进，唐万春

(1.淮安信息职业技术学院 计算机与通信工程学院，江苏 淮安 223003；2.南京师范大学 物理科学与技术学院，江苏 南京 210023)

0 引言

利用六端口电路器件可以精确测量电路反射系数的相位这一特性[1-2]，其被广泛应用于阵列天线相位校准[3]，也被应用于微波集成电路系统中接收机前端的设计[4-5]，越来越受到国内外研究人员的关注，因此较为快速、准确地分析六端口电路器件的特性十分重要。许多学者针对高性能的六端口电路器件进行了研究，文献[6]运用三维电磁仿真软件HFSS设计了带宽为2.3～11.5 GHz的宽带六端口结电路，文献[7]提出了一种基于并联枝节蜿蜒线的小型化微波六端口结，具有与传统结构相近的频率响应特性。作者曹煜针对微波通信系统中六端口技术进行了深入研究，设计了多种高性能的六端口电路器件[8]。目前对六端口电路器件的特性分析主要通过测试仪器和微波仿真软件提取[9]，这些方法对硬件设施的依靠性很强。本文结合传统的连接散射矩阵法[10-11]和微带线不连续性等效电路模型及理论[12-13]，考虑不连续性结构引入的传输损耗，进而准确分析了六端口电路器件散射参数，并与IE3D软件[14]仿真结果进行对比验证。

1 连接散射矩阵法的基本原理

多端口网络拓扑如图1所示，它是由p个任意端口网络互联而成的一个n端口网络，其中各个网络的散射矩阵是已知的，并且认为任一个连接都不改变各个网络的矩阵参量，分析的任务在于求出相连接后的总网络的散射矩阵。此处需要重申一下，分析是在2个互联的端口传输线特性阻抗相同的条件下进行的。当级联端口传输线的特性阻抗不相同时，只需把连接接头也作为一个级联于其中的二端口网络处理。

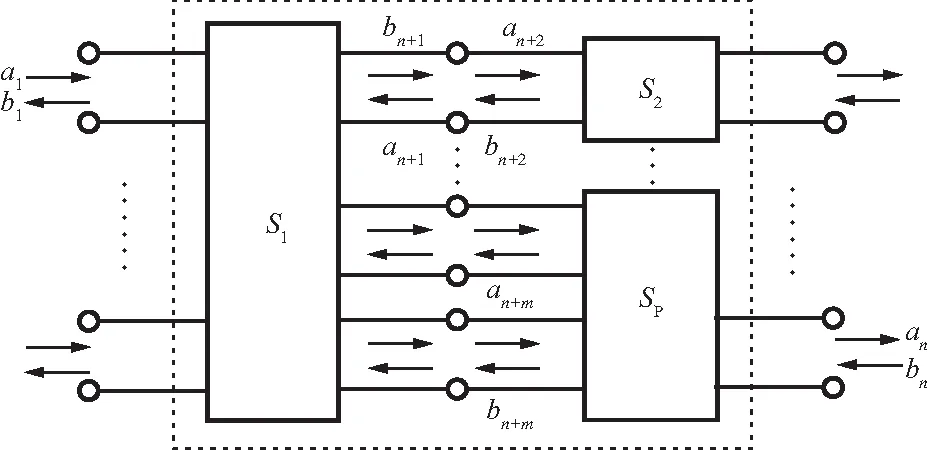
图1 多端口网络拓扑

假设各单个网络端口数目的总和为(n+m)，其中端口1～n是不连接端口，它们构成待求n端口网络的端口，端口(n+1)～(n+m)是一对一相互级联连接的互联端口。连接方式是端口(n+1)和(n+2)相级联，端口(n+3)和(n+4)相级联，……，端口(n+m-1)和(n+m)相级联。显然m必须为偶数。为求出连接后总网络的散射矩阵，首先假定所有互联端口全部断开，组成一个(n+m)端口网络，此(n+m)端口网络的散射矩阵称为联合散射矩阵，通常阶数较高，但往往是稀疏矩阵，以Sc表示，其关系如下：

(1)

缩写形式为：

b=Sca。

(2)

由于网络尚未连接，各单个网络互为独立，因此有许多端口互不相关。在联合散射矩阵Sc中，除包含所有各单个网络的散射参量外，其余元素均为零。将联合散射矩阵Sc写成分块矩阵的形式为：

(3)

式中，

然后将所有互联端口连接，根据微波网络在同一参考面的连接特性[15]，可获得级联端口处的连接条件：

bn+1=an+2bn+2=an+1
bn+3=an+4bn+4=an+3
………… …………
bn+m-1=an+mbn+m=an+m-1。

(4)

用矩阵形式表示为：

(5)

其缩写形式为：

aⅡ=εbⅡ，

(6)

式中，aⅡ和bⅡ为式(5)的列矩阵，而ε称为连接矩阵。把式(3)按分块矩阵展开，并将式(6)代入可得：

(7)

由式(7)中第2个矩阵方程进一步获得：

bⅡ=(E-SⅡⅡε)-1SⅡⅠaⅠ，

(8)

式中，E为单位矩阵。再将式(8)代入式(7)中第1个矩阵方程中，可得：

bⅠ=SⅠⅠ+SⅠⅡε(E-SⅡⅡε)-1SⅡⅠaⅠ，

(9)

其缩写形式为：

bⅠ=SaⅠ，

(10)

式中，

S=SⅠⅠ+SⅠⅡε(E-SⅡⅡε)-1SⅡⅠ。

(11)

式(11)为连接后总网络的散射矩阵。由于连接矩阵ε是一个实数正交矩阵，具有性质εε=1，或ε=ε-1，则式(11)可写成：

S=SⅠⅠ+SⅠⅡ(ε-SⅡⅡ)-1SⅡⅠ。

(12)

在应用式(12)前，应该先编排好多端口网络各个端口的序号，把一对一级联连接的互联端口依次编排在非互联端口后面，不可混乱，这是非常关键的步骤。

2 计算步骤及方法

根据推导的总网络散射参数计算公式和已有的微带线不连续性等效电路模型，使用Matlab语言[16]进行算法编程，计算六端口电路器件的散射特性，计算方法如下：

① 对微带六端口电路器件进行单元子网划分，很显然划分为功分器、分支耦合器、直角拐角和传输线等子网形式，然后对每个单元子网的端口进行编号。

② 编写各单元子网S参数提取的算法程序。各个单元子网的散射参数可运用文献[12-13]中的不连续性等效电路模型及理论编写程序进行提取。

③ 微带六端口电路器件的散射参数计算程序编写。根据连接—散射矩阵法，首先需要构造联合散射矩阵。该矩阵是按照非互联端口和互联端口顺序排列的，但是在导入子网S参数时，是按照网络顺序导入的。若将子网S参数一个个提取、全部重新排列，较为繁琐且容易出错。在研究了端口排列顺序的变换规律以后，发现：列向量a，b中的元素按照同样的规律同时排列以后，只要对S矩阵的行按同样的顺序进行调整，再对列也进行如上的变化即可。这样只需将导入的各子网矩阵按网络编号以对角线方式构造成原始的全矩阵：

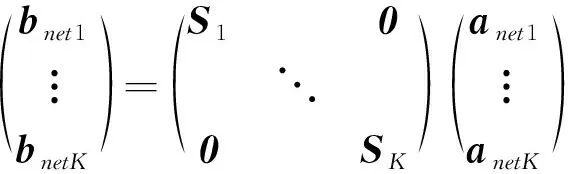
(13)

式中，bnetK，anetK分别表示第K个子网的散射波和入射波向量；SK表示第K个子网的散射矩阵。

在输入互联关系以后，按照重排的端口顺序，进行上述变化，便可以得到计算所需的联合散射矩阵式(1)。此后，按非互联和互联端口对联合散射矩阵分块，由理论推导的公式编程计算得到微带六端口电路器件的散射参数。

3 微带六端口电路器件设计及分析

微带六端口电路器件结构如图2所示。对称部分的功分器(右边)和耦合器(下方)结构未具体画出，用方框示意，结构参数与对称部分相同。基本参数：εr=2.55，h=0.5 mm，不连续性传输线长度Δz=2h=1 mm，W1=1.44 mm，W2=0.4 mm，W3=0.8 mm，W4=2.4 mm。

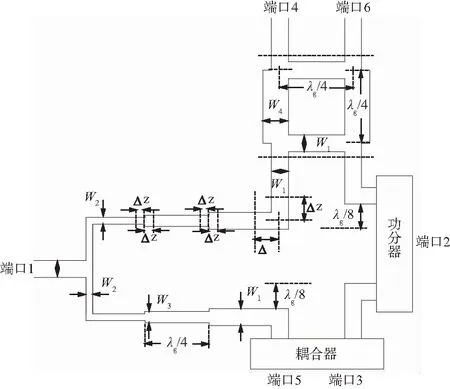
图2 微带六端口电路器件结构

将图2所示的微带六端口电路器件划分为16个单元子网，单元子网编号和端口编号如图3所示。其中，单元子网1，2为功分器；单元子网3，4为分支耦合器；单元子网5，6，7，8为直角拐角；单元子网9，10，11，12，13，14，15，16为普通传输线，尺寸有所变化，尤其要注意传输线单元子网12，9分别要比传输线单元子网10短，长度为λg/8，这将影响到端口3与端口5、端口4与端口6输出信号之间的相位关系。其中直角拐角、功分器以及分支耦合器单元子网散射参数可以通过文献[12-13]中微带线不连续性等效电路模型计算获得，普通传输线可以直接使用传输线散射参数公式计算获得[17]。在运用本文方法进行六端口电路器件散射参数计算时，需要对图2中所有端口按照单元子网顺序标号，然后再按照非互联和互联端口进行顺序排列，共划分为38个端口，其中非互联端口有1，4，32，34，36，38，其余32个(16对)端口为互联端口，具体对应关系如图3所示。

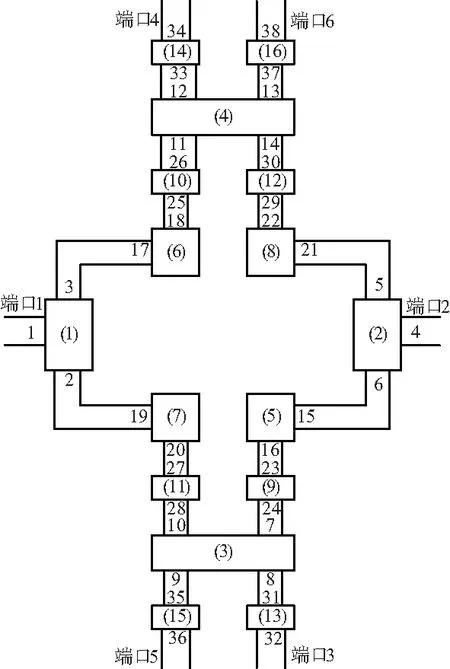
图3 微带六端口电路器件单元子网划分及端口编号

运用本文方法和IE3D软件仿真2种方法计算所得的S11和S52幅度对比曲线，如图4(a)和图4(b)所示。

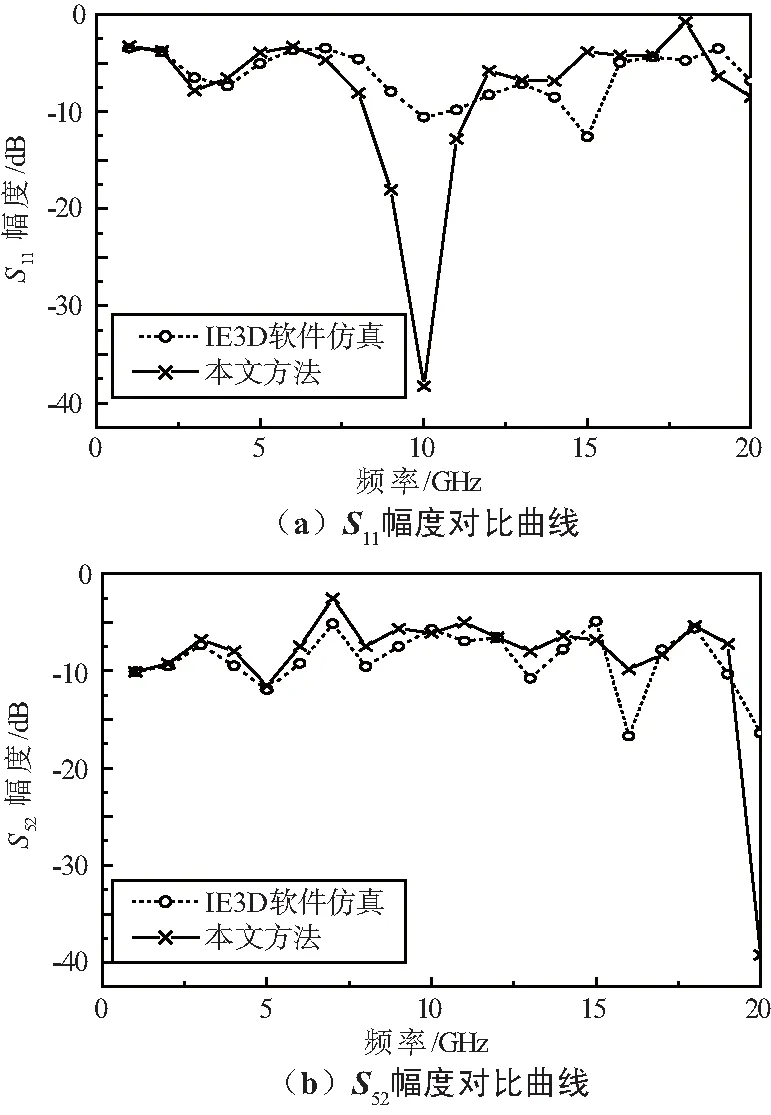
图4 S11和S52幅度对比曲线

从图4中可以发现，2种方法计算结果曲线的变化趋势是一致的，本文方法计算结果和IE3D软件仿真结果吻合较好，由于其单元子网散射参数已存在误差，因此这里的偏差量对于工程应用来说是可以接受的。S31相位和S51相位的IE3D仿真结果和本文方法计算结果如图5(a)和图5(b)所示，设计时耦合器输入口和隔离口的传输线长度相差λg/8，所以在中心频率附近应有90°的相位差。从图5中可以很明显看出，本文方法计算结果和仿真结果都较好地验证了这一点。S41相位和S61相位的IE3D仿真结果和本文方法计算结果如图6所示，可以看出均满足六端口电路器件的相位要求。

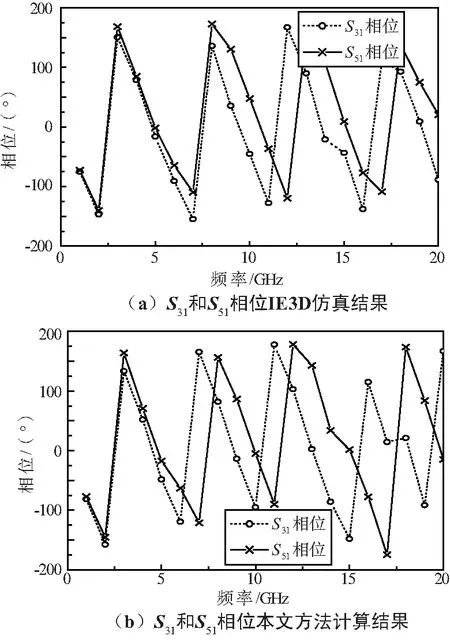
图5 S31和S51相位计算结果

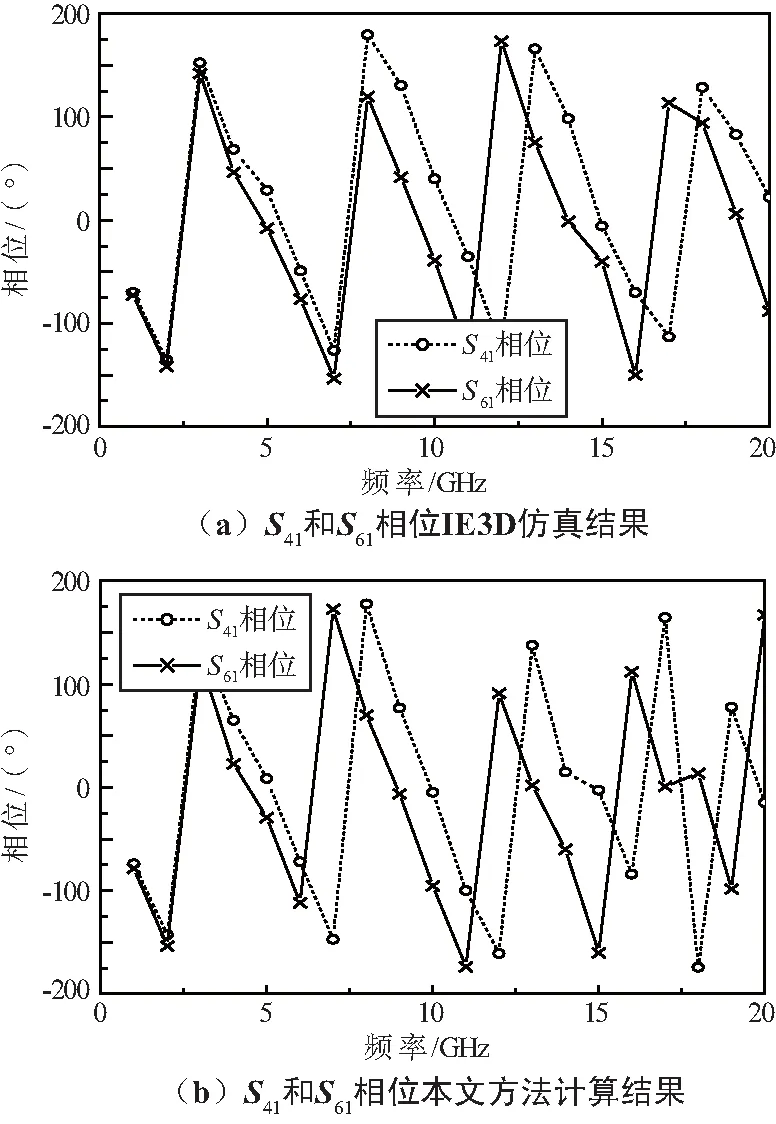
图6 S41和S61相位计算结果

运用本文方法和IE3D软件仿真2种方法计算所得的8～12 GHz范围内S31和S51相位的对比曲线如图7所示，运用本文方法和IE3D软件仿真2种方法计算所得的8～12 GHz范围内S41和S61相位的对比曲线如图8所示，对比结果均进一步验证了90°相位差要求，同时也可以发现，本文方法所得的曲线斜率较大，且相位变化较快。

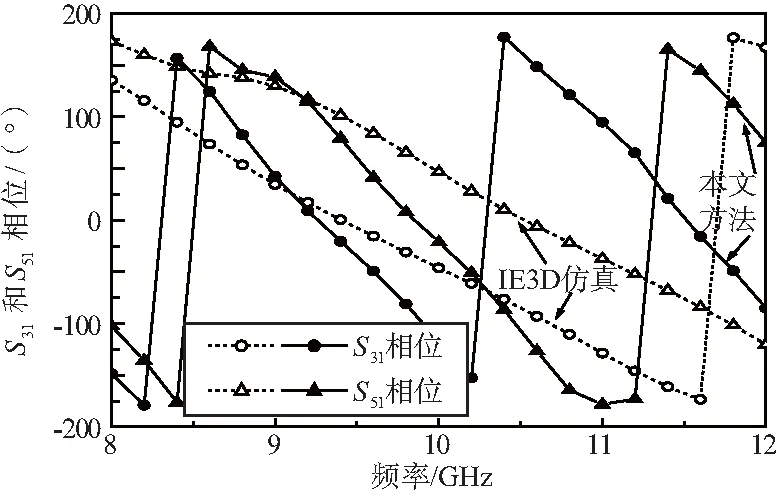
图7 8～12 GHz范围内S31和S51相位对比曲线

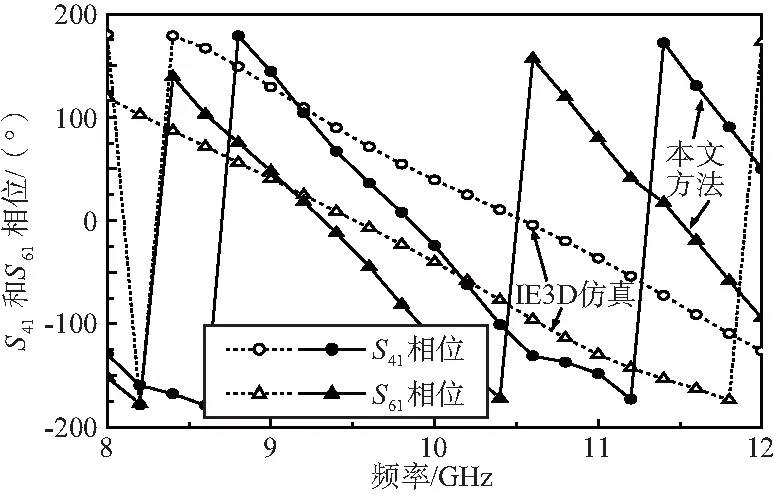
图8 8～12 GHz范围内S41和S61相位对比曲线

4 结束语

运用传统的连接散射矩阵法和微带线不连续性等效电路模型及理论，分析并提取了微带六端口电路器件的散射参数。引入已有的微带线不连续性等效电路模型，解决了传统的连接散射矩阵法存在的局限性，本文方法计算结果与IE3D软件仿真结果一致性较好，平均误差小于2%，为微波集成电路的设计及应用提供了参考。