基于贪婪策略的遗传算法求解多星观测任务优化
2019-12-24雷明佳陈韬亦陈金勇冯小恩
刘 翔,雷明佳,陈韬亦,陈金勇,冯小恩
(1.中国电子科技集团公司 航天信息应用技术重点实验室,河北 石家庄 050081;2.哈尔滨工业大学 深空探测基础研究中心,黑龙江 哈尔滨 150080)
0 引言
多星观测任务优化是指在一定的优化目标指导下,对多个观测任务进行排程,进一步确定需要择优执行哪些任务,以及执行这些任务的卫星和时间窗口。随着近几十年航天事业的不断进步与发展,我国在轨运行和规划研制的观测卫星的数量和种类均在不断增多,与此同时也对观测卫星的任务规划提出了十分严峻的考验[1-3],因此研究高效、准确且有工程实践价值的卫星观测任务优化算法具有重要意义。
目前国内外已有大量针对不考虑数据下传的卫星观测任务优化问题的研究。Mohamed等[4]将spot5卫星的日调度问题直接转化成对benchmark问题,并采用遗传算法求解,文献[5-7]则进一步提出了改进算法,在一定程度上提高了算法的求解精度和求解速度。Zhaojun Zhang[8]在研究多星控制资源规划问题时提出一种复杂的独立集合模型,并建立了基于蚁群优化的规划算法。陈英武等[9]建立了多星任务规划模型,并设计了基于动态参数决策模型的演化学习型蚁群算法。文献[10-11]则对分布式卫星系统采用粒子群优化算法求解其多任务数传调度问题。Wang和Qiu等[12]首次建立了对分布式成像卫星应急任务的新型多目标动态调度模型,并将任务进行合并。文献[13-15]分析了卫星运行及观测活动过程中的部分约束条件,并建立了相应的数学模型。
以上文献针对所研究问题提出的求解方法虽在一定程度上取得了较好的效果,但普遍存在着约束不全面或计算耗时长的问题,本文针对多星观测任务的优化问题,在基于对各种复杂约束分析的基础上,提出了一种基于贪婪策略的遗传算法,通过将贪婪算法的核心思想与遗传算法有机结合,在保证算法求解精度的同时提高算法的收敛速度。
1 多星观测任务规划问题描述
1.1 卫星观测任务模型
多星观测任务优化的过程实际就是对卫星观测任务加以选择的过程,而卫星的观测任务模型是根据工程实践需要以及用户需求建立的,可用如下模型描述:
tasknq
{
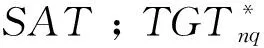
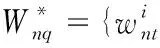
Datanq;xnq
}
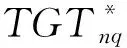
1.2 观测任务规划模型
信息实时获取条件下的多星观测任务规划(Multi-Satellite Observation Task Planning,MuSOTP),就是假设在给定规划时段内的任务与观测资源不变且星际链路稳定的条件下,多颗能力异构的对地观测卫星完成任务分配。将多星观测任务规划问题表述为:
MuSOTP={SAT,TGT,W,TASK,RES;STATE},
其中,W表示所有可见窗口集合;TASK表示卫星观测任务集合,TASK={task11,…,task1r1;…;taskN1,…,taskNrN};RES表示约束条件集合;STATE表示所有观测任务的关系状态集合。
同时做出如下假设:
① 各观测任务之间具有独立性;
② 每个目标至多只能被观测一次;
③ 不考虑卫星设备故障;
④ 极端工况和特殊工况不予考虑。
基于上述定义和假设,多星观测任务规划的目的就是从各卫星的观测任务集合中选择一个子集,使得生成的规划方案在满足约束集合RES的前提下获取最大的目标观测收益。多星观测任务规划模型为:
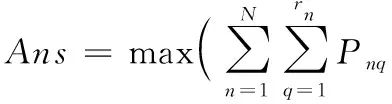
(1)
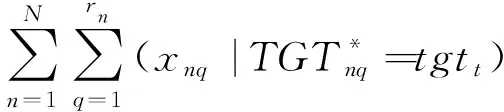
(2)
式(1)表示在约束条件下的最大观测收益;式(2)表示每个目标最多只能被观测一次。
2 约束条件分析
本文综合考虑载荷运行和平台运行,既要研究与观测任务相关的可见时间窗口的约束条件,还要考虑和平台运行有关的卫星轨道、热控、能量和姿态等多方面的约束,并逐一建立数学模型。
2.1 观测时间窗口约束
由于星载传感器的锥角和卫星侧摆角的限制[16-17],卫星只有在位于目标上方一定范围内时,才可对其观测。目标可被观测的某一时段,称为可见窗口。观测任务必须在可见窗口内完成,如图1所示。
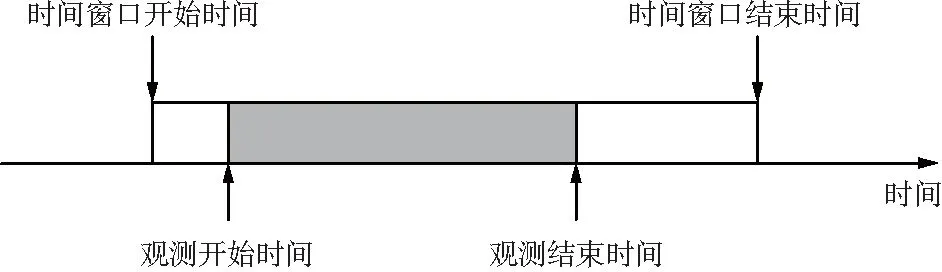
图1 观测任务时间窗口约束示意
本文利用Matlab和STK预先计算出所有卫星对各目标的可见窗口,对于观测任务tasknq,观测时间窗口约束可表示为:
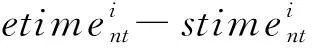
(3)
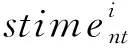
2.2 姿态调整约束
姿态调整冲突是针对卫星观测任务提出的,即卫星观测时姿态调整摆角不能超过设定值θ。目标在卫星轨道坐标系下的位置坐标为xs,ys,zs,则卫星俯仰和翻滚轴向的摆角θP,θR约束为:
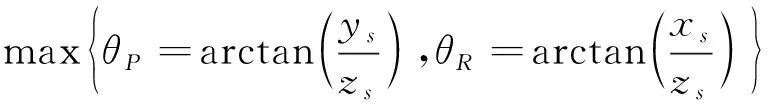
(4)
2.3 观测过渡时间约束
卫星在执行2个相邻任务时,需考虑到一定的过渡时间,以保证在此期间内调整好卫星姿态和成像仪器的工作状态,如图2所示。
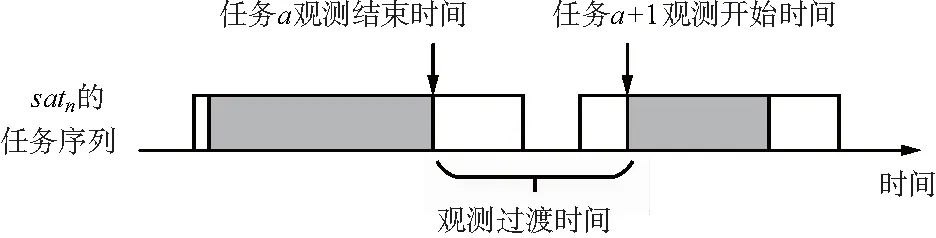
图2 观测过渡时间约束示意
以连续的任务a和任务a+1为例分析,设卫星俯仰轴向的调姿角速度参数为ω、翻滚轴向的调姿角速度参数为ψ,卫星完成前一观测任务的观测摆角为(θPB,θRB),取其后某一时刻对后续任务的观测摆角为(θP,θR),在连续姿态调整模式下,卫星的姿态机动时间Δta,a+1的计算公式为:
(5)
对于卫星satn的任务序列,前一个任务结束到下一个任务开始之间的时间间隔应该大于或等于一个过渡时间Ba,a+1,且过渡时间应该大于或等于卫星姿态调整时间Δta,a+1,观测过渡时间约束可表示为:
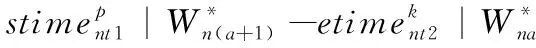
(6)
Ba,a+1≥Δta,a+1,
(7)
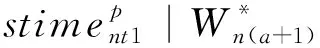
2.4 光照及能量平衡约束
对卫星电源系统有当圈能量平衡约束[18-19],即蓄电池组在地影期的放电量能在之后的光照期内得到完全补充,且为保证蓄电池寿命,单次在地影期的放电深度不超过20%,则能量平衡约束如下:
tCs,tCe∈[Tg,Td] ,
(8)
Ed≤min{Ec,0.2*EB},
(9)
式中,Tg,Td表示卫星光照期的起始时间和结束时间;Ed,Ec表示电池组在地影期的放电量、光照期的充电能;EB表示蓄电池容量。
2.5 存储资源约束
卫星每次存储的观测数据的大小不能超过存储设备当前的剩余容量Datafree,存储资源约束可表示为:
∀tasknq∈TASK,Datanq≤Datafree。
(10)
3 基于贪婪策略的遗传算法设计与实现
遗传算法是从代表问题可能潜在解集的一个种群开始,按照适者生存、优胜劣汰的原理,逐渐进化产生近似最优解的智能算法[20-21]。
3.1 编码
本文遗传算法采用二进制方式编码,如图3所示。染色体的每一位代表某一目标对应的某一时间窗口,取值为0或1,0表示该窗口不执行,1表示该窗口执行,染色体长度即为所有目标对于所有卫星的可见时间窗口数量。
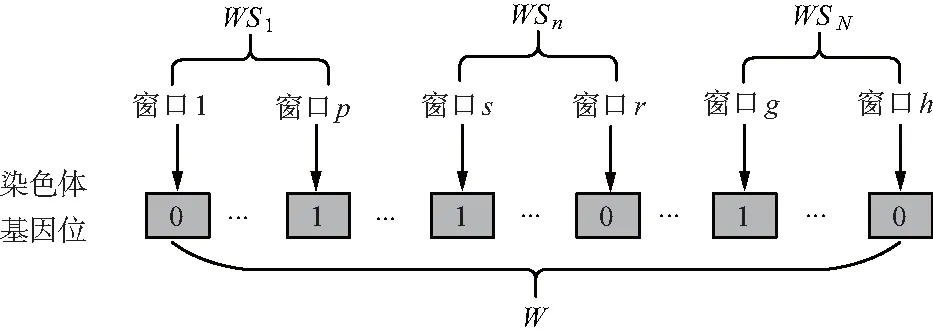
图3 遗传算法二进制编码方式
3.2 适应值函数
适应值是遗传算法选择的方向和标志,直接影响算法解决实际问题的性能和效率。适应值函数通常根据问题的优化目标来建立,通过评价种群中个体的适应度来选择个体。本文的适应值函数即为式(1)。
3.3 基于贪婪策略的种群初始化
由于遗传算法的搜索性能与种群的分布状态密切相关,而种群在遗传算法执行过程中的分布变化直接受其初始状态的影响,现有的方法大多通过随机产生初始种群,本文为了提高遗传算法的收敛速度和计算精度,采用基于贪婪策略[22]的赋值方法生成规模为M的初始化种群,具体方法如下:
① 将染色体按观测目标编号重新排序;
② 设置贪婪概率Pgreedy,计算需要置1的基因位数量T*Pgreedy;
③ 设置数组aT,乱序存放整数1,2,…,T,取前T*Pgreedy个数,即为染色体上需要被置1的基因位对应的目标编号;
④ 找到染色体上对应③中各目标编号的基因位,并在每个目标对应的基因位中随机选择一个置为1,剩余全部基因位置为0。
3.4 遗传算子设计
3.4.1 复制选择算子
选择算子主要实现父代种群中优秀个体和良好基因的保存,本文采用如下选择机制:对新产生的种群,按适应值从高到低排序,最高的个体直接进入交配池,剩余的个体按轮盘赌的机制进行选择,以提高适应值高的个体进入交配池的概率,尽可能淘汰适应值低的个体,且进入交配池的个体数量与种群数量相等。
3.4.2 交叉算子
由于双点交叉和三点交叉的方式在增加种群多样性的同时也增加了搜索的随机性,会导致算法收敛速度下降,因此选用单点交叉方法。随机选择交配池中的2个个体,随机选择一个交叉点,将2条染色体上位于交叉点之后的片段互换,即完成交叉操作。设交叉概率为Pcross,则执行交叉操作的个体数Mcross为:
Mcross=Pcross*M。
(11)
3.4.3 变异算子
变异算子能在种群个体间适应值区别较小时,增加种群的多样性,防止进化停滞,陷入局部最优。对进入交配池的个体,按一定的变异概率对染色体选择是否进行变异操作。当染色体被选中时,随机选择10%*T个基因位,改变该基因位原来的值,即由1变为0,或由0变为1。设变异概率为Pmuta,则执行变异操作的个体数Mmuta为:
Mmuta=Pmuta*M。
(12)
3.5 种群更新
对经过约束冲突处理的新个体计算适应值,若新个体的适应值比原个体的适应值高,则用新个体替换原个体进入到下一代种群中,否则保留原个体进入下一代。逐代优化,得到最优解。
3.6 算法实现
采用Matlab编程实现算法,步骤如下:
① 设置算法最大迭代次数MaxRun基于贪婪策略的种群初始化:采用3.3节中的初始化方法,对种群中的每条染色体按(0,1)编码方式进行编码;
② 冲突处理:对染色体上的基因位逐一进行冲突检查,没有通过冲突检查的基因位置为0;
③ 完成冲突检查和处理后,计算各个体的适应值,记录适应值最高的个体;
④ 判断算法停止条件,若满足停止条件,转向步骤⑤;否则按选择机制选择个体进入交配池,完成变异、交叉操作产生新个体,并进行种群更新得到下一代种群,返回步骤②;
⑤ 算法结束,获得最佳个体,输出相应的观测任务方案。
算法流程如图4所示。
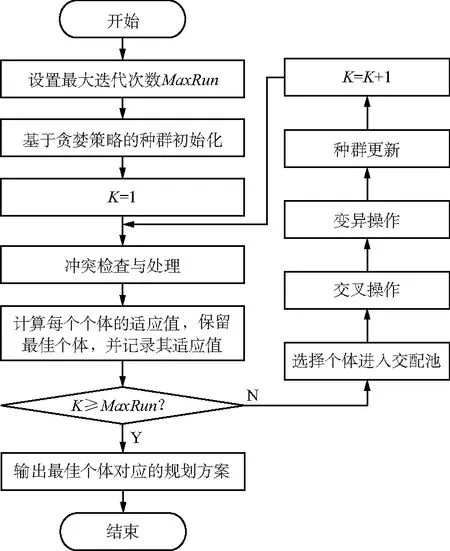
图4 算法流程
4 算例及分析
为了验证基于贪婪策略的遗传算法能在保证算法精度的前提下有效提高算法的收敛速度,采用模拟数据建立仿真算例,所有算法和程序用MATLABR2014a编程软件实现。对于目标、卫星的模型建立,时间窗口和卫星光照地影时段的预处理都通过STK9.2仿真软件实现,运行环境为Windows10 教育版,Intel Core i3-3220 CPU@3.30 GHz,8 GB RAM。
模拟数据产生过程如下:
① 在STK仿真场景中设定卫星数量为10颗,建立遥感卫星模型S1~S10来共同完成目标观测任务,其轨道建立参考了Orbview、Landsat、资源三号、风云一号和天绘一号等卫星的轨道参数;
② 利用Matlab随机在全球范围内建立50个地面观测目标点,并随机设定每个目标的收益值;
③ 设定多星观测任务规划周期为24 h;
④ 在STK中计算10颗卫星对50个地面目标的所有可见窗口W,部分观测窗口的数据如表1所示。
表 1 观测窗口数据表
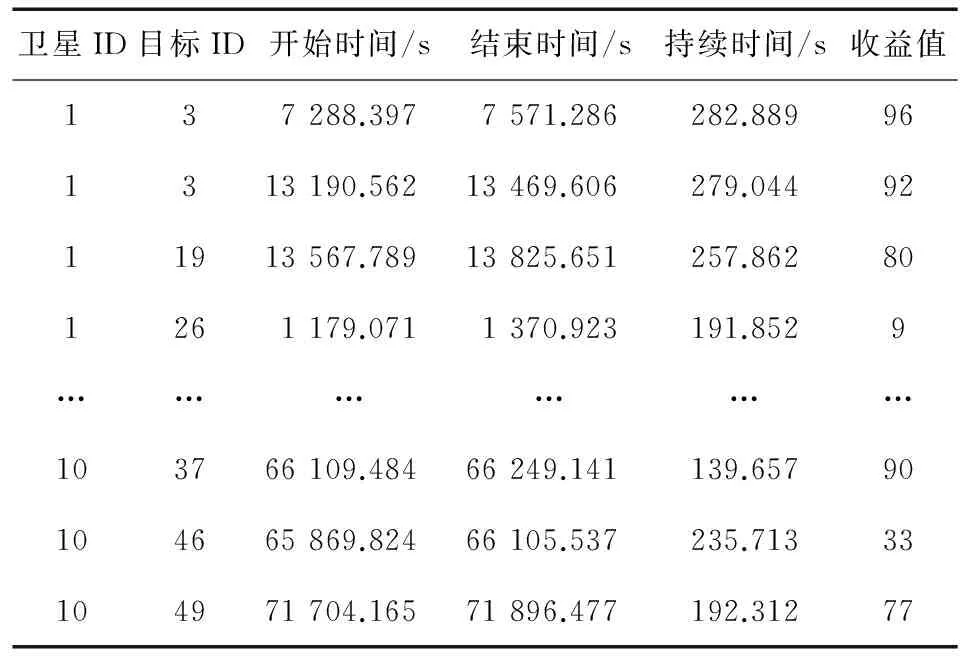
卫星ID目标ID开始时间/s结束时间/s持续时间/s收益值137 288.3977 571.286282.889961313 190.56213 469.606279.0449211913 567.78913 825.651257.862801261 179.0711 370.923191.8529………………103766 109.48466 249.141139.65790104665 869.82466 105.537235.71333104971 704.16571 896.477192.31277
算法的主要参数设置为:种群规模swarmNum=30,最大遗传代数MaxRun=50,交叉概率Pcross=1,变异概率Pmuta=0.1,贪婪概率Pgreedy=0.7。由于遗传算法本身具有一定的随机性,因此通过对多次运算(10次)的结果进行统计,比较基于贪婪策略的遗传算法和一般遗传算法在算法收敛精度和收敛速度上的性能,结果如表2和图5所示,基于贪婪策略的遗传算法典型的规划结果如图6所示。
表 2 计算结果
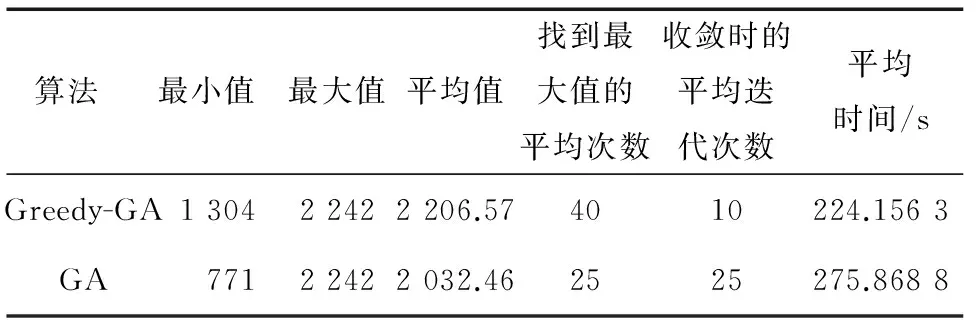
算法 最小值最大值平均值找到最大值的平均次数收敛时的平均迭代次数平均时间/sGreedy-GA1 3042 2422 206.574010224.156 3GA7712 2422 032.462525275.868 8
由表2可知,基于贪婪策略的遗传算法求解的任务规划方案与一般遗传算法求解的方案的收益值相同,说明基于贪婪策略的遗传算法能保证遗传算法原有的求解精度,同时,基于贪婪策略的遗传算法达到收敛状态的平均迭代次数为10,计算耗时224.156 3 s,而一般遗传算法达到收敛状态的平均迭代次数为25,计算耗时275.868 8 s,说明贪婪策略能有效提高遗传算法的收敛速度,减少计算时间。
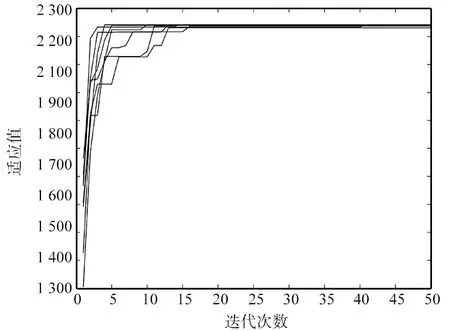
(a)基于贪婪策略的遗传算法
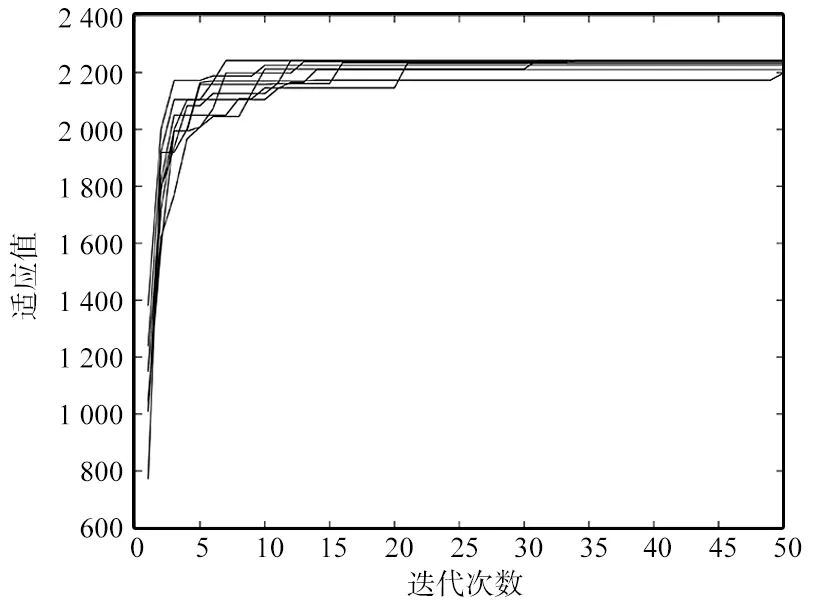
(b)一般遗传算法图5 10次计算进化曲线

图6 Greedy-GA的典型观测任务规划结果
5 结束语
针对一类观测任务具有优先级约束的多资源观测任务优化问题,建立了观测任务模型和观测任务规划模型,通过对各类复杂约束的深入分析和数学建模,设计了一种基于贪婪策略的遗传算法。仿真算例结果表明,该方法求解此类问题是合理且有效的,并且能在保证算法原有精度的前提下提高算法的收敛速度。
当然,目前对于如何更好地将贪婪策略与遗传算法有机结合方面的研究尚不充分,本文的研究也只是在提高算法求解速度方面取得了成果,今后的研究重点将放在如何将贪婪策略应用到遗传算法的选择、交叉与变异的过程中,以进一步提高算法的寻优能力和寻优速度。
