基于GARCH模型的中证股指期货日收益率波动的实证分析
2019-12-24
(四川大学 四川 成都 610000)
中证500股指期货于2015年4月16日上市,它的上市对防控金融风险、维护金融安全和提升金融竞争力意义非凡。而一个相对稳定的波动环境对国内经济稳定发展举足轻重,因此研究中证股指期货收益率的波动性具有重要的意义。
一、数据来源
本文选取2015年4月17日至2019年1月10日中证500股股指期货日交易收盘价为样本,共3 660个有效数据。对所得样本数据取对数,即Rt=ln(Pt)-ln(Pt-1),其中Rt表示中证股指期货t期收益率,Pt为t期收盘价[1]。本文数据来自CSMAR,实证分析结果通Eviews8.0计算获得。
二、数据的基本分析
(一)中证股指期货收益率的描述性统计分析
中证股指期货的日收益率的简单算术平均值为-0.000 3%,最大值为0.217 1%,最小值为-0.159 4%,标准差为0.043 8,峰度为4.811 69,偏度为-0.231 56。其中,偏度数值小于0,说明收益率序列左偏,其尾部分布较正态分布更长;而峰度数值大于3,说明收益率序列尖峰特征显著;J-B统计量高达142.055 3,大于在1%置信水平下的临界值,且P=0.000,拒绝原假设,即该时间序列不是正态分布。
(二)中证股指期货收益率的平稳性检验
利用单位根来检验该序列的平稳性,单位根检验主要是为了排除序列的伪回归现象。ADF的检验统计量的值为-11.717 86,其对应的P=0.000,拒绝原假设,即该序列没有单位根,该时间序列是平稳的序列。
(三)中证股指期货日收益率残差时序图
从图1中可以看出中证股指期货日收益率的残差时序图有着非常明显的波动聚集现象,这说明该序列波动较大,其残差项可能具有条件异方差性。
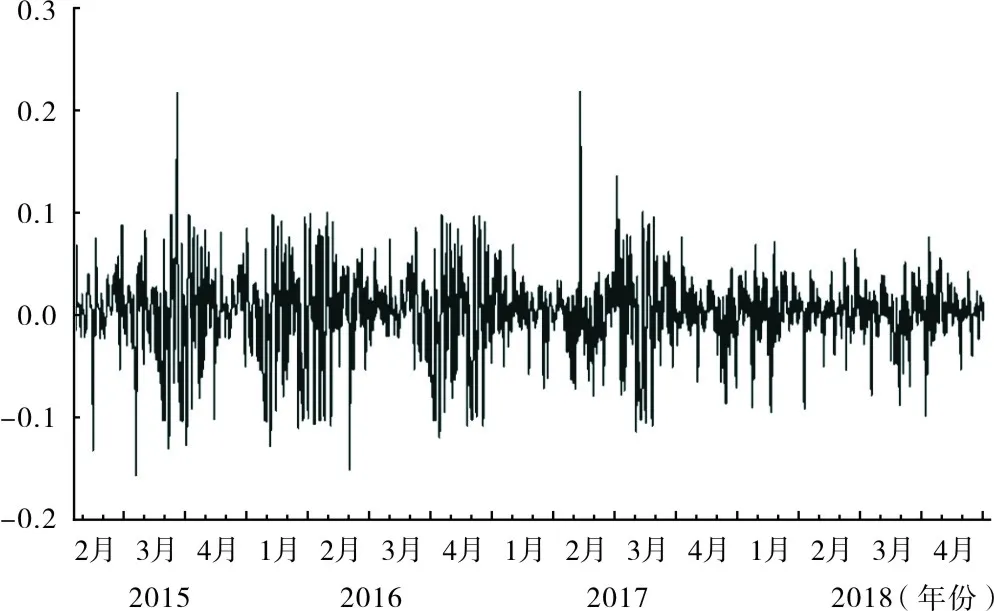
图1 中证股指期货日收益率残差时序图
(四)中证股指期货收益率序列ARCH效应的检验
因为考虑到残差可能具有异方差性,所以接下来需要进行ARCH-LM检验来考察该序列是否存在异方差性(ARCH效应)。从表1中可知,ARCH-LM检验结果显示P值显著为0,这说明了序列具有明显的异方差性,因此可以建立GARCH模型来进行分析。

表1 中证股指期货收益率的ARCH-LM分析结果
三、GARCH模型估计结果分析
GARCH模型中形式简单且应用最广泛的是GARCH(1,1)模型,本文对中证股指期货的收益率用GARCH(1,1)模型进行建模,并分别对扰动项为正态分布、学生t分布以及GED分布下的GARCH(1,1)模型进行参数估计,并从中选择拟合度最优的模型进行估计。

表2 三种分布下中证股指期货收益率GARCH(1,1)模型拟合结果对比
续表2

学生t分布常数项0.079 6410.044 0950.070 9ARCH项0.130 6940.031 9080.000 0GARCH项0.869 4480.025 3460.000 0GED分布常数项0.047 1880.043 4040.277 0ARCH项0.113 3520.027 6490.000 0GARCH项0.873 0580.028 8040.000 0
由表2可知,扰动项分布为正态分布时的GARCH(1,1)模型的均值方程的自变量在5%的显著性水平下显著,常数项的P值在5%的显著性水平下均显著。扰动项分布为学生t分布时均值方程的自变量在10%的显著性水平下显著,常数项的显著性在10%的显著性水平下显著。扰动项分布为GED分布时均值方程的自变量在10%的显著性水平下不显著,常数项的显著性在10%的显著性水平下不显著。而这三种分布的其他项(残差平方项、方差项)的P值在5%的显著性水平下均是显著的。由此可以看出正态分布下的GARCH(1,1)模型相较另外两种分布来说,拟合度更好。

表3 正态分布下GARCH(1,1)模型下的残差ARCH-LM检验
表3中对正态分布下GARCH(1,1)模型下的残差进行ARCH-LM检验,此时序列已不存在自相关性,可以证明正态分布下的GARCH(1,1)能够较好的消除残差所存在的异方差性,并且相对于另外两种分布下的GARCH(1,1)具有更优的拟合度。列出模型方程表达式为
条件均值方程
yt=0.107 997 965 556+0.987 920 431 39yt-1+εt
条件方差方程
