中学数学中的化归方法研究
2019-12-23董永霞
董永霞

化归方法是中学数学中最常用的一种简单的计算方法。这种方法可以简化我们所学的问题,让我们的条理更加清晰,思路更加明确。拥有智慧头脑的数学家并不是直接的去观察问题解决问题,往往要对要解决的问题进行简单的变化与转变,一直到它的形式可以归化到某个我们以前遇到并已经解决的问题里面,也可以是比较熟悉的问题中。就是把千变万化的问题转变为相对于简单易懂的问题,把相对于麻烦的问题转变为简单的问题的形式,以便使其中的数量关系和立体形式更加突出和显眼,这才可以让我们从这个问题中找到突破口,从而运用我们简单的问题把原有的问题解決。三角恒等式,可以将高次三角函数降幂,化成容易积分的形式。所以我们在碰到两个因式相乘除、高次三角函数积分时,就要考虑用化归这种方法。
当我们在生活中遇到问题,需要我们去解决的时候,拥有智慧头脑的数学家并不是直接的去观察问题解决问题,往往要对要解决的问题进行简单的变化与转变,一直到它的形式可以归化到某个我们以前遇到并已经解决的问题里面,也可以是比较熟悉的问题中。把遇到的问题,经过改变成其它的问题,我们再对这个问题进行下一步的求解,原有的问题就可以在这个变化中得到正确的解答,答案显而易见。那么这种方法称之为中学数学中的化归方法。
一、化归应用实例
化归方法是我们数学中经常遇见的一种分析问题和解决问题的基本思想方法。那么它的做法在数学中通常是这样的:将一个不是特别基本的问题通过平移、旋转、伸缩、分解、变形、转换等多种多样的方式进行改变,把问题化归为另一个我们熟悉的简单的基本的问题,在这个基础上我们就可以把原来的问题解答出来。
1.化归在代数问题中的体现
化归的本质就是运用来来回回每个方法都不同的途径而达到从不知道的到知道的、从麻烦的问题到轻松的问题、从复杂到简单的转变。初中数学课本中每个考点都渗透着化归与变动思维。分式方程、无理方程和单一的高次方程是一元一次方程、一元二次方程的进一步加紧和强化。
2.化归在几何问题中的体现
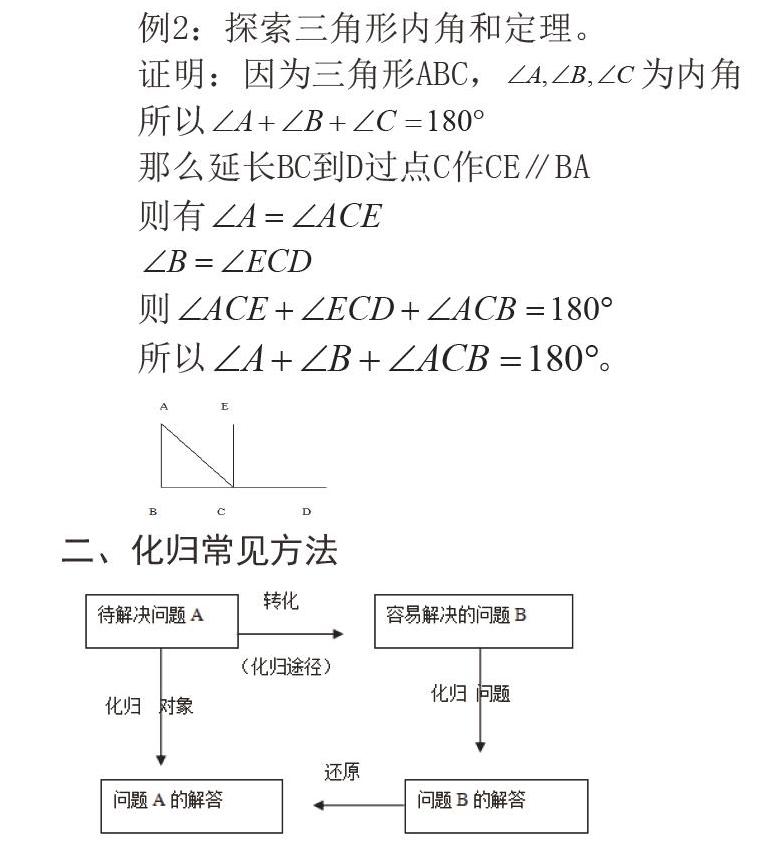
例2:探索三角形内角和定理。
证明:因为三角形点击并拖拽以移动,点击并拖拽以移动为内角
所以点击并拖拽以移动
那么延长点击并拖拽以移动到点击并拖拽以移动过点点击并拖拽以移动作点击并拖拽以移动∥点击并拖拽以移动
则有点击并拖拽以移动
点击并拖拽以移动
则点击并拖拽以移动
所以点击并拖拽以移动
点击并拖拽以移动
二、化归常见方法
点击并拖拽以移动
1.数列问题的转化
数列可以看成是定义在正整数集上的一种比较独特的函数模型,数列中恒成立的难题往往都是转化成我们经常用到的函数的方法来解决。在每年的高考中,数列是必考的知识点,所以应用广泛考生们也应具有一定的知识储备量,并且需要考生仔细的研究与解答。
例12:若数列点击并拖拽以移动满足点击并拖拽以移动为常数,则称数列点击并拖拽以移动为调和数列。已知数列点击并拖拽以移动为调和数列,且点击并拖拽以移动,则点击并拖拽以移动?
解析:从所熟悉的调和数列定义的知识观察,这个倒数数列满足等差数列的定义所以可以把这个问题转化成等差数列进行求解,进而求出前点击并拖拽以移动项和。从所学过的调和的定义可以清楚:数列点击并拖拽以移动为调和数列,则点击并拖拽以移动为常数,也就是数列点击并拖拽以移动为等差数列,现在点击并拖拽以移动为调和数列,则数列点击并拖拽以移动为等差数列,所以从点击并拖拽以移动,就可以得出点击并拖拽以移动
所以点击并拖拽以移动
2.整体化归
当我们遇到的问题繁琐以及麻烦的时候,需要分析遇到的问题独有的特征以及性质,从这些出发点具体的观察这个问题,繁琐的变为简单的,进而整体问题就可以化为简单的问题得到解决。
例4计算
点击并拖拽以移动 解析:令点击并拖拽以移动
进行整体变式,观察可见点击并拖拽以移动是个整体
原式=点击并拖拽以移动
点击并拖拽以移动
=点击并拖拽以移动
如果这个问题我们按照传统的方法乘开,我相信大部分人做不到,但是
运用化归就可以轻松简单的解决这个问题。
4.函数与方程之间的化归
对于我们所学过的自变量点击并拖拽以移动与因变量点击并拖拽以移动是相辅相成的,有的时候我们是想根据点击并拖拽以移动去求得点击并拖拽以移动,但是会发现问题往往不容易解答,那么就可以重新审查这个问题。
将一个不是特别基本的问题通过平移或者旋转或者伸缩或者分解或者变形或者转换等多种多样的方式进行改变,把这个问题让它化归为另一个我们熟悉的简单的基本的问题之后.学完一元一次方程简单的基础知识以后,当我们再次接触一元二次方程我们就是运用之前我们学过的一元一次方程因式分解来解答这个问题的.其它问题如代数问题化归为几何的问题,平面几何问题化归为三维几何问题的解决,任意角的正余弦函数问题化归为锐角正余弦函数问题来表示的习题就更多了。那么最后总的概括来说,其实所谓化归思想,正常便是指人们将以前无有碰到的题目转变成之前咱们遇到过得可能以前人们仍旧办理的问题中去,最终把原问题的成果求出来的一种可用的技术和方法要领。
