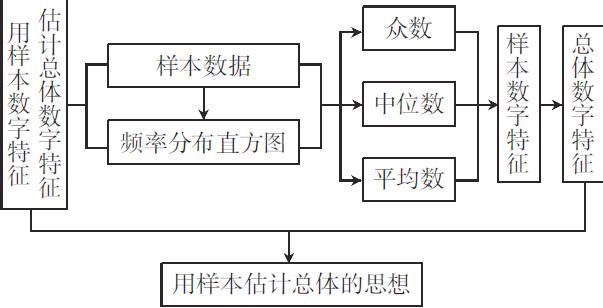
用样本的数字特征估计总体的数字特征

2019-12-23郭娇娇

新教育时代·教师版 2019年36期

郭娇娇

摘要：让学生深刻体会统计思想是重要的教学任务，在“用样本的数字特征估计总体的数字特征”教学中，统计思想的渗透也是教学的主要任务。本节课以扶贫工作为背景，以某贫困村小王书记的汇报工作为主线，使学生借助频率分布直方图，自主探究和合作交流，从形的角度估计样本的数字特征，从而估计总体的数字特征。

关键词：数字特征平均数中位数众数

高中数学必修三的第二章“统计”中，有“用样本的数字特征估计总体的数字特征”内容，主要为了让学生体会用样本估计总体的思想。在本节第一课时，传统的课堂只是让学生掌握用样本的频率分布直方图估计众数、中位数和平均数的算法，机械生硬，没有很好地从学生的认知角度出发。

抽象的数学理论与实际生活相结合，是新课程理念的必然要求;数学知识与时事政治的结合，是数学研究的实际意义所在。于是，在国家扶贫攻坚的大背景下，笔者从扶贫的角度，以小王书记对本村村民收入水平的分析入手，用部分村民的收入水平估计本村村民的收入水平，将国家政策和数学知识联系在了一起。[1]

以下是本节内容的教学思路展示。

一、创设情境，提出问题

党中央把贫困人口脱贫作为全面建成小康社会的底线任务和标志性指标。甘肃省某乡镇为了响应国家的号召，准备把脱贫攻坚作为一号工程。于是，镇领导准备考察本镇的居民收入情况，决定帮扶各村村民的45%。小王是该镇某村的村支书，需要向镇领导汇报本村的村民收入状况。这是他通过科学取样得到的本村20位村民的年收入（单位：万元）样本：[2]

0.3 0.7 0.8 1.2 2.8 1.8 1.9 1.3 1.6 1.3

1.3 1.8 1.7 1.6 1.9 1.3 1.4 2.2 2.3 1.6

思考并回答问题：

1.样本的众数，中位数，平均数是多少？

此问主要目的在于将身边的时事政治问题引入课堂，通过计算样本数据的三个数字特征，为随后进行的，由样本的频率分布直方图估计数字特征埋下伏笔。

2.如果小王要汇报本村村民收入情况，从以下三个角度分析，该怎样汇报？本村村民收入的平均水平，大部分村民收入的集中水平，位于中间水平的村民收入。

问题设计的目的在于，由样本数据得出数字特征，来估计本村村民收入的数字特征，引出本节课题，让學生初步体会样本估计总体的思想。也为下面用样本的频率分布直方图估计这三个数字特征的必要性埋下伏笔。

3.这三个数值主要刻画了数据的哪些特征？

平均数反映了数据的平均水平，中位数反映了中间数据的情况，众数反映了数据的集中水平。为用样本的三个数字特征估计总体的三个数字特征的优缺点埋下伏笔。

二、获得新知

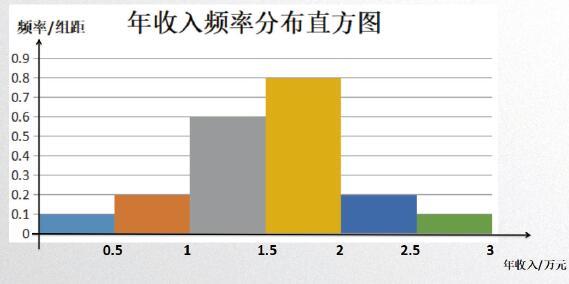
小王考虑，用具体的样本数据可以估计本村的居民收入情况，能否用样本的频率分布直方图来估计呢？图如下：

1.汇报本村村民的收入情况，需要考虑村民收入的哪些指标？

可以考察村民收入水平的众数，中位数和平均数本问主要为了创设用样本的频率分布直方图估计三个数字特征的情境，同时也让学生意识到，除了可以用样本数据的数字特征来估计本村村民的收入情况，还可以通过频率分布直方图估计。

2.如何从样本的频率分布直方图中估计众数？

因为众数是出现次数最多的数字，而频率分布直方图中最高矩形代表处于这个区间的数据最多，因而估计众数即为最高矩形的底边中点的横坐标。可以引导学生从众数的定义出发，寻找众数的估计值。[3]

3.在直方图中，中位数左右两边直方图的面积有什么关系？如何从频率分布直方图中估计中位数？

中位数左右两边直方图的面积相等。中位数的估计是本课的一个难点，学生在探讨中会遇到不同的问题，如：在直方图中为什么中位数左右两边小矩形的面积相等;中位数又该落在哪个区间，它是否一定落在最高小矩形框内等。在探究过程中通过引导学生复习中位数的概念及直方图的特征来寻找估计中位数的方法。

4.给定一组数据：1，2，2，2，5，8，4，4，4，4.如何来求其加权平均数？你能用频率分布直方图中估计平均数吗？

若直接让学生寻求平均数的估计方法较难，若先让学生求解某组数据的加权平均数，从而可以很容易地猜想可用每个矩形底边中点的横坐标乘以矩形面积来估计平均数。

5.小王很高兴地用大家估计出的这三个数字特征来汇报了本村村民的收入情况。他在汇报时说：我们村的人均收入就是1.525万元，年收入1.75万元的人是最多的，中间一部分村民收入1.5625万元。小王这样汇报有问题吗？为什么？

这样设计的目的是使学生明白用样本数据得到的众数、中位数、平均数只是总体数据的一个估计值，不是准确值，突出统计的思想方法。

6.小王用原始数据计算众数，中位数，平均数的时候，算出的是数字特征值是准确值还是估计值？用样本的频率分布直方图呢？为什么不一样？

原始数据得出的为准确值，用频率分布直方图得出的为估计值，因为频率分布直方图损失了一些样本信息。这样设计的意图还可以让学生了解到，获取数字特征可以从原始数据直接提取，也可以通过频率分布直方图获得，通过对比这两种方法，使学生明白从直方图中估计的数字特征虽然存在一定的误差，但直观、快速，也可以起到决策的作用。

7.如果换一个新的样本，数字特征会发生变化吗？为什么？如果所抽取的样本容量变大，样本的数字特征与总体的数字特征会有什么关系？

因为样本数据变了，所以估计出的数字特征业会发生变化，若样本容量增大，使得样本数据与总体数据相差越小，因而两者的数字特征值越接近。这样设计可以让学生进一步体会用样本估计总体时，样本选取所起到的作用。

笔者还预备用EXCEL软件随机取20个数，代表新样本，用此软件建立频率分布直方图，让学生估计，与之前样本的数字特征估计比较，这样处理可以直观地将结果表示出来。

8.小王汇报完毕后，准备回村落实扶贫政策。小王在路上就一直在想，要帮扶本村45%的贫困村民，那收入标准定为多少合适？

回归到原始问题的解决，让学生分析频率分布直方图，将学生所学知识内化为解决实际问题，不断深入，为合理制定决策提供依据。

9.得知镇里有扶贫政策，三位村民第一时间找到小王，各自反应自己的收入状况。老刘说，我一年中每月挣2000元的时候比较多，其他时候都不行;老赵说，我虽一年都在忙碌，也就在一年中间的那两三个月挣了点，每个月大约三四千;老张说，我这平均每月才勉强能挣1000元。如果你是小王书记，怎样确定谁为帮扶对象？

这是一个开放性问题，对学生的发言给予充分的肯定，让学生在发表自己意见的同时，深化对三种数字特征优点和缺点的认识和理解。

体会统计思维与确定性思维的差异，形成对数据处理过程进行初步评价的意识。

三、练习

例：下面是某市居民月用水量的抽样频率分布直方图，估计该市居民月均用水量的平均数和中位数.

本例题主要是用来解决课本上的生活用水问题。通过教材实例让学生感受统计在实际问题中的应用价值，强化学生在直方图中估计数字特征的具体方法。

四、总结归纳：这节课我们学到了什么？