旋翼类目标雷达回波建模及对微动特性影响分析
2019-12-23朱名烁周毅恒
朱名烁,韦 旭,周毅恒,黄 亮,杨 军
(空军预警学院,湖北 武汉 430019)
0 引 言
在现代战争中,旋翼类飞机如武装直升机、鱼鹰运输机等被广泛应用于各种军事行动,对旋翼类飞机的类型进行准确、快速的识别,有助于实现战场态势感知,对战争胜负起着举足轻重的作用[1,2]。然而随着电磁伪装、隐身材料等现代高科技技术的发展及应用,基于目标形状、雷达截面积(RCS, Radar Cross Section)等非运动特征的传统目标识别手段已难以满足目标属性识别的需求,这使得基于目标运动特征的识别显得尤为重要[3-9]。直升机旋翼叶片旋转导致的雷达回波的频率调制,即为“微多普勒效应”,不同旋翼直升机具有自身独特的微多普勒效应,因此若能对目标的微动信息进行精准提取,则可实现对不同旋翼类目标的分类识别。
文献[10]利用物理光学模型改进了直升机旋翼回波的微多普勒模型,并研究悬停状态下直升机旋翼叶片的叶片数量、叶片长度以及叶片转速对其微动特性的影响,但对旋翼运动状态的分析不够全面。文献[11]建立直升机旋翼做直线运动和俯仰运动的回波模型,但未考虑旋翼在三维自由空间的飞行状态变化。文献[12]建立了水平悬停状态下三种不同尖端类型的旋翼叶片回波模型,但未分析自由空间中旋翼的微动特性。文献[13]提出采用物理光学和等效电磁流法,对不同运动情况下旋翼RCS的时频特性进行了研究,但没有分析不同空间姿态角变化对旋翼类飞机微动特性的影响。文献[14]综述了近年来微动目标回波建模、微动特征提取和基于微动特征对雷达目标进行分类识别的研究现状,指出利用微动特征进行目标分类识别具有广阔的应用前景。
目前基于旋翼类目标微动特性的相关研究,在目标建模上均是对旋翼处于水平状态的这一理想情况下的建模,为使旋翼类目标回波建模及相关分析更加符合实际情况,建立了旋翼类目标在自由空间下的雷达回波模型,并在此基础上研究了旋翼叶片运动对目标微动特性的影响。首先将自由空间下旋翼的运动等效为滚转、纵摇、偏航这三种空间姿态,然后基于积分模型构建了旋翼在自由空间中的雷达回波模型,基于构建的模型,分别对旋翼在滚转、纵摇、偏航三种不同空间姿态角下的微动特性影响进行分析,最后通过仿真实验验证了模型的可行性和旋翼在不同情况下对微动特性影响的正确性。
1 旋翼叶片三维空间建模
旋翼叶片回波的积分模型[15,16]如图1所示。设雷达坐标系为(U,V,W),原点为O;参考坐标系(X,Y,Z)与雷达坐标系平行,它和目标坐标系(X′,Y′,Z′)的原点相同,均记作O′。设旋翼中心O′与雷达中心O的距离为R,其方位角和俯仰角分别为α和β,0°≤β≤90°,不失一般性,这里假设雷达主波束在α≤=0°时为照射目标。
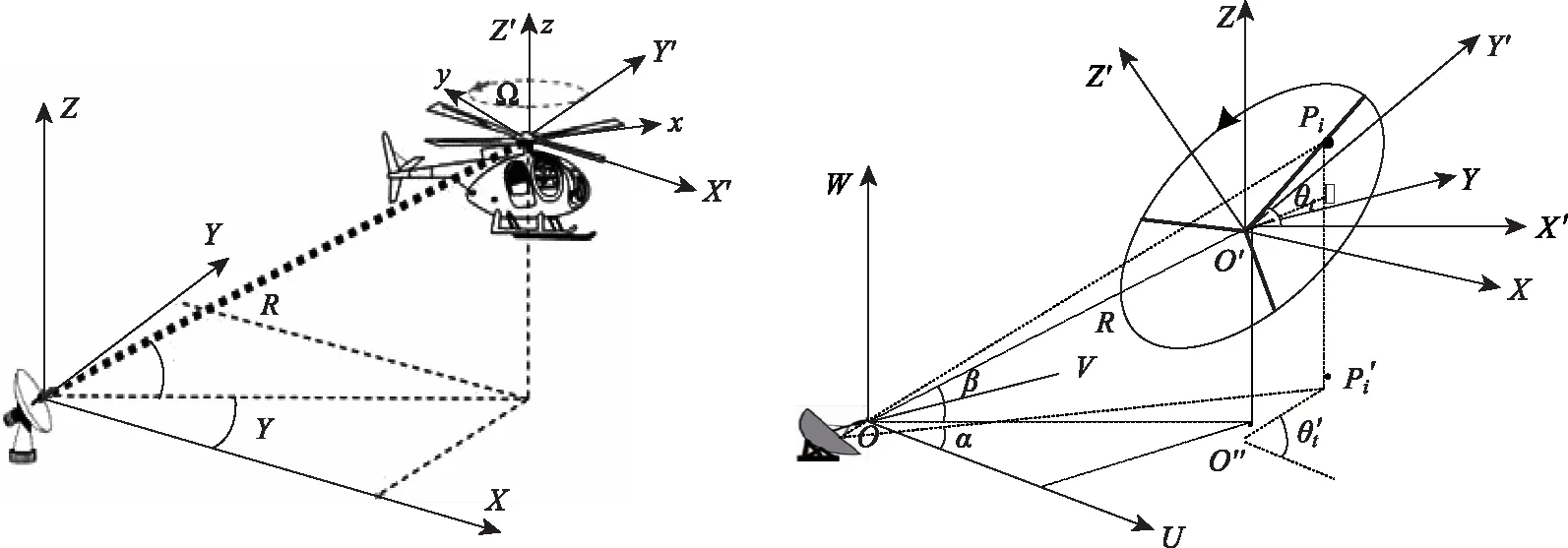
图1 直升机旋翼叶片的三维模型
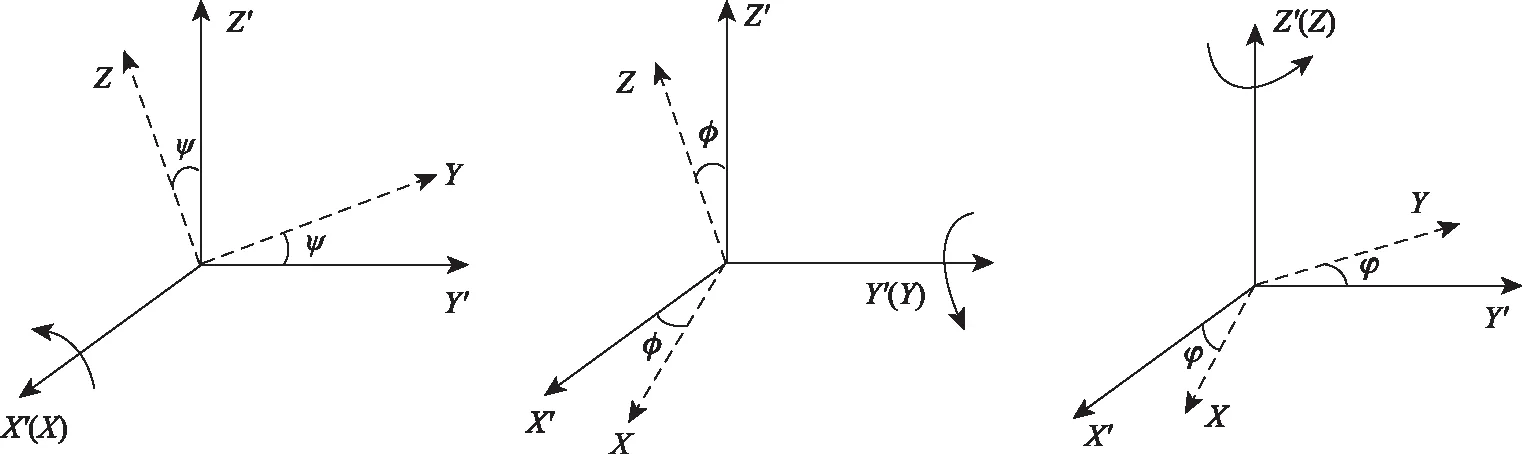
图2 滚转、纵摇和偏航旋转变化示意图
在研究旋翼直升机的飞行状态时,一般用欧拉角(ψ,φ,φ)[16]来表述直升机旋翼叶片的姿态变化,即目标坐标系(X′,Y′,Z′)与参考坐标系(X,Y,Z)的夹角为(ψ,φ,φ),夹角旋转变化如图2所示。其中ψ为X′轴与X轴的夹角,定义为滚转角;φ为Y′轴与Y轴的夹角,定义为纵摇角;φ为Z′轴与Z轴的夹角,定义为偏航角,且0°≤ψ,φ,φ≤90°。
经过空间姿态变化后,旋翼叶片上的任意一点在目标坐标系(X′,Y′,Z′)中的坐标通过旋转矩阵R转化到参考坐标系(X,Y,Z)中。其中,旋转矩阵R为
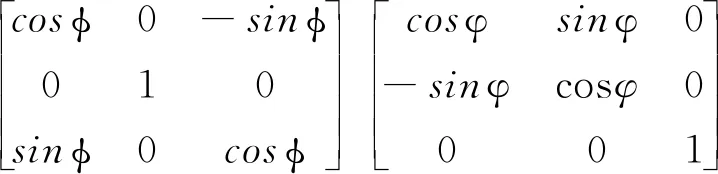
(1)
其中
(2)
(3)
(4)
在目标坐标系(X′,Y′,Z′)上,假设直升机旋翼叶片绕旋翼中心O′进行旋转,角速度为ω=2πfrot,旋转频率为frot。第一个旋翼叶片的初始旋转角为θ1,其中一个散射点Pi到旋翼中心的距离为xi(0≤xi≤l,l为叶片长度),经过时间t后旋转角变为θt=θ1+2πfrott。此时,Pi点在目标坐标系(X′,Y′,Z′)中的坐标为r0=[xicosθt,xisinθt,0]T,则转换到参考坐标系(X,Y,Z)的坐标为Rr0。
(5)
假设雷达发射的单载频信号为us(t)=exp(j2πfct),其中波长为λ=c/fc。对应图1,则存在如下关系
(OP′i)2=(OO″)2+(O″P′i)2+2OO″·O″P′i·
cos(θ′t)=R2cos2β+(x2+y2)+2Rxcosβ
(6)
PiP′i=Rsinβ+z
(7)
假设目标满足远场条件,则Pi与雷达的距离为
RPi(t)=[(OP′i)2+(PiP′i)2]1/2≈
R+xcosβ+zsinβ=R+xif1(t)
(8)
式中,f1(t)为第一个叶片的角度信息,表达式为
f1(t)=cosβ(r11cosθt+r12sinθt)+
sinβ(r31cosθt+r32sinθt)
(9)
此时雷达接收的散射点Pi的基带回波可表示为[15]
sPi(t)=σexp(-j4πRPi(t)/λ)
(10)
式中,σ为散射系数;ΦPi(t)=4πRPi(t)/λ为相位函数,其与旋翼叶片在三维空间中的状态有关。
对应式(10)中,由散射点Pi引起的瞬时微多普勒频率可表示为
(4πfrotxi/λ)[cosβ(r11sinθt-r12cosθt)+
sinβ(r31sinθt-r32cosθt)]
(11)
基于旋翼叶片所有散射点都会产生回波这一事实:从电磁散射的机理可知,叶片回波本质上是由叶片上所有散射点的回波在雷达视线方向上的矢量和,理论上可等效为对式(10)进行积分,因此可得第一个叶片上的散射点积分模型回波可表示为
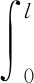
[-j2πlf1(t)/λ]sinc[2lf1(t)/λ]
(12)
由于旋翼上N个叶片的初始旋转角不同,则令第n个叶片的初始旋转角为θn(n=1,2,…,N),则有θn=θ1+(n-1)2π/N,此时旋转角θt=θn+2πfrott,角度信息为fn(t),fn(t)相比于f1(t),仅θt中包含的初始旋转角θn增加了2π(n-1)/N。此时,考虑初始旋转角与叶片数目后,总的回波可表示为
[-j2πlfn(t)/λ]sinc[2lfn(t)/λ]
(13)
式(13)即为旋翼在三维空间中的雷达回波模型。
当直升机处于远场水平悬停状态即理想情况时,滚转角ψ=0°、纵摇角φ=0°、偏航角φ=0°,式(13)变为
[-jπφ1(t)]sinc[φ1(t)]
(14)
式中,φ1(t)=2lcos[θ1+2π(n-1)/N+2πfrott]cosβ/λ。
式(14)结果与文献[16]中旋翼叶片处于水平悬停状态时的总回波结果一致,与旋翼类微动有关公开研究大多均基于式(14)这一模型下展开,该模型并未考虑目标(旋翼)运动对回波的影响,而由本文构建的式(13)雷达实际运动状态下的模型则更能反映目标运动在实际雷达回波中的变化情况。
在雷达观测条件下,旋翼叶片只有在在雷达视线方向(LOS)上产生距离差,才能在雷达回波中包含微多普勒信息,而垂直雷达视线方向上的转动分量对目标的微动特性没有任何影响。旋翼叶片的转动可以分解为沿雷达视线方向和垂直雷达视线方向上的两个转动分量,而自由空间下旋翼的运动都可等效为滚转、纵摇、偏航方向上的组合运动,这三个方向上的运动都会造成旋翼叶片沿雷达视线方向上转动分量的改变,从而影响旋翼的微动特性,因此,本文通过这三种姿态角的变化研究了旋翼在自由空间中的运动对目标微动特性的影响。
2 目标运动对目标微动特性的影响分析
旋翼类目标在自由空间中的运动可等效为滚转、纵摇、偏航三种姿态角的变化,因此,这里分别分析三种不同姿态变化角对目标微动特性的影响。理想情况即ψ=0°、φ=0°、φ=0°时,单个旋翼第n个叶片上第i个散射点引起的微多普勒频率为
(15)
此时,θt=θ1+2π(n-1)/N+2πfrott。当xi=l且sinθt=1时,叶片上的散射点引起的微多普勒频率峰值fdmax=4πlfrotcosβ/λ。
当俯仰角β=0°、cosβ=1时,旋翼叶片沿雷达视线方向的投影长度最大,此时旋翼的微多普勒频率峰值fdmax最大;当俯仰角β=90°、cosβ=0时,旋翼叶片沿雷达视线方向的投影长度为0,沿垂直于雷达视线方向的投影长度最大,此时旋翼的微多普勒频率峰值fdmax=0;且当俯仰角β在0°到90°范围内变化时,旋翼微多普勒频率峰值随俯仰角β的增大而减小。
2.1 滚转运动时对目标微动特性的影响
滚转运动即ψ≠0°、φ=0°、φ=0°时,对应的式(11)化简为
(16)
令
f(θt,β,ψ)=cosβsinθt+sinβsinψcosθt
(17)
考虑β∈[0°,90°],ψ∈[0°,90°]的情况,则
f(θt,β,ψ)=h(β,ψ)(cosΔsinθt+sinΔcosθt)=
h(β,ψ)sin(θt+Δ)
(18)
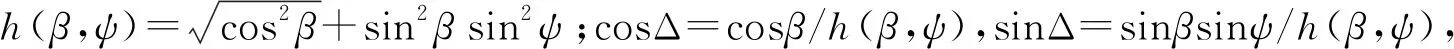

2.2 纵摇运动时对目标微动特性的影响
纵摇运动即ψ=0°、φ≠0°、φ=0°时,对应的式(11)化简为
(19)
由式(19)可知,纵摇角的变化会改变旋翼目标不同叶片上的散射点的微多普勒频率的绝对值大小。当xi=l、sin(θt)=1时,旋翼叶片引起的微多普勒频率最大,微多普勒频率峰值fdmax2=4πfrotlcos(β-φ)/λ,其大小与纵摇角和俯仰角都有关,可等效为改变了目标俯仰角,此时,直升机旋翼纵摇角的变化可等效于将其旋翼中心的俯仰角减小φ,且减小量不超过90°。
当0°≤φ<β时,随着纵摇角φ的增大,旋翼的微多普勒频率逐渐增大;当φ=β时,cos(β-φ)=1,旋翼的微多普勒频率峰值fdmax2达到最大值,其大小为4πlfrot/λ;当β<φ≤90°时,随着纵摇角φ的增大,旋翼的微多普勒频率逐渐减小。
2.3 偏航运动时对目标微动特性的影响
偏航运动即ψ=0°、φ=0°、φ≠0°时,对应的式(11)可化简为
(20)
由式(21)可知,当xi=l、sin(φ-θt)=1时,旋翼引起的微多普勒频率最大,其微多普勒频率峰值fdmax3=4πfrotlcosβ/λ,故偏航运动对旋翼的微多普勒频率峰值没有影响。偏航角变化可等效于改变旋翼不同叶片上的散射点的微多普勒频率随时间变化的旋转角,即旋转角θt更新为θt-φ=θ1+2π(n-1)/N+2πfrott-φ,故由于偏航运动,旋翼叶片的初始旋转角由θ1等效变化为θ1-φ,此时旋翼叶片的初始旋转角等效于减小了φ,且减小量不超过90°。
由上述分析可知,俯仰角及三种不同空间姿态角的改变相比于理想情况时,对直升机旋翼的微动特性的影响如表1所示。

表1 三种空间姿态角对旋翼微动特性的影响
3 仿真与分析
为了验证三种姿态角变化对目标微动特性影响的理论结果,本文通过仿真对旋翼三种姿态(滚转、纵摇、偏航)变化进行讨论分析。
仿真参数:叶片数:N=3,叶片半径长度:l=6 m,旋转频率:frot=4 Hz,散射系数:σ=1,方位角:α=0°,俯仰角:β=10°,第一个叶片的初始旋转角:θ1=0°,初始距离:R=15 km,观测时间:T=1 s,脉冲重复频率:PRF=4000 Hz。
(1)理想情况下的时频域特性
理想情况下即ψ=0°、φ=0°、φ=0°时,旋翼的时频域结果如图3所示。

图3 理想情况下旋翼的时频图
从图3可知,在时频域上,旋翼的微多普勒频率峰值为990.2 Hz,旋翼叶片的第一次正闪烁时刻[16]为0.06212 s,这两个值为下文研究相比于理想情况,不同空间姿态角对旋翼的微多普勒频率峰值以及初始旋转角变化的影响提供参考。
(2)滚转角对微动特性的影响
改变仿真条件中的俯仰角β,当俯仰角以10°的间隔值在0°~90°之间变化时,不同滚转角下旋翼的微多普勒频率峰值和初始旋转角变化的理论值如图4所示。
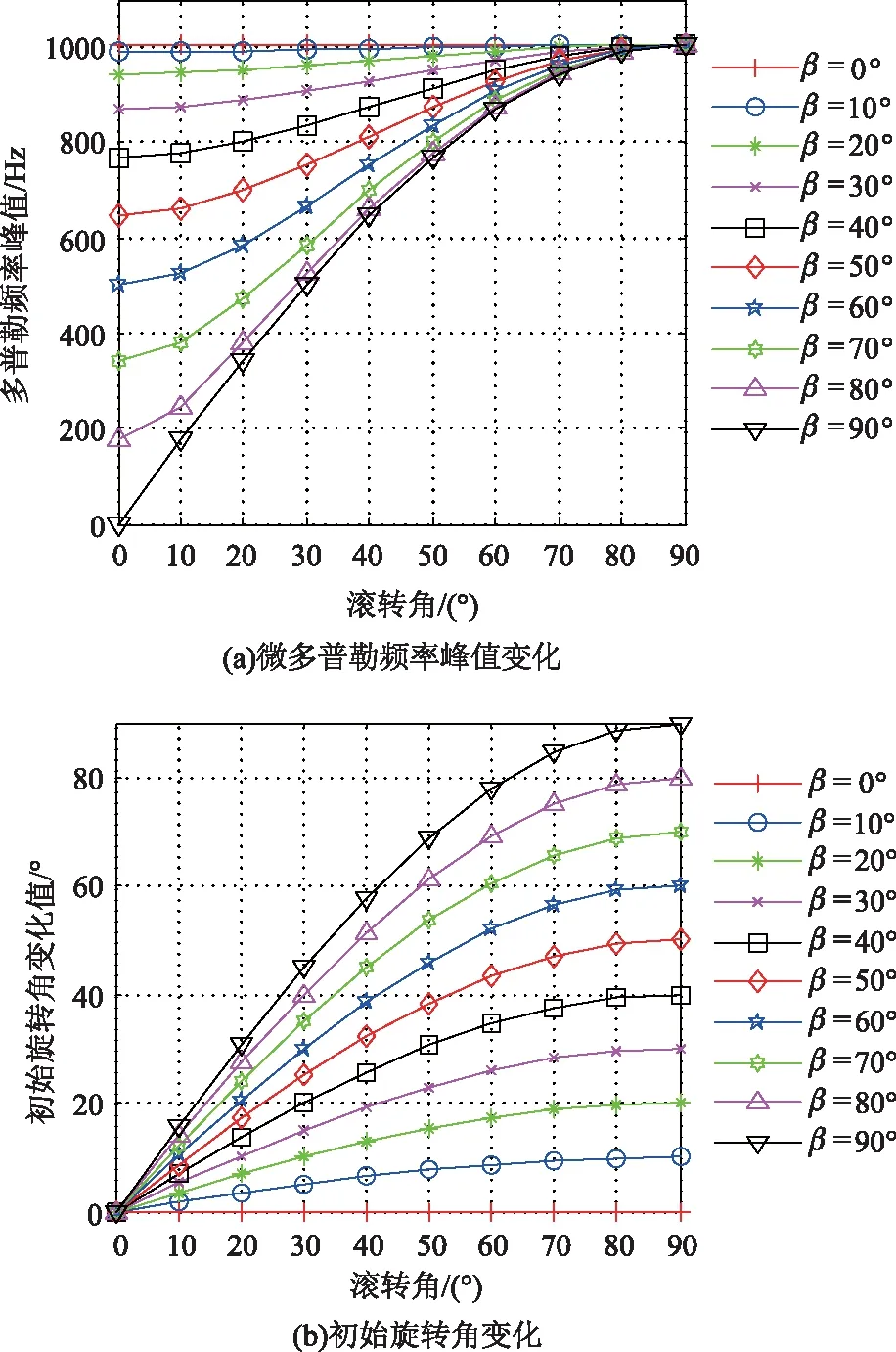
图4 滚转角对微多普勒频率峰值和初始旋转角的影响
从图4可知,在俯仰角为0°时,滚转角ψ的变化对旋翼叶片的微多普勒频率峰值和初始旋转角均没有影响;在同一滚转角下,随着俯仰角的增大,旋翼的微多普勒频率峰值越来越小,初始旋转角的等效增加值越来越大;在同一俯仰角下,旋翼叶片的微多普勒频率峰值和初始旋转角的等效增大值随着滚转角的增加而增大。当滚转角ψ较小时,俯仰角β的变化对旋翼的微多普勒频率峰值的影响较大;当滚转角ψ较大时,俯仰角β的变化对旋翼的微多普勒频率峰值的影响较小。
为验证上述理论结果,选取两个不同俯仰角β分别为10°和60°,不同滚转角下得到的旋翼回波经过短时傅里叶变换,得到旋翼的时频域结果,并分别读取旋翼的微多普勒频率峰值,该仿真结果与图4中的理论结果之间的对比如图5所示。
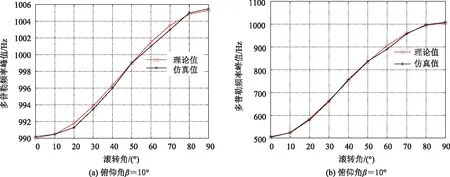
图5 不同俯仰角下,滚转角变化对应的微多普勒频率峰值的理论值和仿真值
从图5可知,当俯仰角β=10°和β=60°时,不同滚转角下旋翼的微多普勒频率峰值的仿真值和理论值基本一致,验证了理论分析的正确性。
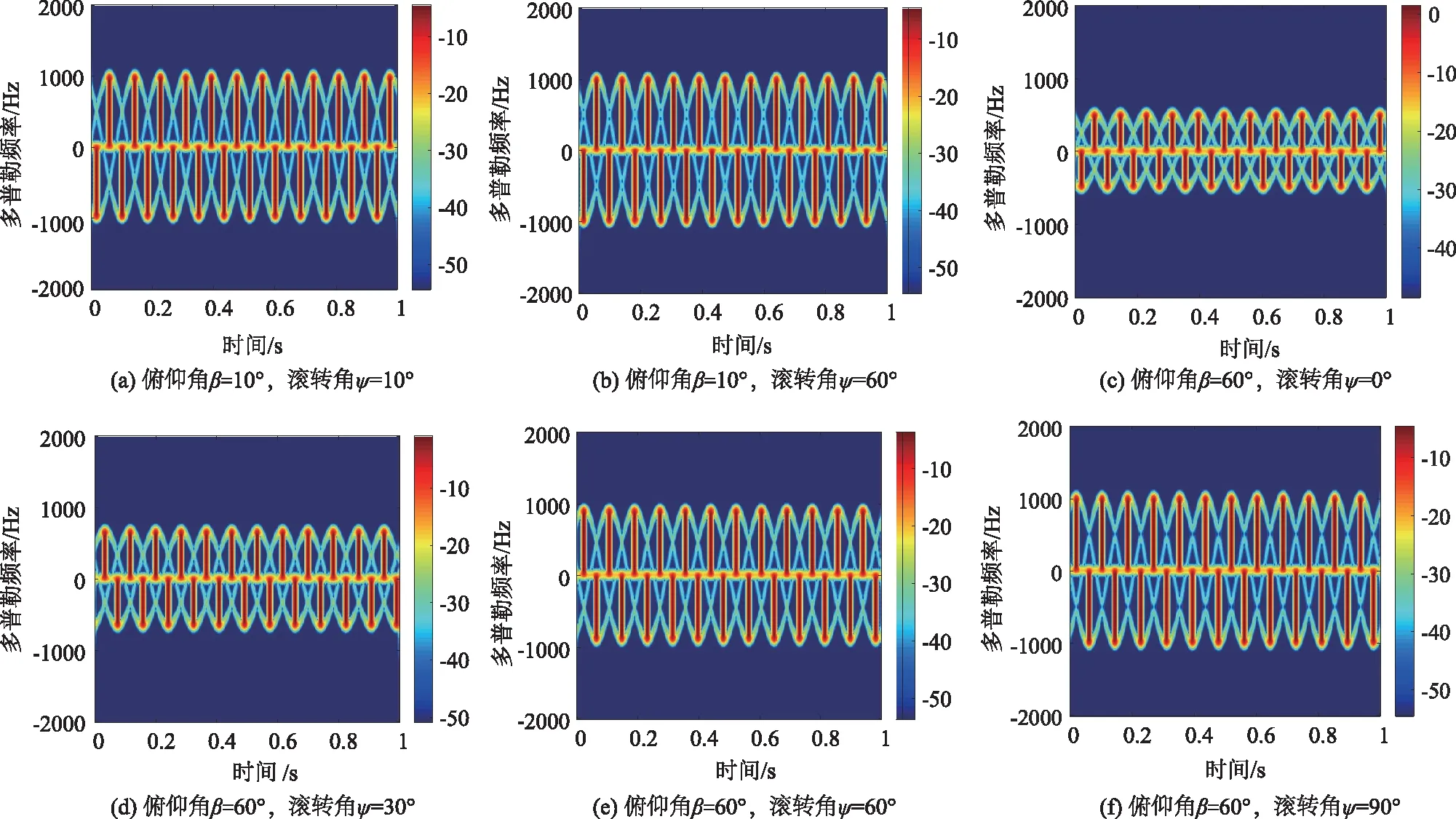
图6 不同俯仰角和滚转角下旋翼的时频图
当俯仰角β为10°时,给出滚转角ψ为30°和60°时旋翼的时频域结果,当俯仰角β为60°时,分别给出滚转角ψ为0°、30°、60°和90°时的时频域结果如图6所示。
对比图3和图6的结果可知,当旋翼中心的俯仰角β分别为10°和60°,且滚转角ψ以30°的间隔值从0°变化到60°时,旋翼的微多普勒频率峰值的变化情况如表2所示。
当旋翼中心的俯仰角β和滚转角ψ发生变化时,从图3和图6可知不同情况下叶片的第一次正闪烁时刻,根据旋转角差与时间差的关系式Δθ=2πfrotΔt,可得对应的初始旋转角差值,而根据上述的理论分析可知,对应的初始旋转角差的理论值Δ=arctan(tanβsinψ),所有结果如表3所示。

表2 微多普勒频率峰值随俯仰角和滚转角的变化情况

表3 初始旋转角差随俯仰角和滚转角的变化情况
由表2、3可知,滚转角变化既改变了旋翼的微多普勒频率峰值(其决定了微多普勒频率的变化范围),也改变初始旋转角(其决定了闪烁点的位置)。且当俯仰角β较小时,滚转角ψ的变化对旋翼的微多普勒频率峰值和旋翼叶片的初始旋转角的等效增加值的影响较小;当俯仰角β较大时,滚转角ψ的变化对旋翼的微多普勒频率峰值和旋翼叶片的初始旋转角的等效增加值的影响较大,与表1理论分析结果一致。
(3)纵摇角对微动特性的影响
不同纵摇角下的旋翼回波经过短时傅里叶变换得到旋翼的时频域结果,并分别读取旋翼的微多普勒频率峰值,该仿真结果与理论分析结果之间的对比如图7所示。

图7 纵摇角变化对应的微多普勒频率峰值的理论值和仿真值
从图7可知,不同纵摇角下,旋翼的微多普勒频率峰值的理论值和仿真值基本一致。当0°≤φ<β时,随着纵摇角φ的增大,旋翼的微多普勒频率逐渐增大;当纵摇角φ=β时,旋翼的微多普勒频率峰值达到最大值;当β<φ≤90°时,随着纵摇角φ的增大,旋翼的微多普勒频率逐渐减小。
选取纵摇角φ分别为30°和50°时,旋翼的时频域结果如图8所示。
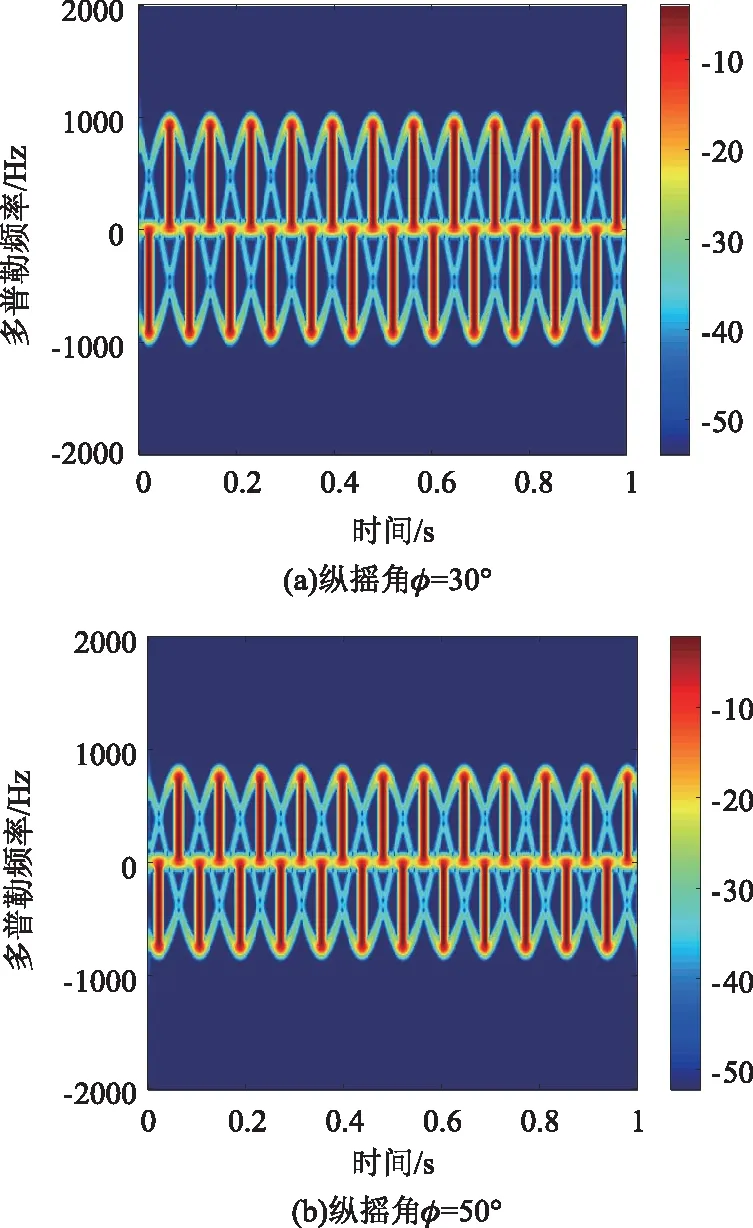
图8 不同纵摇角下旋翼的时频图

图9 旋翼的时频图
从图8可知,当纵摇角φ分别为30°和50°时,旋翼的微多普勒频率峰值的仿真结果分别为947.4 Hz 和776.9 Hz,而相对应的理论值分别为944.7 Hz和770.1 Hz,误差值分别为2.7 Hz和6.8 Hz,仿真结果和理论值基本一致。
改变仿真的初始条件,当旋翼中心的俯仰角β=0°,纵摇角φ=10°时,得到旋翼的时频域结果如图9所示。
对比图3和图9的结果可知,当旋翼中心的俯仰角β=0°,纵摇角φ=10°时,其时频域结果与旋翼中心的俯仰角β=10°,纵摇角φ=0°的时频域结果完全一样,验证了纵摇角的变化可等效为改变了目标的俯仰角β,且β减小了φ这一结论。
(4)偏航角对微动特性的影响
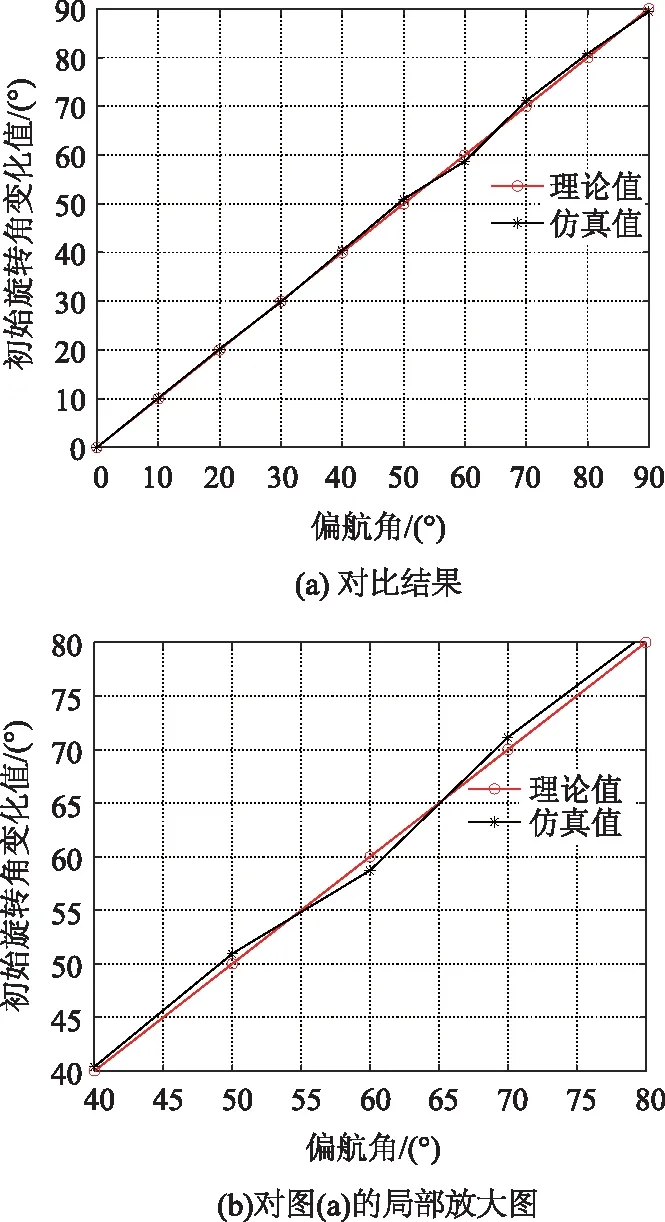
图10 不同偏航角下,初始旋转角变化的理论值和仿真值
不同偏航角下的旋翼回波经过短时傅里叶变换得到旋翼的时频域结果,分别读取旋翼叶片的第一次正闪烁时刻,通过计算与偏航角φ为0°时的第一次正闪烁时刻的时间差,然后基于初始旋转角变化值与时间差之间的对应转换关系式Δθ=2πfrotΔt,从而求得等效旋转角变化的仿真值,该仿真结果与理论分析结果之间的对比如图10所示。
从图10可知,不同偏航角下,旋翼叶片的初始旋转角变化的仿真值和理论值基本一致。选取偏航角φ分别为30°和60°时,得到旋翼的时频域结果如图6所示。
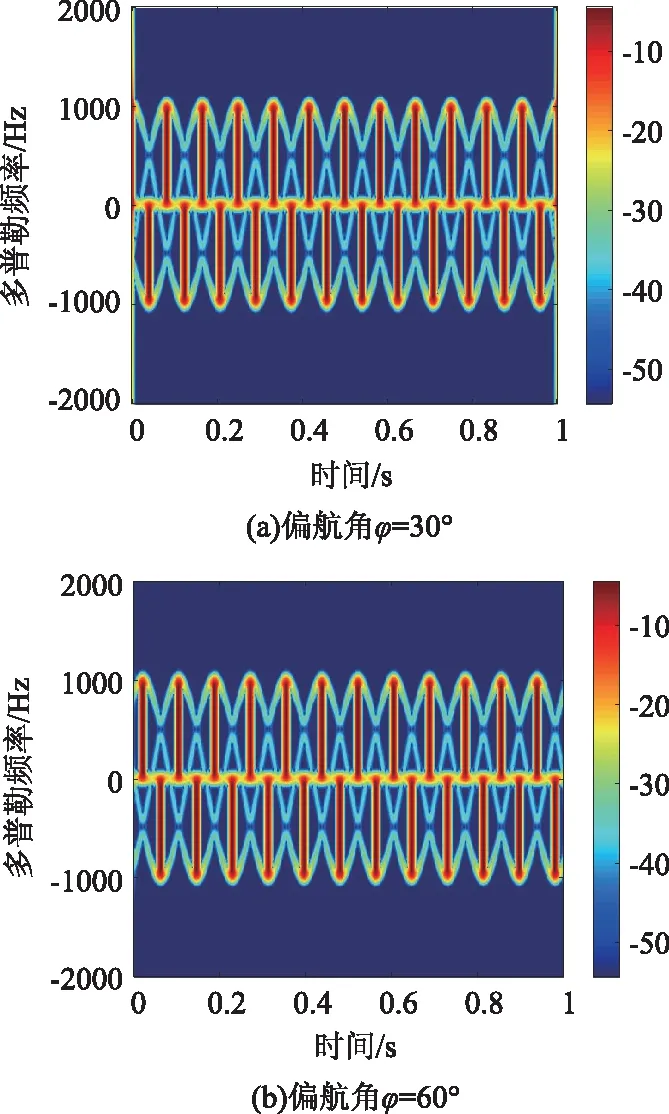
图11 不同偏航角下旋翼的时频图
从图11可知,当偏航角φ=30°和φ=60°时,叶片的第一次正闪烁时刻分别为0.08285 s、0.10289 s,与图3(b)相比,在对应的偏航角下,两者的时间差分别为Δt3=0.02073 s、Δt4=0.04077 s。根据旋转角差与时间差的关系式Δθ=2πfrotΔt,可得两种情况下旋翼叶片的初始旋转角差分别为Δθ3=29.8576°、Δθ4=58.7152°,误差值分别为0.1424°和1.2848°,与理论结果差别较小。故偏航运动等效于减小了旋翼叶片的初始旋转角,且减小值为偏航角φ的大小,同时使得时频图曲线沿时间轴上向右偏移,但对旋翼的微多普勒频率峰值没有影响。偏航角φ越大,旋翼叶片的初始旋转角的减小值越大。
4 结 语
本文针对现有旋翼类目标的相关研究大多是基于理想建模下展开的问题,为使旋翼类目标回波建模以及相关研究更接近实际,提出了旋翼类目标在自由空间下的雷达回波模型,并基于该模型就旋翼叶片运动对微动特性的影响进行了研究。首先,将旋翼叶片在自由空间中的运动等效为滚转、纵摇、偏航这三种空间姿态角的变化,并基于理想的积分模型构建了旋翼在自由空间中的雷达回波模型,然后从理论上分别分析了滚转、纵摇、偏航这三个维度姿态角的变化对旋翼微动特性的影响,最后通过仿真验证了该模型的可行性和旋翼类目标叶片运动对其微动特性影响的正确性。
