基于逻辑门限控制的汽车ABS仿真分析

王 琳，张安霞

(1.蚌埠学院 机械与车辆工程学院，安徽 蚌埠 233030；2郑州日产汽车有限公司，河南 郑州 450000)

防抱死制动系统(anti-lock braking system,ABS)可以根据车轮角速度信号计算车速、车轮滑移率及车轮角减速度，在汽车制动时可以自动调节车轮制动力的大小，改善制动效果，防止车轮抱死拖滑，提高制动稳定性[1-2]。目前ABS系统常用的控制方式主要有PID(比例积分微分)控制、模糊控制、最优控制、逻辑门限值控制等方式。其中，PID控制对被控对象参数变动较敏感，其控制精度高但适应性差[3-4]；模糊控制具有较强的鲁棒性，但调试整定参数较困难[4-5]；最优控制防抱死性能优异，但控制结构复杂，工业化推广困难[2-6]；逻辑门限控制不涉及具体的控制数学模型，能使复杂的非线性问题得以简化，系统实时响应性能佳，在ABS产品中应用较为广泛。

李刚等[7]考虑汽车制动时轴荷转移，制定出ABS逻辑门限值控制策略，并在试验台进行验证，结果表明该研究缩短了制动距离，提高了汽车制动时的方向稳定性；周东[8-9]等在研究ABS系统时汽车前后轴采用同一逻辑门限值控制，改善了制动效果，但其逻辑门限值控制法需要结合实际工况对过程参数进行选取和调整，才能达到较好的控制效果。本文以滑移率为主要控制参数、车轮角减速度为辅助参数，建立单轮汽车模型对ABS系统进行逻辑门限控制策略研究，并在MATLAB/Simulink模块中搭建ABS仿真模型进行仿真分析，以期改善汽车制动效果，提高行车主动安全性。

1 汽车ABS的数学模型

1.1 车辆动力学模型

汽车的实际制动过程非常复杂，为了便于研究分析，对其制动过程进行相关假设：①汽车左右完全对称；②忽略滚动阻力和空气阻力；③忽略制动时汽车的侧向运动和横摆运动。在上述假设下，将整车简化为单轮汽车模型[10]，如图1所示。

图1 单轮制动模型Fig 1 Braking model of the single wheel

根据受力分析，得到单轮车辆制动模型的微分方程如下：

车辆运动方程：m·u=-∑F

车轮运动方程：I·ω=Fb·r-Tb

地面制动力：Fb=Fz·φb

式中：m为1/4车辆质量，kg；u为车辆速度，m/s； ∑F为车辆纵向合力，N；I为车轮转动惯量，kg·m2；ω车轮角速度，rad/s；Fb为地面制动力，N；r为车轮半径，m；Tb为制动力矩，N·m；Tp为车轴推力，N；φb为制动力系数；Fz为车轮地面法向反作用力，N。

1.2 车辆轮胎模型

轮胎模型有很多种，如魔术公式、刷子模型、双线性模型等，实际制动时，轮胎的制动力系数和滑移率并非简单线性的关系。为了使结果更加贴合实际，文中采用双线性模型为研究对象[11-13]，将制动力系数-滑移率关系曲线简化后得到如下表达式：

式中：φb为制动力系数；φp为峰值附着系数；φs为滑动附着系数；S为车轮滑动率；ST为最佳滑动率。

1.3 制动系统模型

车辆制动系统主要包括传动机构和制动器两部分。传动机构主要是液力传动，零部件之间又存在间隙和摩擦，液压油也有压力损失，建模时如忽略电磁阀弹簧的非线性特性和压力传递延迟的影响，将其简化为一个电磁阀和积分环节，则传递函数为：

式中：G(s)为传递函数；T为时间常数，s；s为自变量。

假设车辆制动器为理想元件，建立制动器数学模型。该模型主要反映制动力矩和制动系统液压之间的关系，方程如下：

Tb=kf·p

式中：Tb制动力矩，N·m；kf制动系数，N·m/kPa；p制动液压力，kPa。

1.4 车轮滑移率、制动效能数学模型

汽车制动一般分为3个阶段：第一个阶段轮胎留在地面上的印痕和轮胎花纹基本一致，车轮近似于纯滚动阶段；第二个阶段轮胎留在地面上的印痕逐渐模糊，在滚动时存在滑动的成分；第三个阶段轮胎在地面上的印痕看不出花纹，车轮完全处于抱死拖滑的状态。为了评价滑动成分的多少，提出了滑移率的概念，其表达式如下[14-15]：

式中：S为车辆滑动率，m/s；u为车轮中心速度,m/s；r为没有地面制动力时的车轮滚动半径，m；ω为车轮的角速度，rad/s。

遇到紧急情况时，汽车能否迅速降低车速直至停车，常用制动效能来评价。制动效能的量化指标主要有制动减速度和制动距离。

装有ABS的车辆制动减速度为

abmax=φp·g

式中：abmax为车辆制动减速度，m/s2；φp为峰值附着系数；g为重力加速度，m/s2。

制动距离表达式为

2 汽车ABS控制

2.1 汽车ABS控制原理

由图2汽车制动力曲线可以看出：在OA段随着滑动率的增加制动力系数迅速增加；过A点后增加缓慢，在B点达到峰值，此时对应的滑动率为15%～20%；随着滑动率进一步增加，制动力系数开始下降，直至滑动率为100%，车轮呈抱死状态，此时侧向附着系数极小，在受到轻微侧向干扰时，车辆将会出现甩尾、侧滑等不稳定现象。

图2 制动力系数—车轮滑移率曲线[14]Fig 2 Curve of braking force coefficient-wheel slip rate

汽车ABS系统以制动力曲线为基础进行控制，其工作原理如图3所示。制动时将滑动率控制在15%～20%之间(低于20%为制动稳定区域，高于20%为制动非稳定区域)，此时地面纵向附着力和侧向附着力均较高，其实际制动过程接近于理想制动过程，可以保证制动时车辆操纵的稳定性。

图3 ABS工作原理图Fig 3 Working principle diagram of ABS

2.2 汽车ABS逻辑门限控制策略

2.2.1 以滑移率参数为主的控制策略

在实际制动时，当滑动率高于设定值20%时，ECU发出指令减小制动力，此时制动压力调节器减小液压制动下的制动压力；当滑动率低于设定值15%时，ECU将发出增大制动力信号的指令，通过制动压力调节器增大制动管路压力；如果滑移率在设定限制以内，压力调节器将处于保压状态。实际制动过程中，压力调节器在ECU的调节下以一定频率进行增压、保压、减压的不断切换，使滑动率维持在理想范围内，以便缩短制动距离，提升制动时方向的稳定性。

2.2.2 以车轮角减速度参数为辅的控制策略

ECU根据车轮的车速传感器信号计算车轮的实际角减速度，并将其作为控制制动力输出的依据，使其尽可能接近车速折算角减速度。制动时，当车轮角减速度达到门限值时，ECU输出减小制动力信号，液压制动系统降低制动压力；当车轮转速升高至角减速度门限值时，ECU输出增加制动力信号，制动液压力增加。

汽车ABS的控制策略如图4所示。

图4 汽车ABS逻辑门限控制策略Fig 4 Automobile ABS controller strategy with logic threshold

3 汽车ABS系统仿真及结果分析

3.1 汽车ABS系统仿真

MATLAB是美国MathWorks公司开发的数学软件，主要用于算法开发、数据可视化、数据分析等领域，主要包括MATLAB和Simulink两大部分。其中Simulink提供了一个动态系统建模、仿真和综合分析的集成环境，无需大量的编程，可以通过简单直观的操作构建出复杂的系统。

本文以某轿车ABS系统为研究对象，在MATLAB/Simulink模块中搭建仿真模型(图5)进行仿真，模型具体参数见表1。仿真时设置最佳滑动率为20%，仿真时间为5.0 s，当制动车速降为零时，仿真结束。

图5 汽车ABS逻辑门限控制模型Fig 5 Automobile ABS controller model with logic threshold

表1汽车单轮模型参数
Table1Parameters of the single wheel model of automobile

参数参数值单轮汽车质量/kg300初始制动车速/(m·s-1)30车轮滚动半径/m0.295车轮的转动惯量/(kg·m2)0.7轴距/m2.6

为了更好地评价基于逻辑门限控制方式的汽车ABS效果的优劣，文中对无ABS系统的单轮汽车模型也进行了仿真(在仿真模型中Ctrl为1时，车辆装有ABS系统；Ctrl为0时，车辆未装ABS系统)，仿真结果如图6～图9所示。

3.2 汽车ABS系统仿真结果分析

图6、图7分别为无、有ABS系统的单轮汽车模型角速度变化曲线。从图6、图7可以看出：未装ABS系统的汽车制动进行到0.8 s时，车轮角速度和车轮折算角速度严重偏离，车轮开始抱死拖滑；装有ABS的车辆，车轮角速度和车轮折算角速度基本一致，当制动进行到4.25 s时车轮角速度才逐渐降为零。

图6 无ABS系统的单轮汽车模型角速度变化曲线Fig 6 Angular velocity variatioon curve of the single wheel vehicle model without ABS system

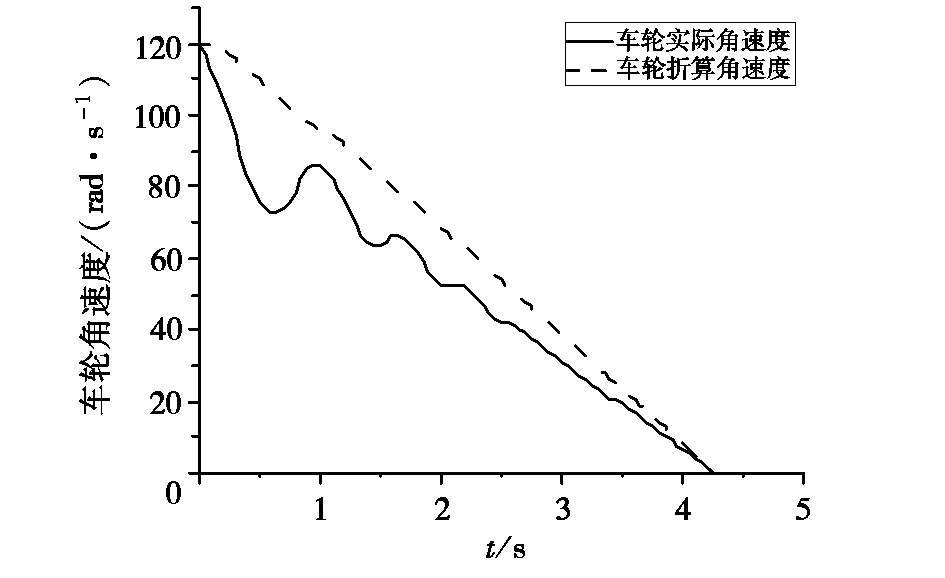
图7 有ABS系统的单轮汽车模型角速度变化曲线Fig 7 Angular velocity variatioon curve of single wheel vehicle model with ABS system

图8为汽车无、有ABS系统控制的滑动率变化曲线。从图8可以看出：随着制动过程的进行，车轮滑动率逐渐增加，但未装ABS系统的汽车，制动进行到0.3 s后，滑动率迅速升高，直至车轮完全抱死；装有ABS系统的汽车，滑动率一直在20%上下波动，当制动时间为4.25 s时，滑动率才开始快速升高，此时车轮的角速度已经很低，达到0.12 rad/s时，制动稳定性较好。

图8 单轮汽车模型滑动率变化曲线Fig 8 Slip rate variatioon curve of the single wheel automobile model

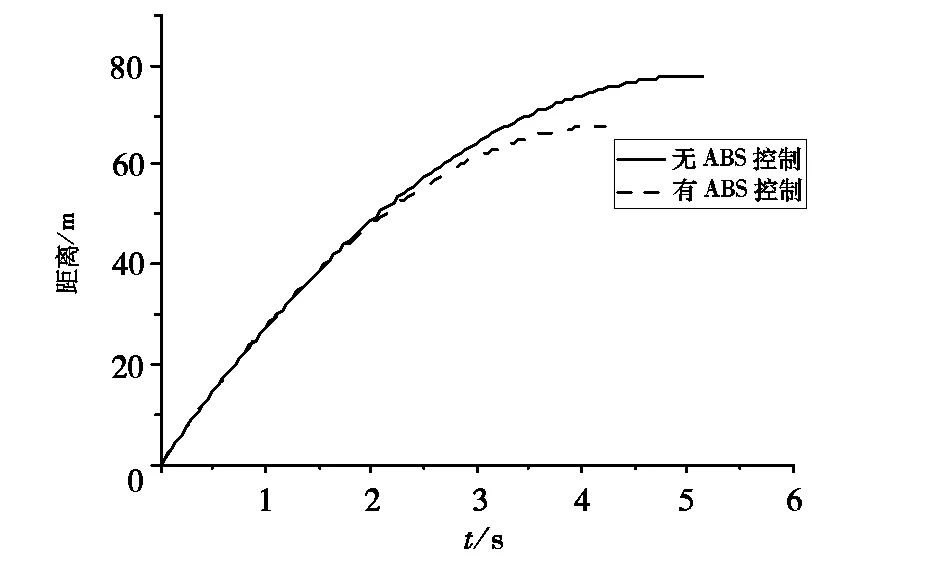
图9 单轮汽车模型制动距离变化曲线Fig 9 Braking distance variatioon curve of the single wheel automobile model

图9为汽车无、有ABS系统控制的制动距离变化曲线。从图9可以看出，加装ABS系统的汽车制动距离比未装ABS系统的汽车缩短10.14 m，缩短了13.02%，制动效果较好。

综合以上分析，在汽车制动过程中，车轮滑动率进入到非稳定区域时，车轮趋于抱死；在ABS系统中采用逻辑门限控制方式设置门限值，通过ECU的控制、压力调节装置会迅速降低制动管路压力，使车轮滑动率恢复到稳定区域内，保持制动时方向的稳定性；装有ABS系统的车辆还能有效缩短制动距离，在紧急制动时，保证行车的主动安全性。

4 结束语

(1)基于逻辑门限参数综合考虑车轮滑动率和车轮角速度的变化，以逻辑门限控制方式对汽车ABS系统进行设计，通过门限值的设置，在制动过程中实时控制制动管路压力的大小以调节制动力的大小。

(2)在MATLAB/Simulink模块中搭建汽车ABS液压制动系统模型并进行仿真分析。为了综合评价汽车ABS系统效果，对未装ABS系统的单轮汽车模型进行对比仿真，验证了采用逻辑门限方式对汽车ABS系统设计具有较好的应用效果。

(3)汽车ABS系统可以使车轮滑移率一直维持在20%左右，与未装ABS系统的单轮汽车模型相比，制动距离缩短了13.02%。