链式深耕机刀具切削土壤数值模拟
2019-12-21张富贵黄化刚符德龙吴雪梅
卫 韦,张富贵,黄化刚,符德龙,吴雪梅
(1.贵州省烟草公司毕节市公司,贵州 毕节 551700;2.贵州大学 a.工程训练中心;b.机械工程学院,贵阳 550025)
0 引言
为解决南方山区多年使用微耕机进行土壤耕整,造成土地耕层浅,浅耕层下形成板结的犁底层,影响作物根系下扎,水、肥入渗困难等问题[1-2],研制出了适合南方山区复杂地形条件使用而且耕深可以打破犁底层的深耕机—小型履带式链式深耕机,其耕深可以达到25cm。ANSYS/LS-DYNA软件具有同时利用ANSYS软件强大的前后处理功能和LS-DYNA软件非线性求解功能的特点,能够有效地进行切削过程的有限元模拟分析[3-6]。近3年来,越来越多的专家学者采用这个软件对各种刀具切削土壤进行仿真模拟。例如,2017年,中交疏浚技术装备国家工程研究中心有限公司的杨晨等人采用LS-DYNA软件对绞刀切削土壤进行仿真模拟[7];2016年,西南大学的韩煜杰采用LS-DYNA软件对旋耕刀切削土壤进行仿真模拟[8]。2015年,华南农业大学的齐龙等人采用该软件对松土刀切削土壤进行有限元仿真[9]。本文基于ANSYS/LS-DYNA软件,采用LSTC公司开发的LS-PREPOST专用后处理器直接读取LS-DYNA计算生成结果,进行数据汇整及二次运算,进行了所研制深耕机刀具切削土壤的显式动力学分析[10-11]。经过对切削过程的研究,对单个刀具切削土壤过程进行分析,旨在揭示单个刀具-土壤的工作机理。同时,对其切削力以及切削深度进行了分析,验证了所研制出的深耕机可以达到25cm的设计耕深要求,同时也为分析切削力及拟为深耕机刀具与土壤相互作用的数值模拟方面的研究提供参考。
1 材料与方法
1.1 土壤本构理论
通常情况下,在给土体施加外载荷后其状态与所施加载荷的数值有着密不可分的关系。当所施加载荷小到足以忽略时,土体就会呈现出线弹性。如果外载荷不间断的持续加大时,土体所受应力就会高于弹性极限,此时土体的应力应变关系就会发生变化,不再是之前所呈现出的理想弹性状态,土体的一些部分开始向塑性状态转变。判断是否转变为塑性状态的条件称之为屈服条件。但是,有些土壤类型,即使达到屈服条件以后也并不发生破坏,而且继续对于加载依然能够承受,此时应力和应变之间的关系就会发生改变,不再是之前所呈现出的线弹性关系,而是开始强化,应力和应变之间的关系变为非线性关系[12]。本文的土壤模型所采用的屈服准则是Mohr-Coulomb条件(莫尔-库伦屈服准则)和Drucker-Prager条件。
1)Mohr-Coulomb条件(见图1)。Coulomb给出了土体每一受力平面上所受的切应力大小达到极限值时,土体就逐步踏入屈服极限状态,其表达式为
τ=c+σntanφ
(1)
式中φ—土壤内摩擦角;
σn—每一受力平面上的正应力;
n—受力面外法线方向;
c—粘聚力。
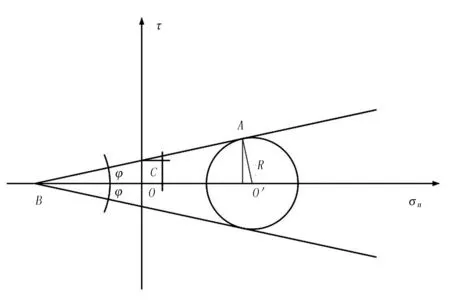
图1 Mohr-Coulomb条件Fig.1 Mohr-Coulombconditions
后经Mohr.优化,推广到一般情况。Mohr-Coulomb条件也可以写成以下形式
(2)
在三维情况下,该条件可表示为
(3)
式中I1—应力张量的第1个不变量;
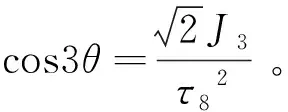
Mohr-Coulomb条件在主应力空间为一棱椎体。
2)Drucker-Prager条件。Drucker和Prager提出可对Mohr-Coulomb条件的改进。其表达式为
(4)
(5)
(6)
实际上,I1=σ1+σ2+σ3是发生体积变化时的静水压力状态,如果比较大的静水压力作用于金属材料上时,由于其体积发生了非常小的改变,故不考虑在内,式(4)中的首项就删掉。对于土体来讲,多数时候下的体积改变是显而易见的。
1.2 数值模拟中所采用的土壤本构模型
为使刀具切削土壤数值仿真模拟更接近现实,所以土壤本构关系的选用尤为重要。本文选择的土壤模型材料为MAT147(MAT_FHWA_SOIL),其应用的是修正的Drucker-Prager塑性模型,如图2所示。Mohr-Coulomb与Drucker-Prager屈服表面的结合使模拟结果更接近真实破坏平面(同时避免了Mohr-Coulomb屈服准则的奇异性)[13]。
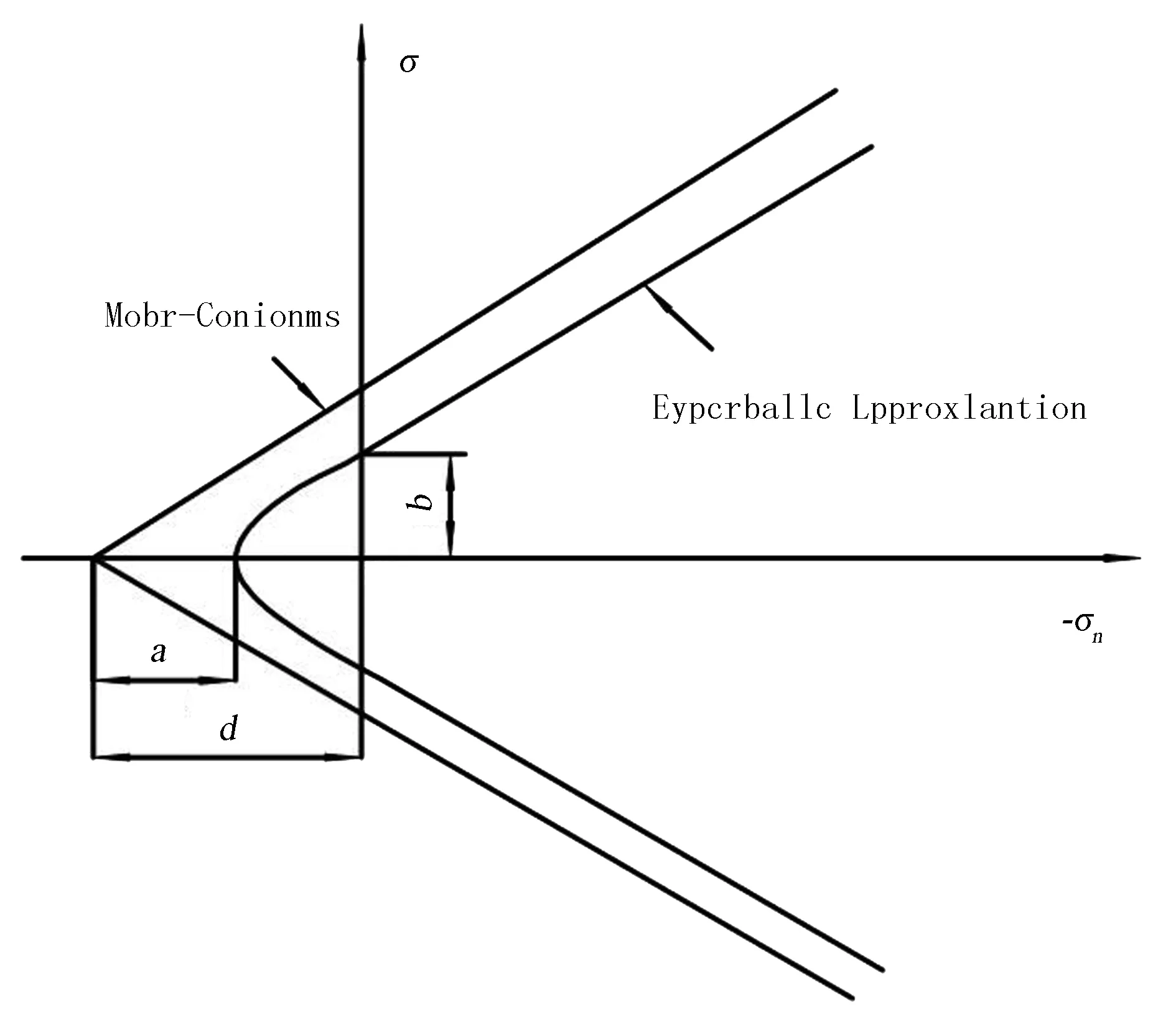
图2 修正的Drucker-Prager塑性模型Fig.2 Modified Drucker-Prager plastic model
Abbo和Sloan给出了修正的Drucker-Prager塑性模型。当剪切力微乎其微时,屈服面就成为平滑的面,同时压力轴成直角关系。改善后的Mohr-Coulom屈服准则式为
(7)
式中P—压力;
φ—内摩擦角;
J2—应力偏张量的第2个不变量;
K(θ)—张量平面角的函数;
c—粘聚力。
当Ahyp=0时,式(7)为标准Mohr-Coulom屈服面。针对这种仿真来说,Ahyp取值就要低于ccosφ,参照Lewis文献,通常依据下式选取,则
(8)
2 深耕刀具切削土壤模型确定
2.1 具切削土壤初始位置模型
选择土壤MAT147的本构模型建立了土壤模型,通过SolidWorks搭建了深耕刀具的三维模型,将其另存为.x-t格式的文件,再导进ANSYS—LS-DYNA中。图3为刀具与土壤初始位置模型。
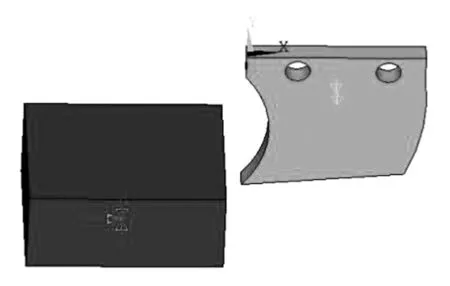
图3 刀具切削土壤初始位置模型Fig.3 Tool cutting soil initial position model
2.2 ANSYS—LS-DYNA中模型参数设定
现将刀具切削土壤模型的模拟过程中相关参数的设定如下:
1)设定ANSYS—LS-DYNA中的SOLID164作为土壤和刀具的单元类型,为防止在网格划分过程中出现沙漏能会影响结果的准确性,本文采用的是全积分算法。将刀具用手动来划分有限元网格, 划分单元数为3 880个;将土壤用手动来划分有限元网格,划分单元数为55 000个。图4为刀具切削土壤模型的网格划分。

图4 刀片切削土壤模型的网格划分Fig.4 Mesh generation of blade cutting soil model
2)通过实际情况的分析,选取了MAT-147塑性模型和MAT-GIRID刚性体材料模型分别作为本文仿真模拟研究的土壤模型和刀具模型。表1和表2是土壤模型及刀具模型的材料参数。

表1 土壤材料参数Table 1 Soil material parameters

表2 刀具材料特性Table 2 Tool material characteristics
3)将刀具和土壤分别设置为接触Part和目标Part,把刀具与土壤之间的接触类型设置为面面侵蚀接触,此接触选项能够做到如果在出现表面单元失效的时候,程序能够自动定义新的接触面。
4)设置刀具沿X方向平动切削土壤,大小为1.1m/s。
5)刀具切削土壤模型的约束设置。在本文中,需要对土壤及其刀具加上相关的约束条件;将土壤底部设置为全约束,目的是使得土壤模型在施加切削力后可以真实的体现土壤的变形状态。由于要满足刀具沿x轴方向平动切削的要求,所以对刀具z轴方向进行了全约束,图5为刀具切削土壤模型施加约束。
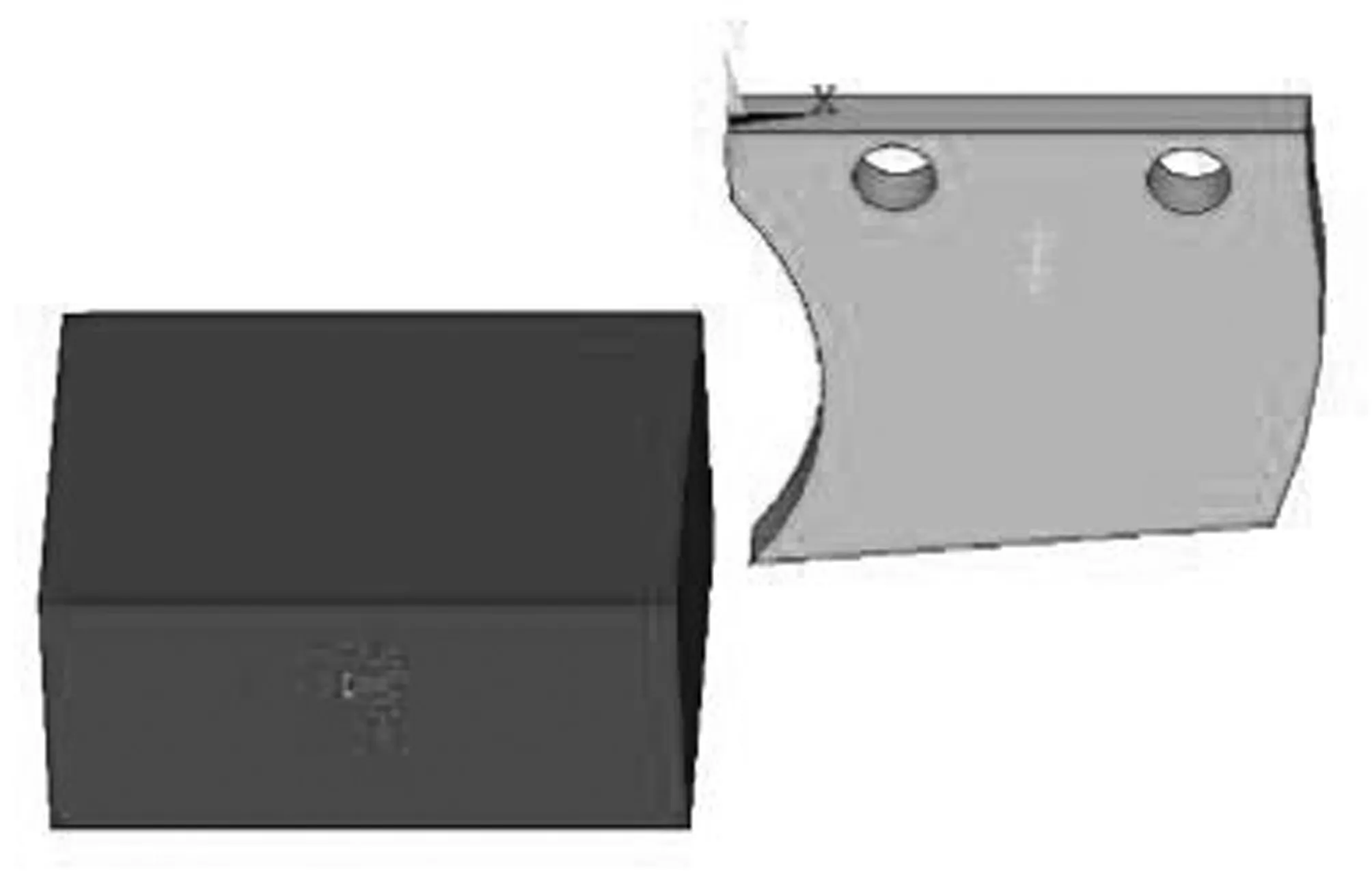
图5 刀具切削土壤模型施加约束Fig.5 Tool cutting soil model imposing constraints
2.3 切削模型k文件输出及其关键字修改
将在SolidWorks中建好的刀具模型导入ANSYS-LS-DYNA前处理器中,并在其中建立好土壤模型,通过选定单元类型、定义刀具和土壤的材料模型、划分网格、指定接触类型、对边界条件进行设置、定义刀具初始速度以及设置求解控制设置等一系列操作后生成K文件;然后,根据模拟研究的要求对生成的K文件进行关键字的更改;将修改好的K文件保存并导进ANSYS-LS-DYNA求解器中进行运行求解。
2.4 ANSYS-LS-DYNA求解器求解
将K文件进行修改或替换后调入ANSYS-LS-DYNA求解器中进行运行计算,整个求解过程所用的时间大约7h。
2.5 结果后处理
用ANSYS-LS-DYNA自带的后处理器LS-PREPOST导入求解器运行后生成的d3plot结果文件,进行可视化处理观察动态仿真过程并进行分析。
3 结果与讨论
3.1 刀具切削土壤过程分析
在仿真过程中,刀具沿直线切削土壤。刀具以速度1.1m/s沿前进方向(即仿真中X方向)对土壤进行切削。图6为1个周期的作业过程。观察1个切削周期,发现切削过程中刀具刀尖首先接触土壤,该处土壤受刀具切削力作用发生剪切破坏从而凹陷变形;随着刀片继续前进,刀具对土壤的接触面也随之增大,挤压变形也更加剧烈,刀具不间断地进行土壤切削,对土壤的破坏效应也急剧加大,然后还未与刀具接触的土壤受前面土壤的挤压也依次发生变形效应。

(a) 0.03s

(b) 0.06s

(c) 0.09s图6 切削过程组图Fig.6 Cutting process diagram
3.2 切削力分析
刀具切土壤的过程是非常复杂的,因而过程是不易控制的。专家学者经大量研究发现:土壤的破坏一般情况下是剪切破坏。因为土壤本身特性,自身有强度的存在,在刀具刚开始与土壤接触发生相互作用时,刀具上的切削力小于对土壤破坏的强度,此时土壤只会产生挤压变形,随着切削过程的进行切削力也会随之增强。当切削力不断增大突破土壤的破坏强度时,土壤开始遭到瓦解,刀具所受切削力此时不再继续增加;当所有土壤都被刀具切削过后,刀具切削力立即减下来并渐渐趋于水平状态。
如图7是刀具切削土壤的一个周期的切削力变化情况,选择了4个时间段的Von Mises Stress图像。其等效应力大多数情况下是聚集在土壤变形最大处,出现这种情况的原因是由于刀具随着切削土壤的深度增大,产生的切削力自然也随之增强导致的。土壤变形最大处成为应力集中区域。当刀具分别切削到0.03、0.06、0.09、0.12s时,对应的最大等效应力分别为1.831e-06GPa,1.258e-06GPa,6.955e-07GPa,6.535e-07GPa。

(a)

(b)

(c)

(d)图7 1个周期内刀具切削土壤的Von Mises Stress等效应力云图Fig.7 The Von mises stress equivalent stress clouds of cutting soil in a cycle soil in a cycle
根据不同时刻刀具切削土壤的等效应力变化规律用曲线画出,如图8所示。观察发现:在刀具刚进入土壤的一段时间,等效应力随时间的延长而持续加大,随之刀具一步步将土壤结构损坏,然后等效应力就下降。在切削到0.09s后,刀具切削土壤的切削力渐渐处于水平状态,变化幅度不大,等效应力也慢慢保持不变。这时,刀具所受等效应力主要是土壤被破坏后对刀具的阻力、粘滞力以及土壤重力。
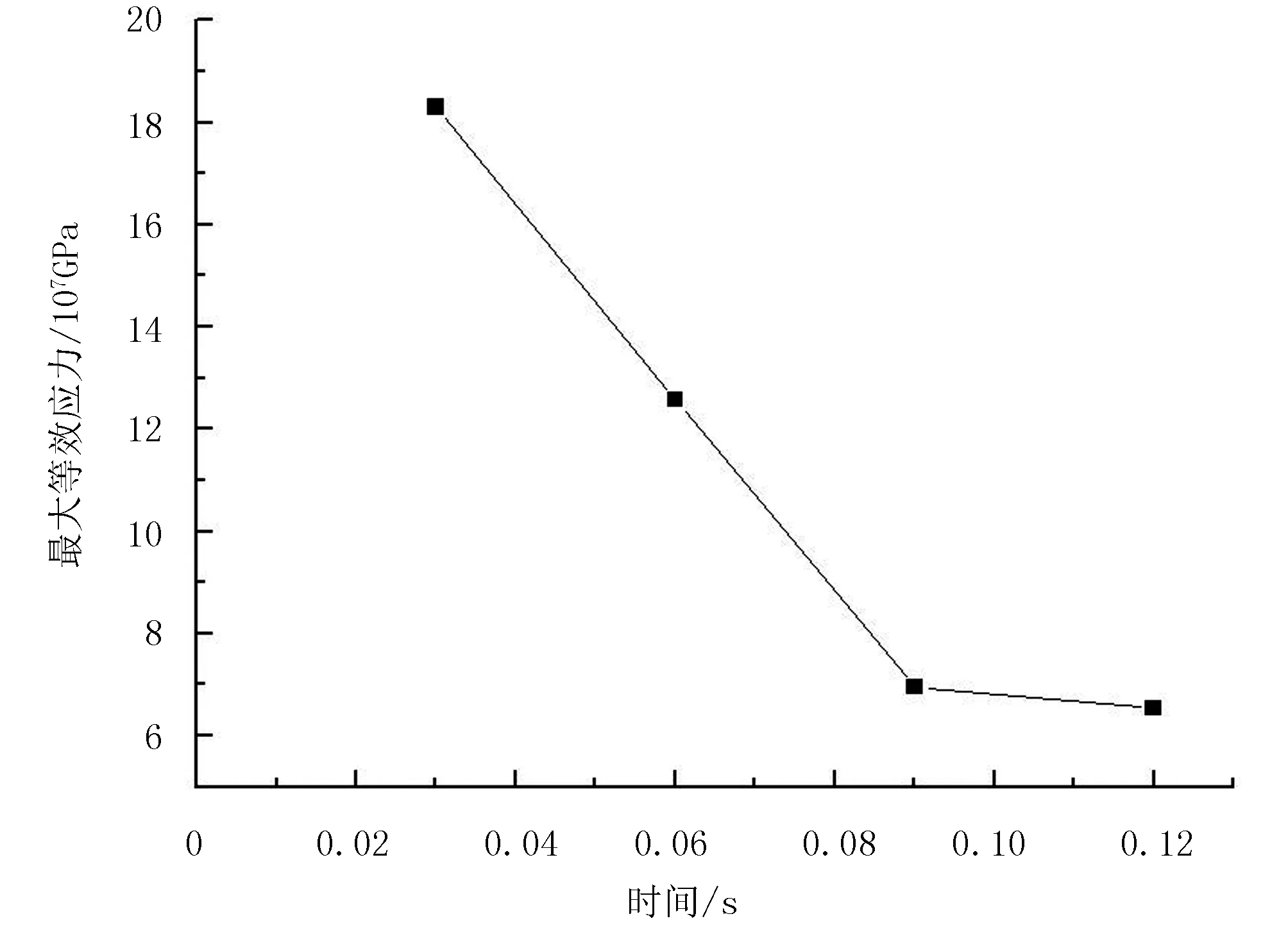
图8 等效应力随时间变化曲线Fig.8 Equivalent stress versus time curve
依照等效应力随时间变化曲线图可以分析出刀具上该单元或者周边单元切削还未切的土壤时的应力数值。分析刀具切削土壤的受力情况,为刀具参数的选取以及优化提供了参考依据。
在土壤模型上选取A(H31384)、B(31385)、C(30013)单元如图9所示。在整个作业过程中,A、B、C3个单元Y方向(即深耕的深度方向)位移由小变大的变化情况如图10所示。
在土壤模型中取点A、B、C单元,由图10观察到它们的Y向位移。在约0.09s时,A单元土壤的Y向(即深耕的深度方向)位移约为0.25m,说明本文设计的深耕机可以达到耕深25cm的深度。

图9 ABC 3个单元Fig.9 Three-units of the ABC
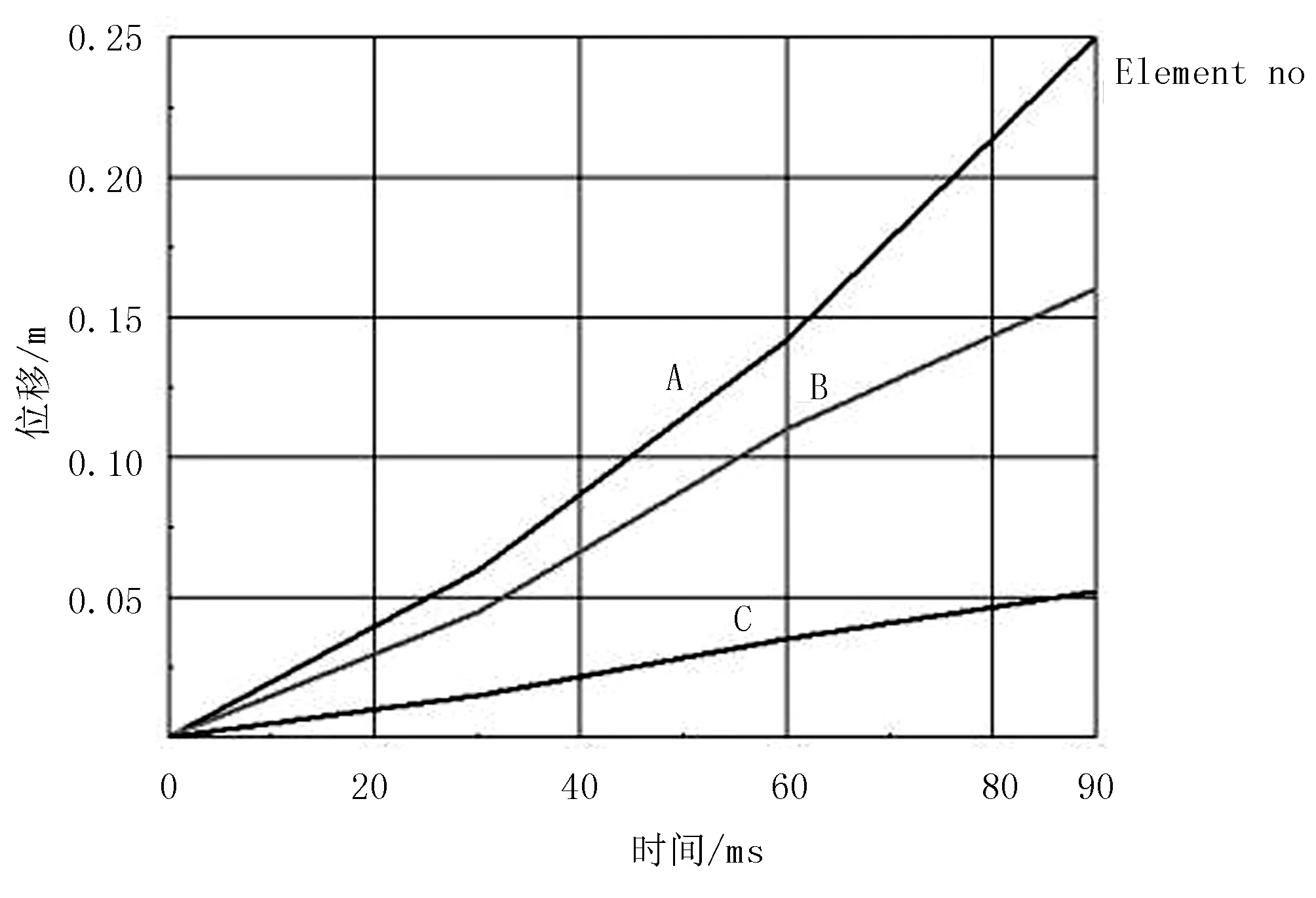
图10 ABC 3单元Y向位移变化Fig.10 The Y-direction displacement of the three-units of the ABC
4 结论
应用有限元分析理论,应用SolidWorks建立刀具模型,导进ANSYS/LS-DYNA软件中,再创建土壤的几何模型;然后运用软件对单个刀具切削土壤过程进行分析,旨在揭示单个刀具-土壤的工作机理。同时,对其切削力以及切削深度进行了分析,验证了所研制出的深耕机可以达到25cm的设计耕深要求,同时也在分析切削力及拟为深耕机刀具与土壤相互作用的数值模拟方面的研究提供了参考。
