我国农业机械化作业水平的组合预测模型对比研究

2019-12-21李鹏飞吕恩利陆华忠陈明林

农机化研究 2019年3期

李鹏飞，吕恩利，陆华忠，陈明林，荀露

(华南农业大学工程学院/南方农业机械与装备关键技术教育部重点实验室，广州 510642)

0 引言

农业机械化是影响我国农业现代化进程、制约农业国际竞争力提高的主要因素[1]，农业机械化作业水平是衡量农业机械化发展水平的重要指标。因此，科学有效地分析我国农业机械化的发展趋势，精准预测农业机械化作业水平的增长幅度，是合理制定农机规划的基础，对于保障我国农业机械化稳定有序的发展具有重要的现实意义。

目前，国内外已提出的关于农业机械化作业水平的预测方法主要有回归分析法、指数平滑法、平滑移动法、灰色模型法，以及人工神经网络等[2-4]。单项预测模型虽各有优势但均有特定的适用环境，仅利用某一种预测模型，预测结果往往偏差较大。综合考虑各单项模型预测时的局限性，Bates和Granger[5]首次提出组合预测的方法，鉴于单项预测方法各自的特点，将不同单项预测方法进行加权组合，使最终预测结果能够包含各单项预测方法中有效的信息，具有很强的适应性和较好的稳定性[6]。

组合预测模型的权重分配对预测精度有重要的影响，合理地确定权重是构建组合预测模型的关键。误差平方和最小法是一种传统的线性加权的方法，以整体最优为目标，在实际中有广泛的应用；Shapley法是一种基于博弈理论中利益分配机制的赋权方法，以公平性为原则，对各单项预测模型进行权重分配；IOWGA法是一种通过诱导值将决策结果进行算数加权集成的方法。目前，尚未发现有关上述3种组合预测模型对比的相关研究。因此，本文以我国农业机械化作业水平时间序列为研究对象，基于提高预测精度的目的，建立了指数曲线预测模型、三次指数平滑模型和灰色预测模型，综合利用各单项模型所提供的有效信息，以误差平方和最小法、Shapley法和IOWGA法建立组合预测模型，通过评价指标比较各组合预测模型的预测效果和稳定性，探讨我国农业机械化作业水平较优的组合预测方法，以期为我国农业机械化发展规划提供科学依据。

1 组合模型的构建

组合预测方法是指选取合理的权重并将多种单项模型的预测结果进行加权组合的方法[7-8]，可以综合各单项模型具有的信息，集成并优化各单项模型的预测结果，使得预测精度大大提高[9]。

1.1 误差平方和最小法[10]

设J表示组合预测相对误差平方和，即

由此可得到以相对误差平方和最小为准则的组合预测模型，即

该模型可转化为矩阵形式，作为非线性规划问题，并且是二次凸规划问题，具有唯一最优解[11]。

1.2 Shapley法[12]

Shapley法[13]是Shapley教授从有效性公理、对称性公理和可加性公理出发，提出的合作对策解的概念[14]，通过团队中各成员的贡献程度反映各成员的重要性[15]，实现总利润在团队中各成员间的公平分配。将各单项预测模型视为合作关系，把组合预测产生的总误差视为合作的总收益，通过Shapley值实现总收益的公平分配，利用分配的结果来确定各单项预测方法在组合预测模型中的权重[16]。

设单项预测方法共有n种，记为I=1，2，…,n；s代表集合I中的任何子集；Es为该子集组合的误差；Ei表示第i种单项预测方法相对误差绝对值的平均值；E表示组合预测方法的总误差，即

其中，t为观测样本个数；eij为第i种单项预测方法第j个数据的相对误差。

Shapley值和权重分配公式分别为

其中，s为集合I中的任何子集；s为单项预测模型的数量；ω|s|为权重因子；s-i为组合中除去第i种单项预测模型。

第i种单项预测模型的权重计算公式为

因此，Shapley组合预测模型为

1.3 IOWGA法

目前，在大多数的组合预测模型中，一般通过各种方法计算出组合预测模型中各单项的权系数，并在预测阶段，假定权系数不变[17-20]。然而，各单项预测方法对同一预测对象的预测效果往往随时间而改变，固定权系数组合不能较好地反映各单项预测模型的时变性。针对上述问题，美国学者Yager[21]提出有序加权平均OWA的概念，即权重分配由各单项预测模型在不同时刻的预测精度决定，克服了传统加权方法的弊端[22]。随着相关理论研究的不断深入，陈华友等[23]提出了诱导有序加权几何平均(IOWGA)的概念，使得权重分配更加合理，组合模型预测精度进一步提高。

定义1：设R+为正实数集，OWGAW：R+n→R+为n元函数，W=ω1,ω2,…,ωmT是与OWGAW有关联的指数加权向量，令

由定义1可知：权系数ωi与序列x1,x2,…,xm中数xi无关，而是与序列x1,x2,…,xm按从大到小进行排序后的第i个位置数bi密切相关。

定义2：设〈a1,x1〉,〈a2,x2〉,…,〈am,xm〉为m个二维数组，令

IOWGAW〈a1,x1〉,〈a2,x2〉,…,〈am,xm〉=

其中，a-indexi为a1,a2,…,am中从大到小的顺序排列的第i个大的数的下标。

称函数IOWGAW是由a1,a2,…,am所产生的n维诱导有序加权集合平均算子，简记为IOWGA，ai成为xi的诱导值。

定义3：表明权系数ωi与序列x1,x2,…,xm中数xi的大小和位置无关，而是与其诱导值按从大到小进行排序后的第i个位置有关。

i=1,2,…,m；t=1,2,…,N

其中，pit为第i种单项预测方法在第t时刻的预测精度，pit∈0,1。与预测值xit对应的预测精度pit视为其诱导值，则m种单项预测方法在第t时刻的预测精度和其对应样本区间的预测值就构成了m个二维数组，即

〈pit,x1t〉,〈p2t,x2t〉,…,〈pmt,xmt〉。

设L=l1,l2,…,lmT为单项预测方法在组合预测中的OWGA的加权向量，将m种单项预测方法在t时刻的预测精度序列p1t,p2t,…,pmt按从大到小的顺序进行排列，设p-indexi是第i个大的预测精度的下标，令

IOWGAL〈p1t,x1t〉,〈p2t,x2t〉,…,〈pmt,xtm〉=

i=1,2,…,m；t=1,2,…,N

由上式可知：IOWGA组合模型将各单项模型在不同时刻的预测精度作为诱导值进行赋权，使得单项模型各时刻的权重与其该时刻的拟合精度相关联，更具有实际意义。

为了简化计算，将取对数误差平方和作为优化准则，令ea-indexit=lnxt-lnxp-indexit。

N期总的组合预测对数误差平方和S为

基于对数误差平方和最小的准则，IOWGA算子组合预测模型为

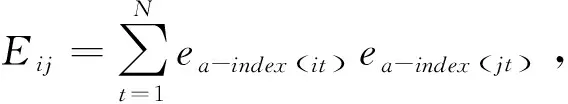
minSL=LTEL

2 算例分析

2.1 数据来源

本文采用的是2000-2015年我国农业机械化作业水平的年度数据，数据来源于《中国农业机械化年鉴》，如表1所示。各单项预测模型均以2001-2012年的数据作为训练样本，对2013-2015年的数据进行预测检验。

2.2 评价指标

为了对组合预测模型给予有效的评价，本文采用平均相对误差MAPE和均方根误差RMSE为评价指标。则

2.3 单项预测模型的建立

我国农业机械化作业水平是一个时间序列，其数值的变化具有波动性，以增长为主要趋势。选择指数曲线法、三次指数平滑法和灰色预测法建立我国农业机械化作业水平单项预测模型。

2.3.1 指数曲线模型

由于社会的进步与科技的发展，我国农业机械化作业水平随着时间的推移呈现明显的快速增长趋势。由表1可知：我国农业机械化作业水平与时间近似满足指数关系，通过SPSS软件对2001-2012年的历史数据进行指数曲线拟合，得到预测模型如下，相关系数R为0.955，表明我国农业机械化作业水平与时间具有较强的相关性，即

y=2.788×10-47e0.053x

其中，x为时间变量；y为对应年份的农业机械化作业水平预测值。

2.3.2 三次指数平滑模型[24]

指数平滑预测法可细分为一次、二次、三次指数平滑预测法，综合考虑历史数据的变化趋势，本文采用三次指数平滑法。

设原始数据所组成的时间序列为X=x1,x2,…,xn，则三次指数平滑模型为

yt+T=at+bt·T+ct·T2

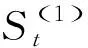
平滑系数的计算公式为

其中，α代表模型对时序变化的反应速度[25]。本文经反复测算和比较后，综合考虑评价指标，选取α=0.8。

本文建模数据量较小，初始值对预测效果影响较大，所以采用平均数法求平滑初始值，即

将2001-2012年，农业机械化作业水平历史数据代入，求得at、bt、ct的值及2001-2012的预测值。此外，令t=2012，得到公式如下，求得2013-2015年的预测值如表1所示。

y2012+T=0.5717+0.0218T-0.0016T2

2.3.3 灰色模型[26]

灰色预测是对原始序列发展变化进行深入探索，生成有较强规律性的数据序列，建立微分方程模型，预测时序未来发展趋势[27]。灰色模型适用于样本量较少情况下的时序预测。

设原始灰色时间序列为x0，则

x0=x01,x02,…,x0n

对其进行一次累加得到新序列x1，即

对新序列x1建立白化微分方程，得

其中，a、b为待估计参数；t为时间。

求解上式得到时间响应模型为

i=1,2,…,n-1

按最小二乘法求解参数a和b，则有

由此得到模型还原值为

i=1,2,…,n

将2001-2012年农业机械化作业水平历史数据代入上述预测模型，求解待估计参数a、b，得到灰色预测模型为

i=1,2,…,n-1

通过上式对2013-2015年我国农业机械化作业水平进行拟合，并得到还原值，结果如表1所示。

表1 3种单项模型的预测结果

2.4 组合预测模型的建立

2.4.1 误差平方和最小模型

通过MatLab平台计算得到基于误差平方和最小的组合预测模型为

2.4.2Shapley模型

根据Shapley概念，参与组合预测模型总误差分配的成员为I=1,2,3，它所有子集的组合误差分别为E1、E2、E3、E1,2、E1,3、E2,3、E1,2,3。

求得各成员的Shapley值，并计算各单项预测模型的权重，Shapley值组合预测模型为

2.4.3 IWOGA模型

按照表1中的预测结果，计算出各单项模型在各时刻所对应的预测精度，并视为诱导值，利用MatLab解得最优权系数为l1=0.6352，l2=0.3648，l3=0。

其中，l1、l2、l3为3个单项模型预测精度从高到低的单项模型赋权重。

根据表1的数据，通过预测连贯性的原则，即各个单项预测模型在未来的第N+T年的预测精度与其过去的T年内的平均预测精度保持一致[28]，推测出各单项预测模型2013-2015年可能的预测精度状态，从高到低进行排序，排序结果如表2所示。

表2 2013-2015年各单项模型预测精度的排序结果

2.5 结果与分析

误差平方和最小、Shapley、IWOGA3种组合预测模型对2013-2015年农业机械化作业水平进行预测，预测结果如表3所示。

由表3可以看出：组合预测模型对我国农业机械化作业水平的总体预测精度较高，观测值与预测值吻合性较好，相对误差均在3%范围内。IOWGA组合模型的预测精度较高，平均相对误差仅为0.003 9，误差平方和最小模型次之，Shapley模型的预测性能较低。通过均方根误差的结果可知，IOWGA组合预测模型不仅误差较小，误差分布也较集中。