基于广义统一概率图的东南沿海风速概率分布研究

林立　陈政清　洪华生　华旭刚　夏丹丹　王淮峰　胡海涛

摘   要：传统的概率分布选择方法是基于观测数据在假设分布概率纸上进行绘制，由于受到概率纸的限制无法进行直接比对分析. 本文提出了一种新的广义统一概率图（GUPP）方法，通过Rosenblatt变换，将假设分布转换到统一概率纸上进行直观比对，并提出基于GUPP的拟合优度快速检验方法及参数，该方法可用于大数据量和大范围假设概率分布的快速拟合和检验. 采用本文方法对厦门地区1953-2015年采集的实时风速数据进行统计分析及拟合，结果显示Pearson-Ⅲ分布可以更好地模拟厦门地区年10 min平均最大风速的分布规律，以此更准确地确定厦门地区基于不同回归期的设计最大风速.

关键词：广义统一概率图法;年10 min平均最大风速;拟合优度检验;分布函数

中图分类号：P425                                  文献标志码：A

Analysis of Wind Speed Distribution Probability in Southeastern Coastal

of China Based on Generalized Unified Probability Plot

LIN Li1，2，CHEN Zhengqing1，HONG Huasheng3，HUA Xugang1，

XIA Dandan2，WANG Huaifeng2，HU Haitao2

（1. College of Civil Engineering，Hunan University，Changsha 410082，China;

2. Hercynian Wind Engineering Research Center，Xiamen University of Technology，Xiamen 361024，China;

3. Department of Civil & Environmental Engineering，University of California，Irvine，CA 92697，USA）

Abstract： The traditional probability distribution selection method is based on the observation data and plotted on the probability paper of a hypothetical distribution， which cannot conduct the direct comparison analysis due to the limitation of the probability paper. In this paper， a new generalized unified probability plot （GUPP） method is proposed. Through the Rosenblatt transform， the hypothesis distribution is transformed into a unified probability paper for visual comparison， and an efficient test method and comparison parameters are proposed based on GUPP which can be used for quick fitting and testing of large data volumes and large-scale hypothetical probability distributions. In this research， the proposed method is also used to statistically analyze and fit the real-time wind speed data collected in Xiamen from 1953 to 2015. The results show that the Pearson-Ⅲ distribution is better for annual average maximum 10-minute wind speed in Xiamen and for determining the maximum wind speed for structural design in Xiamen from different regression periods.

Key words： generalized unified probability plot（GUPP）;annual average maximum 10-minute wind speed;fitness test;distribution function

中國东南沿海地区受台风等强风天气影响明显，近年来基础建设高速发展，许多风敏感结构如高层建筑、大跨结构等在该地区相继建起，如何选择设计风速是该地区抗风设计中面临的基本问题[1-2]. 在《建筑结构荷载规范》中，推荐Gumble分布为年度最大10 min平均风速的分布函数，用于东南沿海地区的结构风荷载设计[3-5]，但是，一些特殊区域，如离岛型城市厦门，其最优的分布规律应进行区别性的分析，以适应该区域独特的强风环境和更高的抗风设计要求[6-8].本文分析了1953年至2015年记录的原始风速数据，以此为基础确定当地年最大10 min平均风速的最优概率分布;为更高效快速地进行最优分布筛选，建立了广义统一概率图法（GUPP），并引入距离参数来定量指示不同分布的拟合优度. GUPP方法有效地从众多假设分布中快速获取最优分布作为厦门地区年10 min平均风速的最佳拟合分布，并根据设计回归期需要从中得到该地区合理的设计风速参数.

1   年最大风速分析

1.1   基本风数据分析

厦门市气象数据服务中心记录的厦门市1953年到2015年的原始气象数据，分为2个阶段. 第1阶段从1953年到2004年每天记录4次平均2 min风速，第2阶段从2005年到2015年记录的平均10 min风速. 第1阶段数据采用一天4次2 min平均风速的记录方法，可能会错过最强风纪录，目前我国《建筑结构设计荷载规范》统一采用10 min平均风速. 因此，在本研究中，将2 min平均风速记录数据统一换算为10 min平均风速[9]：

其中：V2-min为原始2 min平均风速， V10-min为10 min平均风速. 结合2个阶段的实测数据，可得63年的平均10 min最大风速，如图1所示.

根据转换修正后的厦门市1953-2015年平均10 min最大风速，计算年最大风速参数，如表1所示，其经验累积分布函数和概率分布函数直方图分别如图2、图3所示.

1.2   传统概率绘图法

传统的选择最优概率分布的方法是基于一组观测数据绘制的概率紙法，在具有不同散点和参考线的各类概率纸上表现，可以较为直接地验证假设分布，根据参考直线和散点之间的距离来检验拟合优度，评估假设分布的拟合程度，如图4、图5所示. 由于概率纸型式有限，不同概率纸差别较大，假设分布之间无法进行直观的比对，传统概率纸法的使用将受到制约.

1.3   广义统一概率图

本研究提出了一种更有效地绘制分析数据的新方法，即广义统一概率图法（GUPP）.  假设随机变量X和Y分别遵循分布函数FX（xi）和ψY（yi），根据Rosenblatt变换，当分布FX（xi）等于分布ψY（yi）时，相应随机变量X可以转换为随机变量Y，如式（2）：

以ψ（·）为参考分布函数，GUPP方法可在同一概率纸中绘制不同假设分布样本数据，以进行直观比对，计算绘制过程如下：

1）绘制概率图坐标. 假设随机变量X和Y分别服从分布F（xi）和ψ（yi），根据Rosenblatt变换原理，当FX（xi） = ψY（yi）时，yi = ψ-1Y（FX（xi））. 其中，xi（i = 1，2，3，…，n）为服从分布函数F（xi）的随机变量X的n个样本，则可以得随机变量Y的n个样本的yi（i = 1，2，3，…，n），X是否服从FX分布等价转化为Y是否服从ψY分布. 在假设累积分布函数曲线FX（·）中选取若干个点（xi，Fi），根据yi = ψ-1Y（FX（xi）），由ψ-1Y（FX（xi））计算出的值作为第i个点在概率图中的横坐标，ψ-1Y（F（i））为与之相对应的概率图的纵坐标.

2）绘制参考曲线. 连接所有（ψ-1Y（FX（xi）），

ψ-1Y（F（i）））点，由于FX（xi）等于F（i），因此ψ-1Y（FX（xi）） = ψ-1Y（F（i）），即任意点的纵坐标和横坐标相等，参考曲线为过原点的对角线.

3）绘制样本可能服从的假设分布的样本点集.

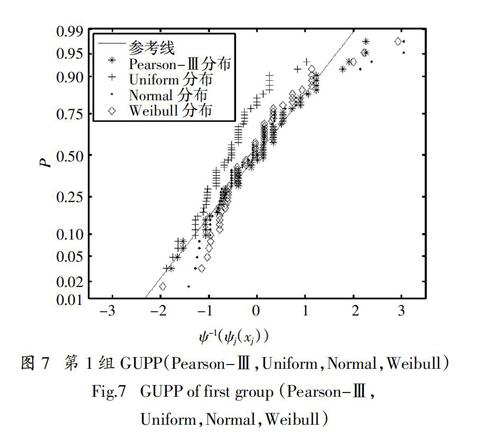
按照升序排列样本xi，X的n个次序统计量x（1）

ψ-1[ψj（xi）]和ψ-1（Pi）分别为样本点所对应的假设分布换算后的样本点集的横坐标和纵坐标. 以此类推，可得到各种假设分布类型ψj（j = 1，2，…，N）的样本点集.

4）将参考线与假设分布的散点进行比较，通过最佳拟合参考线的对应点获得最佳分布. 其他拟合度测试方法也可以用于确定变换后的散点的最优分布函数.

以最常见的统计分布标准正态分布作为参考分布ψ（·），利用GUPP方法绘制不同假设分布下的年平均最大风速，结果如图6所示. 图中，y轴为经百分位数[0.01 0.02 0.05 0.1 0.25 0.5 0.75 0.9 0.95 0.99]转换的经验累积分布的反函数，本文为了助于显示与概率的关系，y轴仍表示为转换前相应的百分位数.

1.4   厦门年最大风速分析

采用GUPP方法分析厦门年平均10 min最大风速. 图2和图3 分别为厦门最大年风速的CDF和PDF图，利用12个分布函数分析厦门的风速分布，采用GUPP方法比较不同分布. 根据数据样本，本研究选择12个分布作为假设分布：Gamma、Inverse Gaussian、Gumbel、Uniform、Normal、Weibull、Rician、Log-normal、Logistic、Log-logistic、Pearson-I和Pearson-Ⅲ. 其概率密度函数如表2所示.

式（2）中的ψY（y）如果选择为标准正态分布ΦY（y），式（2）可以转换为如下：

式中：yi为标准正态分布变量的随机样本.

为了便于直观识别，将所有12个分布随机分成3组，使用数值分析软件MATLAB拟合分析，利用最大似然估计得出各分布参数，其标准正态概率图相应的GUPP如图7～图9所示. 其中，y轴为实际累积经验分布函数经过转换后的累积概率分布. 同时，x轴是从假设分布的累积分布转换的标准正态累积分布函数的参数.

由图7可知，Pearson-Ⅲ分布表现出比Uniform、Normal和Weibull更好的拟合度. 图8中，Gumbel 比Rician、Log-logistic、Inverse Gaussian分布能更好地拟合风速. 图9中，Gamma，Pearson-I，Log-normal和 Logistic分布都能很好地拟合风速分布，在高风速区域，Pearson-I能更好地拟合风速. 为能更准确地比较风速拟合度，将3组中拟合度较好的Pearson-Ⅲ，Gumbel及Pearson-I分布进行比较，结果如图10所示. 比较结果显示，在广义概率分布图中，Pearson-Ⅲ及Pearson-I拟合厦门地区年平均10 min最大风速结果均明显优于Gumbel分布. 在高风速区Pearson-Ⅲ和Pearson-I拟合程度差别不大，而在低风速区Pearson-Ⅲ分布拟合与参考线吻合性较好. 因此，在GUPP的初步筛选中，暂选Pearson-Ⅲ分布作为厦门地区平均10 min最大风速的推荐分布. 进一步的判断，通过后继的拟合优度检验方法来进行确定.

2   拟合优度检验

拟合优度检验是定量判别分布拟合程度的重要定量参数，目前Kolmogorov-Smirnov （K-S）[10-11]检验等方法由于数学意义明确等优点被广泛采用，其统计量定义如下：

式中：Fn（x）为待检验数据的经验分布;F0（x）为理论分布的分布函数;Dn为二者差距的最大值. K-S检验首先建立假设检验，基于样本数据计算经验分布函数与理论分布函数计算Dn，查表确定置信区间内的临界值Dn（a），若Dn > Dn（a），即拒绝假设，计算过程较复杂，在快速判别方面没有优势. 广义统一概率图中，拟合度检验可以直接从检验假设分布F（xi）的随机变量的拟合度转换为测试参考分布ψ（·）的变换后数据的拟合度. 基于GUPP方法，本文提出了 “距离参数D”用来快速初步检验分布拟合度. 基于Rosenblatt变换后的概率图模型，该参数被定义为均方根（RMS）值或变换后的散点与参考线之间的垂直距离的期望值.  参考线的方程式如公式（5）：

离参数的均方根为：

竖向距离参数的期望值为：

式中：FX（xi）是第i个按递增顺序重新排列x的实际经验累积分布函数，N是样本数. 距离参数不是统计检验，而是基于数据的平均距离参数直观地测量假设分布的拟合度. 众所周知，当分布具有更好的拟合度时，K-S的P值应该更高，而更优的分布应导致距离参数值更小. 为了有效地比较这两种类型的检验，K-S检验的P值采用Pr如式（8）：

其中P為K-S检验值. 为确保基于GUPP的检验方法有效，计算使用原始数据的K-S检验结果和基于GUPP的距离参数检验结果，二者检验结果相同，因而证明了GUPP的拟合优度检验结果的有效性. K-S检验和基于GUPP方法的距离参数检验结果见表3. 表 3   拟合度检验结果

图11为不同假设分布的K-S检验及距离参数检验对比. 由图11可知，Pearson-Ⅲ分布的拟合结果最优，因此，厦门地区的年最大风速分布函数和Pearson-Ⅲ分布最为吻合，如式（9）（10）所示：

式中：a = 10α4 - 12α3 - 18 = 11.876 8;b = α3（α4 + 3） = 9.102 2;c = 4α4 - 3α3 = 13.338 4;d = 0;K取决于

Fx（+∞） = 1，本研究 K = 0.084.

工程结构抗风设计中，设计年最大风速取决于设计期望的回归期. 对于厦门地区，结构设计风速可以通过Pearson-Ⅲ分布及其指定T年回归期准确地确定. Pearson-Ⅲ和规范推荐的Gumbel的GUPP、CDF、PDF比对如图12～14所示. 为了进一步研究两种分布的差异，继续讨论基于不同回归期的风速风压取值.

3   不同回归期的风速风压取值分析

根据中国载荷规范，确定结构风荷载有两种方法，一种是基于Gumbel风速分布，另一种是由该地区的基本风压直接计算出来. 以对风荷载敏感的高层建筑为例，对现有规范规定的Gumbel分布及本文根据当地风速历史记录拟合得到的Pearson-Ⅲ分布下的厦门市建筑风压进行比较. 根据《建筑结构荷载规范》和《福建省建筑结构风压规程》[3，12]，结构性能设计的基本风压回归期为100年，水平位移估算的回归期为50年，150 m以上建筑物设计中舒适度要求回归期为10年.

表4为厦门地区风速和由Pearson-Ⅲ分布确定的风压，以及基于Gumbel分布确定的风压. Gumbel分布和基本风压均由中国载荷规范和福建风规程推荐，回归期为T=10、50和100年. 比较Pearson-Ⅲ与Gumbel分布，在较低的风速下（如T=10年），基于Pearson-Ⅲ分布计算的风压比Gumbel的风压小9%，但对于高风速（T>50年），Pearson-Ⅲ分布的风压比Gumbel高出约19%. 对于更长的回归期，由于没有历史风速数据记录，因此根据Gumbel分布的估算不可靠，仅能确定基本风压. 如图15，Pearson-Ⅲ分布确定的风压比本规范规定的基本风压低约15%至25%.

4   结   论

本研究对厦门地区1953年至2015年间记录的平均风速数据进行了详细分析，提出了更加高效的广义统一概率图（GUPP）方法，对12个假设概率分布进行了检验，以确定厦门市年平均10 min最大风速的最优分布，得到以下结论：

1）提出的GUPP方法可以有效地用于区域风速的最佳拟合分布，通过引入距离参数，可以快速地定量判别不同概率分布的拟合度;

2）根据当地历史风速数据记录分析，Pearson-III分布更适合作为厦门地区年最大10 min平均风速概率分布模型;

3）基于Pearson-Ⅲ分布，可以更准确地确定厦门地区不同回归期的设计最大风速;

4）当本地数据可用时，应采用更符合当地实际的概率分布来确定不同回归期的风速，这有利于优化建筑物和结构的抗风设计参数的精确取值.

参考文献

[1]    柯世堂，王浩. 超高层连体建筑风荷载干扰效应大涡模拟研究[J].湖南大学学报（自然科学版），2017，44（5）：53—62.

KE S T，WANG H. Large eddy simulation investigation of wind loads and interference effects on ultra high-rise connecting building[J]. Journal of Hunan University（Nature Sciences），2017，44（5）： 53—62. （In Chinese）

[2]    何旭辉，秦红禧，邹云峰，等. 台风外围影响下的大跨度拱桥桥址区近地风特性实测研究[J]. 湖南大学学报（自然科学版），2017，44（1）：23—31.

HE X H，QIN H X，ZOU Y F，et al. Field measurement and investigation of wind characteristics at the site of a long-span arch bridge in the periphery of typhoon kujira [J]. Journal of Hunan University （Nature Sciences），2017，44（1）：23—31. （In Chinese）

[3]    中华人民共和国住房和城乡建设部.建筑结构荷载规范[S].北京：中国建筑工业出版社，2012：165—168.

Ministry of housing and urban-rural development of the People's Republic of China. Building structure load specification[S]. Beijing：Press of Chinese Building Industry，2012：165—168. （In Chinese）

[4]    吴红华，米慧敏. 非高斯脉动风压的分形模拟研究[J].湖南大学学报（自然科学版），2017，44（7）：59—68.

WU H H，MI H M. Research on fractal simulation of non-gaussian fluctuating wind pressure [J]. Journal of Hunan University （Nature Sciences），2017，44（7）：59—68.（In Chinese）

[5]    庞佳斌.沿海和山区强风特性的观测分析与风洞模拟技术研究[D]. 上海：同济大学土木工程学院，2006：30—43.

PANG J B. Observational analysis and wind tunnel simulation technology of strong wind characteristics in coastal and mountainous areas[D]. Shanghai： Department of Civil Engineering，Tongji University，2006：30—43. （In Chinese）

[6]    庞文保，白光弼，滕跃，等. P-Ⅲ型和极值I型分布曲线在最大风速计算中的应用[J].气象科技，2009，37（2）： 221—223.

PANG W B，BAI H B，TENG Y，et al. Application of P-Ⅲ type and extreme value I distribution curve in calculation of maximum wind speed [J]. Meteorological Technology，2009，37（2）：221—223.（In Chinese）

[7]    LEI Y，TAO L，ZHANG G，et al. Numerical simulation of the characteristics of typhoon wind-field in Xiamen region[J]. Engineering Mechanics，2014，31（1）： 122—128.

[8]    董安正.高层建筑结构抗风可靠性分析[D].大连：大连理工大学土木工程学院，2002：43—60.

DONG A Z. Wind-resistant reliability analysis of tall building structures[D].Dalian： Department of Civil Engineering，Dalian University of Technology，2002： 43—60. （In Chinese）

[9]    荷載规范修订组. 荷载规范中的基本风压问题[J].建筑结构，1976（5）：30—40.

Load specification revision group. Basic wind pressure problems in load specifications[J]. Building Construction，1976（5）：30—40.（In Chinese）

[10]  STEPHENS M A. EDF statistics for goodness of fit and some comparisons[J]. Journal of the American Statistical Association，1974，69（347）： 730—737.

[11]  XIAO Y，LI Q，LI Z. Probability distributions of extreme wind speed and its occurrence interval [J]. Engineering Structures，2006，28（8）：1173—1181.

[12]  福建省住房和城乡建设厅. 福建省建筑结构风压规程[S].福州： 福建省住房和城乡建设厅，2011：4—6.

Fujian provincial department of housing and urban-rural development. Fujian wind pressure regulations for building structures [S]. Fuzhou： Fujian Provincial Department of Housing and Urban-Rural Development，2011：4—6. （In Chinese）