多胞鞋底结构性能分析及胞元参数影响
2019-12-20凌静秀杨晓静吴志鸿2詹友基
凌静秀,2,杨晓静,吴志鸿2,詹友基
(1.福建工程学院 机械与汽车工程学院, 福建 福州 350118;2.中建海峡建设发展有限公司,福建 福州 350000)
多胞结构作为一种超轻多功能结构,具备相对密度低、质量轻、缓冲性能好等诸多优点,广泛应用于汽车、航天、航空等领域,将多胞结构应用于运动鞋底能够使其具有良好的缓冲、助力特性。我国已成为世界上最大的鞋类生产和出口国,这种高份额比例主要集中在中低端鞋业,在高级鞋类市场,尤其是高端运动鞋,国内外品牌还存在一定差距。国外运动鞋品牌厂商提出的蜂窝科技技术,在运动鞋的减振技术上得到成功应用。国内厂商同样提出类似的动力巢鞋底,结构、形状与国外品牌相似,但各项性能指标低于国外同类产品。由于技术封锁等原因,国外关于鞋底多胞结构性能分析的参考资料很少。而我国厂商通过引进吸收国外技术,参考鞋底结构形状进行仿制,关键技术及性能始终无法突破。因此,有必要在传统鞋底结构方案的基础上,构造多胞鞋底方案,分析不同工况下鞋底结构的动静性能,进而为运动鞋底的结构设计提供技术指导。
关于运动鞋底及多胞结构的研究,国内外学者发表了诸多学术成果。汤运启等[1]采用鞋垫足底压力测试和冲击减振测试方法对运动鞋减振性能进行研究,提出了运动鞋底减振性能评价的可信指标。刘丽[2]同样采用鞋垫足底压力技术,结合表面肌电技术,对不同结构的运动鞋减振性能进行分析,实现了“人足合一”的设计理念。徐文泉等[3]使用ANSYS/LS-DYNA模块对运动鞋的减振和止滑性能进行数值模拟,得到不同载荷条件下鞋底的最大冲击力、最大变形量等指标,为其减振和止滑性能评价提供有效支撑。李响等[4]通过优化六边形和四边形夹心胞元,提出了一种新的多胞结构,并以蜂窝夹层板为例,对其进行数值模拟,验证了结构的合理性。赵显伟[5]对比分析了3种不同的蜂窝结构,验证了蜂窝结构可满足飞机面内低模量和面外高承载要求,为蜂窝结构在航天领域的应用作出了贡献。何斌、李响[6]设计了一种由菱形和圆形组成的新型蜂窝结构,并用有限元法对其稳定性进行分析,得出该种蜂窝结构轴向承载力强,是一种综合性能较强的创新力学结构,对蜂窝结构在抗压、减振等方面的应用具有一定的借鉴。方廷[7]依据人体工程学理论,分析研究了人体足部健康与在运动中足底所受压力的关系,提出减振性能和止滑性能是鞋底设计中需要重点关注的指标。王海涛[8]基于工程仿生学原理,将鸵鸟足垫应用在运动鞋鞋底中底结构设计上,提出了一种新型的具有优良减振性能和缓冲效果的运动鞋中底。Galehdari等[9]结合理论推导、数值及实验分析了分层蜂窝结构在低速、准静态加载情况下的平面应力。Holloman等[10]对可压缩方形蜂窝结构的冲击特性进行了仿真和实验,对比分析不同参数下的性能。Wang等[11]对在冲击和振动情况下的蜂窝结构力学特性进行了分析,结论可应用于表征和提高蜂窝结构的压缩性能。
综上所述,在多胞结构特性及设计方面,国内外主要采用理论推导、数值仿真和实验等手段,研究多胞结构在不同应用领域的力学性能、结构性能及胞元设计方法等问题。而多胞结构应用于鞋底系统的相关资料还鲜有报道,对运动鞋的性能分析也主要集中在鞋底减振性能及止滑性能等方面,以及刚度、碰撞力监测等指标[12-13]。本文结合国内外现有的研究资料,将多胞结构技术运用到运动鞋的结构设计上,并对多胞鞋底结构进行静力学特性及尺寸参数影响分析,为不同工况下运动鞋底设计提供理论方法及技术支撑。
1 运动鞋鞋底模型结构设计
一般的运动鞋鞋底是由大底、中底、内底3部分组成。大底是与地面接触的部分,中底夹在大底和内底之间,内底的顶部直接与脚底接触。大底主要起止滑、耐磨作用,中底具有减振、缓冲功效,内底主要用于支撑脚面和分散足底压力。
1.1 大底造型设计
一般大底的厚度设计要求运动鞋在使用寿命期限内能抵抗足够的磨损,不影响受弯部位的弯曲,保证运动者的活动不受大底厚度影响,同时脚体无明显不适,还能减少运动者的体能消耗。大底的厚度因运动而异,一般运动鞋的厚度在鞋底前掌部位10 mm左右,后跟部位32 mm左右。本文参考42码运动鞋的鞋底,设计大底前掌部位厚度3 mm,后跟部位厚度10 mm,长度260 mm,大底前掌最宽处93 mm,后跟最宽处70 mm,内外侧厚度差3 mm,大底斜面斜度60°。设计普通运动鞋底结构的大底模型如图1所示。

图1 大底结构模型Fig.1 Structural model of outsole
1.2 中底造型设计
中底厚度的设计与鞋底总厚度有关,往往取决于中底功能设计要求。由于具有减振作用的多胞结构是排列在中底上,所以中底的设计需要留有足够的厚度。本文设计中底的前掌部位厚度为5 mm,后跟部位厚度为15 mm。设计的中底结构模型如图2所示。

图2 中底结构模型Fig.2 Structural model of insole
1.3 内底造型设计
内底设计考虑以下几个因素:内底材料和结构、内底硬度、内底厚度、内底形状、内底和中底的组合。本文设计的内底结构数据为:长度占足长的105%。设计时以内底样为基础,前端合拢至35 mm,脚趾头两侧合拢至2 mm,从内腰窝释放2.5 mm,从外腰窝释放1 mm,鞋跟周边释放1.5 mm。内底的厚度数据为前掌部位厚度3 mm,后跟部位厚度5 mm。设计的内底结构模型如图3。

图3 内底结构模型Fig.3 Structural model of innersole
1.4 多胞结构设计方案
整个鞋底中起到减振作用的主要是中底结构,为此本文将多胞结构设置在中底上。设计两种胞元结构,即菱形和正六边形的蜂窝结构排列,这两种都是目前市场上典型的减振结构。菱形胞元边长5 mm,角度60°,胞元间距2 mm,在中底底面上均匀分布。菱形凹槽深度2 mm,凹槽斜度为60°。同理,设计正六边形的胞元边长5 mm,角度120°,胞元间距2 mm,凹槽深度2 mm,斜度60°。两种胞元结构的中底结构如图4所示。

图4 多胞结构中底Fig.4 Insole with multi-cell structure
1.5 运动鞋鞋底模型结构
将上述建立的大底、中底及内底结构进行装配,分别得到传统普通运动鞋底和多胞运动鞋底的结构模型如图5所示。

图5 鞋底结构模型Fig.5 Sole structure model
2 运动鞋鞋底静力学性能分析
2.1 典型载荷工况定义
多胞鞋底的载荷工况和正常运动鞋一致,可分为正常行走、匀速奔跑以及跳跃3种工况。本文确定载荷的依据为不同工况下的足底峰值压强和峰值压力。施加载荷分为鞋底的前掌和后跟两部分。通过实际测绘得出前掌面积约60 cm2,后跟面积约50 cm2。
由文献[2]可知,人在裸足的状态下行走时,前掌区域的峰值压力为15 N/cm2,后跟区域的峰值压力为13.5 N/cm2。前后掌的峰值载荷计算如下:
式中,A1为前掌面积;A2为后跟面积;Fa1为前掌区域的峰值载荷;Fa2为后跟区域的峰值载荷;Pa1为前掌区域的峰值压力;Pa2为后跟区域的峰值压力。
同理,在匀速跑步工况时,前后掌区域的峰值压力分别为17.5 N/cm2及15 N/cm2;而在跳跃工况时,前后掌区域的峰值压力分别为29.5 N/cm2及32 N/cm2。同样可根据前后掌承载面积计算出各自的峰值载荷大小。
2.2 静力学性能分析
分别将普通鞋底及多胞鞋底的三维模型导入到有限元分析软件ANSYS Workbench中。首先定义大底材料为橡胶:密度1.3 g/cm3,弹性模量7.8 MPa,泊松比0.47。中底和内底材料为EVA材料:密度0.93 g/cm3,弹性模量1.4 MPa,泊松比0.46。采用绑定接触算法模拟鞋底各部件间的胶粘,并用Hex-dominant方法对模型进行网格划分,得到六面体占优的鞋底混合有限元网格模型如图6所示。

图6 鞋底有限元网格模型Fig.6 Finite element mesh model of sole
按照典型载荷工况对模型进行加载,并约束大底与地面接触的平面,对3种鞋底模型进行静力学分析,对比静力学指标,进而体现多胞鞋底结构的性能优越性。通过分析得到鞋底在不同工况下的变形,其中跳跃工况的变形分布如图7所示。

图7 跳跃工况下鞋底变形分布云图Fig.7 Distributions of sole deformation under jumping condition
将3种鞋底在不同工况下的变形结果导出,计算出鞋底的平均变形量如表1所示。

表1 不同工况下鞋底平均变形量
由以上分析结果可知:
1)菱形和正六边形多胞结构鞋底变形基本是均匀分布的,大部分区域的变形量在鞋底两边,而普通鞋底的变形是从中间逐渐向外扩展,导致鞋底中间凸起和周围凹陷,影响鞋子的舒适性。
2)普通鞋底平均变形量最小,正六边形多胞结构鞋底的平均变形量最大。变形量越大,结构刚度越小,说明鞋底的能量吸收率也越大,从而得出其减振性能越好。由此可知,正六边形多胞结构鞋底的减振缓冲性能在三者中最优越。
3 正六边形多胞鞋底参数影响
3.1 胞元边长尺寸影响
保持正六边形胞元的凹槽深度为2 mm不变,对比现有蜂窝鞋底胞元尺寸,将原方案5 mm的边长分别设计为4 mm和6 mm,重新建模进行静力学分析,得到胞元边长对鞋底性能的影响。
对3种边长的正六边形胞元鞋底结构进行静力学分析,结果如表2所示。
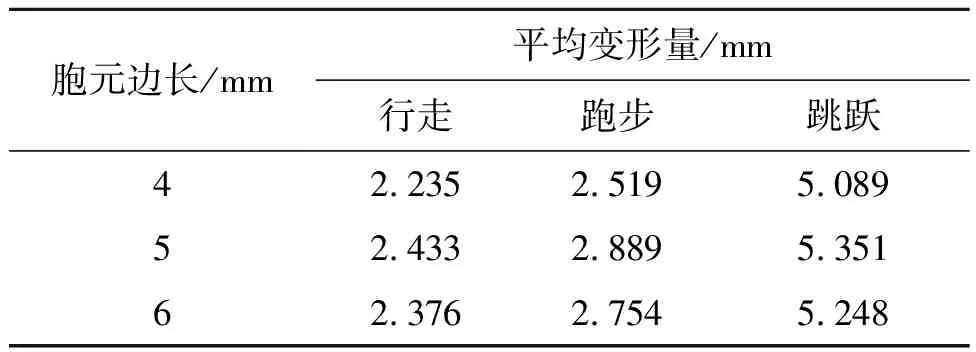
表2 不同胞元边长的鞋底平均变形量
由表2可知,边长5 mm的正六边形多胞鞋底结构的平均变形量最大,即缓冲减振性能最好。
3.2 胞元凹槽深度影响
同理,保持正六边形胞元的边长为5 mm不变,将原方案2 mm的凹槽深度分别设计为1.5 mm和2.5 mm。通过对不同方案的鞋底静力学分析,得到胞元凹槽深度对鞋底性能的影响。3种凹槽深度的正六边形胞元鞋底静力学分析结果如表3所示。

表3 3种不同凹槽深度的鞋底平均变形量
由表3可知,凹槽深度为2.5 mm的正六边形多胞结构鞋底的平均变形量最大,即确定2.5 mm为正六边形凹槽深度的较优尺寸。
4 结论
1)相同载荷工况下,多胞鞋底结构的变形量分布较均匀,且正六边形多胞鞋底的平均变形量最大,缓冲性能最优越。
2)相同工况下,正六边形胞元的凹槽深度保持2 mm不变情况下,胞元边长为5 mm的正六边形多胞鞋底结构的缓冲减振性能较优。
3)相同工况下及正六边形胞元的边长保持5 mm不变时,凹槽深度为2.5 mm的正六边形多胞结构鞋底的缓冲减振性能较优。
