基于近红外预测羊草水分含量的特征光谱模型研究
2019-12-20陈积山刘杰淋邸桂俐朱瑞芬孔晓蕾
陈积山, 张 强, 刘杰淋, 邸桂俐, 朱瑞芬, 孔晓蕾
(黑龙江省农业科学院草业研究所, 黑龙江 哈尔滨 150086)
羊草(Leymuschinensis)是我国重要的优良牧草之一,有着很高的经济价值和生态价值,被誉之“国草”。然而实际羊草的收获和储藏过程中极易受到生产地的水、土、气等的影响而发生营养成分损失或变质,目前我国羊草质量的低质化和劣质化现象普遍存在[1]。传统的感官评价和理化分析等检测方法耗时长,不能满足规模化羊草生产过程中的及时监测与测试要求,特别是羊草水分含量的快速定量预测存在困难。
随着新一代计算机的诞生和人们对偏最小二乘法(Partial least-squares regression,PLS)方法的深入研究,应用特定的化学计量方法筛选和选择,在预测待测样本或物质成分上具有特征波长或波长区间,有可能建立较好的光谱定量模型[2]。近红外光谱由于具有波长点数多、吸收度低、谱带归属难等特点,一般采用全谱分析方法从光谱中提取更多信息,然而事实上,近红外光谱中的某些波长所蕴含的信息,并不完全或几乎没有对模型的建立和校正都有贡献,恰恰相反,大量的无用波长携带的无用信息或噪声信号增加了模型的建立和分析运算时间,更有甚者常常会导致所建模型质量下降或不科学[3-4]。研究表明,特征波长优选可以具有简化模型,降低模型维数等特点,其优点在于剔除不相关或非线性变量因素的干扰,从而获得稳健性好、预测能力强的校正模型[5]。因此,近红外光谱建模过程中,在不损失必要信息的前提下,科学合理的缩小或选择光谱范围,可以减少无益信息对建模的负面影响,从而提高光谱建模的质量[2]。
目前,波长优选方法在近红外光谱研究中备受关注[5]。通常有4种常用的选择方法,这些光谱特征区间的选择方法主要包括间隔偏二乘法(Interval partial least-squares regression,iPLS)、向后区间偏最小二乘法(Backward interval PLS,BiPLS)、联合区间偏最小二乘法(Synergy interval PLS,SiPLS)、和连续投影算法(Successive projections algorithm,SPA)。本文在此基础上,深入探讨和分析 4种波长优选方法与PLS结合的模型预测能力,选择最适于预测羊草水分含量的敏感波长变量并建立高精度模型,以期为在田间管理、刈割储藏、家畜饲喂过程中对羊草水分参数的准确预测。
1 材料和方法
1.1 试验材料
试验于2014-2017年在黑龙江及内蒙东部草地选择单一羊草群落,6月初羊草基本处于抽穗期,其营养状况能代表其品质特点。每个样地以50亩不少于5个采样点为原则,收集地上5cm以上的羊草为待测样品,在实验室将其烘干过1mm筛后,装入自封袋常温避光保存,以备后期测定理化和光谱参数。羊草品质成分测试数据来自黑龙江农业部谷物及制品质量监督检测测试中心。
1.2 试验方法
首先将采集的羊草光谱进行预处理,再进行X-Y距离结合的样本划分法(Sample set partitioning based on joint x-y distance,SPXY)的样本校正集和验证集的划分[6]。通过PLS iToolbox工具箱,分别针对水分进行羊草光谱的特征波长筛选,筛选的方法[7]包括iPLS,BiPLS,SiPLS和SPA。将整个实验过程产生构建的预测模型,根据模型的评价参数分别进行择优比较,最后确定最佳预测模型,并通过泰勒图(Taylor)呈现。
泰勒图[8]是一种能可视化展示模型模拟值与观测值相似度的二维平面图形,泰勒图的主要目的是考察模型模拟值与实测值的相似度,同时评价其总体离散程度。特别适用于评价模型的模拟值与实际值的符合程度。主要选用相关系数(Correlation coefficient,R)、中心点之间均方根差(Centered root-mean-square difference,cRMS)和标准差(Standard deviation,SD)等指标量化评价模型模拟值与实测值之间的差异。
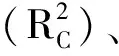
近红外光谱台式分析仪采用瑞典波通(Perten)公司二极管阵列近红外漫反射光谱仪(DA7200),样品池的光程为 13 mm,材质为石英试样杯。化学仪器:烘箱,瑞典福斯·特卡托2300全自动凯氏定氮仪(Foss公司),索式粗纤维测定仪Fibertec1020(Foss公司);IR35全自动快速水分测定仪,3次重复,均以干物质为基础。
1.3 数据处理
本试验采用MATLAB7.0 软件工具箱(iToolbox)建立羊草水分(Water)的关系模型。PLS iToolbox工具箱支持iPLS,BiPLS,SiPLS和SPA[10-12]。同时,借助SPSS17.0进行所有数据的整理和分析。
2 结果与分析
2.1 iPLS模型
iPLS法首先对全光谱均分成20个区间,在每个区间上进行PLS回归,以交叉验证的方法比较不同的PLS主成分数对应的校正均方根误差RMSECV值,选择最小RMSECV值对应区间进行建模。结果表明,羊草样品水分含量的主成分数在5时对应的RMSECV最小,此时iPLS建立羊草样品水分含量的模型结果如图1。图中曲线代表任意一份羊草样品的近红外光谱,柱形图内的斜体数字代表相应区间的最佳主成分数,虚线代表选择5个主成分数时全光谱建立PLS模型预测羊草水分含量的RMSECV值。如图1所示,3个区间的RMSECV值都比全光谱建立PLS模型的RMSECV小,其中iPLS选取1个最佳波长区间的RMSECV值最小,这表明该区间的近红外光谱所包含的相对有益信息较多,该光谱区间在全光谱范围的位置如图1,对应波长范围1 250~1 305 nm。因此,利用区间波长1 250~1 305 nm的所有羊草样品进行分析建模(图2),该区间建立的最佳PLS模型的结果见图3(a,b)。
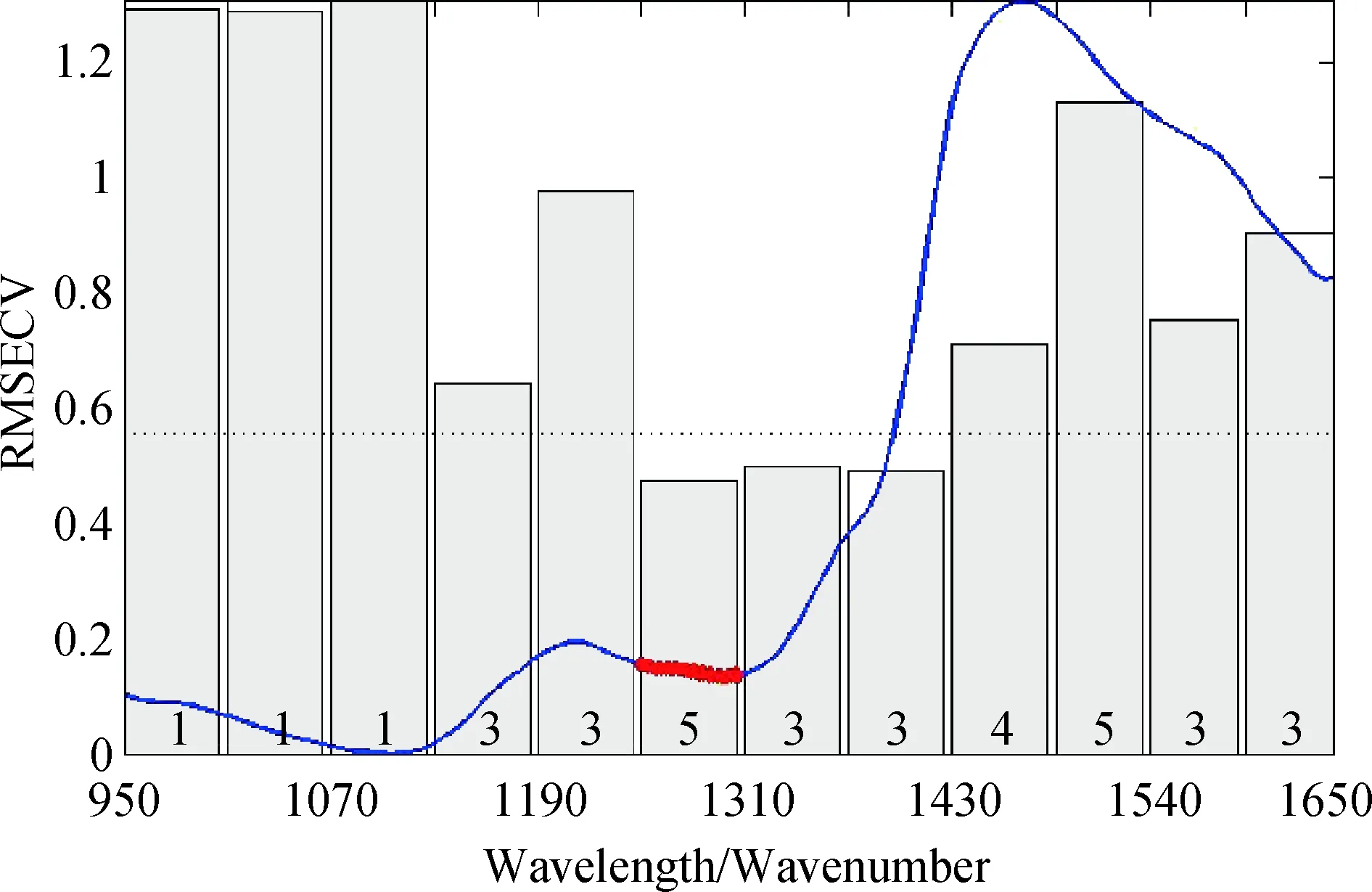
图1 不同区间iPLS模型对应的RMSECVFig.1 RMSECV corresponding to different interval iPLS modeling

图2 iPLS方法下光谱特征选择结果Fig.2 Selection of spectrum characteristic intervals by iPLS
通过对比发现,采用最佳1个区间(图3a)与全光谱(图3b)建立PLS模型结果不同。通过采用间隔偏二乘(iPLS)方法选取不同波长区间,建立的模型与全光谱建立的模型结果表明,相关系数R由0.9154提高到0.9411,RMSECV由0.5551降低到0.4725,但偏差效果明显比全光谱建模好,同时经过iPLS特征光谱区间选择后模型的预测精度高,由于iPLS采用变量数(波长点数55个)比全光谱少(波长点数141个),不仅降低了模型运算时间,而且也优于全光谱时的预测精度。

图3 模型性能比较Fig.3 Comparison of model performance
2.2 BiPLS模型
BiPLS(Backward interval PLS,向后区间偏最小二乘法)将全光谱950~1 650 nm分为10个区间,通过BiPLS方法对校正集的光谱数据进行区间选择,并进行交叉验证分析建模,整个运算过程与结果如表1所示。通过表1可知,随着剔除区间的减少,模型的RMSECV值在开始时表现减小,随着剔除区间数目的增加,RMSECV表现逐渐增大,这些变化表明,前者剔除的区间为噪声区间,后者剔除的区间包含有用信息,因此在RMSECV最小时,即为最佳的波长区间。结果表明,当剔除区间数目为4个时,其RMSECV达到最小为0.4170,此时对应6主成分因子,选择了85个波长变量数,剩余的区间为6个。
通过交叉验证分析剩余的6个区间的序号分别是第1,2,7,10,9,6区间(图4),对应的波长分别为950~1 020 nm,1 025~1 090 nm,1 305~1 370 nm,1 375~1 440 nm,1 515~1 580 nm和1 585~1 650 nm,建立的PLS最佳模型如图5所示,此时模型校正集的相关系数R为0.9537,交互验证均方根误差RMSECV为0.4170,偏差值为0.0052,同时BiPLS建立的羊草样品水分含量近红外PLS预测模型,其波长变量数从141个减少到85个,明显提高了模型运算速度。
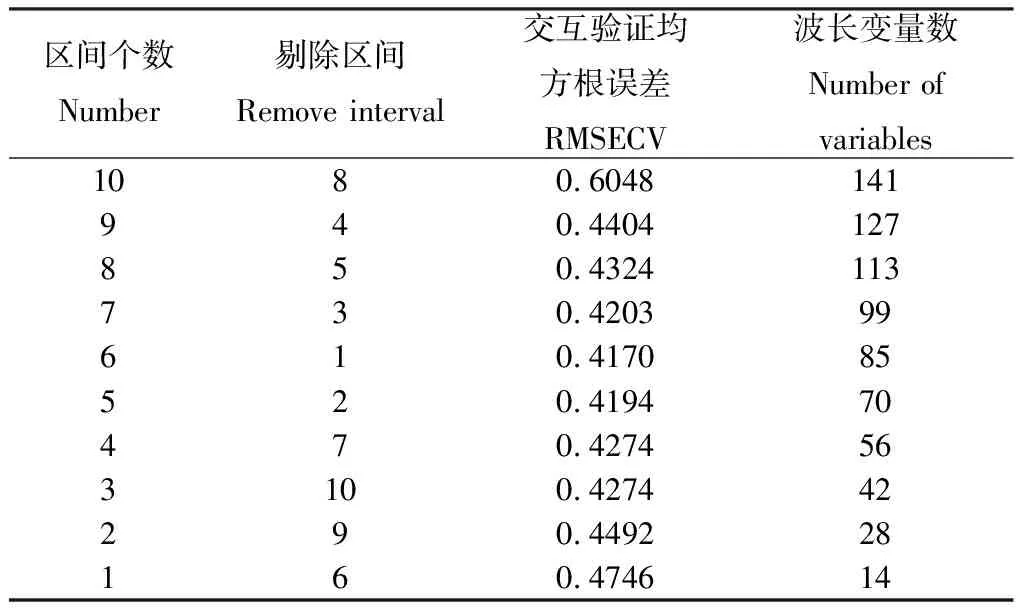
表1 不同区间选择的BiPLS建模结果Table 1 BiPLS modeling results of different interval

图4 BiPLS方法下光谱特征选择结果Fig.4 Selection of spectrum characteristic intervals by BiPLS
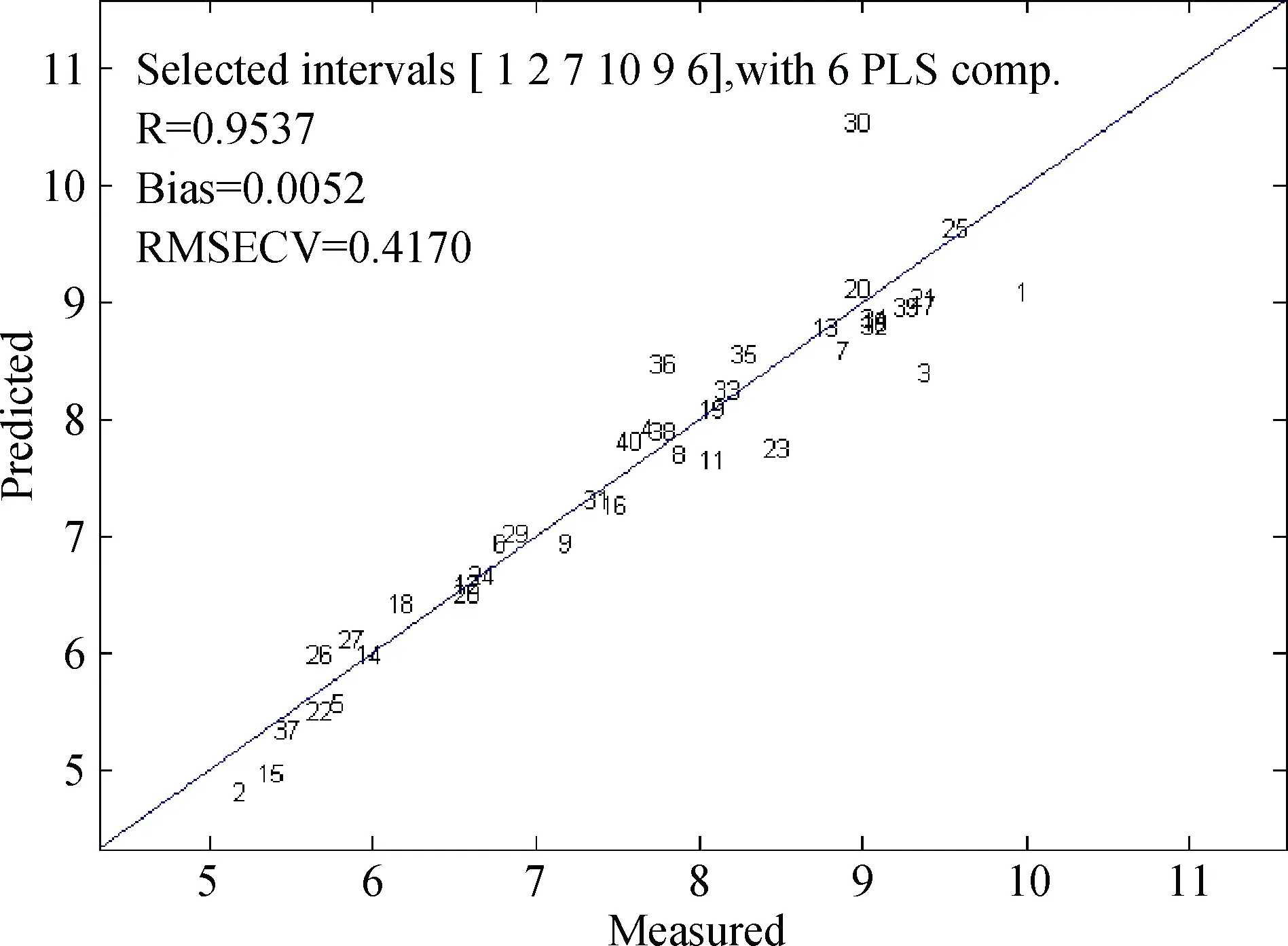
图5 BiPLS方法建模结果Fig.5 BiPLS modeling results
2.3 SiPLS模型
SiPLS(Synergy interval PLS,联合区间偏最小二乘法)对全光谱(950~1 650 nm)进行区间分割,将全光谱区间分成子区间10个,对产生的10个区间分别通过联合区间偏最小二乘法(SiPLS)进行PLS建模研究,通过预算最终确定最佳的区间组合。本研究中对羊草样品水分含量的光谱波长分别采用联合任意2个、3个和4个区间进行PLS建模,发现通过联合4个光谱区间时,其建模结果的交互验证均方根误差RMSECV最小为0.3823,其主成分数为5,选择区间为4,5,6,10(表2)。

表2 联合4个区间的BiPLS建模结果Table 2 BiPLS modeling results of 4 interval combination
以RMSECV值最小为依据,确定SiPLS选取4个最佳联合区间,其对应区间位置在全光谱上分别为第4,5,6,10个区间,其波长范围分别为1 165~1 230 nm,1 235~1 300 nm,1 305~1 370 nm和1 600~1 650 nm(图6)。采用4个区间联合建立PLS模型结果见图7所示,在第4,5,6,10个区间组合时,RMSECV值达到最小,此时对应模型最佳最优。以这4个区间在主成分子数为5时,建立PLS模型的相关系数R,RMSEC,Bias分别为0.9613,0.3823,0.0148。

图6 SiPLS方法的光谱特征选择结果Fig.6 Selection of spectrum characteristic intervals by SiPLS

图7 SiPLS方法的建模结果Fig.7 SiPLS modeling results
2.4 SPA模型
SPA(Successive projections algorithm,连续投影算法)对羊草样品水分含量进行SPA波段筛选(图8),由图8可知,经SPA筛选,确定最佳的光谱变量总数时交叉验证均方根误差RMSECV值最小为0.3321,羊草样品水分含量从141个波长点中筛选得9个特征波长点分别是35,55,76,89,93,98,121,135,141,其波长点位置分布在1 120 nm,1 220 nm,1 325 nm,1 390 nm,1 410 nm,1 435 nm,1 550 nm,1 620 nm,1 650 nm。从所选光谱变量的波长点可知,特征波长大部分都分布在近红外光谱波段(1 120~1 650 nm),说明对羊草样品进行水分含量检测时近红外光谱起到了比较大的作用。在SPA筛选结果基础上,建立羊草样品水分含量指标的SPA-PLS模型,模型计算结果如图9所示,经SPA波段优选,羊草样品水分含量指标的模型预测相关系数R为0.9525,预测标准偏差RMSEP达到0.3324。
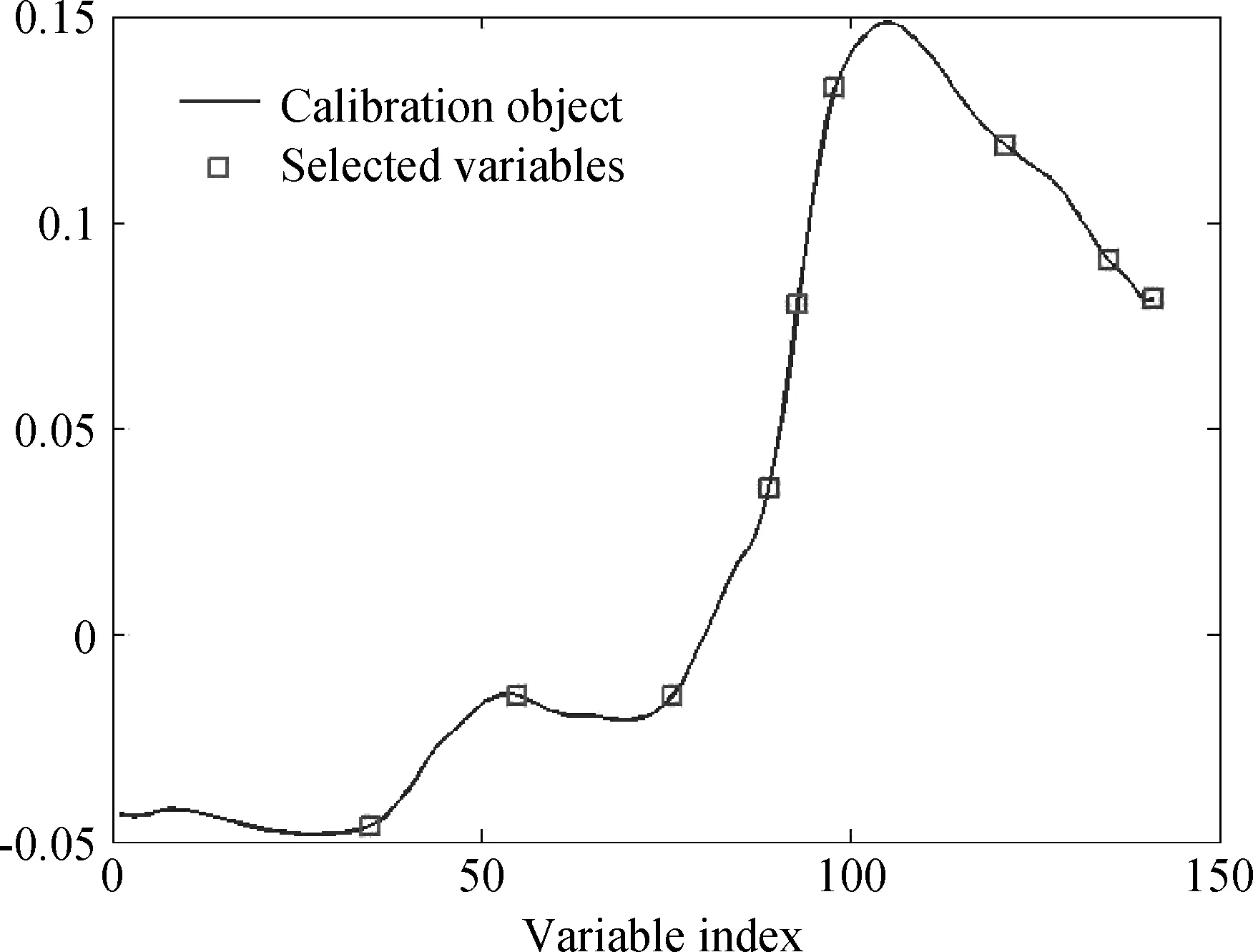
图8 SPA筛选的相应波长点Fig.8 The corresponding wavelength points by SPA selection
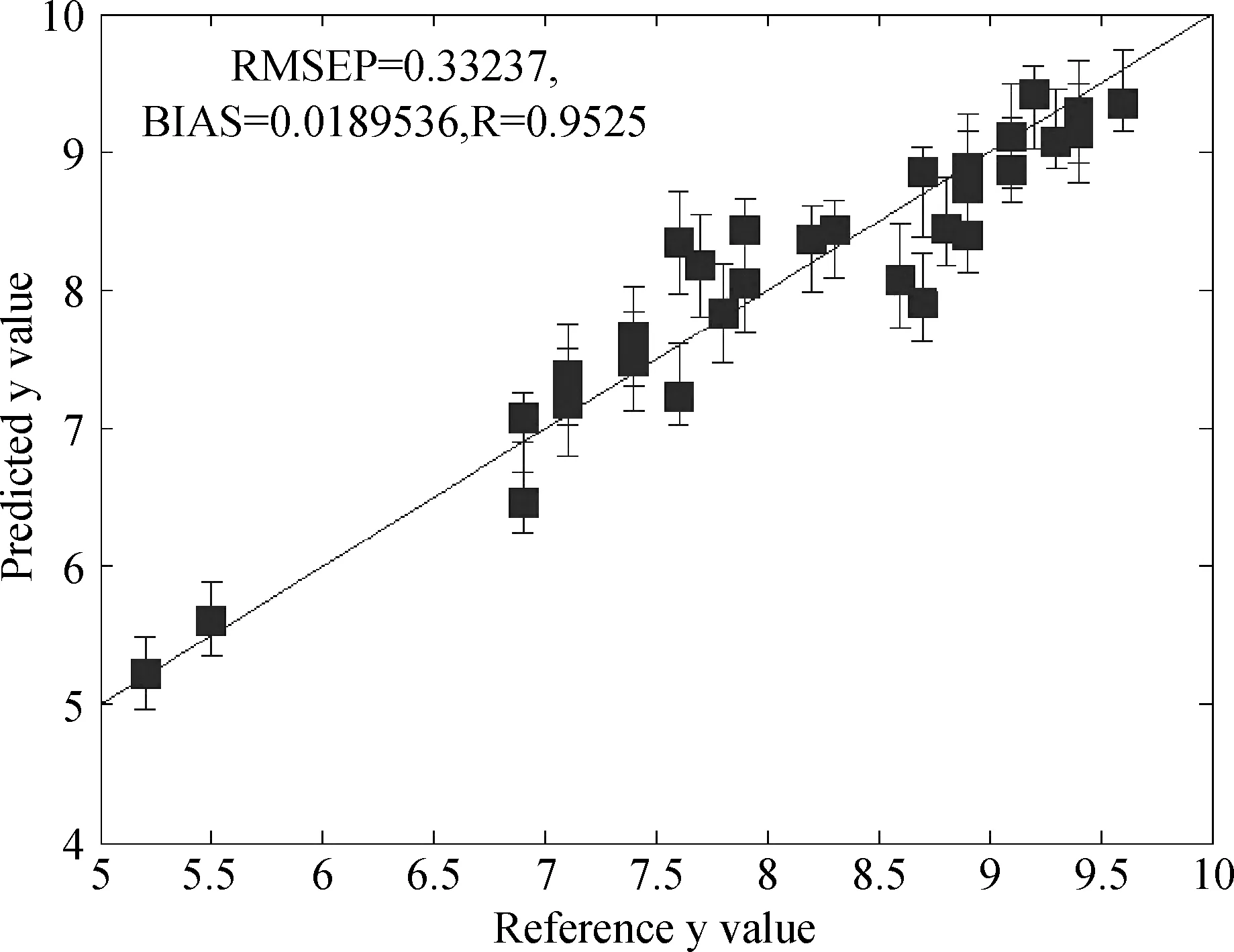
图9 SPA模型的验证结果Fig.9 SPA modeling results
2.5 不同特征波长选择方法下模型性能比较
通过iPLS,BiPLS,SiPLS,SPA-PLS四种特征波长选择方法[13-17],分别建立羊草水分含量模型的预测性能如表3所示,与全光谱建立模型的预测精度相比,特征光谱区间选择或波长选择后模型的预测精度均存在明显不同。从波长变量数来看,四种特征波长选择方法采用变量数均少于全光谱PLS模型选择的波长变数,其中SPA-PLS选择的波长变数最少为9个,占全光谱变量数的6.3%;其次是SiPLS选择的波长变数为49个,占全光谱变量数的34.8%;iPLS和BiPLS选择的波长变数分别为55和85个。从模型的三个评价参数(R,RMSEP,RPD)来看,iPLS建立的羊草水分含量预测模型最差,其预测结果与实测结果的相关系数R达到0.9411,预测均方根误差RMSEP为0.4725,相对分析误差RPD为2.419。SiPLS建立的羊草水分含量预测模型参数最优,其预测结果与实测结果的相关系数R达到0.9613,预测均方根误差RMSEP为0.3823,相对分析误差RPD为2.648。
同理,通过泰勒图10也表明,SiPLS方法最适合特征波长的筛选来预测羊草水分含量。图中绿色弧度实线为羊草水分预测值中心点与观测值中心点之间的均方根误差cRMS;黑色弧度实线为经标准化的实测标准差SD;黑色0.5虚线表示模型预测SD是实测值SD的一半,黑色虚直线表示模型预测SD是实测值SD的1.5倍。SiPLS方法模拟值与实测值(绿色方块)的相似度最高,相对分析误差RPD最小(表3)。
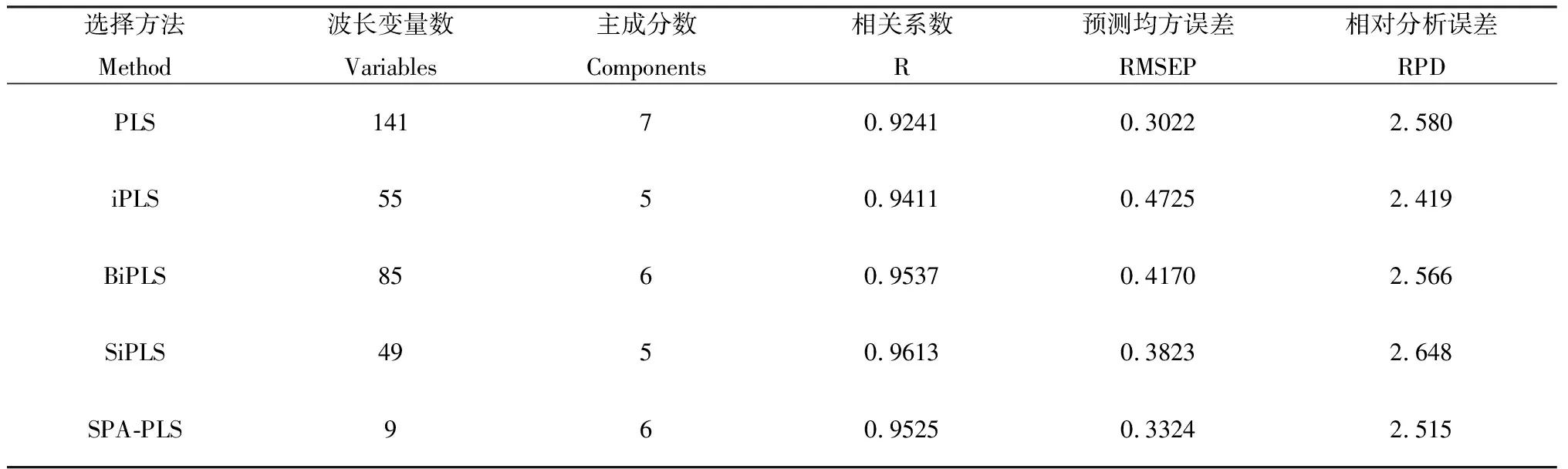
表3 不同选择方法及所建模型性能比较Table 3 Characteristic wavalength selection method and comparison of model perfomance

图10 不同模型的泰勒图Fig.10 Different models in chart of Taylor
3 结论
与全光谱PLS方法相比,BiPLS,SiPLS,SPA-PLS均能适合羊草水分含量特征波长的确定。从最终选择的特征光谱区间和特征波长来看,SiPLS选择的特征区间证明已包含在最优的区间中,其中SiPLS方法最适合用于羊草水分含量特征波长的筛选,其次为BiPLS方法,最差的方法为iPLS。该研究结果可为预测羊草及其相关禾本科牧草水分含量切实有效,预测精度在96.13 %以上。
