基于电网结构的电压稳定性分析实验教学设计

王 蕾, 姜志海，张新慧

(山东理工大学 电气与电子工程学院，山东 淄博 255049)

0 引 言

电力系统的静态电压稳定性是在正常运行或受扰情况下，电力系统能够维持母线电压在可接受的稳态值的能力[1]。该部分内容是研究生课程“现代电力系统分析”的必修内容，也是电气工程专业教学中的重点讲授内容。相比对本科生的教学，硕士生阶段的学习内容更加深入，因此需要导师或授课教师在传授过程中给以引导和启发。

采用电力系统软件包的教学方式已经广泛应用于各大高校的电气工程专业本科生和研究生的“电力系统分析”课程教学中[2-4]。这种教学方式或实验方式，通过课堂演示可以增强学生对“电力系统分析”课程中众多抽象概念的理解；通过实验教学，学生可以反复运行软件程序，测试不同条件下系统各状态量的变化，有助于教与学的互增互助，同时还避免了实物物理实验平台的高额投入与危险操作等问题[5]。

为加深学生对电压稳定性分析内容的理解和掌握，促进科研成果与教学资源的互助，本文设计了以Matpower为仿真工具的电力系统静态电压稳定性分析与计算的虚拟实验教学环节，教学过程中注重理论知识与实验结果的统一，采取多种教学手段与方法(如增设问题导向引导学生的独立与深入思考)，由浅入深地导入科研方法与创新意识，培养学生主动思考、主动探索的科研能力，激发学生求学—求知—钻研的工匠精神[6-8]。

1 电压稳定分析方法

连续潮流法(又称延拓潮流)是目前广泛应用的分析电力系统静态电压稳定性的实用方法。该方法可得到系统在某个功率增长方向下的P-U曲线和Q-U曲线，利用曲线拐点(又称鼻点)信息得到电力系统的电压稳定性和稳定裕度。结合特征分析方法可以计算连续潮流代数方程组在各个运行点的雅可比矩阵特征值来分析系统的稳定性。若存在实部为正的特征值时，则系统在该点处是电压不稳定的。

电力系统电压不稳定的物理解释是负荷需求大于系统网络的最大传输能力[1]。对一端为恒定电压源的简单二端口网络，可以通过推导数学模型算出该网络的最大传输功率。然而对复杂电力网络或大规模电力系统的电压稳定性分析，必须借助计算软件和合适的数值方法。Matpower是基于Matlab平台开发的电力系统分析开源软件，最新版本的Matpower 7.0b嵌入了连续潮流方法，为复杂电力系统的电压稳定性分析提供了有力的计算工具。

优化电力系统的网络结构是对电网现有资产的优化利用。相比于常用改善系统电压稳定性的其他措施(如无功补偿、变压器分接头控制、发电计划重新调度、切负荷等措施)，优化电力系统的网络结构也可以有效改善系统电压稳定性，并且该方法有效利用了电网的固有资产，大大减少无功设备的投入和维护成本，更经济，操作更方便。因此该措施是当前应用于电力系统各研究领域的研究热点。

2 实验算例及参数

仿真算例以IEEE 9节点标准算例为基础修改而成，电网拓扑结构、线路及变压器支路参数、负荷及发电机注入功率增长方向如图1所示。潮流计算必要的数据参数见表1。

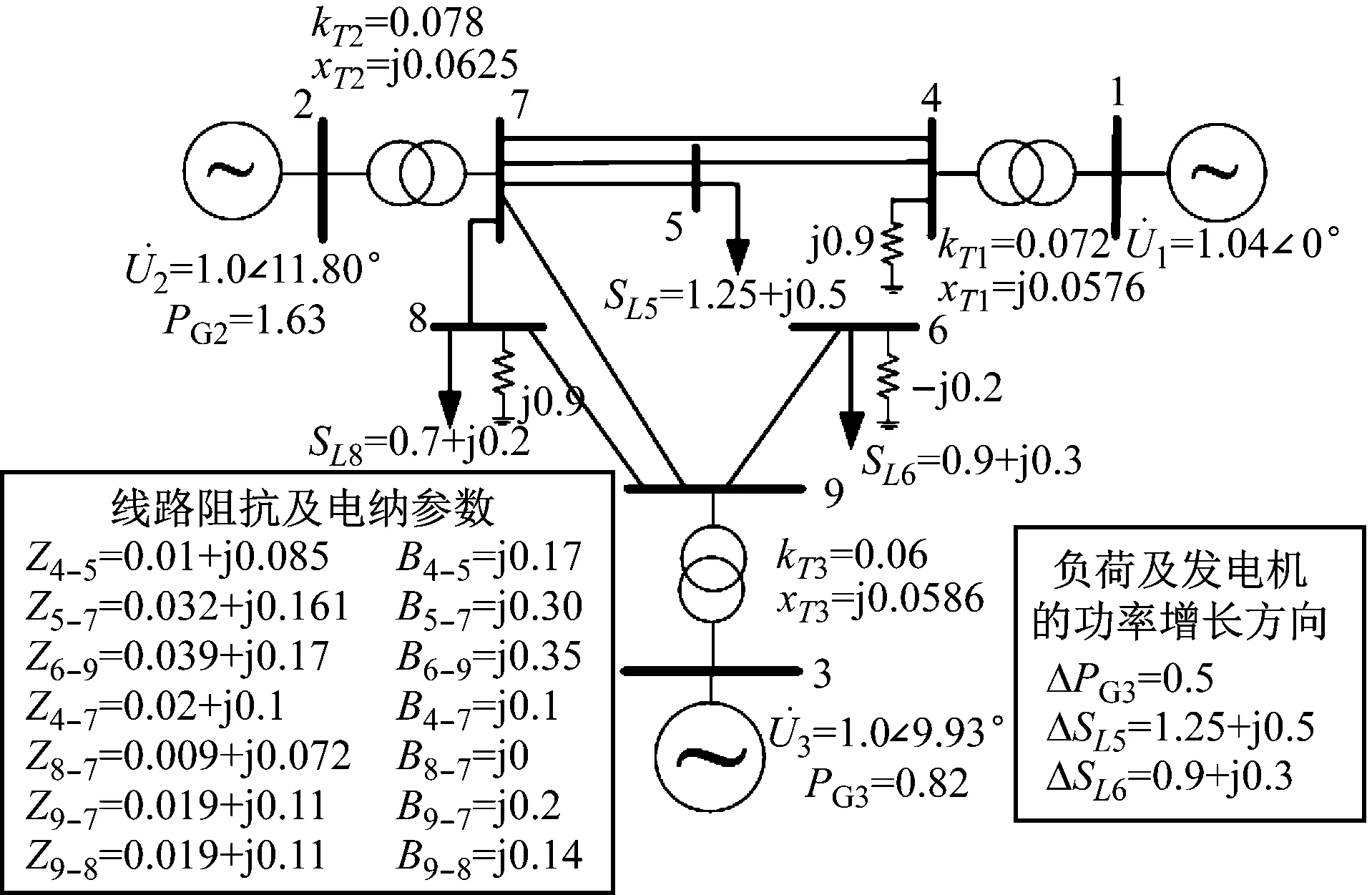
图1 实验算例系统及参数

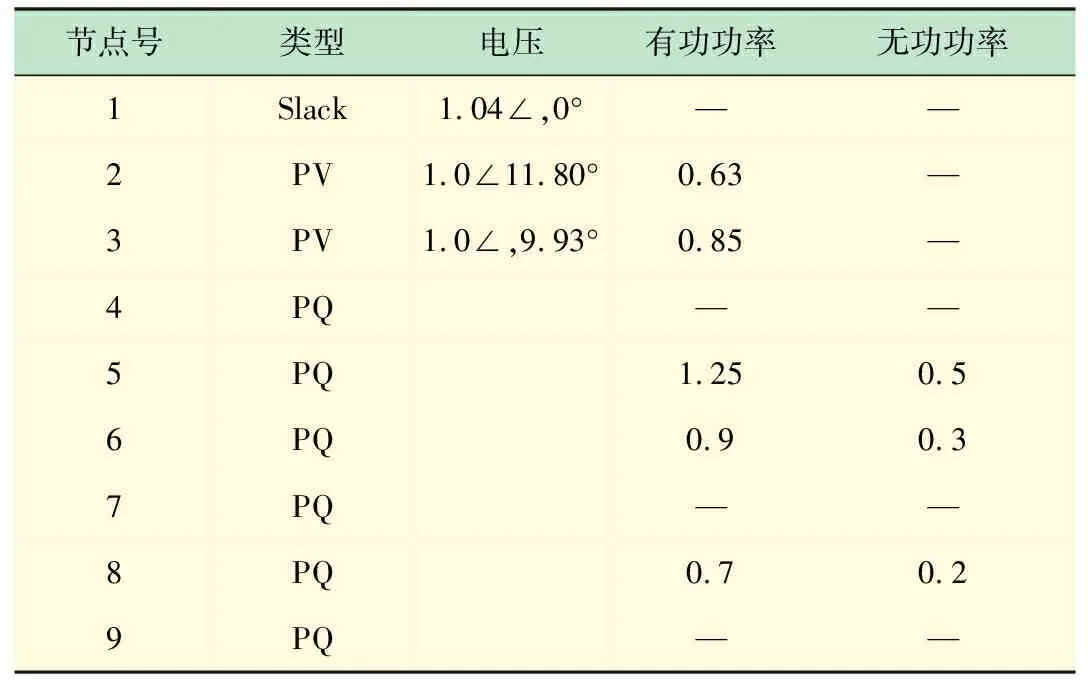
表1 实验算例基本参数(标幺值)

3 电网拓扑结构对鞍结点分岔的影响

不考虑发电机无功极限时，负荷及发电机功率沿预定的方向增长，电力系统有可能发生鞍结点分岔(Saddle-Node Bifurcation，SNB)的局部分岔现象。从物理本质上讲，SNB是由于电力网络的传输能力达到极限而表现出的一种非线性光滑电压失稳。通过输电线路切换或改变母线运行方式的措施也可以控制电力系统SNB的发生[9-11]。

3.1 输电线路开断

实验中测试3种网络结构的电压稳定性，分别为基态电力系统(见图1)、开断线路8-9后电力系统和开断线路7-9后电力系统。

根据图1中的数据，分别生成Matpower连续潮流计算所需的两个数据文件：‘base case data’和‘target case data’，对如上3个电力系统分别运行连续潮流程序。实验仿真结果为：基态系统负荷裕度λ=0.671 9；开断线路8-9后电力系统的负荷裕度λ=0.714 83；开断线路7-9后电力系统的负荷裕度λ=0.588 8。输电线路开断前后母线6的P-U曲线如图2所示。

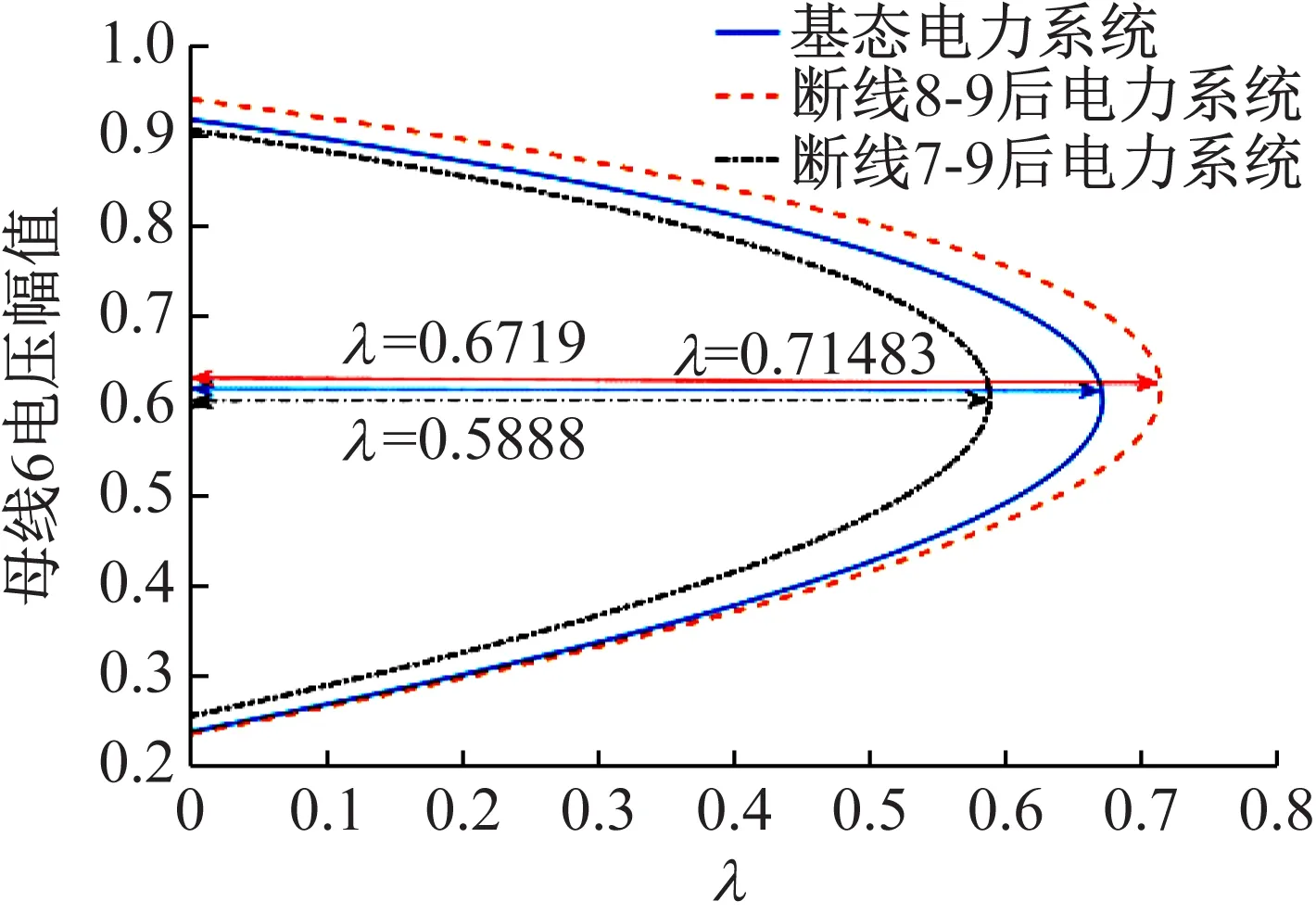
图2 3种电网拓扑结构下的P-U曲线和负荷裕度

3.2 母线解列运行

实验中测试2个网络结构的电压稳定性，分别为基态电力系统(见图1)和解列5号母线后的电力系统(见图3)。

图3 5号母线解列运行的拓扑结构示意图

根据母线解列前后场景，分别修改Matpower连续潮流计算所需的数据文件：‘base case data’和‘target case data’，然后对如上3个电力系统分别运行连续潮流程序。注意解列母线后的电力系统base case data文件需要增加1个节点。实验仿真结果为：解列后系统在该功率增长方向下的负荷裕度λ=0.687 8。母线6的P-U曲线如图4所示。

图4 母线解列前后P-U曲线和负荷裕度

3.3 实验结果分析

分析上述仿真实验结果，相对于基态系统的负荷裕度，开断线路8-9后系统的负荷裕度增加了6.39%；开断线路7-9后电力系统的负荷裕度减小12.37%；解列母线后系统的负荷裕度增加了2.37%。输电线路开断和母线解列运行使得电力网络产生不同拓扑结构，在相同的功率增长方向下，其表现出了不同的电压稳定能力。因此通过输电线路的开断和母线解列可以增大或减小电力系统由鞍结点分岔约束的电网传输能力。

4 电网拓扑结构对结构诱导分岔的影响

通常在潮流计算和连续潮流计算中，发电机节点被认为是PV节点，即该发电机具有无限的无功功率调节能力，能够维持该节点电压恒定。然而负荷增长过程中系统的电压水平降低导致发电机无功出力逐渐增加，实际发电机的无功出力并不是无限大的，因此当达到无功限值时，发电机不再具有电压调节能力，不能维持恒定的机端电压，此时该节点类型由PV节点转为PQ节点。当系统中的某台发电机无功出力达到极限时，电力系统的稳定平衡点会就突然消失，从而造成电压崩溃。此时电力系统发生结构诱导分岔(Structure-induced Bifurcation, SIB)，又称极限诱导分岔(Limit-induced Bifurcation，LIB)，这是一种由于发电机无功出力达到极限而表现出的非线性非光滑性的电压失稳。

本节给出两个实验算例，学生可以通过仿真实验的方式，体会SNB和SIB的区别，研究输电线路开断和母线解列的运行方式对结构诱导分岔的影响。

4.1 输电线路开断

本节采用基态电力系统和开断线路8-9后电力系统作为研究对象。设置发电机2、3无功功率输出范围为[-100，90]Mvar。经仿真可得，计及发电机无功限值的基态电力系统负荷裕度λ=0.474 65；开断线路8-9后的电力系统负荷裕度λ=0.553 62。P-U曲线及雅可比矩阵特征值如图5～7所示。

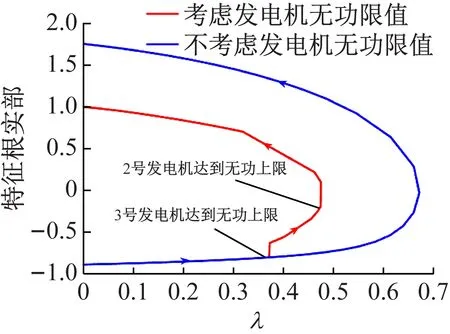
图5 雅可比矩阵主导特征值变化图

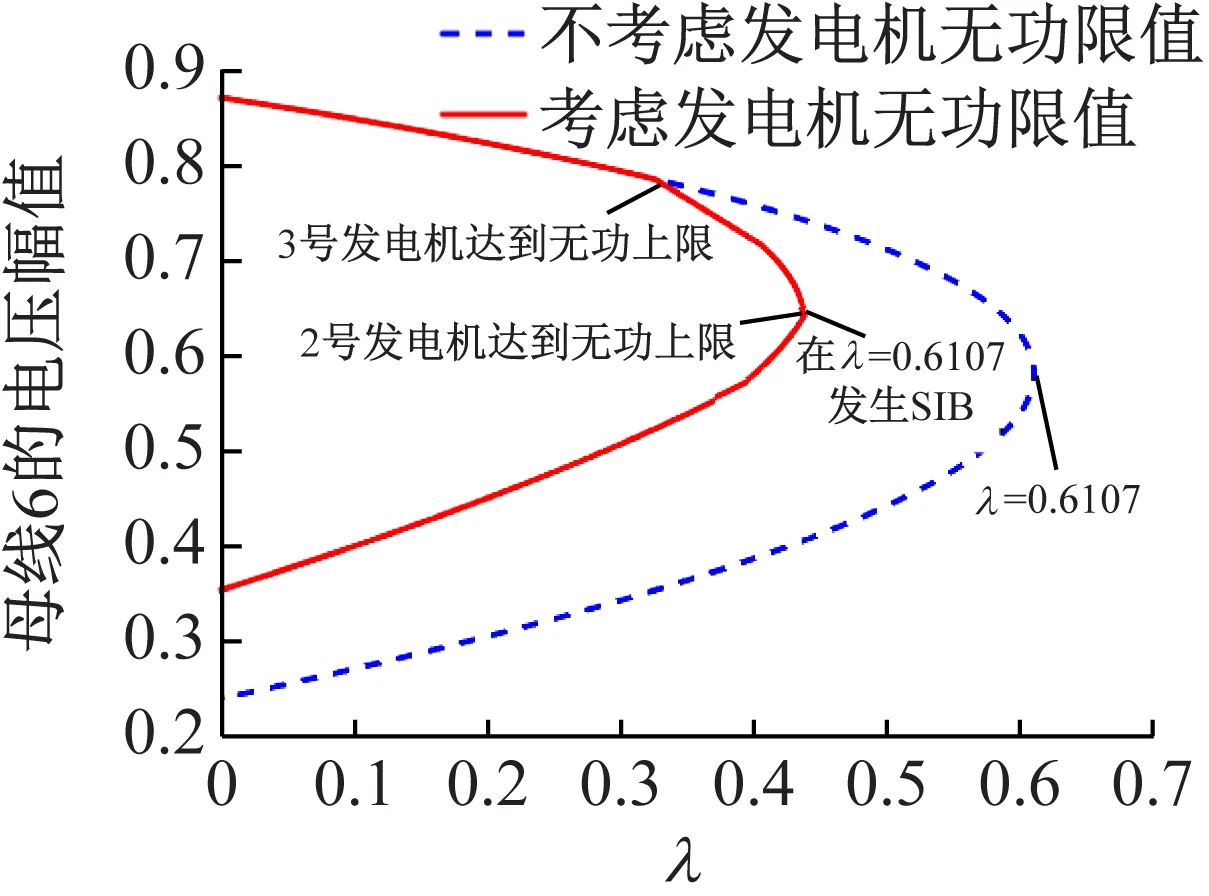
图6 基态电力系统的P-U曲线

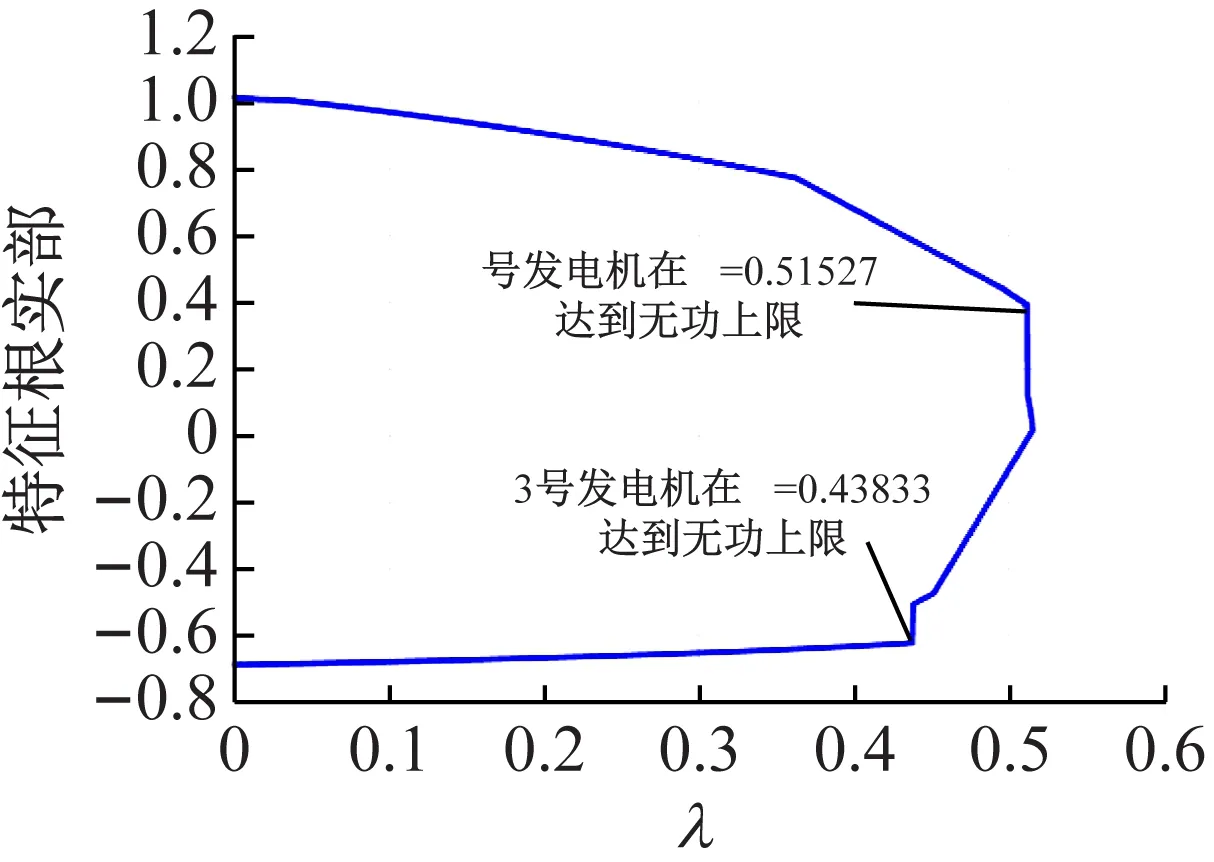
图7 雅可比矩阵主导特征值的变化

分析实验结果可得：考虑发电机无功出力限值时，随着功率需求增长，发电机3在λ=0.372 25达到无功出力上限，其节点类型由PV节点转为PQ节点，此时计算潮流方程雅可比矩阵特征根可发现，全部特征值仍然位于左半开平面(图5给出了主导特征值的变化情况)，系统的稳定性不变。随着功率需求的继续增长，发电机2在λ=0.474 65时无功出力达到上限，其节点类型发生转变，转变前后雅可比矩阵的主导特征值实部符号由负转正(见图5)，因此可以判断该情况下电力系统发生了结构诱导分岔。比较计及发电机无功出力限值前后，基态系统的负荷裕度为从0.671 9(见图2)降低至0.474 65(见图6)。因此由于发电机无功出力的限制，基态电力系统的负荷裕度降低了29.36%。

4.2 母线解列运行

本节采用3.2节的两个电力系统作为研究对象。设置发电机2、3无功功率输出范围为[-100，90]Mvar。经仿真可得：计及发电机无功限值的解列后电力系统的负荷裕度为0.515 53。

分析实验结果可得：考虑发电机无功出力限值时，随着功率需求增长，发电机3在λ=0.438 33达到无功出力上限，其节点类型转变(PV转PQ)，此时分析主导特征值(见图7)可得此时系统的稳定性不变。随着功率需求的继续增加，λ=0.515 53时系统的稳定性发生改变。分析雅可比矩阵的主导特征值实部的变化(见图7)可知，主导特征值的实部有负转正并不是由于某台发电机无功达到限值所致，因此系统发生了鞍结点分岔(SNB)。

不考虑发电机无功出力范围时，解列后电力系统的负荷裕度为0.68 78；而考虑发电机无功出力限值时，解列后电力系统的负荷裕度为0.515 53。由于限制了发电机无功出力，电力系统的负荷裕度降低了25.05%。

4.3 实验结果分析

分析上述仿真实验结果，开断输电线路8-9后电力系统和母线解列运行电力系统(见图3)均可以不同程度的增大基态电力系统由结构诱导分岔约束的负荷裕度(见图8和9)。根据4.1和4.2的实验示例，可以得出：输电线路开断和解列母线且选择合适的母线解列场景对结构诱导分岔也有明显的延迟效果。

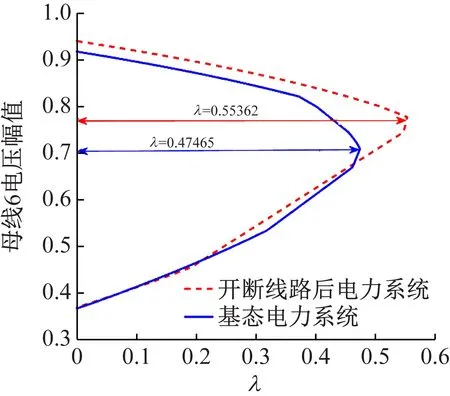
图8 基态电力系统和开断线路8-9后电力系统的P-U曲线

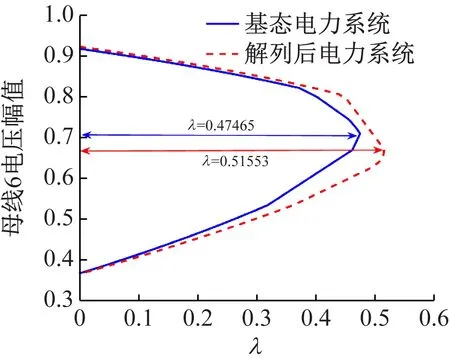
图9 基态电力系统和母线解列后电力系统的P-U曲线

为进一步加深学生对考虑发电机无功出力时电压失稳情况的理解，表2中列出了几种拓扑结构下发电机发出的无功功率随负荷裕度的变化情况。分析可得如下结论：

(1)基态电力系统：随着负荷的增长，发电机G3和G2相继达到出力极限，且由G2的无功越限导致结构诱导分岔。

(2)由于线路8-9的开断，减小了G3在初始潮流时承担的无功功率，因此延缓了G3无功越限的发生。

(3)随着功率需求的增加，发电机G2首先无功越限，其次是发电机G3，最后系统发生结构诱导分岔；

(4)由于线路5-7的开断，加重了发电机G3、G2在初始潮流时的无功出力。当功率需求增加时，两台发电机很快达到无功出力上限，依次发生无功越限，最终导致系统发生结构诱导分岔。

5 虚拟实验教学环节设计

采用理论与仿真实验相结合的教学模式[12-14]，可以充分利用各自的优势，实现取长补短，优势互补，提高学生对理论知识的理解能力，同时教师在教学过程中采取合适的教学手段，引导学生体会从发现问题—思考问题—解决问题的科学研究过程，提高学生的动手实践能力和创新思维的培养。结合本虚拟实验的相关理论知识点和该实验的具体特点，本实验教学环节适合采用任务驱动法、问题导向法和讨论法相结合的教学方法。实验前可以将学生分组，便于学生相互讨论，共同学习。实验教学中教师应注重设置问题，用问题启发学生，并逐层递进地加大问题难度，引导学生思考和解决问题，培养学生的科学研究兴趣。

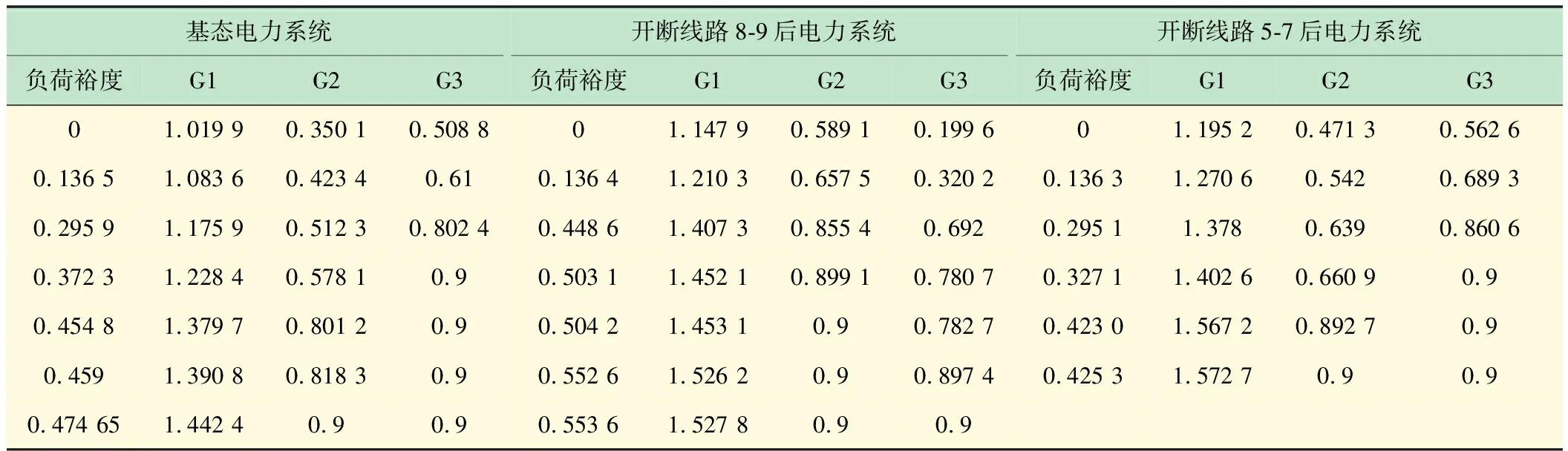
表2 各拓扑结构下的各发电机无功输出(标幺值)

根据该实验的具体内容，针对不同的仿真实验内容和进度，设置了如下分阶段的引导式问题[15]，以便激励学生进一步探究和思考：

(1)研究输电线路投入、实验仿真系统中其他输电线路切换和母线解列场景对鞍结点分岔和结构诱导分岔引发的电压失稳的影响。该问题是前述实验内容的延伸，教师可以鼓励学生独立完成仿真实验，并给出实验结论。

(2)研究开断相同线路或母线分裂运行场景下，负荷和发电机功率增长方向不同时的电力系统电压稳定性。教师可以引导学生仿真在不同功率增长方向下的电压稳定裕度，计算和分析功率增长方向与电压稳定裕度的关系。

(3)研究其他控制措施对电压稳定性的影响，如无功补偿装置、变压器分接头变化、切负荷等。在前述实验系统中改变无功补偿装置的安装位置和容量、变压器分接头的位置，用仿真实验的方式得到增强电压稳定性的灵敏节点，对比这些控制措施的效果。

6 结 语

本文以电力系统分析课程为基础，结合作者的科研成果，设计了以Matpower为仿真软件的电压稳定性分析虚拟实验教学课，重点研究电网拓扑结构对电压稳定性的影响和作用，通过对输电线路开断、母线解列运行的方式改变拓扑结构，从而改变电力系统的电压稳定性。

该实验的设计是电压稳定性理论教学的延伸和拓展，实验设计注重以学生为主体的教学方式，通过问题导向引导学生从仿真中获得理论知识、从实验中探索、从结果分析中返回理论知识的过程，可以有效增强学生对知识的理解，并从中体会从事科学研究的过程。