同轴特性阻抗电磁场综合实验
2019-12-20骆新江张忠海
骆新江,张忠海
(杭州电子科技大学 电子信息学院,杭州 310018)
0 引 言
电磁场与电磁波课程是电子信息类学科发展的基础,如通信、电子、电气工程、机电、生物等[1-5]。然而,电磁场与电磁波课程是目前公认的教师难教、学生难学的一门课程[6-7]。大量物理实验固然可以帮助学生理解相关概念和理论,但是弊端也是显而易见的,一方面设备费用极为昂贵,还需要额外配置场地;另一方面还受时间和地点的限制[7]。商用电磁场与电磁波仿真软件的发展已经可以非常精确地模拟相关工程实际[8-12]。采用虚拟仿真实验不仅能够达到物理实验的效果,而且还可以将场分布可视化呈现出来,这一点是物理实验所无法比拟的。基于虚拟仿真实验的这些优点,所以近些年来出现了不少的成功案例[13-17],但大多数案例都是针对某个单一理论而设计的,所以学习效率较低,且对学生综合应用能力的培养作用不大。本文构建了同轴传输线特性阻抗综合实验,将均匀平面波理论、传输线理论、静电场理论和静磁场理论柔合在一起。同时,考虑到同轴传输线是射频微波系统中最为常用的传输线之一,它不仅用于各种微波设备间的连接线,而且还常制作成各种微波器件,如同轴滤波器、同轴分配器、同轴天线、同轴开关等。
1 理论分析
1.1 基于场论的同轴传输特性阻抗
如图1所示,同轴线由内、外导体和内部介质填充物构成。设导体均为理想导体,内导体的半径为a,外导体的内半径为b;介质为理想电介质,介电常数为ε(等于相对介电常数εr和真空介电常数ε0的乘积),磁导率为μ(等于相对介电常数μr和真空介电常数μ0的乘积)。

(a)三维示意图

(b)横截面示意图
基于以上假设的同轴线为无耗理想传输线,所以同轴线中传播的是横电磁波,因此同轴线中的电场和磁场满足以下波动方程[18]
(1)
式中,下标t代表横向。柱坐标下上式可写为
(2)
引入标量电位函数Φ(r,φ),则在同轴线纵向z位置处的横截面上,电场和电位的关系为
(3)
代入式(2),结合场的对称性可推得同轴线内电位所满足的拉普拉斯方程
(4)
通解为
Φ=A·lnr+B
(5)
式中:A,B为待定常数,代入边界条件,并利用式(3)可解得电场分布。由获得的电场分布,再利用麦克斯韦方程中的法拉第电磁感应定律可求得磁场分布。将两解写在一起,即
(6)
根据求得的电场和磁场可以求出电压U和电流I的分布:
(7)
从而可知特性阻抗为:
(8)
对大多数材料而言,相对磁导率μr≈1[18],因此对于此类电介质构成的同轴线特性阻抗可以写为
(9)
以上从“场”的角度,利用均匀平面波传输理论,阐述了同轴特性阻抗的物理实质。下面用“路”的理论再来解释。
1.2 基于“路”理论的同轴特性阻抗的
实践证明,当电路尺寸远小于传输波长时,电路分析理论是正确的。基于此,为了利用电路理论分析传输线,可将一根传输线看成是由若干段无限短的传输线组成,使每段传输线的物理长度都远小于传播的电波长,这时就可以将每段传输线用等效的集总参数电路来表示了,于是就可以用电路理论对每段传输线进行分析了。
取出一小段长度为Δz的传输线,其等效电路如图2所示[18]。图中:L为分布电感,即单位距离电感;C为分布电容,即单位距离电容。则长度为Δz的传输线具有总的电感量为L·Δz,总的电容量为C·Δz。两端电压电流分布如图2所示。利用基尔霍夫电压定律和电流定律分析此等效电路,传输线方程

图2 无耗传输线Δz线段等效电路图
(10)
将耦合的电压和电流分离后可得电压和电流的波动方程
(11)

上述波动方程的通解同样为入射波+反射波的形式,即
(12)
根据传输线特性阻抗的定义式:
Z0=U+/I+=-U-/I-
可推得无耗传输线的特性阻抗为:
(13)
可知,如果能够知道传输线的分布电容和分布电感,就可以求得特性阻抗。
由电磁场与电磁波理论可知,分布电容和分布电感可以利用静态场知识求得。
1.3 基于静电场理论的同轴分布电容
设同轴线导体上的线电荷密度为ρl,取如图1中所示的高度为1个单位,半径为ρ的高斯面,即虚线位置。对此高斯面利用静电场高斯定律,可求得同轴线中的电场分布为
(14)
从而由电压与电场关系可求得两导体之间的电压为
(15)
再利用电容定义式,即可求得分布电容。
(16)
1.4 基于静磁场理论的同轴分布电感
由于各导体的内自感与外自感相比很小,故忽略不计,这里只考虑外自感。假设,通过如图1所示的同轴线内外导体的电流强度均为i,方向相反。则由安培环路定律可知,在图1半径为ρ的圆周上磁感应强度B的分布为
(17)
则穿过半径为ρ,宽度为dρ的圆环的磁链dψ为
(18)
于是可求得穿过介质总的磁链,也是同内导体电流的交链
(19)
从而由电感的定义式可求得分布电感
(20)
将式(16)和式(20)代入式(13),并注意到ε=ε0εr,μ=μ0μr,μr≈1(大多数通用媒质都满足此条件),所以,同轴特性阻抗为
此结果和利用场论推导的结果(见式(9))完全一致。
2 实验设置与验证
2.1 实验设置
设置了4组同轴线实验,如表1所示。为方便比较,理论值和仿真值并列放置。表中前3个参数,即同轴线结构尺寸a和b值以及相对介电常数εr都是可以改变的。这3个参数每改变1个,就是对应1条新的同轴线。此表格建议在Excel软件环境下建立,并将理论值按照相应公式编辑好,这样表中前3个物理参数(a、b和εr)每改变1次,相对应的特性参数(C、L和Z0)理论值就能及时反应出来,无需重复人工计算。同样特性阻抗的计算值,按相应仿真值编辑好公式,这样将每次分布参数的仿真结果填入表格后,特性阻抗的计算值也会自动算出。
表1中仿真值是用电磁场仿真软件实现的,采用的是ANSYS Maxwell v16来完成的。
2.2 分布电容仿真
分布电容的仿真可用二维静态场求解。首先,在ANSYS Maxwell v16中建立二维同轴线模型如图3所示,求解类型选择“Electrostatic”,由于是无耗理想传输线,所以内外导体设置为理想导体,介质材料不考虑损耗。建议将结构参数(a和b)和介质参数(εr和μr)全部参数化,这样就无需重复建模了,只需改变参数值就可以生成新的模型;然后给模型添加激励,这里选择给内外导体加电压值;接着指定求解区域,初始化网格而后运行仿真就可以了;最后,观察仿真结果。ANSYS Maxwell v16可以观察到各种场结构,但这里仅给出电通量密度的标量和矢量分布图,如图3(a)和(b)所示,就是表1中第1组同轴线数据的仿真结果。通过对电通量密度场D分布的观察可以发现其场结构是符合理论分析的。图3(c)为分布电容值的观察界面,其分布电容值为80.278 pF/m。其他3组同轴线分布电容仿真值见表1。
2.3 分布电感仿真
将求解类型设置为静磁场类型“Megnetostatic”,激励条件改为内导体加电流源,外边界即外导体的内壁磁矢位A设置为0,然后求解仿真即可。求解后同样可以观察各种场结构的分布。表1中第1组同轴线仿真结果如图4所示。这里仅给出磁感应强度的标量和矢量分布情况,分别如图4(a)和(b)所示,分布电感值为138.59 nH/m,如图4(c)所示。其他3组同轴线分布电感仿真值见表1所示。

表1 同轴线分参数

(a)电通量密度D标量分布
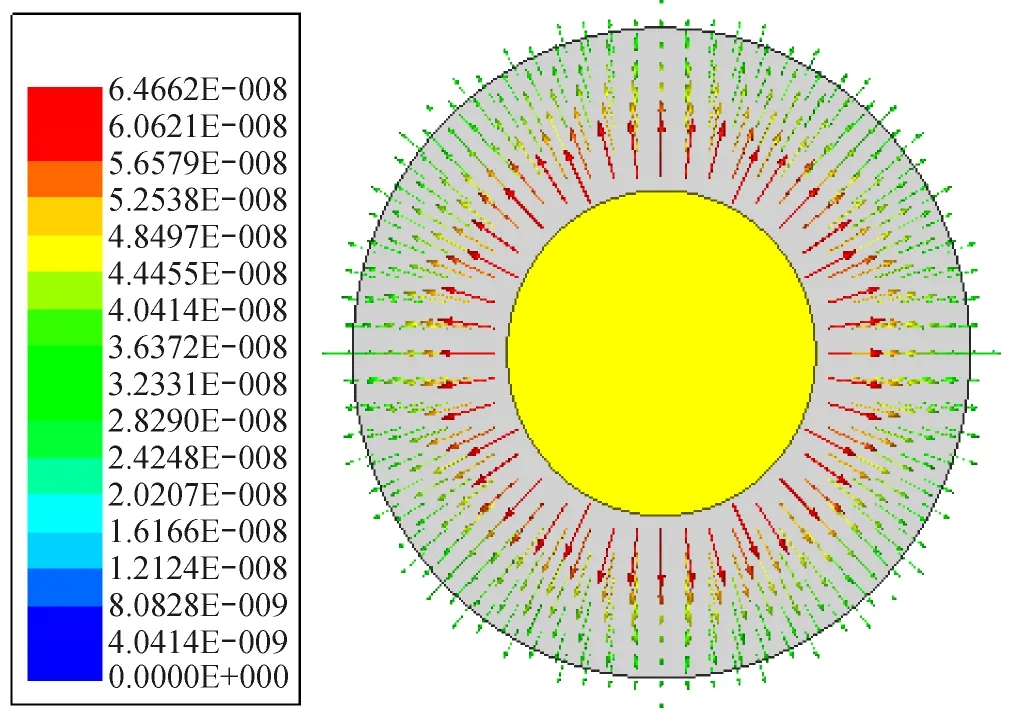
(b)电通量密度D矢量分布
2.4 特性阻抗计算
按照2.2节和2.3节的仿真方法可以仿真出其他各组同轴线的分布电容值C和分布电感值L,将其代入到表1相应位置中,特性阻抗值Z0就可以自动算出,其结果如表1所示。
通过表1各组特性阻抗计算结果对比,很容易发现其中规律:① 在其他参数不变的情况下,特性阻抗随b/a比值增大而增大。② 在其他参数不变的情况下,随材料介电常数增大而减小。这两个规律在射频与微波电路分析中是非常有用的。

(a)磁感应强度B标量分布

(b)磁感应强度B矢量分布

(c)分布电感L
3 结 语
从场和“路”两方面对传输线特性阻抗的求解进行了理论分析与比较,而后根据所得结论,构建了计算特性阻抗的实验方案,并用静态电磁场理论推导了无耗同轴传输线的分布电容和分布电感的表达式。最终借助ANSYS Maxwell v16不仅完成了分布电容、分布电感和特性阻抗的计算,还观察了传输线内部电通量密度和磁感应强度这两种场结构的分布状态。本次实验成功地将均匀平面波传播理论、传输线理论、静态电场理论和静态磁场理论融合到实践当中,揭露了特性阻抗本质与表象的关系。因此,本实验是对所学电磁场与电磁波相关理论的一个综合应用,本实验方法可以推广到任何已知和未知的TEM波传输线特性阻抗计算中去。
本次实验将理论值与仿真实验全部放在同一张Excel表格中完成设置,特别有利于比较和总结规律。
