对LLE图像超分辨率算法的几个改进
2019-12-19侯志明高阳洪明月
侯志明 高阳 洪明月


摘 要: 本文旨在对一种经典的图像超分辨率方法——LLE算法(局部线性嵌入算法)及其代码进行一些改进和优化。为提高对大量图像块的搜索速度,我们采用kd树算法整理样本集;鉴于像素点灰度值的非负性,我们采用非负最小二乘法而不是LLE原来的最小二乘法,确定低分辨率图像块与训练样本集中k最邻近图像块的回归系数;最后,考虑到样本集选取和变换会对实验结果造成影响,我们对训练样本图像的若干因素进行一系列组合,通过正交实验设计得出样本集的最佳选取标准。实验表明,改进后的LLE图像超分辨率算法相比传统的图像插值算法和原LLE算法,效果有较大的改进。
关键词: 图像超分辨率;LLE算法;kd树;非负最小二乘法;正交实验设计
【Abstract】: This paper concerns of the improvement and optimization of the code of a classical example based single image super-resolution method: LLE algorithm(locally linear embedding algorithm). For improving the speed of searching large amount of image patches, we employ the kd-tree algorithm to the example patches of training set; furthermore instead of employing the least square regression method, we apply non-negative version of it to obtain the regression coefficients, based on the factor that the non-negative of pixel gray values of image; at last, considering the important effect of the selection and translation of examples on the results of super-resolution methods, we employ the orthogonal test design to some factors of image affine translation for example selection of training set. Experiments demonstrated that our new LLE algorithm can improve the performance greatly, comparing to conventional image interpolation methods and the original LLE method.
【Key words】: Image super-resolution; LLE algorithm; Kd-tree; Non-negative least square; Orthogonal test design
0 引言
給定一幅低分辨率的图像,图像超分辨率的目的是重建一幅与其对应的高分辨率图像[1]。是图像处理[2-6]的一种重要技术。图像超分辨率算法主要有三种类型:基于插值的算法;基于重构的算法;基于样本学习的算法。LLE(局部线性嵌入)是一种经典的基于样本学习的图像超分辨率方法[7]。它假定图像低分辨率块所处的低分辨率流形和相应的图像高分辨率块所处的高分辨率流形有类似的几何特征和结构[8]。基于此假定,LLE首先进行样本集的训低分辨率图像块,并将待提升分辨率图像块用其k近邻线性表示,得到表示系数。然后将表示系数应用到k近邻相应的k个高分辨率图像块上,从而得到待提升分辨率低分辨率图像块相应的高分辨率图像块。LLE思路简单,超分辨率效果好,因此经常被为超分辨设计的新算法作为比较对象,具有广泛的应用。
本文旨在对LLE进行几个改进,以优化它的代码质量,提升其效果。
在寻找低分辨率图像块k最邻近过程中,随着样本集图像的不断增多,图像块的数目急剧增多,原始k邻近搜索算法需要计算样本集中每个低分辨率图像块与待提升分辨率图像块的距离,然后排序,因而耗费时间急剧增加。并且这些距离计算和排序都是在线进行,因此也增加了超分辨率的时间。分析样本集的数据特征,其实例数远远大于样本维数,符合kd树数据特征[9],因而采用kd树算法对样本集进行离线构建,在提升一幅图像的分辨率过程中只需要对kd树进行在线索检,这可以大大提高超分辨率的速度。
此外,LLE算法求解线性表示系数时用的是原始的最小二乘回归法,因为图像灰度值范围必须非负,我们优化它为约束最小二乘法[10],利用非负最小二乘实现这一过程[11]。
最后,经验表明样本集的选取对超分辨率效果会造成很大的影响。为探索最优的样本选取标准,我们利用一种正交实验设计方法——综合平衡法对样本来源、是否进行旋转以及图片放缩尺寸等因素进行进一步分析,从而找出最佳状态的水平组合[12]。
综上,我们主要做了如下三处改进:样本集的存储与搜索采用kd树算法、回归系数使用非负最小二乘法求解、样本集来源进行多层筛选。
实验结果表明,通过以上的改进和优化,LLE算法的性能有较大的提升。
下面我们分别对现有LLE图像超分辨率算法的基本理论,以及我们对算法的改进进行具体说明,并在文章末尾得出最优化的样本集选取方案。
1 LLE图像超分辨率算法的基本理论
将低分辨率的图像作为待提升分辨率的输入图像,我们通过训练一幅甚至多于一幅的低分辨率图像以及对应的高分辨率图像来估计目标高分辨率图像。每个低分辨率图像及对应的高清晰度的图像表示为一组小的重叠图像补丁。和有相同数目的补丁,中每个低分辨率的补丁以及对应的在中高分辨率的补丁数目也相同。针对,以及,相应分别对应的的补丁集设为,,,。
根据LLE算法基于图像块流形的假定,我们希望我们的方法具有以下属性:中的每个补丁都与从训练集中得到的多个小补丁转换相关联,同时相邻的补丁通过重叠来限制从而加强局部兼容性和平滑性。特别的,在处理重叠补丁时,我们采用均值对其进行估计,代替部分数值结果。最后我们可以得到结合kd树以及非负最小二乘算法得到的超分辨结果。
为了对图像超分辨率重建的结果进行质量评价,基于S-CIELAB色差模型提出的色差公式,计算均方误根以及峰值信噪比。
其中分别为图像行、列像素数,和分别为待比较图像和比较图像在位置的灰度值,通常是图像的灰度级。
2 kd树选取最邻近样本集
kd树适用于训练实例数远大于空间维数时的k近邻搜索。该算法采用一定的标准对k维空间的每一维进行二分。构造kd树相当于不断地用垂直于坐标轴的超平面对k维空间进行二分,从而形成一系列的k维超矩形区域,其中每一个节点对应一个k维超矩形区域。随后基于划分好的区域,通过目标点与划分标准之间的比较缩小搜索区域,进而大大提高搜索效率。
2.1 建树过程
为直观说明kd树分割区域的思想,以二维数据7个样本点为例,首先以建树为基础给出建树的示意图,如图1所示。
根据图1所示二叉树,对7个样本点每一维求方差,方差最大一维的列向量找到中位数,该列数据与中位数大小进行比较,划分7个点为根节点(中位数所在点)、左子树(对应列大于中位数点)、右子树(其余点),遵循建树过程对2维平面逐步二分,最终将7个点建成kd树。其中点A、B、C为分割点,根节点A对X维划分,子树根节点B、C对Y维划分,图2为空间的分割面分割图。
2.2 搜索过程
从根节点开始,循环下列操作:
Step1当前点未被标记时执行以下循环:
(1)求其与目标点欧式距离,标记该点,若距离小于第k个近邻点与目标点距离则更新k近邻点;
(2)比较目标点与当前点划分子树维度数值大小,如果对应一边不存在子树则停止循环,否则将对应一边子树的根节点作为当前点。
Step2如果当前点为根节点则结束循环,否则执行以下操作:
(1)计算目标点与当前点父节点对应划分维度的数值间距离;
(2)若该距离大于第k近邻距离数值,则考虑当前点父节点是否存在另一子节点;
(3)若存在则令其为当前点,否则令当前点父节点为当前点。
下面根据上述过程对前面7个点对搜索点进行最搜索(k近邻搜索过程类似)。
2.2.1 确定搜索路径
(1)计算目标点到根节点A的距离并更新当前最小距离的点为A;图3为目标点距离更新示意图。
(2)当目标点比A所指分割维度数值小,移动当前点至A的左子节点B;如图4所示。
(3)重复(1)(2)直至当前点为叶子节点,即当前点移至E,因此当前搜索路径为A→B→E。图5为叶子节点和搜索路径的确定示意图。
2.2.2 回溯至根节点
(1)由于目标点到当前点E的父节点B分割面
的距离大于最小距离,故无需搜索B的另一子节点D所在区域,故令当前点父节点B为当前点;图6为搜索区域和父节点的确定示意图。
(2)以目标点为圆心最近距离为半径的圆,越过当前点B的父节点A所在分割面,故需要搜索A的另一子节点C所在区域,重新确定搜索路径为C→G,更新最小距离;如图7所示。
(3)重新向上回溯,由于目標点到当前点G的父节点C的分割面的距离小于最小距离,故需要搜索C的另一子节点F所在区域,令当前点为F,更新最小距离;图8为搜索路径的重新回溯。
(4)回溯至父节点C,令当前点为C,更新最小距离;如图9所示。
(5)由于C的父节点A的另一子节点B所在
区域已被标记,故直接回溯至根节点A,更新最小距离搜索结束。最终得到点即为A最近邻点。如图10所示。
3 非负最小二乘法确定k近邻回归系数
在kd树搜索算法得到k最邻近样本集的基础上,计算目标函数的最佳重构造权重,将所得的最佳重构造权重用于计算代表目标图像的数值,其目标图像的数值为正,因此在求权重系数时,所求的线性方程组的解出现负数是没有意义的。虽然方程组可能得到精确解,但却不能取负值解。如果所求的权重系数为负值,在这种情况下, 其非负最小二乘解比方程的精确解更有意义。下面我们首先利用传统的最小二乘法求解权重系数,这就要求解下面的优化问题:
4 样本集选取优化
为了追求较高的样本分辨率,检测我们实验的结果,不妨假设已有大的分辨率较高的目标图像A,随后将A缩小二倍得到输入的小图样本A,然后针对小图样本集A进行样本集的筛选,最后利用LLE算法进行超分辨率重建,将得到的结果与图像A得到的结果的信噪比进行对比,旨在筛选出最好的样本搜索方案。
4.1 样本来源分析
考虑到LLE算法需要构建训练的样本集,我们选取5幅作为A的小图样本集图像输入如图11所示。
分别以单幅图像形式与累加图像形式训练这5个样本集,分别测得PSNR如表1所示。
根据实验结果我们可以看到,在提高信噪比为主要目的的前提下,所有LLE算法得出结果好于插值法得到结果,同时选用自身为样本训练集的实验效果明显优于搜索其他训练样本得到的结果。随着样本集个数的增加,信噪比虽逐渐接近自身为样本集的效果,甚至当累计5幅图像时已经略微超过其大小,但时间上却高了一倍之多。综上分析,选用待放大图像自身进行样本集扩充可快速达到较好的效果。
4.2 插值法对比分析
为了进一步说明用自身图像信息作为样本与插值法对比效果,我们随机筛选五幅图片进行超分辨率重建,分别采用LLE算法以及插值法进行实验。
对于LLE算法,我们对A利用插值法进行放缩得到A、1/2 A、2 A,分别作为样本集,随后利用LLE算法进行超分辨率重建,分别测得PSNR如表2所示。
因此根据上述结果,分别以自身图片信息A或2A作为样本训练得到PSNR平均分别比插值法高0.58466、0.39396,均优于传统插值法的效果。而以1/2 A为样本却平均比插值法低0.2366,可见对A放缩后再作为样本集会对图像信息造成一定损失,因而直接选取A本身作为样本集进行训练的效果,会稳定且明显的好于插值法。
4.3 正交实验确定最佳组合水平
考虑到训练样本的效率以及质量直接影响到超分辨率图像重建的效率以及清晰程度,因此根据主要影响样本集训练导致分辨率重建性能优劣的3个因素,即训练样本的来源、是否对样本集进行镜像旋转以及筛选好样本后是否进行放缩进行分析。
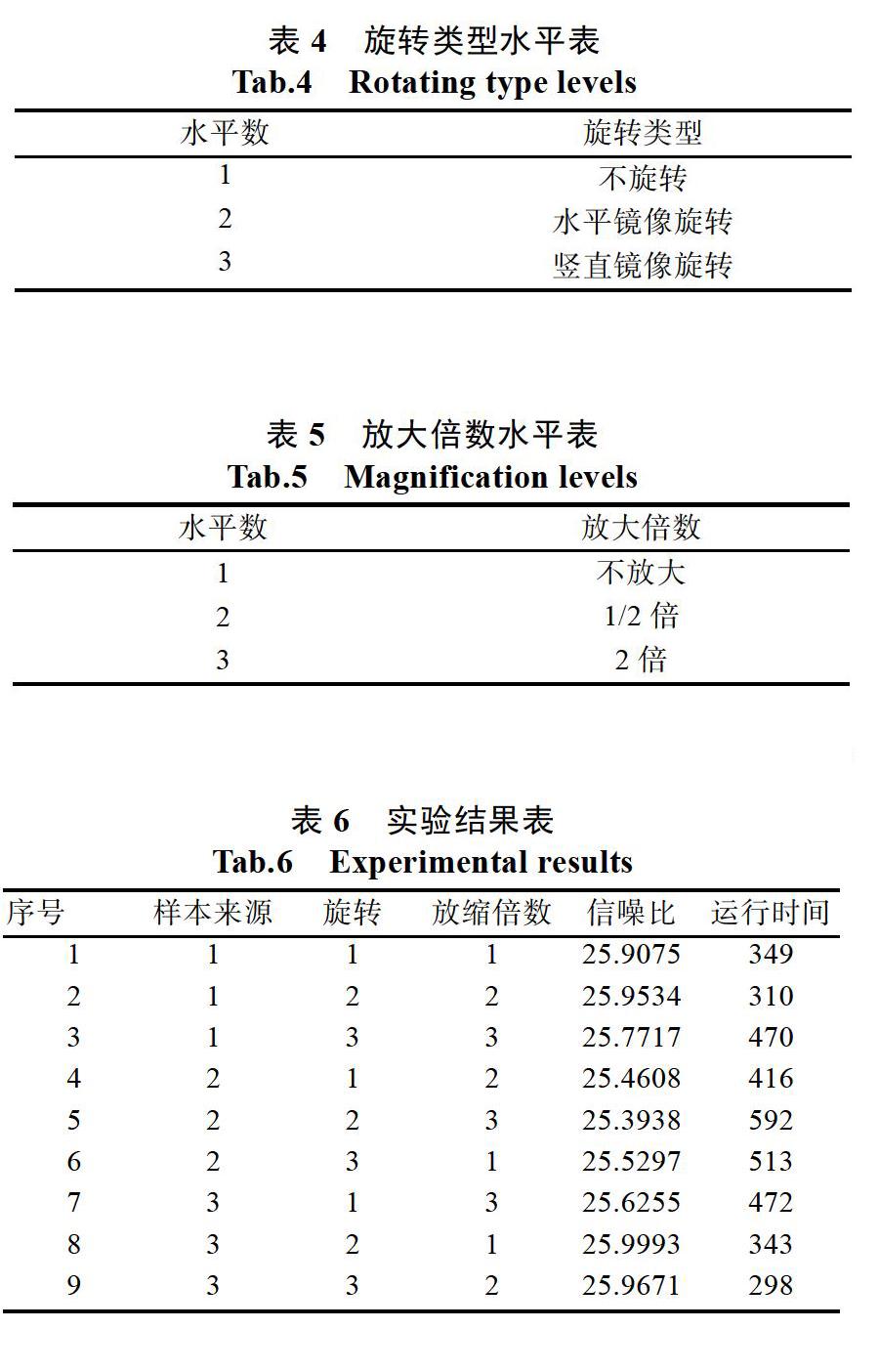
本文采用正交实验设计的方法,针对目标图像的信噪比以及运行时间,利用三因素三水平正交实验表进行实验设计。考虑到不同因素水平数较多,且一般情况下个水平交互作用的影响较弱,因此在不考虑交互作用的前提下进行正交实验设计。
首先考虑第一个因素即样本是否来自于自身信息扩增以及是否来自于随机搜索,由于只有两个水平我们采取虚拟水平的方法,根据样本来源分析部分得到的结论我们可以看到,对自身进行样本扩充的效果优于随机搜索,因此我们将其作为第三水平。如表3所示。
随后根据实验设计的方法,通过求解各水平对应的平均水平,我们可以得到以信噪比为最优方案的参数组合为1,2,1,即将自身图像加上自身水平旋转图像作为样本效果最好。考虑到第三水平恰好为第一水平,因此正交实验表中的第8组恰好为该组合,其PSNR为25.9993比插值法要高出0.6371。得到超分辨率图像如图14所示。
综上所述,在训练样本集时选取自身图片信息加以旋转,在此基础上扩充样本集可以较好的提高信噪比。
5 结论与展望
为改进LLE算法的性能,我们利用kd树搜索,以加快在训练大规模样本时找到最近邻的图像补丁。同时考虑图像信息特点,利用非负最小二乘进行超分辨率重建,化简算法流程。最后在改进后的算法基础上引入实验设计的思想,给出训练模型时较好的样本集筛选组合方案,为进一步提升图像的信噪比提供可能。今后的工作聚焦于利用集群计算或云计算的工具在更大规模训练图像集上验证和提升算法的性能,并寻求算法在遥感图像处理[8]等方面的应用。
参考文献
[1]Jianchao Yang, John Wright, Thomas S. Huang, Yi Ma. Image Super-Resolution Via Sparse Representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 19(11): 2861-2873.
[2]尹宗天, 谢超逸, 刘苏宜, 等. 低分辨率图像的细节还原[J]. 软件, 2018, 39(5): 199-202.
[3]刘鑫淼, 康朝红, 薛乐乐. 基于ICA 的遥感图像去噪融合研究[J]. 软件, 2015, 36(7): 53-56.
[4]谢佩军. 基于复Contourlet 和各向异性扩散的图像降噪算法[J]. 软件, 2016, 37(4): 35-39.
[5]曹妍, 陈伟, 徐森. 图像去噪方法研究与仿真[J]. 软件, 2015, 36(4): 33-36.
[6]宋婷婷, 徐世许. 基于全采样和 L1 范数降采样的卷积神经网络图像分类方法[J]. 软件, 2018, 39(2): 75-80.
[7]HongChang, Dit-Yan Yeung, Yimin Xiong. Super-Resolution Through Neighbor Embedding[J]. IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Department of Computer Science. Hong Kong University of Science and Technology. Clear Water Bay, Kowloon, Hong Kong. 1063-6919/04.2004. pp: 1063-6919.
[8]Huihui Song, Bo Huang. Spatiotemporal Satellite Image Fusion Through One-Pair Image Learing[J]. IEEE Transactions on Geoscience and Remote Sensing. VOL. 51, NO. 4, APRIL 2013. pp: 1883-1896.
[9]張蓬郁, 王煜, 江旻宇, 邵嘉琳, 等. 基于K-D树和机器学习的时空数据检索-预测系统[J]. 软件, 2018, 39(08): 215-218.
[10]杨幸彬, 吕京国, 张丹璐,等. Dense SIFT与改进最小二乘匹配结合的倾斜航空影像匹配方法[J]. 测绘通报, 2018(10): 32-36+70.
[11]齐永锋, 杨乐, 火元莲. 基于稀疏非负最小二乘编码的高光谱遥感数据分类方法[J]. 农业机械学报, 2016, 47(07): 332-337.
[12]张东明, 张晓云, 杨小波, 等. 基于正交实验和多项式回归分析方法的非典型接触状态车人碰撞事故参数分析[J]. 上海交通大学学报, 2019, 53(01): 55-61.
