基于改进GM(1,1)和SVM的轨道电路故障最优组合预测模型研究

黄斌

基于改进GM(1,1)和SVM的轨道电路故障最优组合预测模型研究

黄斌

(柳州铁道职业技术学院，广西 柳州 545616)

针对传统电务部门对ZPW-2000A型轨道电路维护中所沿用的“故障修”及“定时修”在保证行车安全、提高运营效率及经济性等方面的不足，采用改进GM(1,1)和支持向量机(SVM)模型进行最优化权重组合，对轨道电路进行故障预测。首先，对GM(1,1)模型进行滑动平均法改进，将已知轨道电路的状态序列分别送入改进GM(1,1)和SVM模型进行序列预测。其次，分别对2种预测算法进行最优组合。最后，以2个案例进行模型的测试，验证了组合模型方法的可行性与有效性。

轨道电路；改进GM(1,1)模型；支持向量机；故障预测

ZPW-2000A型无绝缘移频自动闭塞轨道电路是我国铁路信号系统中应用十分广泛的重要基础设备[1−2]。目前，电务部门对轨道电路的检修方式[3]主要有：1) 结合CD96-3型轨道电路测试仪的各电压测试值与标调表比对判断；2) 借助微机监测记录的各电压日曲线、日报表分析，一般故障下参数电压波动或直接降为0。长期以来，轨道电路面临着“期望设备高性能的运转与维护资源的有限”的矛盾。我国铁路轨道电路仍然沿用传统的“定时修”和“故障修”策略，即在固定的时间或当设备发生故障后才进行检测维护，此方法存在维护效率低、故障隐患高的缺点，若未及时处理故障很可能造成行车事故，影响行车效率。目前，针对轨道电路的主要研究有：ZHAO等[4]提出轨道电路补偿电容的快速故障诊断数学模型，实现故障实时监测。杨世武等[5]给出一种基于神经网络的轨道电路混合故障诊断算法，旨在通过快速的神经网络训练，实现轨道电路故障诊断的高效性。LIU等[6−8]分别针对轨道电路的故障采用智能算法进行优化诊断研究。伴随着3C(计算机、通信和控制)技术及故障预测与健康管理(Prognostic and Health Management, PHM)[9]技术的发展，智能交通系统(Intelligent Transportation System,ITS)同样快速发展，图1为铁路智能运维架构。宁滨[10]指出，目前铁路设备采用基于静态数据的检修维护难以满足交通系统安全保障及较低的运营成本，提出宜结合系统运行机理建立基于“状态修”的智能维护模式，此也是当前ITS的核心课题。将智能化的预测技术引入轨道电路的故障分析中，对于保证列车行车的RAMS(可靠性、可用性、可维护性和安全性)技术意义重大。

图1 设备智能运维架构

故障预测作为一类新兴学科，旨在对设备进行状态监测，提前获悉运行状态[11]。首先，ZPW-2000A型轨道电路结构复杂且状态退化过程单调，可获特征参量有限。其次，传统GM(1,1)模型主要解决“贫信息”、“少数据”和“不确定性”的问题。为避免GM(1,1)模型在预测中忽略系统发展过程的一些必要干扰因素、影响预测精度，本文对其改进优化。鉴于传统单一故障预测精度低的缺点，引入组合预测方法。结合支持向量机(SVM)在解决小样本、非线性和高维数据模型中泛化能力强的优势，选择改进GM(1,1)与SVM模型进行最优化组合，实现ZPW-2000A故障预测。本文旨在为电务人员掌握轨道状态、辅助故障分析和故障处理起到指导作用。

1 ZPW-2000A轨道电路原理结构

ZPW-2000A型轨道电路是在法国UM-71的基础上发展而来的。设备一般分为室内和室外设备2部分[12]，如图2所示。

图2 轨道电路主体结构划分

轨道电路的主要作用在于监测线路空闲和占用状态。若钢轨有车占用，列车轮对的分路作用会导致信号接收器电压降低。ZPW-2000A型轨道电路发送器将电信号通过铁路线路传送到信号接收端，信号传输过程如图3所示。

图3 轨道电路信息传输

2 组合算法介绍

2.1 GM(1,1)模型

传统GM(1,1)为包含单变量的一阶灰微分方程。其基本思路是：将无规则的原始数据进行累加生成规律性强的数列重新建模，由新生成数据再累减得到还原模型，再由还原模型进行预测[13]，其建模过程如下。

Step 1：生成一次累加模型

Step 2：构造背景值

对(1)做紧邻均值生成计算，结果为GM(1,1)模型背景值，记做(1)：

其中：2,3,…,。

则：

为GM(1,1)的灰色微分方程。

Step 3：建立GM(1,1)模型

对生成序列(1)做一阶单变量微分方程拟合，得到灰色白化过程的动态模型为：

其中：为发展系数；为灰作用系数。

结合最小二乘法得到：

可计算得白化方程的解为:

Step 4：累减生成

由一次累减生成得到还原数列为：

Step 5：求出绝对误差和相对误差，最终利用该序列进行预测。

2.2 改进GM(1,1)模型

若对于2个端点，改进过程为：

其中，′(0)为紧凑平滑处理后的值。通过增加数据的权值，避免数据过度波动。

2.3 SVM算法

采用不敏感损失函数控制模型的拟合度，影响模型的个数及训练模型泛化能力。越大，训练模型的个数越小，预测精度越低；越小，回归模型精度提高，训练个数增多：

其中：为模型理想输出。

通过引入惩罚因子和松弛因子λ和λ*， 满足：

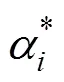
结合式(13)和式( 14)，在式(13)的约束下问题可转换为求如式(16)所示函数的最大值：

将式(15)代入式(11)得到回归模型，如式(17):

选择核函数(x,x)替代内积计算，得到回归模型为：

其中：(x,x)选择常用的高斯核函数；为核宽度，与样本空间成正比。

2.4 最优权重

按照组合预测理论的权重计算方法，由二次规划寻优可建立组合预测模型。结合2种算法的故障预测误差可确定误差函数，以实现预测误差平方和值为约束条件，构造最优组合模型。计算对应的最优权重。

结合改进GM(1,1)及SVM 2种预测算法，x()为第2种预测算法分别在时刻的预测值，则第个预测方法在时刻的预测误差及相应的预测误差信息矩阵表示为：

将2个预测结果进行不等权重组合，令[1,2,…,w]T为各个预测方法对应输出的权重值，其综合预测结果为：

以误差平方和最小为约束项，通过求解二次规划模型来确定最优权重：

通过引入Lagrange乘子，得式(24)：

分别对和求导：

可得权重为：

3 预测结果验证方法

1) 相对误差

2) 样本均方误差

3) 平均绝对误差

个预测误差的平均绝对值，记为：

其值越小，预测准确度越高。其中为外推数据个数。

平均相对百分误差

个预测误差的平均相对百分误差，记为：

其值越小越好。

4 算例分析

4.1 模型验证

采用本方法提出的改进GM(1,1)和SVM优化组合方法。本文的测试平台为：PC终端，WINDOWS7 32位操作系统，处理器：Intel(R) Core3，MATLAB2014b。

本文数据来自于南宁某客运站微机监测系统采集的区间轨道电路信息。鉴于数据的庞大，对轨道电路预测数据进行筛选，选择开天窗定期现场测试的信号设备台账。

结合2016年2月~2018年3月的轨出1的电压作为训练模型。2018年4月~2018年7月的作为测试模型。仿真模型数据来自柳州某客运站每月1次的维修测试，内容及数据如表2所示。为尽可能提高模型的泛化能力，SVM模型的参数取值分别为：0.02,162,1.49。原始预测数据如表1所示，各种算法预测结果如图4所示。

表1 测试数据实际输出

图4 轨出1预测输出值

表2通过对图4中5种预测算法性能结果进行比对，明显可以看出最优组合预测结果与现场实际值拟合度更高，验证了组合模型预测的高效性。

表2 各种方法性能比较

4.2 预测实例验证

参考文献[11]所述的事故发生在2000年10月底，某局发生的钢轨电气式断轨，由于轨道电路得不到检查，造成列车脱轨的严重事故。若可以提前进行故障预测，则可避免事故发生。分离式断轨的表现为本区段红光带：轨出1的电压值小于落下门限值(170 mV)。

其中，2000年2月~9月的原始数据为：(0)={650, 595, 301, 450, 470, 370, 200, 166}得到各个算法性能参数对比如表3所示,序列数=9。

对于改进GM(1,1)模型，模型系数=−0.009 6，=72.473。对于2月份的数据可按式(8)计算，3月份输出值按式(9)可获得。

对于其他时间的预测输出预测同样按照式(9)可获得。

在SVM模型中，模型参数设置为：0.04,167,1.51结合式(18)逐次循环计算。最后将2种方法分别获得的预测序列按2.4的最优组合方法结合。各类方法预测结果及性能比较如表3所示。

表3 各种方法性能比较

从表3可以看出，组合预测模型在5个预测模型中的相对误差和平均相对误差均最小，验证了预测精度的高效性。为直观起见，在MATLAB2014b平台上进行仿真，得到结果如图5所示。

图5 多预测方法对比效果

5 结论

1) ZPW-2000A型轨道电路是铁路信号系统中重要的基础设备，对其进行故障预测的研究意义重大。鉴于单一预测方法预测精度不高的特点，本文结合对象故障发生的随机性与模糊性以及可获悉的样本较少的特点，提出采用改进GM(1,1)与SVM进行轨道电路的最优组合故障预测模型，综合了2种模型的各自优点。

2) 通过2个实例进行多个算法各项参数的对比验证，均证明了组合预测模型的高效性。

3) 本文为轨道电路提供了一种故障预测与维修的新方法。

[1] 王瑞峰. 铁路信号运营基础[M]. 北京: 中国铁道出版社, 2008. WANG Ruifeng. Basis of railway signal operation[M]. Beijing: China Railway Press, 2008.

[2] 徐侃, 赵林海. 无绝缘轨道电路补偿电容多故障的快速诊断方法[J]. 铁道学报, 2018, 40(2): 67−72. XU Kan, ZHAO Linhai. A rapid diagnosis method for multi-fault compensation capacitance of non-insulated track circuit[J]. Journal of the China Railway Society, 2018, 40(2): 67−72.

[3] 董昱, 陈星. 基于粗糙集和模糊认知图的 ZPW-2000轨道电路故障诊断[J]. 铁道学报, 2018, 40(6): 83−89. DONG Yu, CHEN Xing. Fault diagnosis of ZPW-2000 track circuit based on rough set and fuzzy cognitive map [J]. Journal of the China Railway Society, 2018, 40(6): 83−89.

[4] ZHAO Linhai. Fault diagnosis for track circuit using AOK-TFRs and AGA[J]. Control Engineering Practice, 2012, 20(12): 1270−1280.

[5] 杨世武, 魏学业, 范博. 基于数据的轨道电路故障诊断的混合算法[J]. 北京交通大学学报, 2012, 36(2): 40−46. YANG Shiwu, WEI Xueye, FAN Bo. A hybrid algorithm for track circuit fault diagnosis based on data[J]. Journal of Beijing Jiaotong University, 2012, 36(2): 40−46.

[6] LIU Linhui, YANG Minyuan. Simulation calculation about interference of geomagnetic storms on track circuit equipment[J]. Journal of the China Railway Society, 2015, 37(8): 48−52.

[7] 张友鹏, 常高武, 赵斌. 基于SA算法的无绝缘轨道电路故障综合检测方法[J]. 铁道学报, 2017, 39(4): 68− 72. ZHANG Youpeng, CHANG Gaowu, ZHAO Bin. Comprehensive fault detection method of non-insulated track circuit based on SA algorithm[J]. Journal of the China Railway Society, 2017, 39(4): 68−72.

[8] 陈星, 董昱. 基于模糊认知图模型的轨道电路故障诊断[J]. 铁道科学与工程学报, 2017, 14(9): 1983−1989. CHEN Xing, DONG Yu. Fault diagnosis of track circuit based on fuzzy cognitive map model[J]. Journal of Railway Science and Engineering, 2017, 14(9): 1983−1989.

[9] 戴乾军, 陈永刚, 陶荣杰. 基于动态PSO优化HSMM的转辙机PHM模型研究[J]. 铁道标准设计, 2018(9): 174−178. DAI Qianjun, CHEN Yonggang, TAO Rongjie. Research on PHM model of switch machine based on dynamic PSO optimization HSMM[J]. Railway Standard Design, 2018(9):174−178.

[10] 宁滨. 智能交通中的若干科学和技术问题[J]. 中国科学, 2018, 48(9): 1264−1269. NING Bin. Some scientific and technical problems in intelligent transportation[J]. China Science, 2018, 48(9): 1264−1269.

[11] Sharma D, Chandra P. Software fault prediction using machine-learning techniques[J]. Smart Computing and Informatics, 2018, 10(1): 978−981.

[12] WU Xiaochun, JI Guanggang. Research on a kind of protective choke matching transformer for track circuit[J]. Journal of Applied Science and Engineering, 2018, 21(3): 124−128.

[13] 汤旻安, 李滢. 灰色系统理论在地铁轮对踏面磨损预测中的应用[J]. 铁道学报, 2014, 36(12): 35−39. TANG Minan, LI Ying. Application of grey system theory in the prediction of tread wear of metro wheel sets [J]. Journal of the China Railway Society, 2014, 36(12): 35−39.

[14] DAI Su, NIU Ding. Forecasting of energy-related CO2emissions in China based on GM(1,1) and least squares support vector machine optimized by modified shuffled frog leaping algorithm for sustainability[J]. Sustainability, 2018, 10(4): 958−960.

Research on fault optimal combination prediction model of ZPW-2000A track circuit based on improved metabolic GM(1,1) and SVM

HUANG Bin

(Liuzhou Railway Vocational and Technical College, Liuzhou 545616, China)

In view of the shortcomings of the “fault repair” and “timing repair” used by the traditional electrical department in the maintenance of ZPW-2000A track circuit in ensuring traffic safety, improving operation efficiency and economy. This paper adopted the improved GM(1,1) and support vector machine (SVM) model to carry out the optimal weight combination for the fault prediction of track circuit. Firstly, the GM(1,1) model was modified by the sliding average method, and the known state sequence of the track circuit was fed into the improved GM(1,1) and SVM models for sequence prediction. Secondly, the optimal combination of the two prediction algorithms was build. Finally, two cases were used to test the model to verify the feasibility and effectiveness of the combined model method.

track circuit; improved GM(1,1); SVM; fault prediction

U283.2

A

1672 − 7029(2019)11− 2852 − 07

10.19713/j.cnki.43−1423/u.2019.11.026

2019−02−20

广西高校中青年教师基础能力提升项目(2017KY1239)；广西高等学校千名中青年骨干教师培育计划资助项目；广西高等学校高水平创新团队及卓越学者计划

黄斌(1983−)，男，河南南阳人，副教授，从事轨道交通信号与控制研究；E−mail：huangbinliutie@sina.com

(编辑 阳丽霞)