透过教材看“加权平均数”

余旭红

苏科版《数学》九年级上册第三章第一节“平均数”（100 ～101页）的问题2是这样描述的：

某电视台要招聘1名记者，甲、乙、丙三人应聘参加了3项素质测试，成绩如下（单位：分）：

[ 甲 乙 丙 采訪写作 70 90 60 计算机操作 60 75 84 创意设计 86 51 78 ]

如果采访写作、计算机操作和创意设计的成绩按5∶2∶3计算，那么哪个人的素质测试平均成绩最高？

【问题解析】甲、乙、丙三人的素质测试平均成绩不仅与采访写作、计算机操作及创意设计的成绩有关，而且和三项素质测试的重要程度有关。采访写作、计算机操作及创意设计的成绩按5∶2∶3计算，说明采访写作、计算机操作及创意设计的“重要程度”不一样，它们在总成绩中各占[55+2+3]、[25+2+3]、[35+2+3]，因此不难得到甲的得分=70×[55+2+3]+60×[25+2+3]+86×[35+2+3]=72.8（分）;同理可得乙、丙的得分。

【概念链接】一组数据的平均数，不仅与这组数据中各个数据的值有关，而且与各个数据的“重要程度”有关。衡量各个数据的“重要程度”的数值叫做权。问题2中甲的得分72.8是数70、60、86按5∶2∶3计算所得的“加权平均数”。

加权平均数的解题应用有很多，现对典型问题进行列举，和同学们一起交流探讨。

典型应用一：从统计表中收集数据，求加权平均数

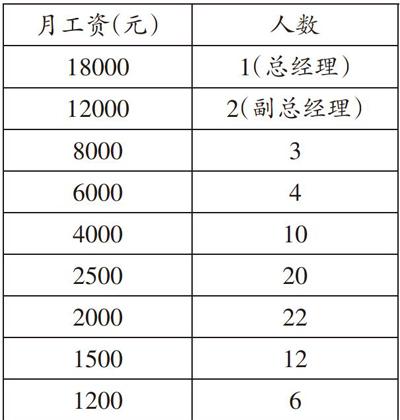
例1 某公司全体职工的月工资如下：

[月工资（元） 人数 18000 1（总经理） 12000 2（副总经理） 8000 3 6000 4 4000 10 2500 20 2000 22 1500 12 1200 6 ]

求这个公司全体职工的月平均工资，并说明能否用月平均工资表示该公司员工收入的“平均水平”。

【解析】从统计表收集数据，可得各类月工资对应的人数，即各类月工资相应的权数，从而可得这个公司全体职工的月平均工资=[180]（18000×1+12000×2+8000×3+6000×4+4000×10+2500×20+2000×22+1500×12+1200×6）=3115（元）。因为总经理和副总经理工资特别高，就会使得这个公司所有成员工资的平均水平也表现得较高。但事实上，除去总经理和副总经理之外，剩余所有人的平均工资并不是很高，所以不能用月平均工资表示该公司员工收入的“平均水平”。

【点评】此题从统计表中收集数据，然后对所得数据进行整理，得到各类工资相对应的人数，即求得各类工资对应的权，从而利用加权平均数的求法解答问题。解答此类问题的关键是正确地从一个统计表中收集数据，正确理解每一类数据的“权”，从而利用加权平均数的求法成功解题。

典型应用二：从统计图中收集数据，求加权平均数

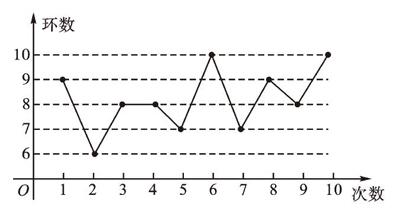
例2 某射击运动员在训练中射击了10次，成绩如图所示：

求这位射击运动员的射击成绩的平均数。

【解析】由图可得，10次成绩排序后为：6，7，7，8，8，8，9，9，10，10，也就是数据6出现1次，数据7出现2次，数据8出现3次，数据9出现2次，数据10出现2次，因此出现的次数1，2，3，2，2分别是成绩（环）6，7，8，9，10的权，则这位射击运动员的射击成绩的平均数=[110]（6×1+7×2+8×3+9×2+10×2）=8.2 （环）。

【点评】此题从折线统计图中收集数据，然后对所得数据进行整理，求得每类成绩出现的次数，即求得各类成绩的权，从而利用加权平均数的求法解答问题。解答此类问题的关键是正确地从一个统计图中收集数据，正确理解每一类数据的“权”，从而利用加权平均数的求法成功解题。

（作者单位：浙江省绍兴市柯桥区钱清镇中学）