区间直觉语言型Z-Numbers及其在多属性决策中的应用

陈万付， 梅孔椿

(1.安徽广播电视大学 滁州分校，安徽 滁州 239000;2.安徽大学 数学科学学院,安徽 合肥 230601)

为处理决策中的模糊性和不确定性,1965年Zadeh[1]提出模糊集(FS)理论,模糊集在过去的几十年间已被广泛应用于统计决策[2],模糊推理[3],模式识别[4]等领域,为了解决非隶属度的不确定性,Atanassov[5]提出了直觉模糊集(IFSs),但是随着社会的发展,问题的复杂化等影响,决策过程中的不确定性越来越明显,对此,Torra和Narukawa[6]提出了犹豫模糊集的概念(HFSs),其允许某一对象隶属于模糊集的程度以多个可能值的集合形式给出,而不像其他模糊集要求专家对属性值给定一个误差范围。然而,在现实决策问题中,经典模糊集的一些决策信息可能没有得到充分的考虑比如决策者的个人主观因素及属性客观因素等不确定因素,故2011年Zadeh[7]提出Z-number的概念,。为了让决策过程中的语言文字转化为数值集合Zadeh[8]在1975年提出了语言型变量的概念,Bao提出了语言型集合的语言评估尺度,将语言型集合转化为具体的数值,Wang和Peng提出了语言型尺度函数用来度量语言型集合。

本文在IILZNs为信息的多属性决策环境中,首先介绍了语言型集合,区间直觉语言型Z-numbers,然后提出和介绍了IILZNs型Z-numbers的定义以及运算法则,并通过一个例子介绍了如何将语言型集合通过尺度函数转化为具体的数值,其次基于尺度函数给出了IILZNs的距离公式时,给出了IILZNs的多属性决策方法。

1 知识准备

1.1 语言型集合

假设S={si|i=0,1,2,…,2m}是一个包含奇数个数的离散有序语言型术语的集合,其中m是一个正整数,si(i=0,1,2,…,m)代表语言型变量的一个可能值。比如当m=4,S可表示为S={s0=极度贫穷,s1=非常贫穷,s2=贫穷,s3=稍微贫穷,s4=一般,s5=稍微好,s6=好,s7=非常好,s8=极其好},且对于两个语言型变量si和sj满足以下两个性质[12]:

(1) 当si≤sj,当且仅当i≤j;

(2) 集合之间遵守互补运算:neg(si)=sj,当i+j=2m时。

1.2 区间直觉语言型Z-numbers

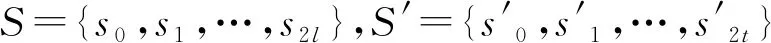
Z={(x,A(x),B(x))|x∈X}

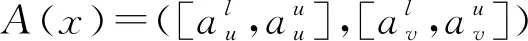
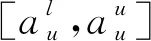
2 区间直觉语言型Z-numbers距离公式

(4)

(1)d(z1,z2)≥0

(2)d(z1,z2)=d(z2,z1)

(3) 当z1≤z2≤z3时,则有d(z1,z2)≤d(z1,z3)和d(z2,z3)≤d(z1,z3)

3 区间直觉语言型Z-numbers多属性决策方法

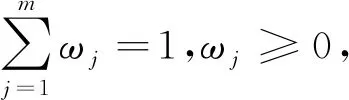
(5)

显然越小说明方案xi与理想解Z+的距离越小,则说明该方案越优。

为此,当属性权重完全未知时,可建立最优线性规划化模型如下:

用拉格朗日函数法可解得

(6)

下面给出具体决策步骤:

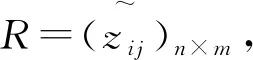
步骤2:构造最优线性规划模型并用式(6)计算各属性的权重。

步骤3:利用式(5)计算各方案到理想解的距离。

步骤4:根据各方案到理想解距离值大小进行排序,选择最优方案。

4 实例分析

供应链企业对3家合作企业即方案xi(i=1,2,3)优选,经过分析,交货期主要与服务水平、质量与技术水平、供应能力、价格四个属性有关,利用类似的案例分析,决策者对方案xi(i=1,2,3)关于属性Ci(i=1,2,3,4)给出评价,且所有评价都以犹豫直觉语言型Z-numbers的形式给出,决策矩阵如表1所示:

表1 语言型决策矩阵

步骤1:因为四个属性均为效益型属性,所以无需规范化矩阵,即

步骤2:由最优线性规划模型求得属性权重为wj=(0.3,0.2,0.2,0.3)T

步骤3:利用公式计算方案D1,D2,D3到理想解的距离为0.47,0.446,0.376。

步骤4:按照距离的大小对方案进行排序:x3fx2fx1,因此最优方案为x3。

5 结束语

本文在犹豫不确定语言型Z-numbers基础上提出了区间直觉语言型Z-numbers并对其多属性决策方法进行了研究,既考虑了隶属度与非隶属度,也考虑了决策过程中可能出现的不确定性,该方法首先提出了两种新的尺度函数用来度量语言型集合,将语言型集合转化为具体的数值以便用来比较语言型模糊集之间的优劣性,其次基于尺度函数提出了IILZNs的标准Hamming距离公式,最后对属性权重未知的IILZNs的多属性决策问题进行了研究,根据方案与理想解距离大小进行排序。该方法易于理解,计算简单,可以直接应用到综合评价问题中。