线性规划在水资源优化配置中的应用

曹亚群

(安徽水利水电职业技术学院，安徽 合肥 231603)

随着社会的不断发展,水资源出现了短缺,供需矛盾日渐突出,这些问题严重制约着社会经济的可持续发展,为了充分利用有限的水资源,让水资源最大限度地发挥社会、经济和环境效益,合理的优化配置水资源、提高水资源利用率是非常必要的。

1 水资源优化配置的原则[1]

所谓水资源优化配置是指在某个地区改善用水量和用水结构,对有限的水资源进行科学合理的分配和利用,其优化配置应遵循的原则如下:

(1)公平性原则。不同区域及社会各阶层之间进行水资源的合理分配。不同区域之间需做到协调发展,同一个区域内资源利用效益在社会不同阶层中公平分配。

(2)有效性原则。应以水资源的利用效益作为核算经济成本的重要指标,以生态环境的保护效益作为整个社会健康持续发展的重要指标。为了使水资源能充分被利用,应在水资源优化配置中树立环境目标、经济目标及社会发展目标,做到真正实际意义上的有效性。

(3)优先性原则。在各种用水中,优先分配的是生活用水,然后是生态环境用水,最后是生产用水。在保障人民生活、保护好生态环境的前提下加快经济发展。对于持续干旱时期,应该优先保障人民日常生活用水,同时考虑重点行业用水,然后是保障工业用水,最后是确保农业灌溉用水,在利用水资源时,应首先使用地表水,其次才是地下水。

(4)可持续性原则。它要求当代和后代、近期和远期在水资源的利用上有一个公平、协调发展,而非掠夺性的开采或破坏,也就是当代人利用水资源,不应该剥夺下一代人享有利用水资源的权利。

2 水资源优化配置属性[2]

水资源优化配置具有多水源、多要素、多用户及多目标的属性,同时具有一定的层次性与关联性,如图1所示。统筹考虑不同属性的重要程度,是水资源优化配置的前提。

图1 水资源优化配置属性关系

3 线性规划的模型

3.1 线性规划的一般形式

所谓线性规划,是指在一些约束条件下,求解某个具体目标最优(最小或最大)值的数学方法。其一般形式表示为[3]:

max(或min)Z=c1x1+c2x2+…+cnxn

s.t.{a11x1+a12x2+…a1nxn≤(=≥)b1

a21x1+a22x2+…a2nxn≤(=≥)b2

…,

an1x1+an2x2+…annxn≤(=≥)bn

x1,x2,…,xn≥0

3.2 线性规划的标准形式

鉴于在内容及形式上目标函数及约束条件的不同,线性规划问题有多种不同的表达式。因此,为了方便研究,制定了统一的算法,把线性规划的一般形式化成标准形式[4]:

max(或min)Z=c1x1+c2x2+…+cnxn

s.t.{a11x1+a12x2+…a1nxn=b1

a21x1+a22x2+…a2nxn=b2

…,

an1x1+an2x2+…annxn=bn

x1,x2,…,xn≥0;b1,b2,…bn≥0

把一般形化为标准形的过程,可以简而言之为“三化”:即目标最值化、约束等式化和变量非负化。

4 应用线性规划模型优化配置水资源[5]

某供水公司给生活、农业以及工业供水,年供水最大量6500×104m3,有关信息如表1所列。供水成本和水价不同导致获得利润也不同,在满足不同部门供水需求的前提下,为了获得最大供水利润,需要制定最佳配水方案。

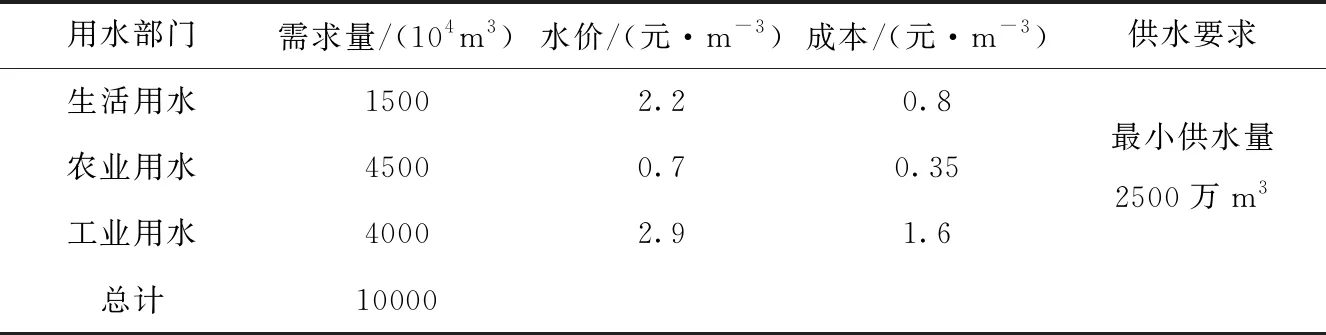
表1 供水信息

该供水公司向生活、农业、工业用水的供水量分别是X1×104m3、X2×104m3、X3×104m3目标函数为: MaxZ=(2.2-0.8)X1+(0.7-0.35)X2+(2.9-1.6)X3

约束条件是:{X1+X2+X3≤6500

0≤X1≤1500

2500≤X2≤4500

0≤X3≤4000

该模型可采用单纯形法来求解,得X1=1000×104m3,,X2=3000×104m3,X3=2500×104m3,供水最大利润为5700万元。也可以利用LIND0软件求解。

5 结束语

水资源优化配置目的是合理开发、高效利用水资源,促进经济、环境的可持续发展。目前水资源严重缺乏,我们必须重视水资源优化配置的研究,处理好社会、资源、经济及生态环境的关系,保证其可持续性发展。本文介绍了线性规划在水资源优化配置具体实例中的应用,明确目标函数及约束条件,然后用线性规划的求解方法求得最优解,在满足各方供水要求的同时,获得最大供水利润。事实上,在具体的生产实际中,目标函数和约束条件通常不是线性函数,这时还要用到非线性规划法、多目标规划法、动态规划法等,以达到更高要求的水资源的优化配置。