共享单车再平衡问题及其容差插入启发式算法

潘立军， 符 卓， 刘喜梅

(湖南工程学院 管理学院,湖南 湘潭 411104; 2.中南大学 交通运输工程学院,湖南 长沙 410075)

0 引言

共享单车系统作为共享经济的典型应用，在方便居民短距离出行、解决公交、地铁等公共交通“最后1公里问题”、缓解城市交通拥堵等方面发挥着重要作用。共享单车系统可分为有桩共享单车系统与无桩共享单车系统，有桩共享单车系统通过在规划的停放点设置固定单车停放锁具装置，用户可在停放点经授权取用单车。无桩共享单车系统则通过设置停放点电子地图围栏，同时加装单车电子锁具，配合专用手机APP来实现授权用户取用。近二年来，共享单车系统在我国快速普及，如永安行租车系统作为全国最大规模的有桩共享自行车系统已实现对100余个地级市的服务覆盖，而无桩共享自行车系统的代表——摩拜单车已在全国200多个城市投放共享单车。

无论是有桩还是无桩共享单车系统，停放点的单车容量均是有限的，通常共享单车系统初期会按周边用户分布情况规划该容量，但由于用户使用单车具有随机性、单向性等特点，必然导致一段时间后各停放点单车数量不均，有的停放点车多，无空余停放设施，有的停放点无车，对后续用户使用造成不便。因此，需定期组织载货车辆回收单车，再次投放到单车数不足的停放点，实现对各停放点单车数量的再平衡。随着共享单车在我国城市的快速普及，单车再平衡工作量与日俱增，如何科学组织城市内共享单车系统再平衡，已成为各大共享单车运营企业降本增效、提升服务质量的关键。

共享单车再平衡问题(Bike Sharing Rebalancing Problem, BRP)最早由Dell’Amico[1]提出，即利用有相同载重的车辆从自行车维护与补给中心出发完成一定区域内各单车停放点自行车的再分配，使各停放点达到预先设置的容量后回到中心，如何使所有的车辆行驶的距离或花费的时间、成本最少。BRP被认为是单一商品取送货车辆路径问题(One-commodity Pickup-and-delivery Capacitated Vehicle Routing Problem, 1-PDVRP)[2]的一个特例，即车辆出发时载重可不为零，但实践中，单车既可以回收到中心，也可从中心取车投放到各停放点，因此BRP与PDVRP有本质不同。针对BRP的求解，目前主要有二类算法，一是以分枝定界法为代表的精确算法[1,3～5]；二是启发式算法，如线路破坏与修复启发式算法[6]，该算法先假设车辆出发时载重为0，生成部分超出额定载重线路，最后调整车辆载重修复线路，使线路可行；线路再组合启发式算法[7]，局部迭代搜索启发式算法[8～10]等。从已有的研究报道分析来看，一是精确算法只适应小规模问题的求解，一旦问题规模扩大，精确算法将无能为力，二是由于车辆出发时载重可不为零，原来适用求解1-PDVRP的启发规则不适用BRP，已有启发式算法求解速度慢。因此深入研究BRP问题属性，设计快速高效的启发式算法对设计高效BRP调度软件至关重要。

1 BRP数学模型

从图论的角度，BRP可表示为一个完备图G=(V,E)，V={V1,V2,…,Vn}表示顶点集，其中V1表示自行车维护与补给中心，V′={V2,…,Vn}表示单车停放点集，E={(i,j)|i,j∈V,i≠j}表示弧集或边集。其符号定义为：M表示实施再平衡运输的专用车辆数；Q表示专用运输车辆的最大载重量，di表示车辆在第i个单车停放点取送量，di的可能的取值范围为[-Q,Q]，di小于零，表示该停放点需补充单车，di大于零，表示该停放点要回收单车；cij表示专用车辆访问弧(i,j)产生的运输成本或时间；θj表示专用车辆访问第j个停放点后的载重量，即车辆当前载重量。定义0-1决策变量xij，1表示车辆访问了弧(i,j)，否则为0。BRP的数学模型如下:

(1)

(9)

(1)式为目标函数，最小化运输总成本或时间，(2)式、(3)式确保除维护补给中心外其余单车停放点均被访问且只访问一次，(4)式、(5)式确保所有专用运输车辆在完成任务后均回到维护与补给中心，(6)式为消除子回路约束，(7)式、(8)式、(9)式为BRP车辆载重约束，确保各专用运输车辆在实施单车回收与投放过程中，车辆当前载重量不超过额定载重量。模型假设在某一停靠点回收的单车可被投放到任意其它需要的点，且车辆出发或者回到补给中心时，载重可不为零，因为可以事先装入部分单车，或者带回部分单车。BRP问题的新特点增加了问题求解难度，必须深入研究BRP模型性质，才能设计高效的启发规则。

2 BRP模型性质

设Route(V1,V2,…,Vi-1,Vi,Vi+1,…Vn)为一条可行线路，V1为自行车维护补给中心，Vi(i=2,3,…,n)为自行车停靠点，模型有以下性质:

性质1若Route可行，则必有max{θj}≤Q,min{θj}≥0(j=1,2,…,n)成立，反之也成立。

证明依据BRP的定义，性质1显成立。

性质2若Route可行，则在线路上任取两点Vi,Vj(i,j=1,2,…,n,且i≤j)，截取Vi至Vj两点之间的线路构成子线路Routec(Vi,Vi+1,…,Vj-1,Vj)仍为一条可行线路。

证明可依据反证法证明。

性质3若Route可行，则在线路上任取两点Vi,Vj(i,j=1,2,…,n,且i≤j)，对点Vi,Vj的取送量di,dj实施以下变换得到的新线路Route′仍可行。

变换(1)：

变换(2):

对于变换，因为:θ′i～j=(θi-min{θi,θi+1,…,θj-1,θj},…,θj-min{θi,θi+1,…,θj-1,θj}),而max(θ′i～j)≤Q,min{θ′i～j}=0,对于变换(2)，因为:θ′i～j=(θi+Q-max{θi,θi+1,…,θj-1,θj},…,θj+Q-max{θi,θi+1,…,θj-1,θj}),而min(θ′i～j)≥0,max{θ′i～j}=Q,故性质3成立。

定理1设Route为一条可行线路，Position(P1,P2,…,Pi-1,Pi,Pi+1,…Pn)为插入构造线路时可插入待访问取送点的位置(如图1所示)，设Pi位置可插单车数量范围为[Di,Ui]，若要保持插入后Route仍可行，则有:

Ui=Q+min{θ1,θ2,…,θi}-max{θi,θi+1, …,θn}

Di=-Q-min{θi,θi+1,…,θn}+max{θ1,θ2,…,θi}

图1 线路可插入位置示意图

充分性：

设dnew=Ui，依据性质3对Route的点V1,Vi,实施变换(1)后，线路仍可行；

再插入dnew点，则:

θ2-min{θ1,θ2,…,θi},…,

θi-min{θ1,θ2,…,θi},

θi+Q-max{θi,θi+1,…,θn},

θi+1+Q-max{θi,θi+1,…,θn},…,

θn+Q-max{θi,θi+1,…,θn})

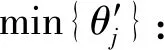
因为max{θ1,θ2,…,θi}≤Q(性质2，原线路的子路线可行)，故有：

又设dnew=Di，依据性质3对Route的点V1,V2,…,Vi-1,Vi,实施变换(2)后，线路仍可行；

再插入dnew点，则:

θ2+Q-max{θ1,θ2,…,θi},…,

θi+Q-max{θ1,θ2,…,θi},

θi-min{θi,θi+1,…,θn}),

θi+1-min{θi,θi+1,…,θn},…,

θn-min{θi,θi+1,…,θn})

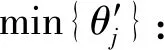
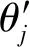
证明必要性：

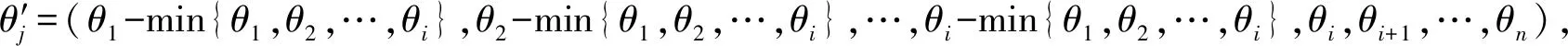
继续对Route′取(Vnew,Vi+1,…Vn)实施变换2，则变换后：θj″=(θ1-min{θ1,θ2,…,θi},θ2-min{θ1,θ2,…,θi},…,θi-min{θ1,θ2,…,θi},θi+Q-max{θi,θi+1,…,θn},θi+1+Q-max{θi,θi+1,…,θn},…,θn+Q-max{θi,θi+1,…,θn})，则:

dnew=(θi+Q-max{θi,θi+1,…,θn})-

(θi-min{θ1,θ2,…,θi})

=Q-max{θi,θi+1, …,θn}+

min{θ1,θ2,…,θi}=Ui

同理可证dnew=Di

必要性得证。

定理1阐明了BRP插入构造可行线路的量化判定条件，利用该条件可设计求解BRP的高效启发规则。

3 求解BRP的容差插入启发式算法

求解BRP的容差插入启法式算法的具体步骤如下：

第1步初始化待插入位置集合P，初始化待插入点集V，初始化待插入位置集合P，初始化解X={ }，初始化参数a1,a2；

第2步选取种子点，插入R1，更新X、V、P；

第3步找最优插入位置P*与最优待插入点V*。具体步骤如下：

WhilePi属于P

取位置Pi的前点Vi-1与后点Vi+1；

WhileVj属于V

计算位置Pi可插入单车数量的上界UPi，可插入单车数量的下界DPi(定理1)；

IfdVj∈[UPi,DPi]

计算容差(Capacity Range Length, CRL)；

CRLPi,Vj=UPi-DPi-|dVj|

(10)

计算线路增加；

SVj,Vi-1,Vi+1=cVj,Vi-1+cVj,Vi+1-cVi-1,Vi+1

(11)

Endif

Endif

Endif

CRL、S进行规一化处理，方法如式(12)、式(13)所示；

CRL′Pi,Vj=(CRLmax-CRL′Pi,Vj)/CRLmax

(12)

S′Vj,Vi-1,Vi+1=(Smax-S′Vj,Vi-1,Vi+1)/Smax

(13)

找到优插入位置P*与最优待插入点V*；

(14)

第4步插入点到当前解中，具体如下:IfV*,P*≠Ø。

将当前最优待插入点V*插入到最优位置P*，更新X、V；

Else

在V中重新选择种子点生成一条新的线路Rk，更新X、V集；

Endif

返回第三步；

算法终止条件：待插入点集V为空。

该算法为经典启发式搜索算法，启发规则主要考虑两方面因素：一是待插入点插入后的增加量，其越小越好；二是容差，类似于文献[12]中时差概念，容差反映了将待插入点插入到相应位置后，在保持线路可行的情况下，还可插入单车数量的大小，该数量越大，越有利于插入更多的点。为了能综合考虑两个因素，算法中采用归一化的方法将两类因素量纲统一，同时引入两个权重参数a1,a2(a1+a2=1) 将两个因素综合起来考虑，如式(14)所示。由于经典启发式搜索算法种子点的选取对算法的求解质量影响较大，本文采用文献[11]的方法，每次选待插入点中离补给中心距离最远的点作为当前种子点，这有助于提高求解质量。

4 算法测试

4.1 测试环境与测试方法

为了测试算法的求解效率，本文运用文献[2]收集的BRP问题集作为标准测试算例，该算例均来自全球各地共享自行车系统的实际应用数据，可在网站http://www.or.unimore.it-/resources/BRP/home.html下载。车辆载重量Q是该类问题的重要约束条件，Q越大则约束越松，反之则越紧。为了研究容差插入启发式算法求解不同载重容量限制问题的效率差异，本文将问题分为大容量问题(Q=30)、中容量问题集(Q=20)及小容量问题(Q<20)三个子集。

运用matlab 2014编程实现算法，运行于CPU(core i3，3.1GHZ)、Rom(4G)的PC机上。参数a1,a2的取值区间为[0.1,0.9]，每次变对0.1，每个算例分别运行10次，取最好解与平均解。

4.2 测试结果

在已报道的BRP求解的经典启发式算法中，只有文献[6]的线路破坏与修复启发式算法(DR_BRP)，本文算法将主要与其比较。

表1 大容量问题测试结果(Q=30)

在求解质量上，文献6在构建初始解后运用了邻域搜索，求解质量较高，本文算法在3类不同测试问题集上，整体求解质量低于当前最优解，分别为9.1%(Q=30)、14.6%(Q=20)、13.9%(Q<20)，算法对大容量问题的求解质量优于中容量问题与小容量问题，中、小容量问题求解质量差距不明显。本文算法共找到11个问题的当前最优解，其中在问题Minneapolis(116/10)上找到了当前新的最好解，优于当前最好解1.7%(见表3)。

表2 中容量问题测试结果(Q=20)

从求解的速度来看，两算法均运行于CPU(core i3，3.1GHZ)、Rom(4G)的PC机上，本文算法在求解速度上显示出较大优势，求解三类问题的平均速度均为0.02秒，优于文献6的89.20秒(Q=30)、116.56秒(Q=20)、136.43秒(Q<20)。

在参数设置上，本文算法为2个，DR_BRP为5个，本文算法的最优参数设置a1为[0.1,0.4]，a2为[0.6,0.9]。表中平均解偏离计算方法为(平均解-最好解)/最好解，反映算法求解稳定性。

表3 小容量问题测试结果(Q<20)

5 结论及研究展望

BRP虽为1-PDVRP的特例，但由于车辆出发或回来时载重可不为零，故BRP线路有其独特的性质，本文深入研究了该问题的线路可行变换性质，证明了插入构造可行解的充要条件，在此基础上，引入容差概念，并提出了容差插入启发式算法，应用标准算例测试表明算法速度快，均可在1秒内求出较好解，参数设置简单；算法对11个问题可找到当前最优解，其中1个问题找到新的当前最好解；算法对大容量问题的求解质量优于中、小容量问题。

BRP是共享经济背景下一类资源投放的再平衡问题，除了共享单车，其它共享设施如雨伞、微型汽车等设施同样也有再平衡的需求，因此该类问题有较强的应用背景。同时由于物联网的使用，共享设施的再平衡问题规模变的越来越大，因此，依据问题特点设计良好的启发规则，进而设计针对大规模共享设施再平衡问题的高效智能启发式算法值的后续深入研究。