应用驱动的企业信息系统动态数据更新策略研究

宗 威， 吴 锋， 刘 玮

(1.西安电子科技大学 经济与管理学院，陕西 西安 710126; 2.西安交通大学 管理学院，陕西 西安 710049； 3.过程控制与效率工程教育部重点实验室，陕西 西安 710049)

0 引言

在物联网与移动智能终端飞速发展的今天，数据来源众多，变化速度较快，多源、实时、多变的大数据环境为企业有效管理信息系统中的动态数据带来巨大挑战[1,2]。据统计，在2014年，企业信息系统中过时数据产生的成本高达1.7万亿美元[3]。企业若要实现数据的价值，必须保证信息系统能够快速响应大数据的变化[4]。以ERP系统为例，倘若ERP系统数据没有根据外界数据源的变化及时更新，那么基于过时数据所做出的决策必定是错误、无效的，势必会给企业带来经济损失，影响企业的竞争力；相反，如果无计划地更新ERP系统，将直接扰乱系统中各类计划的正常稳定运行，使得按计划运作的ERP系统无所适从，还会因此而产生数据更新成本，影响ERP系统的运行效果。因此，如何结合企业对数据及时性的具体应用需求，制定最佳的ERP系统动态数据更新策略，解决数据更新策略之间的冲突，实现数据过时成本与更新成本的最佳权衡成为运营管理与信息管理领域的热点及难点问题。

在信息系统中，决定数据的最优更新策略以反映数据源数据变化的过程称之为数据同步、视图维护或数据库检查[5]。国内有关数据及时性的研究主要集中在计算机、数据库等领域。张鹏等[6]通过减少数据更新过程中的冗余计算，提高数据视图的更新效率。武彤等[7]研究了基于查询频率的视图更新算法，以缩短查询响应时间，提高查询效率。郑凯等[8]研究了大容量物理存储条件下数据仓库的最佳视图选择问题，提出了面向查询集覆盖的物化视图选择算法，以提高视图选择效率、缩短应答用户查询时间。通过对上述文献的总结分析发现，目前国内学者皆通过提高查询效率、缩短系统响应时间等方式提高数据的及时性，忽略了企业对数据及时性的具体应用需求，没有考虑数据更新成本与数据过时成本对企业决策的影响。

在国外研究方面，Segev and Fang[9]提出了基于时间与查询量的最优更新策略，其目标是使数据用户获取查询的时间最短，忽略了更新决策对数据的具体应用需求。Ling和Mi[10]以及Dey等[11]将数据到达过程刻画为泊松过程，通过权衡数据过时与更新成本，研究数据库更新的最优固定时间间隔。Fang等[12]也将数据到达过程刻画为泊松过程，提出了根据系统中各个决策点的查询状态制定数据库中知识(如关联规则)更新的最优策略。

通过总结分析上述国内外有关数据更新策略的文献，发现存在以下不足：1)国内有关数据及时性的研究以计算驱动为主，即通常关注数据更新算法的准确率与运行效率，忽略了数据的应用对企业决策的影响，不能很好地解决实际问题；2)国外有关数据及时性的研究虽然在一定程度上考虑了数据过时成本或数据更新成本对企业决策的影响，但这些数据更新策略大都基于固定的更新周期，灵活性较差，不能满足大数据环境下企业信息系统对数据及时性的要求。因此，本文以企业ERP系统动态的采购数据更新为研究对象，从企业对数据及时性的实际应用需求角度出发，提出一种应用驱动的、基于非固定周期的数据更新策略，通过与传统的固定周期更新策略相比较，验证本文所提出的数据更新策略的有效性。

1 问题描述

在ERP系统中，采购数据直接反映了物料或产品当前的库存水平，在制造企业制定采购决策过程中发挥重要作用。为了更清楚地描述研究问题，本文只考虑一种查询的情形，即库存查询。数据用户在制定采购决策前，首先需要将库存查询传送给ERP系统，以获取物料当前的库存状态。但随着新的采购数据不断到达，使得系统中先前存储的库存数据因过时而失效，因此必须及时更新ERP系统中的采购数据，才能准确反映库存数据的变化，为采购决策的制定提供坚实的数据基础。如果不及时更新ERP系统中的采购数据，那么库存查询获取的数据是过时的，由此会导致仓储部门无法正常出料、生产部门无法正常领料、销售部门无法正常安排销售等严重后果，无法保证生产计划的有序、稳定开展，最终给企业带来一定的经济损失。相反，如果不断用新到达的采购数据更新ERP系统，虽然能够保证数据的及时性，却在一定程度上扰乱了ERP系统中各项计划的稳定性，也由此而产生了系统更新成本。因此，当ERP系统接收到库存查询时，需要结合企业对数据的实际应用需求，考虑是否用新到达的采购数据更新ERP系统，从而使数据过时成本与更新成本之和最小。采购数据的更新过程如图1所示。

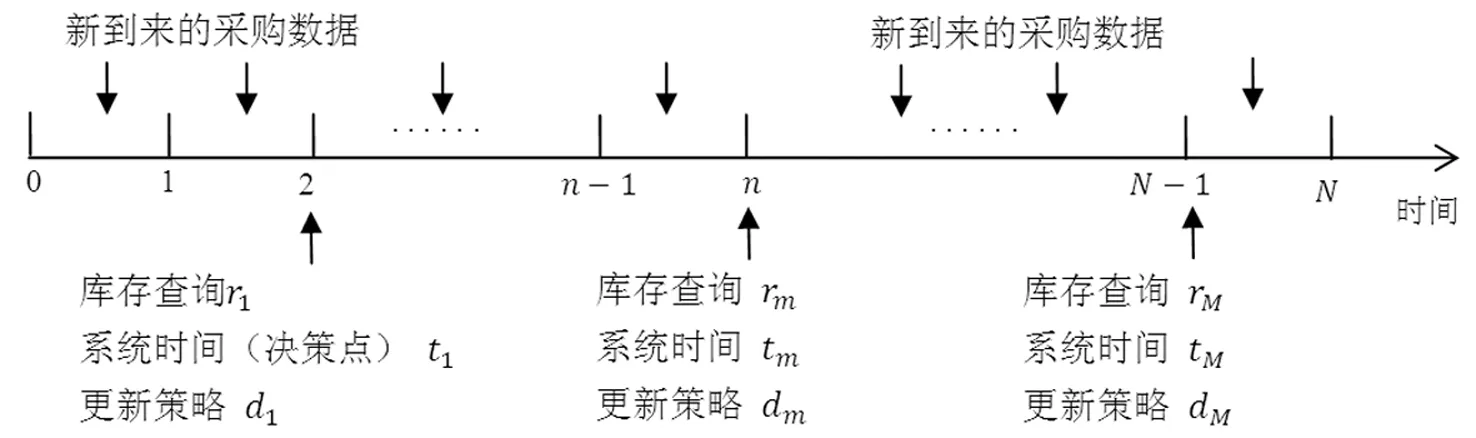
图1 ERP系统中采购数据更新过程

2 应用驱动的数据更新模型

本文将ERP系统中采购数据更新过程刻画为马尔科夫决策过程[12,13]。文中用到的符号及其含义如表1所示。

表1 符号及释义

2.1 系统状态与转移概率分析

有学者证明，查询与数据到达信息系统中的过程可以近似刻画为泊松过程[10,11,14]。因此，根据泊松过程的性质与特点，本文假设单位时间内到达ERP系统的采购数据的数量与库存查询的个数分别服从参数为λu与λr的泊松分布。假设在整个决策时间范围内，平均到达ERP系统的库存查询总量是M。系统时间tm指的是第m个库存查询到达ERP系统的时间，m=1,2,…,M。tm也可理解为决策点，因为当第m个库存查询到达ERP系统时，需要做出是否更新ERP系统的决策dm。更新决策dm只能取0或1。dm=0表示不更新ERP系统，dm=1表示更新ERP系统。dm的取值由系统状态sm决定。本文将系统状态sm定义为：到tm时刻为止累积的采购记录的数目。一条采购记录描述了某个物料的具体细节，如物料名称、采购日期、采购价格等等。同时，在tm时刻所做出的决策dm会影响到ERP系统在tm+1时刻的系统状态sm+1。由于dm的不同取值，系统状态sm+1的取值也应该分别讨论。

当dm=0时，表示不更新ERP系统。此时，在tm时刻累积的采购记录数量会随之累积到下一时刻tm+1。当dm=1时，表示更新ERP系统。此时，在tm时刻累积的采购记录数量被输入到ERP系统中，而不会累积到tm+1时刻。综上所述，tm+1时刻的系统状态sm+1如式(1)所示，Im,m+1表示系统在tm时刻与tm+1时刻的时间间隔内累积的采购记录数量。

(1)

系统从当前状态sm到下一时刻状态sm+1的转移由转移概率Psm,dm,sm+1控制。当第一个库存查询在t1时刻到达ERP系统时，需要根据当前的系统状态s1做出更新策略d1，然后ERP系统将以转移概率Ps1,d1,s2随机地转移到下一状态s2。当第二个库存查询到达ERP系统时，需要根据系统状态s2做出更新策略d2，然后ERP系统以转移概率Ps2,d2,s3随机地转移到下一状态s3。以此类推，系统状态转移过程如图2所示。

由于到达ERP系统的库存查询个数服从参数为λr的泊松分布，则两个连续到达的库存查询之间的时间间隔服从参数为λr的指数分布。因此tm时刻与tm+1时刻之间累积采购记录数量为h的概率P(Im,m+1=h)如式(2)所示。

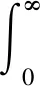
f(tm+1-tm)d(m+1-tm)

(2)

其中，f(tm+1-tm)是时间间隔(tm+1-tm)的概率密度函数，且f(tm+1-tm)=λre-λr·t。如果令(tm+1-tm)=t，则式(2)可以表示为:

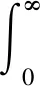
(3)

当dm=0时，由式(1)可以得出：

Im,m+1=sm+1-sm

(4)

此时，式(3)中的参数h应由式(4)表示，则有

Psm,dm=0,sm+1=P(Im,m+1=sm+1-sm)

(5)

当dm=1时，由式(1)可以得出：

Im,m+1=sm+1

(6)

此时，式(3)中的参数h应由式(6)表示，则有:

Psm,dm=1,sm=1=P(Im,m+1=sm+1)

(7)

2.2 系统成本分析

由于dm的不同取值，系统成本cm(sm,dm)也应该分别讨论。如果dm=0，意味着在tm时刻不更新ERP系统，此时第m个库存查询所获得的数据有可能是过时的，基于过时的库存数据所做出的采购决策会给企业带来一定的经济损失，可称之为过时成本，如式(8)中的cs(sm)所示。如果dm=1，意味着在tm时刻更新ERP系统，此时虽然避免了过时成本，但却产生系统更新成本，如式(8)中的cu所示。有学者已经证明，系统更新成本与到达的数据量无关，是常数[11]。综上所述，tm时刻的系统成本如式(8)所示。

(8)

过时成本cs(sm)反映了累积采购记录数量对采购决策的影响。如果不更新ERP系统，那么新到达的采购记录不会被输入到ERP系统中，此时库存查询获取的数据是无效的、不准确的，甚至会由此产生不必要的采购，从而产生采购成本cp与库存成本cI。本文将过时成本定义为如式(9)所示的形式：

cs(sm)=(cp+cI)·F(sm)

(9)

其中采购成本cp与库存成本cI均为常数，F(sm)是数据过时函数，表示系统状态sm过时的概率分布，即系统状态sm的累积分布函数[12]。由式(9)可以看出，过时成本的大小取决于在tm时刻累积的采购记录数量的多少。ERP系统在tm时刻累积的采购记录数量越多，数据过时的可能性就越大，企业制定错误采购决策的可能性也就越大，那么由此产生的过时成本就越高。因此，cs(sm)是系统状态sm的增函数。此外，当sm=0时，令F(sm)=0，那么cs(sm)=0，这表示如果在tm时刻累积的采购记录数量为0，意味着ERP系统中的采购数据是最新的，此时就不会产生过时成本。基于在tm时刻所做的更新决策以及相应的成本(即式(8))，ERP系统中采购数据更新问题的目标函数可以表示为：

(10)

为了分析方便，式(10)可以写为如下形式：

C=minE(c1(s1,d1)+c2(s2,d2)+…+cM(sM,dM))

(11)

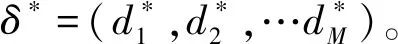
3 算法分析与设计

3.1 最优更新策略分析

基于式(11)与马尔科夫决策理论，令V1=E(c1(s1,d1)+c2(s2,d2)+…+cM(sM,dM))，表示从t1时刻到tM时刻的期望总系统成本(也即值函数)。同理，令V2=E(c2(s2,d2)+…+cM(sM,dM))，表示从t2时刻到tM时刻的期望总系统成本。由此可得V1=c1(s1,d1)+V2，Vm=cm(sm,dm)+Vm+1。ERP系统在tm时刻的期望总系统成本Vm可以被认为是系统在tm时刻的系统成本cm(sm,dm)与系统在tm+1时刻期望总系统成本Vm+1之和。当m=M时，令VM+1=0，因此VM=cM(sM,dM)。由于到达ERP系统的采购记录数量是随机的，所以应该考虑ERP系统从当前状态转移到下一状态的所有可能情况。综上所述，ERP系统在tm时刻的期望总系统成本Vm表示为:

Vm=cm(sm,dm)+∑sm+1∈SPsm,dm,sm+1·Vm+1

(12)

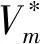
(13)

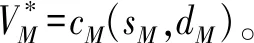
基于式(13)，我们定义如下关系式(14)

(14)

马尔科夫决策过程的一个重要特性就是最优策略的单调性。然而，这一特性只有在目标函数最大化的情形下成立。由于本文的目标函数是最小化期望总系统成本，因此需要将本文的最小化目标函数(式(13))转化成最大化目标函数的情形，如式(15)所示。

定义1若函数g(x,y)在X×Y上是超加的，则对于x+≥x-,y+≥y-，有：

g(x+,y+)+g(x-,y-)≥g(x+,y-)+g(x-,y+)

(16)

基于式(15)，给出马尔科夫决策过程中最优策略单调性的定理：

定理1对于式(15)而言，令m=1,2,…,M-1，如果：

(1)对于所有的dm∈D，-cm(sm,dm)是sm的非增函数；

(2)对于所有的sm+1∈S与dm∈D，∑sm+1∈SPsm,dm,sm+1是sm的非减函数；

(3)-cm(sm,dm)在S×D上是超加函数；

(5)对于所有的dM∈D-cM，(sM,dM)是sm的非增函数；

证明a)当dm=0时，基于式(8)可以得出-cm(sm,dm=0)=-cs(sm)。由式(9)可知，cs(sm)是系统状态sm的增函数，因此-cs(sm,dm)是sm的非增函数。当dm=1时，有-cm(sm,dm=1)=-cu，其中cu是常数。综上所述，对于所有的dm∈D，-cm(sm,dm)是非增函数，定理1中的条件(1)成立。

b)在证明定理1中的条件(2)时，首先令sm=am，sm+1=an。

当dm=0时，由式(5)可知：

∑sm+1∈SPsm,dm=0,sm+1

(17)

当dm=1时，由式(7)可知：

∑sm+1∈SPsm,dm=0,sm+1

(18)

式(18)中没有参数sm，因此式(18)是个常数。

综上所述，∑sm+1∈SPsm,dm,sm+1是sm的非减函数，定理1中的条件(2)成立。

c)令s+≥s-。首先考虑d+>d-的情形。d+>d-意味着d+=1，d-=0，根据定义1以及式(8)，可以得出:[-cm(s+,d+)]+[-cm(s-,d-)]=-cu+[-cs(s-)]以及[-cm(s+,d-)]+[-cm(s-,d+)]=-cs(s+)+(-cu)由于cs(sm)是系统状态sm的增函数，那么当s+≥s-时，cs(s+)≥cs(s-)，所以[-cm(s+,d+)]+[-cm(s-,d-)]≥[-cm(s+,d-)]+[-cm(s-,d+)]，即当s+≥s-d+>d-时，-cm(sm,dm)是超加函数。

当d+=d-=0时，由定义1和式(8)可知：[-cm(s+,d+)]+[-cm(s-,d-)]=[-cs(s+)]+[-cs(s-)]以及[-cm(s+,d-)]+[-cm(s-,d+)]=[-cs(s+)]+[-cs(s-)]由于[-cm(s+,d+)]+[-cm(s-,d-)]=[-cm(s+,d-)]+[-cm(s-,d+)]，因此当s+≥s-以及d+=d-=0时，-cm(sm,dm)是超加函数。

最后，当d+=d-=1时，由定义1和式(8)可知：[-cm(s+,d+)]+[-cm(s-,d-)]=(-cu)+(-cu)以及[-cm(s+,d-)]+[-cm(s-,d+)]=(-cu)+(-cu)由于[-cm(s+,d+)]+[-cm(s-,d-)]=[-cm(s+,d-)]+[-cm(s-,d+)]，因此当s+≥s-以及d+=d-=1时，-cm(sm,dm)也是超加函数。

综上所述，-cm(sm,dm)在S×D上是超加函数。

d)令s+≥s-。由定义1可知，若要证明∑sm+1∈SPsm,dm,sm+1·Gm+1是超加函数，必须证明下式成立

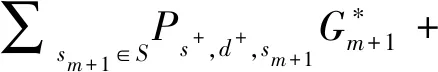
首先考虑d+>d-的情形，即d+=1且d-=0，由定义1及式(17)与(18)可知:

∑sm+1∈SPs+,d+=1,sm+1+∑sm+1∈SPs-,d-=0,sm+1

以及

∑sm+1∈SPs+,d-=0,sm+1+∑sm+1∈SPs-,d+=1,sm+1

前面已经证明∑sm+1∈SPsm,dm,sm+1是sm的非减函数，因此当s+≥s-时有:

∑sm+1∈SPs+,d+=1,sm+1+∑sm+1∈SPs-,d-=0,sm+1

≤∑sm+1∈SPs+,d-=0,sm+1+∑sm+1∈SPs-,d+=1,sm+1

(19)

式(19)可以写成如下形式：

-∑sm+1∈S(Ps+,d+=1,sm+1+Ps-,d-=0,sm+1)≥

-∑sm+1∈S(Ps+,d-=0,sm+1+Ps-,d+=1,sm+1)

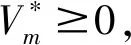
(20)

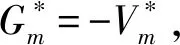
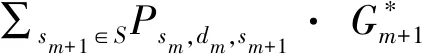
其次考虑d+=d-时情形，即d+=d-=0或d+=d-=1时，有

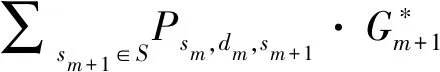
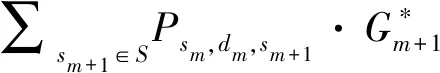
e)由式(7)可知，当m=M且dM=0时，有-cM(sM,dM=0)=-cs(sM)。根据前文的分析，已知cs(sm)是系统状态sm的增函数，因此当dM=0时，-cs(sM,dM)是非增的。当dM=1时，-cM(sM,dM=1)=-cu，其中cu是常数。综上所述，对于dm∈D，-cM(sM,dM)是非增函数。

(21)

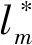
3.2 算法设计

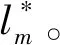
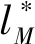
R(sM,dM=0)≥R(sM,dM=1)

(22)

cs(sM)≥cu

(23)

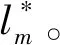
图3 ERP系统中采购数据最优更新策略求解算法

4 算例

为了验证本文提出的ERP系统采购数据最优更新策略的有效性，采用来自于红门智能科技股份有限公司(以下简称“红门公司”)的真实数据作为实验对象。红门公司(http://www.hongmen.com/)位于广东省深圳市，是目前全国最大的电动门、电动伸缩门生产与研发基地之一。红门公司主要生产和研发电动伸缩门、智能停车场管理系统等产品，于2011年5月上线并实施SAP-R/3系列的ERP平台与系统。由于该公司生产的产品种类众多，需要采购与管理的物料种类及数量繁多，为保证ERP系统采购数据的及时性带来了巨大挑战，这也是本文选择红门公司的实际数据作为实验对象的主要原因之一。

4.1 参数设置

首先，本文中的单位时间指的是一天，整个决策时间范围设置为365天，即一年。通过调研红门公司的实际情况发现，每天到达ERP系统的平均采购记录数量为182条，因此设置采购数据的平均到达率λu为182。红门公司平均每七天查询一次物料库存状态，因此库存查询的平均到达率λr为1/7。通过与红门公司的ERP系统运维管理人员访谈得知，更新成本cu主要由计算成本与人力成本构成。计算成本指的是更新ERP系统的软硬件成本，人力成本指的是更新ERP系统时所付出的人力成本。根据红门公司实施ERP系统的软硬件投入情况可知，ERP系统的单位平均更新成本为1300RMB，单位平均人力成本为230RMB。因此，更新成本cu为1530RMB(1300RMB+230RMB)。对于过时成本cs(sm)=(cp+cI)·F(sm)而言，由前面的分析可知，cp与cI分别代表平均采购成本与库存成本，F(sm)是系统状态sm的累积分布函数。通过对红门公司的调研及计算得出，平均采购成本为1000RMB，库存成本为2500RMB。那么，过时成本可以表示为cs(sm)=3500·F(sm)。

4.2 有效性分析

通过与传统的基于固定周期的数据更新策略相比较，验证本文提出的采购数据最优更新策略的有效性。基于固定周期的数据更新策略主要分为以下三类[11]：

(1)固定时间间隔的数据更新策略。也被称作周期性数据更新策略，即信息系统每经过一段固定的时间间隔后更新。例如每五个小时更新一次。

(2)固定查询数量的数据更新策略。在这种数据更新策略下，当系统接收到固定量的查询后更新。例如信息系统每接收到五个查询后更新一次。

(3)固定新数据量的数据更新策略。在这种数据更新策略下，当系统接收到固定量的新数据后更新。例如，当到达信息系统的新数据量累积或超过五条记录时，更新系统。

令C表示实施本文提出的数据更新策略时的最优期望总系统成本，Ctime表示实施固定时间间隔的数据更新策略时的期望总系统成本，Crequest表示实施固定查询数量的数据更新策略时的期望总系统成本，Cupdate表示实施固定新数据量的数据更新策略时的期望总系统成本。在第一个实验中，我们先考虑F(sm)为指数分布的累积分布函数的情形(用Fexponential表示)，如式(24)所示，

F(sm)=Fexponential(sm)=1-e-λ·sm)

(24)

其中λ是参数。为了验证本文提出的数据更新策略的鲁棒性与有效性，在实验过程中考虑了参数λ不断变化的情况。上述四种数据更新策略的实验结果如表2所示。从表2中可以明显地看出，所有四种数据更新策略的最优期望总系统成本随着参数"λ" 的增加而增加，但本文提出的数据更新策略的最优期望总系统成本均比其他三个基于固定周期的数据更新策略的最优期望总成本要小。也就是说，本文提出的基于非固定周期的采购数据更新策略是有效的。

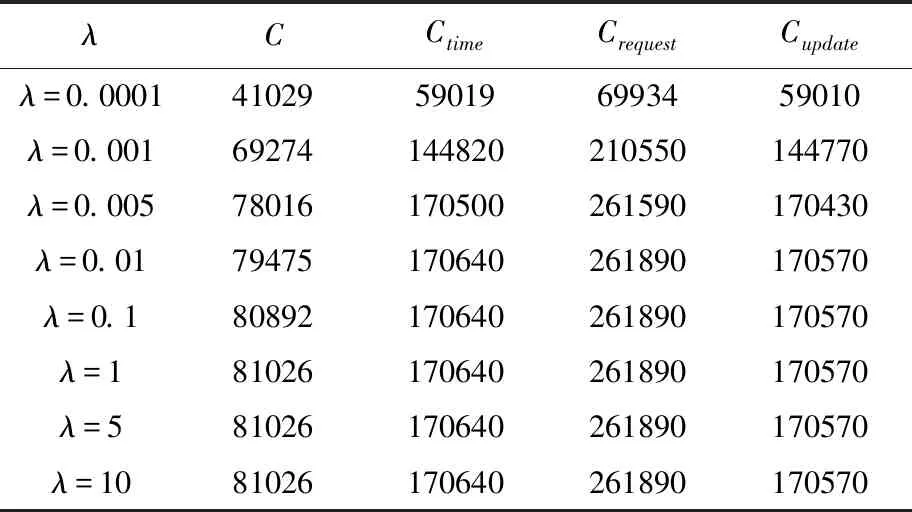
表2 实施不同数据更新策略时的最优期望总系统成本

此外，本文还考虑了F(sm)函数的不同形式对最优期望总系统成本的影响。除了指数分布的累积分布函数以外，又选择了其他两种不同形式的单调递增概率函数。Logistic函数(用Flogistic表示)是单调递增的S型函数形式，如式(25)所示。均匀分布的累积分布函数(用Funiform表示)是单调递增的分段线性函数，如式(26)所示。由于F(sm)函数表示的是sm的概率分布，因此上述两种函数的值域范围是[0,1]。

(25)

(26)

由前文分析可知，当sm=0时，应该有F(sm)=0。理论上讲，当式(25)中参数α的取值无限大时，才能满足sm=0时，F(sm)=0的要求。经测算，当参数α的取值为7时，有F(sm=0,α=7)=0.00091105。因此，式(25)中参数α的取值应大于或等于7。此外，当固定参数β与sm时，Flogistic(sm)的值随参数α的增加而减小，当α=7时，Flogistic(sm)取得最大值，能够反映最差情形下本文所提出的应用驱动数据更新算法的表现情况。因此，本文令α=7。四种数据更新策略在不同F(sm)函数下的最优期望总成本对比结果如表3所示。

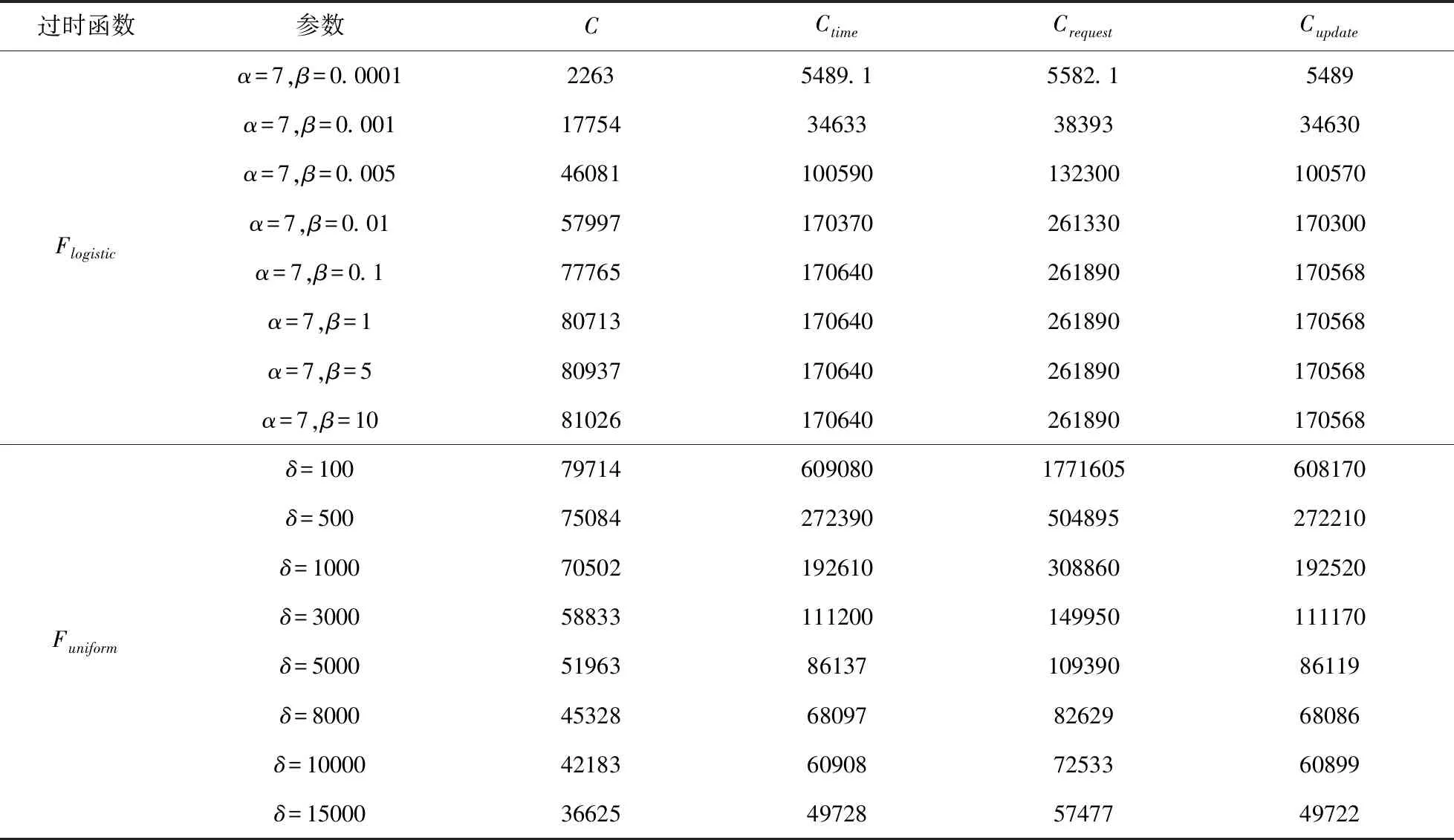
表3 数据更新策略在不同形式过时函数下的最优期望总成本对比结果

表3的实验结果表明，尽管过时函数与参数不断变化，本文提出的应用驱动的、基于非固定更新周期的采购数据更新策略明显优于其他三个传统的、基于固定周期的数据更新策略。当过时函数为Logistic函数时，所有四种数据更新策略的最优期望总成本随参数β的增加而增加。这是因为当参数α和sm固定时，式(25)中Flogistic(sm)函数值随参数β的增加而增加，因此最优期望总系统成本呈现增长趋势。当过时函数为均匀分布的累积分布函数时，所有四种数据更新策略的最优期望总成本随参数δ的增加而减小。这是因为当系统状态sm固定时，式(26)中Funiform(sm)函数值随参数δ的增加而减小，因此最优期望总系统成本呈现下降趋势。此外，在表2与表3的对比结果中可以发现，对于三个基于固定周期的数据更新策略而言，基于固定新数据量的数据更新策略要优于基于固定时间间隔的数据更新策略与基于固定查询数量的数据更新策略，这与文献[11]的研究结论相一致。

5 结论

在大数据时代，数据及时性已经成为企业日益关注的数据质量关键问题之一。由于大数据的产生速度和变化速度较快，数据的“有效期”非常之短，使得企业ERP系统极易出现过时、失效的数据，这些无效数据不仅影响ERP系统的运作效果，还将直接影响企业决策的有效性与准确性。虽然国内外学者针对动态数据的及时性问题展开了研究，但主要存在以下问题：1)国内有关数据及时性的研究以计算驱动为主，忽略了企业对于数据的应用需求与数据的具体应用环境，不能很好地解决实际应用问题；2)国外有关数据及时性的研究虽然在一定程度上考虑了过时数据对企业决策的影响，但这些数据更新策略大都基于固定的更新周期，灵活性较差，不能满足大数据环境下的企业信息系统对数据及时性的要求。因此，本文在前人研究基础之上，以企业ERP系统中动态的采购数据更新为研究对象，将动态数据更新过程刻画为马尔科夫决策过程，进一步结合企业对数据及时性的实际应用需求，提出一种应用驱动的、基于非固定周期的动态数据更新策略，并通过一系列数值分析将其与当前常用的、基于固定周期的数据更新方法进行比较。研究发现，无论当过时函数为指数分布函数、Logistic函数或是均匀分布函数时，应用驱动的、基于非固定周期的动态数据更新模型始终优于传统的基于固定周期的数据更新模型，这是因为应用驱动的动态数据更新方法不仅关注数据本身，还更加关注数据对最终决策的影响以及企业对于数据的实际应用环境和应用需求，同时，该方法还具有较好的稳健性。然而，本文的模型只考了一种查询类型的情形，对于信息系统中动态数据同时影响多类查询的情形，是一个值得研究和探索的方向。