一元一次方程应用题解法归类

文 许贤洁

第四章 一元一次方程

领 衔 人：张伟俊

组稿团队：江苏省常州市武进区张伟俊名师工作室

一、数字问题

例1有一个两位数，两个数位上的数字和是10，如果把个位与十位上的数字对调，那么所得的两位数比原来的两位数大54，求原来的两位数。

【分析】设原来的两位数个位上的数字为x，则根据题意，有：

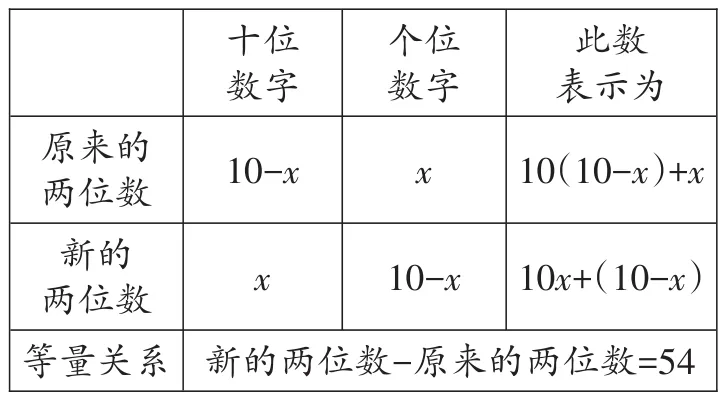
原来的两位数新的两位数等量关系十位数字10-x个位数字x此数表示为10（10-x）+x x 10-x 10x+（10-x）新的两位数-原来的两位数=54

对于数字问题，最常见的就是已知一个多位数，然后每个数位上的数字进行位置变换后，得到一个新的数字。新的数字与原来的数字有数量关系，这是解决这类题目的关键。一般将一个数各数位上的数字设成未知数后，如果要表示这个数，十位上的数字要乘10，百位上的数字要乘100，以此类推。

二、分配问题

例2某制衣厂计划若干天完成一批服装的订货任务。每天生产20套服装，就比订货任务少100套；每天生产23套服装，就可超过订货任务20套。问这批服装的订货任务是多少套？

【分析】设计划x天完成这批服装，由题意，我们可以画出如下分析图：

所以可得23x-20=20x+100。

对于分配问题，要弄清楚两次分配方法下的生产数量与订货任务之间的关系，解决的关键是找到两次分配方法下的生产数量之间的关系，即等量关系。像这类问题，用画线段图的方法较为直观。

三、配套问题

例3某车间有22名工人生产螺钉和螺母，每人每天平均生产螺钉1200个或螺母2000个，一个螺钉要配两个螺母。为了使每天生产的产品刚好配套，应该分配多少名工人生产螺钉？多少名工人生产螺母？

【分析】设分配x名工人生产螺钉，则生产螺母的人数为（22-x）名，生产螺钉1200x个，生产螺母2000（22-x）个。等量关系：2×每天的螺钉数=每天的螺母数。

解决这类题目的基本等量关系就是：加工（或生产）的各种零配件的总数量比等于一套组合件各种零配件的数量比。若m件A产品与n件B产品配套，其等量关系是“A产品的件数×n=B产品的件数×m”。

四、行程问题

例4甲、乙两站相距480公里。一列慢车从甲站开出，每小时行驶90公里。一列快车从乙站开出，每小时行驶140公里。

（1）慢车先开出1小时，快车再开。两车相向而行。快车开出多少小时后两车相遇？（2）慢车开出1小时后两车同向而行，快车在慢车后面，快车开出后多少小时追上慢车？

【分析】基本数量关系：路程=速度×时间，时间=路程÷速度，速度=路程÷时间。等量关系：①相遇问题，快车行驶的路程+慢车行驶的路程=两车原距离；②追及问题，快车行驶的路程-慢车行驶的路程=两车原距离。解决此题的关键是要理解清楚相向、相背、同向等含义，弄清行驶过程。

五、工程问题

例5将一批资料录入电脑，甲单独做需18h完成，乙单独做需12h完成。现在先由甲单独做8h，剩下的部分由甲、乙合做完成，甲、乙两人合作了多少时间？

【分析】设甲、乙两人合作了xh，由题意，可得如下表格：

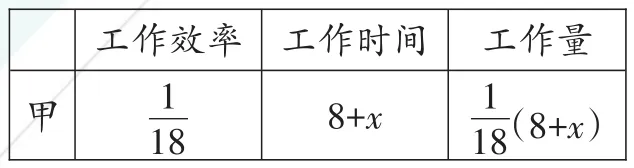
工作效率工作量甲1工作时间8+x 1 18 18（8+x）

等量关系：（1）甲的工作量+乙的工作量=全部的工作量。

工程问题是常考题型，而且工程问题也有多种考试题型。同学们只需要记住：工作效率×工作时间=工作总量。如果工作总量没有给出具体的数量，一般看作单位1。

六、打折销售问题

例6一家商店某种裤子按成本价提高50%后标价，又以八折优惠卖出，结果每条裤子获利10元，则每条裤子的成本是多少元？

【分析】打折销售问题中几种量的关系是：

公式：利润=进价×利润率；售价=标价×折扣数；利润=售价-进价；总利=单利×数量。

综上所述，列一元一次方程解应用题的实质就是先把实际问题转化为数学问题（设元、列方程），再通过解决数学问题的方式解决实际问题（解方程、写出答案）。在这个过程中，我们可以用到“图示法”“列表法”“公式法”等，而找到等量关系是关键。