基于松弛算法的散焦显微粒子图像追踪

王梓屹

摘要：为了开展三维显微粒子追踪测速研究，本文搭建了一套高速显微散焦粒子图像三维测速系统。针对散焦粒子图像获取方法及粒子空间坐标的标定，编写了邻近算法和松弛算法，结果表明粒子密度较大时，松弛算法明显优于邻近算法。

关键词：显微粒子;散焦成像;松弛算法

中图分类号：TP311 文献标识码：A

文章編号：1009-3044（2019）29-0198-03

近三十年来，微电子机械系统（MEMS）技术的出现和仪器设备的微型化要求，极大地促进了微科学与技术的发展，微纳尺度流动技术已成为其中重要的一个分支，如何准确、高效地获取相关流动参数，特别是通过实验手段获得整场、瞬态、高分辨率的流动参数与其演变过程已成为流体力学及其相关学科研究人员普遍关注的热点问题。作为流场速度测量中的一个重要手段，粒子图像/追踪测速技术得到了广泛的应用。其基本步骤如下：首先根据所得到的散焦图像进行二值化处理，得到可识别的散斑斑点，通过一定方法获取各散斑的准确位置，通过散斑间相互匹配确认该粒子在散斑图像中的位置特性，并根据该特性反向得到其在空间中的粒子位置，通过对所有散斑的识别即可得到该图中所有粒子的空间位置，最终通过两张图中粒子在空间位置的变化即可得到粒子在空间中的移动位移，从而得到粒子速度，继而反映出速度场的规律。

1散焦粒子图像测速技术原理

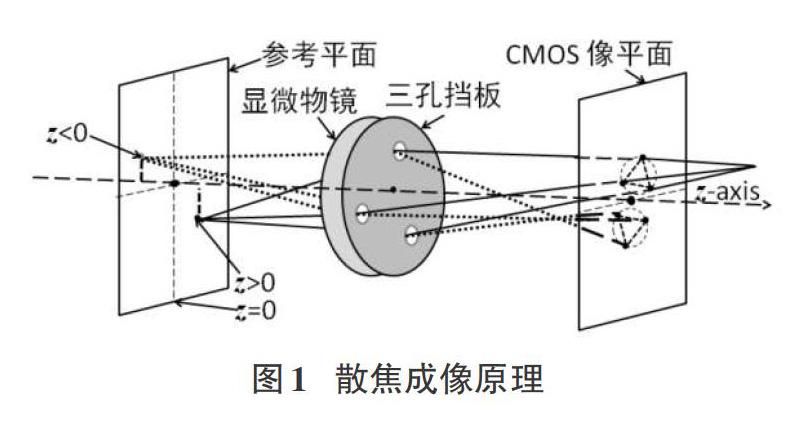
散焦粒子图像测速技术基本原理如图1所示。

由图1可知，不同位置及深度的粒子通过三孔挡板后在像平面上能生成不同的散斑图像，其散斑图像的位置反映实际粒子在其所在平面的位置，而散斑的大小反映其所在平面距离焦点处的距离，通过这种关系，当得到散斑图像后即可对应获得粒子的实际位置。

2相关算法实现

散焦粒子图像测速算法中首先需对图像进行二值化处理，其中主要有Otsu算法、自适应二值化算法以及快速自适应二值化算法等二值化处理方法。

散斑识别，可使用通过高斯掩模算法得到极点判断散斑质心，或直接套用圆霍夫变换获取质心，但散斑识别也存在难点，如斑点重合等。

散斑匹配，一组散斑其各散斑间角度往往固定，因此可基于此特点快速获得满足一定要求下符合其角度要求的一组散斑并匹配，且识别过程具有一定方向性，并对已匹配的散斑进行区别不接受其他匹配，保证匹配过程能快速进行。

位置标定，散斑位置、大小与相应粒子位置的需要通过实验具体测得。

粒子追踪匹，当得到两帧图像中粒子位置后，粒子匹配负责实现两帧中同一粒子的相互追踪匹配，通常使用最邻近法和松弛算法实现。其中最邻近法是指直接匹配两帧间最邻近粒子;而松弛算法指两帧间一定范围内以速度方向和大小大致相似为前提，通过多次迭代计算出最可能粒子匹配序列，并以此方式匹配粒子。

图2、图3为100对粒子绕原点旋转10。后通过两种追踪匹配算法获得的匹配图像。在100对粒子的匹配中使用松弛算法效果明显好于最邻近算法，虽然最邻近算法原理简单，但当粒子较为密集时该算法误匹配率较高，而松弛算法效果较好，但使用时参数较多，对于不同图片同时处理时可能出现参数相互不适应，同时参数选择不当时处理结果亦难以满足要求。

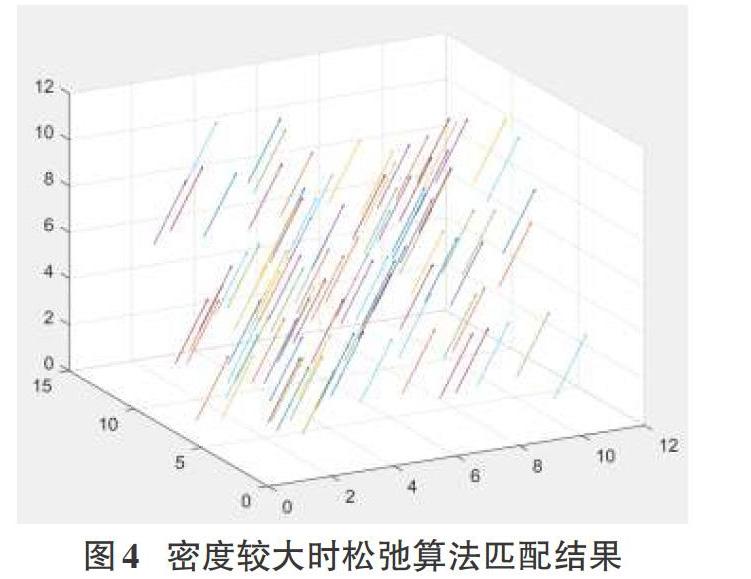
松弛算法可以使用在粒子密度较大的场合，且密度越大其匹配精度越高，并在匹配时能与周围粒子的匹配过程相互适应，可达到最终匹配一致的效果，图4为使用松弛算法的密度较大时粒子平移的匹配效果，由此可见，匹配精度较高。

3算法测试

首先，基于规则粒子群进行散斑图像生成并通过整套算法进行粒子追踪测速，粒子假定处于平面中心3cmx3cm方形区域内，间隔为0.5cm，平面深度为13-15cm处，平面相互间隔1cm，粒子绕中心旋转10°，其结果图5一图7所示：

由图7所示，规则粒子群使用松弛算法匹配成功率为100%，且位置判断较为准确，证明该算法可行。

然后使用随机分布的粒子群进行测试，散斑相较于规则粒子群而言会发生重合，造成散斑的识别困难，粒子较多时散斑识别及匹配准确性会明显下降。结果如图8所示。

由9图所示，使用松弛算法匹配得到的结果明显优于最邻近算法，且粒子越多结果正确率越高，但同时速度越慢，使用最邻近算法匹配结果误匹配率较高。

4结束语

分析表明，生成规则及不规则的粒子群在模拟旋转流动中的测试算法，其具体粒子群在以中心为原点进行旋转，生成散斑图像，并以图像为基础通过相应算法反向得到粒子位置及速度，从而实现对整体函数功能性的验证。实验表明使用最邻近法在各种规模的测试中最终效果均不如松弛算法，但使用松弛算法其参数较多且难以统一调试，造成了使用的不便。同时，散斑识别率均高于90%，可认为满足要求。