面向科研合作预测领域的作者相关度算法分析

单嵩岩，吴振新（1.中国科学院文献情报中心；2.中国科学院大学图书情报与档案管理系）

科学技术进步的关键是开放科学。开放科学是一种科学实践，使科学知识出版和传播越来越容易，让科学研究更具合作性和开放性。开放科学环境为科研人员提供了获取知识数据的多种途径，开放交流模型能够使科学人员更广泛、更便捷地寻求潜在的科研合作对象/团体，以促进学术传播。为了提供决策支持、便于科研人员选择合作者或团队成员，合作关系预测的研究变得越来越重要。科研预测领域的关键技术之一是作者相关性计算。虽然作者相关度研究已经取得了不错的进展，但随着新技术方法的不断引入，该研究还存在很大的进步空间。

1 科研合作预测领域的作者相关度研究概述

科研合作预测通常在学术论文构建的科研合作网络中进行，旨在预测从未合作过的作者在未来产生合作的可能性。作为社会网络的一种，科研合作网络体现了科研人员在文章或者研究项目中的合作关系，科研合作网络主要包括同构网络（如合著网络［1］） 和异构网络（如作者- 关键词网络［2］、作者- 文献网络［3］、作者- 文献- 术语- 会议网络［4］）。以合著网络为例，节点是作者，边是合著关系，合著网络中的合著关系预测就是计算尚未产生连边的作者节点对之间产生连边的可能性。合作网络的拓扑结构能够揭示作者之间未来合作的可能性，例如在合著网络中拥有共同同事、共同关键词以及研究内容相关的作者都有可能在未来展开合作。

在科研合作预测领域中，主要根据作者节点属性及网络的结构特征等信息（如相关人际关系、研究方向、兴趣等）计算作者间的相关度，并以相关度表示作者未来合作的可能性。在很多科研合作预测文章中，作者相关度也被称为相似度，在进行实际预测时，除了要衡量不同作者间的属性特征，更应关注不同作者在合作网络上是否近邻、是否属于同一知识社区。如，在合作网络中，两位拥有共同合作者但研究不同领域的作者，虽然属性特征相似度不高，但网络结构相似性高，则代表作者相关性大。

科研合作预测在本质上是一种链路预测，即通过已知的网络结构信息预测节点间未来产生连接的可能性，其中一类主流算法是基于节点相似性的方法。该方法根据已知网络中的作者节点拓扑结构，计算每一对未相连作者节点的结构相似度，相似度越高则其存在连边的概率越大，即作者未来合作的可能性更大。［5］科研合作预测研究早期基于同构网络（合著网络、引文网络等），采用多种节点拓扑相似性指标（如共同邻居指标、到达路径指标、随机游走指标）计算作者相关性。Liben-Nowell 和Kleinberg［2］率先将基于网络拓扑结构的多种节点相似性指数应用于社交网络链接预测，并在合著网络中进行了实验。周涛等在包括合著网络在内的多种现实网络中应用多种基于局部信息的指标实施链路预测，并另外提出两种指标：资源分配指标（RA） 和局部路径指标（LP）。［6］当前，越来越多的研究者采用相似度指标在合著网络中通过计算作者相关度来预测合作的可能性。文献［7］ 在7 门学科的合作网络中应用多种相似性指标进行链路预测。文献［8］ 运用多种相似度指标在合著网络中研究合作演化规律。

现实中，科研合作网络往往是异构的，同构网络节点相似性虽然易于计算，但却丢失了很多语义信息。传统的节点相似性指标无法直接应用到异构信息网络中，为了计算异构网络中的节点相似性，Sun 等于2011 年提出元路径的概念，并在异构书目网络中研究了合作关系预测问题。［9］随后，多种基于元路径的网络拓扑相似度指标相继被提出。文献［10］利用PathSim 算法在DBLP 文献数据集构成的“论文-作者-术语-会议”异构网络中寻找相关作者。文献［11］提出的HeteSim 算法度量异质网络中任意节点对的相关性，在ACM（“机构- 作者- 论文- 术语- 学科-会议-出版物”异构网络）和DBLP 数据集上计算作者节点相关度。文献［12］提出了一种基于元路径的新型相似性度量算法AvgSim，并在ACM 数据集和DBLP 数据集上计算作者节点相关度。文献［13］ 在APS（“论文- 作者- 机构- 术语- 学科- 期刊- 年刊”异构网络）和DBLP 数据集上，基于时间动态的路径数、传递相似性的归一化路径数和作者属性的对称随机游走计算作者节点间的相关性。

传统链路预测方法使用的网络拓扑相似性指标普遍存在计算效率较低和数据稀疏造成的维数过高问题，很难应用于大规模数据集的科研合作网络进行合作预测。随着表示学习的不断发展，新兴的网络表示学习方法能够将节点表示成向量，通过计算向量相似度获得节点相似度。该方法可以高效计算网络中节点间的语义联系，也能够解决数据稀疏下的语义关联抽取和计算复杂问题，［14］因此学者们也尝试将新方法应用于合作预测。张金柱等利用LINE 网络表示学习方法对作者向量进行表示学习，并通过向量夹角余弦值计算作者间的语义相似度。［14］文献［15］ 提出了LINE 算法并在合著网络中进行了实验，在识别相关作者中取得了良好的效果。文献［16］构建论文- 期刊-作者异构网络，以作者为中心，结合元路径应用Node2vec 模型得到作者的向量表示，根据明可夫斯基距离、余弦值计算他们之间的向量相似度。文献［17］提出metapath2vec 表示学习方法，并在作者-论文-会议异构网络中进行了相关作者聚类实验。

2 基于网络拓扑结构相似度的作者相关度算法分析和比较

基于相似性的方法在科研合作网络上进行合作预测，需要选取作者节点的拓扑信息，利用合著、引用、同属一个机构等连边的语义信息计算作者间的相关性，即利用拓扑相似度算法计算作者网络信息的相似程度。

2.1 基于同构网络节点相似性指标的作者相关度计算

基于网络拓扑结构相似度衡量作者间的相关度，是将作者实体间的关系连结起来构成网络图，利用图中节点间的连接属性判定两个作者的相关性。

采用节点拓扑相似性指标计算同构网络（合著网络）中作者节点的相关性，相似性指标包括基于邻居的度量（网络局部结构的相似性）、基于路径的度量（准局部结构的相似性）、基于随机游走的度量（网络全局结构的相似性）。这里的“相似性”是指相关文献已成习惯的术语, 实际上很多相似性指标衡量的并非是节点对是否具有相似的特征, 而是节点对在几何或者拓扑空间是否邻近, 或者在功能上是否具有较大的关联，［18］因此也被称为“接近性”或“相关性”。最简单的相似性指标是共同邻居，两个节点如果有更多的共同邻居就可能更相似。基于路径思想的相似性算法考虑到使用共同邻居指标进行计算时，相似性分数可能分布过于集中，使得预测结果没有区分度，所以将两个节点的共同邻居扩展到“n 阶共同邻居”。［7］基于随机游走的思想是利用一个节点到其邻居的转移概率来描述当前节点随机游走的目的地，可以根据整个网络图的信息来计算节点相似度，即使两个节点之间没有公共邻居节点也能计算。

拓扑相似性指标只涉及网络的结构信息。相似性指标计算起来比较简单，但不同指标在不同网络中的预测能力却不一致，其预测的精确度取决于对网络结构特征刻画的好坏。［19］在合著网络中，基于邻居和路径的相似性指标在识别作者相关度时表现良好，尤其是共同邻居指标、Adamic/Adar 指标、资源分配指标（RA）和Katz 指标（见表1）。

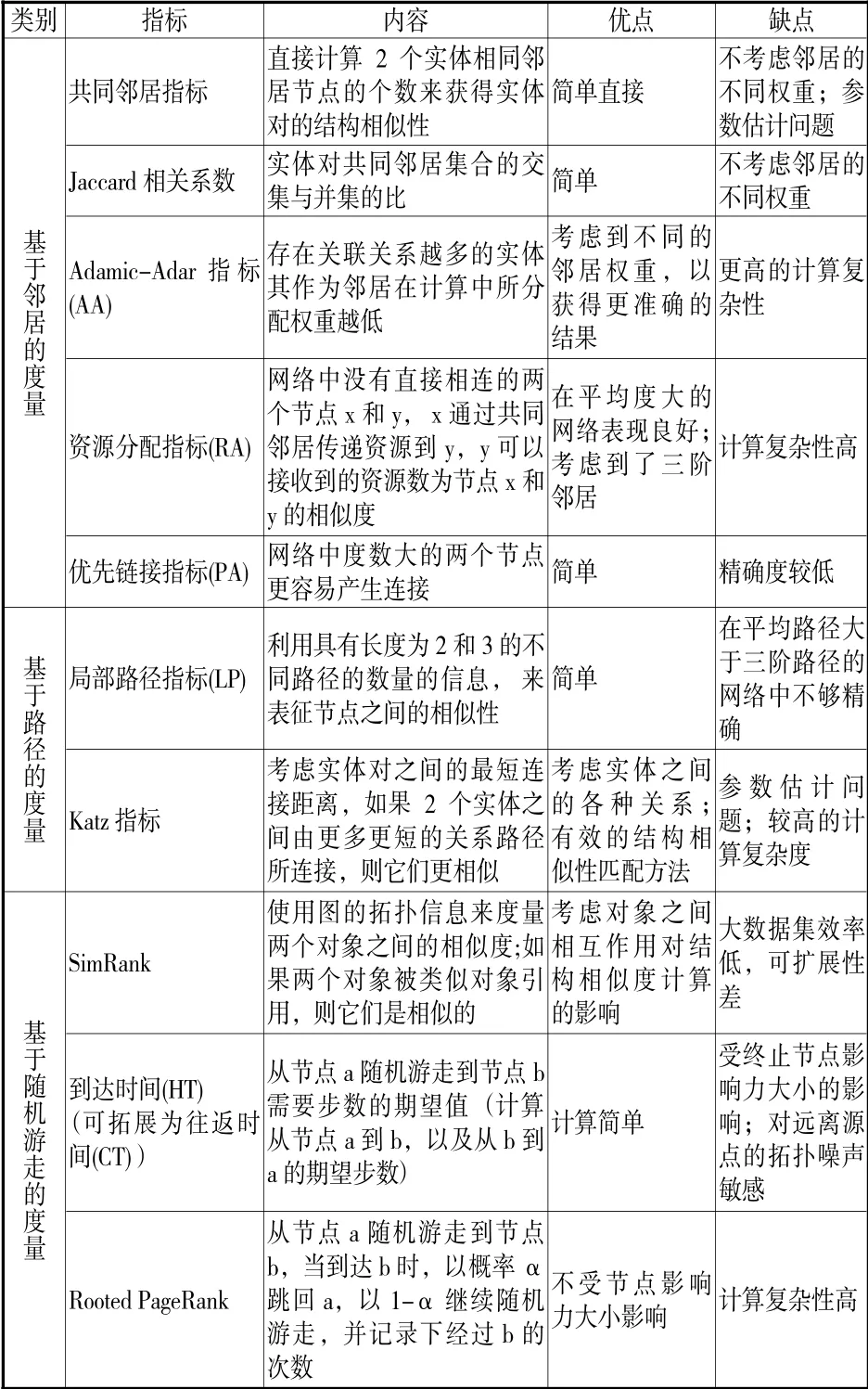
表1 代表性节点拓扑相似度指标

合作关系所形成的合著网络是一个熟人网络，共同邻居指标能很好地衡量两位作者的直接合作者，Katz 指标能很好地衡量两位作者的间接合作者。Adamic/Adar 指标、资源分配指标（RA） 是改进指标，赋予度小的共同邻居节点更大的权重，因为度小的作者选择的合作者与其相关性更高。在多种研究领域内，PA 指标往往表现一般，因为度大的作者（即影响力大的作者）合作概率小。［2,7,8,19］

2.2 基于异构网络的元路径拓扑相似度指标的作者相关度计算

科研合作网络通常是异构的，即网络中存在多种类型的节点或连边。同构网络是异构网络的投影，如合著网络就是由文献-作者网络投影形成的，虽然合著网络易于计算分析，但失去了原异构科研合作网络中丰富的语义信息。近年来，学者通过异构网络来解决科研合作预测问题，主要采取基于元路径的方法。元路径是定义在网络模式上的，用于描述异构网络中组合关系的路径。不同的元路径用不同的语义来描述节点之间的相似程度。依据不同元路径的路径，可以将同构网络中基于邻居和路径的属性拓展到异构信息网络中。例如，当区别看待不同类型的邻居节点并且把一阶邻居扩展为n 阶邻居（某一节点和它的邻居之间的距离为n）时，则两个作者间的共同邻居属性就变成两个作者之间依据不同元路径的路径数目。［16］

基于元路径的相似性计算首先使用元路径定义两个节点之间的拓扑结构，然后在具体的拓扑上定义不同的度量标准。该方法考虑异构信息网络中不同拓扑结构的丰富语义信息和形成原因来进行计算。如包含作者（A）、论文（P）、出版物（V） 三种节点的合作异构网络，两个作者节点间的元路径有2 种：A1-P1-V1-P2-A2 代表A1 和A2 在同一出版物上发表过文章，A1-P1→P2-A2 代表A1 的论文P1 引用了A2 的论文P2。

在元路径相似度指标中，以路径数和随机游走为基础的相似性度量适用于具有高出入度的对象，基于成对的随机游走的相似性度量适用于集中的对象（即大部分的链接属于小部分节点）。［10］在科研合作异构网络中，连接两个作者之间的元路径越多，两者越相关，归一化路径数指标往往能取得良好的效果。［9］表示两位作者拥有共同合作者、在同一出版物上发表论文、研究相关领域和引用相同论文的元路径，均在识别作者相关度中发挥了重要作用。虽然越长的元路径携带的信息越多，但随着元路径长度的增加，算法也越来越复杂，但精度增长幅度不大，因此长度一般控制在6 个节点以内（见表2）。

2.3 基于新兴网络表示学习方法的作者相关度计算

随着表示学习的发展，除了在科研合作网络中采用结构相似性指标计算作者节点相关度，基于深度学习的网络表示学习方法也得到了广泛应用。网络表示学习方法将图中的节点表示成低维、实值、稠密的向量形式，通过计算向量间的距离判断节点的相关性。

基于神经语言模型的网络表示学习是目前的研究热点，其基本原理和思路来源于代表性的词向量生成工具Word2Vec。［20］Word2Vec 工具包含CBOW 模型和Skip-gram 模型，选取输入词的前后n 个词作为上下文，学习包含语义信息的输入词的向量表示。针对网络结构和神经语言模型的特点，网络表示学习把节点类比为词，把在网络中获得的节点序列类比为句子，将节点序列作为Word2Vec 的输入，根据每个节点的上下文信息，得到节点的向量表示。根据节点序列获取 方 式 的 不 同，形成 了 以DeepWalk［21］、LINE［15］、Node2vec［22］、Metapath2Vec［17］等为代表的基于神经语言模型的网络表示学习方法（见表3）。

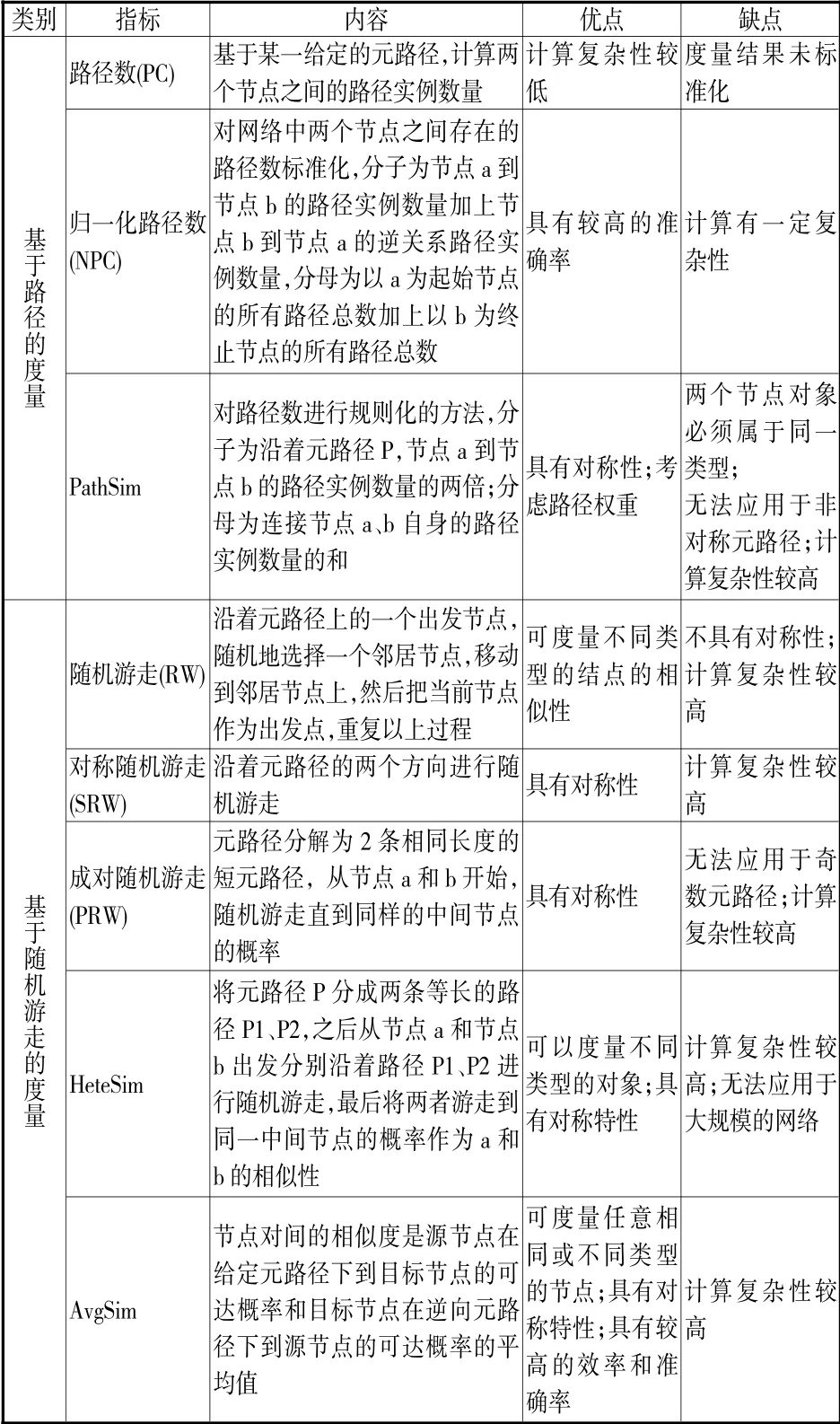
表2 代表性元路径相似度指标

在科研合作网络中，利用网络表示学习方法预测科研合作，根据上下文语境得到每位作者的向量表示，将合作预测变为作者向量相似度计算问题，相似度越高的未合作过的作者越有可能进行合作。

网络表示学习为复杂网络分析提供了新的视角，一部分研究者开始探索将其应用到科研合作网络。在合著网络中，DeepWalk、LINE、Node2vec 都能取得不错的效果，其中Node2vec 表现更好，DeepWalk 更适合稀疏网络，LINE 更适合大规模网络。Metapath2Vec在科研合作异构网络中计算作者相关度方面取得了良好的效果。［15,17,22］网络表示学习能在大规模数据集中自动提取合作网络中作者关联语义，在计算作者相关度方面有广阔的研究应用空间。

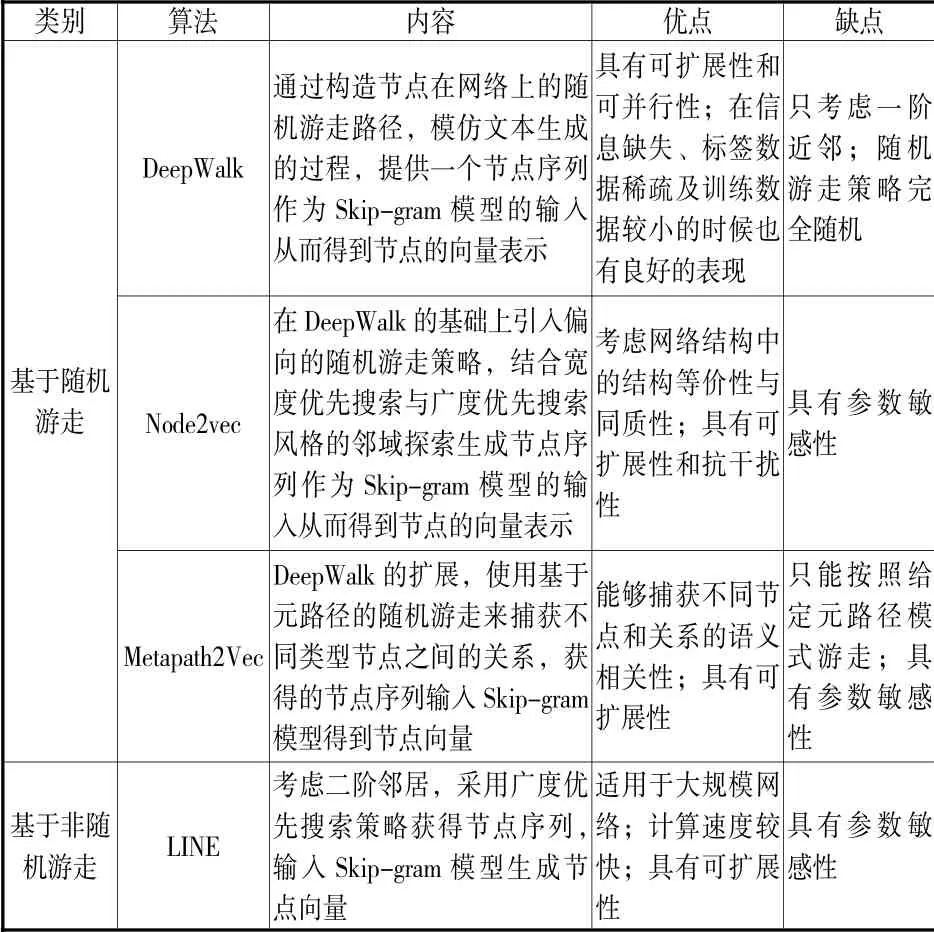
表3 基于神经语言模型的网络表示学习代表性算法

3 结语

在合作预测领域，作者相关度计算方法的研究发展紧跟新兴技术发展步伐。通过科研合作网络结构信息判断作者相关性，经历了从同构网络到异构网络的发展，日益精细化、精准化。

（1）网络表示学习方法将在作者相关度计算中得到进一步应用。随着词向量在文本相似度计算上的成功，涌现出一批借鉴语言模型完成的网络/图表示学习的方法已在合作网络中尝试应用，那么其他基于深度学习的网络表示学习方法能否有更好的表现，以及网络中其他结构的表示（如子图向量、图向量）能否应用到作者相关度计算仍需进一步探索。

（2）构建科技知识图谱能为作者相关度计算提供更多支持。与简单的科研合作网络（如合著网络、二分网络、三种节点网络等）相比，构建拥有更全面的作者及相关实体节点、更丰富的作者语义信息的科技知识图谱，能够更全面地比较作者间相关性，在知识图谱中寻找相关作者也将有更多应用场景。