基于神经网络PID综掘巷道超前支架支撑力自适应控制
2019-12-16薛光辉柴敬轩瞿圆媛
薛光辉,管 健,柴敬轩,张 昊,瞿圆媛,吴 淼
(中国矿业大学(北京)机电与信息工程学院,北京 100083)
随着煤炭开采深度的增加,综掘工作面面临着高地应力等复杂问题。在掘进扰动作用下,巷道围岩会出现大范围塑性变形破坏并伴随大量级、大规模的强烈动力失稳等严重现象[1-4],严重威胁着工作面煤矿工人的人身安全,其围岩控制与超前支护问题尤为重要。研究表明,在巷道掘进过程中,围岩压力不断变化且呈一定规律性,巷道围岩本身也具有一定的自承能力[5-6],为避免巷道围岩出现破裂、碎裂等现象,超前支架的支撑力应能够自适应围岩的压力,实现综掘工作面的安全临时支护。
近几年,国内外学者在深部围岩压力变化规律、支架失稳机理与控制和神经网络PID控制方面开展了许多研究。薛光辉等[7-9]利用FLAC3D软件仿真分析了深部围岩压力及其对超前支架的影响,提出了一种新型综掘巷道超前支架,对支架的支护性能进行了分析,并讨论了其工作阻力的确定方法。何勇等[10]研究了迈步式超前支护液压支架立柱进行控制的问题。王国法等[11-13]研究了千米深井围岩控制及智能开采、煤炭智能开采关键技术、液压支架与围岩的耦合关系。杨科等[14]研究了大倾角煤层综采工作面液压支架失稳机理及其控制,通过支架让压来实现对顶板压力的自适应。栾丽君等、卢进南等[15-16]研究了综掘巷道迈步式超前支架的电液伺服位置压力复合控制策略及多缸同步控制策略。王保勤[17]研究了临时支架液压同步系统的多缸同步控制问题。CAO L M等[18]针对采煤工作面液压支架推进控制系统,仿真分析了其液压阀芯位移曲线和推进执行器流量曲线。李明等[19]使用神经网络PID对伺服电机进行控制,提高了系统的自适应能力和鲁棒性。KINOSHITA等[20]使用神经网络PID对坦克系统液位进行了控制,证明了该算法的有效性。
综上,由于对巷道围岩变形机理及支架控制系统的非线性问题认识不足,支架支撑力自适应控制的研究尚处于探索阶段。神经网络具有能够逼近任意非线性系统的优点[21],可对PID参数进行实时调整,以达到自适应的目的。笔者利用神经网络PID理论研究所设计超前支架的支撑力自适应控制问题,使其能够自动适应顶板的压力变化,以避免因支架出力过大导致巷道围岩的破裂。
1 自移式超前支架支撑力控制系统及其数学模型
1.1 自移式超前支架及支撑力控制系统
自移式超前支架[7]总体结构如图1所示,由顶梁、伸缩梁、护帮板、底座、护帮千斤顶、顶梁千斤顶和立柱等组成。顶梁与伸缩梁通过液压缸连接。护帮板与护帮千斤顶通过铰接连接。立柱与伸缩梁通过球副铰接连接,与底座通过铰接连接。

图1 超前支架总体结构示意
超前支架立柱油缸的液压控制系统图如图2所示,由油箱、乳化液泵、滤油器、电液伺服阀、单向阀、安全阀、液压缸、压力传感器、控制器和伺服放大器等组成,其中,P为立柱液压缸压力输出;F为压力传感器输出;MOT为电机;“+”表示该支路输入为正;“-”表示该支路输入量为负。

图2 超前支架液压控制系统
支架由乳化液泵站供液。支架顶梁中心安装有压力传感器,以监测巷道围岩的压力。超前支架的支撑力由安装在立柱液压缸回路中的压力传感器来获取。超前支架支撑力自适应控制过程为:乳化液经滤油器、乳化液泵、单向阀、电液伺服阀进入支架立柱液压缸下腔,立柱上升;当支架与顶板接触后,立柱液压缸内乳化液压力不断升高,以顶板压力传感器测得的顶板压力和油路压力传感器测得的支架支撑力作为控制器的输入,经控制器计算后,输出信号经伺服放大器放大后,调节电液伺服阀的开口大小及方向,使得支架输出支撑力跟踪顶板压力,实现支架支撑力自适应控制,控制系统原理框图如图3所示。

图3 超前支架控制系统原理框
图3中,r为顶板压力传感器测得的围岩压力;y为支架立柱压力传感器测得的支撑力;e为围岩压力r与支架输出支撑力y的偏差;de为偏差e的变化率。以r,y,e,de作为神经网络PID控制器的输入,经神经网络运算后得到Kp,Ki和Kd输入PID控制器,产生的控制信号经伺服放大器放大后控制电液伺服阀,进而控制进入液压缸的流量,使得立柱输出支撑力y随围岩压力r变化,实现支架支撑力的自适应控制,其中,Kp,Ki和Kd为PID的3个参量,即比例系数、积分系数和微分系数。
1.2 控制系统数学模型
假定阀和液压缸的连接管道对称且短粗,管道动态与管中压力损失可以忽略;液压缸各工作腔内各处压力相等,油温、体积弹性模量是常数;液压缸内、外泄漏均为层流流动[22],则有
伺服阀流量方程:
QL=kqxv-kcpL
(1)
式中,QL为液压缸输入流量,m3/s;kq为伺服阀流量增益,L/(min·m);kc为阀门压力,MPa;xv为阀芯位移,m;pL为供油压力,MPa。
液压缸流量连续性方程:
(2)
式中,Ap为液压缸有效工作面积,cm2;s为拉普拉斯变量;xp为立柱油缸活塞位移;Cip为液压缸总泄露系数,L/(min·MPa);Vt为系统总压缩体积系数;βe为液压油弹性模量,Pa。
液压缸力平衡方程:
Fg=AppL=Mts2xp+Bpsxp+KSXp
(3)
式中,Mt为负载质量,kg;Bp为负载阻尼系数,(N·s)/m;KS为负载弹簧刚度,N/m。
由式(1)~(3)得到阀控液压缸的传递函数Gp(s)为
Gp(s)=
(4)
假设系统无弹性负载,上式可简化为
(5)
式中,Fg为阀控液压缸所承受的负载;kce=kc+Cip,L/(min·MPa);ωm为负载的固有频率,Hz;ωr为液压弹簧与负载弹簧串联耦合的刚度与阻尼系数之比,Hz;ω0为液压弹簧与负载弹簧并联耦合的刚度与负载质量形成的固有频率,Hz;ξ0为阻尼比。
电液伺服阀的传递函数为二阶振荡环节形式,即
(6)
式中,GSV为电液伺服阀的传递函数;ΔI为电液伺服阀输入电流变化量;KSV为伺服阀流量增益,L/(min·m);ωSV为伺服阀固有频率,Hz;ζSV为伺服阀阻尼比。
伺服放大器的传递函数为
(7)
式中,I(s)为伺服放大器输出电流,A;U(s)为伺服放大器输入电压,V。
压力传感器的传递函数为
(8)
式中,U(s)为压力传感器输出电压,V;Fg为液压缸输出压力,N。
综合上述各式,可推导出超前支架支撑力控制系统开环传递函数为
(9)
2 神经网络PID
2.1 BP神经网络
神经网络是一种仿生式模型,在一定程度上受到了人脑神经网络的启发[23]。神经网络分为输入层、隐含层和输出层3个部分组成。图4为3层BP网络的结构图。信号由输入层进入神经网络,由左向右依次传播,直至输出层,网络的层间是全连接。
输入层的输入为

隐含层输入、输出为
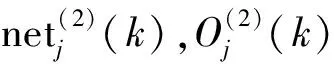

图4 BP神经网络结构
输出层的输入、输出为

取性能指标:
依最速下降法修正网络的权系数,并附加一使搜索快速收敛到全局极小的惯性项,则
式中,λ为学习速率;η为惯性系数。
由于∂y(k)/∂u(k)未知,所以近似用符号函数sgn(∂y(k)/∂u(k))代替,由此计算不确定的影响可以通过调整学习速率λ来补偿。
根据经典增量式数字PID的控制算法:
u(k)=u(k-1)+Kp[e(k)-e(k-1)]+
Kie(k)+Kd[e(k)-2e(k-1)+e(k-2)]
式中,J为性能指标函数;r(k)为k时刻顶板压力;y(k)为k时刻液压支架(立柱油缸)输出压力;u(k)为k时刻支架立柱油缸输入;e(k)为k时刻顶板压力r(k)与液压支架输出压力y(k)的差。
可得:
因此,可得神经网络输出层权系数计算公式为

(10)
其中,
q=1,2,3
g′(x)=g(x)(1-g(x))
从而,计算隐含层权系数如下:
(11)
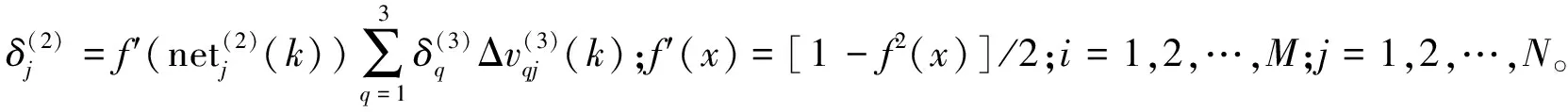
2.2 基于BP网络的PID控制器
该控制器控制算法如下:
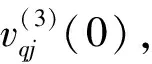
(2)给定r(k),y(k),计算此时刻误差e(k)=r(k)-y(k)及误差的微分de(k)=[e(k)-e(k-1)]/T,其中T是每一次循环经历的时间。
(3)将r(k),y(k),e(k)和de(k)作为输入,代入神经网络模型中,计算神经网络各层神经元的输入、输出,输出层的输出即为PID控制器的3个可调参数Kp,Ki,Kd。
(4)计算PID控制器的输出u(k)。
(6)令k=k+1,返回到第(2)步。
3 超前支架支撑力控制系统性能分析
3.1 控制系统性能
根据支架下端立柱内径130 mm,上端立柱内径80 mm,计算得到kq=27 000 L/(min·m),kce=0.06 L/(min·MPa),Ap=84.425 cm2,ωm=59 Hz,ωr=0.13 rad/s,ω0=842.5 Hz,ξ0=0.15,KSV=0.056 L/(min·m),ωSV=110 Hz,ζSV=0.7,取伺服放大器增益Kp=0.007 A/V,压力传感器增益KS=100 V/N,代入式(9),利用Matlab仿真得到超前支架支撑力控制系统的Bode图和Nyquist图,如图5所示,其中,Gm为幅值裕度;Pm为相位裕度。

图5 超前支架支撑力控制系统性能曲线
由图5可知,系统具有负相角裕度和负幅值裕度,需要加入校正环节使系统稳定。
3.2 PID控制
在超前支架支撑力控制系统中,引入PID控制后,系统的单位阶跃响应如图6中蓝色曲线所示。由图6可知,系统稳定,但调节时间过长。
3.3 神经网络PID控制
为改善系统的动态性能,采用神经网络来整定PID控制参数。采用4-5-3的神经网络结构模型,网络输入层节点数为4,分别对应r(k),y(k),e(k)和de(k),隐含层节点数为5,输出层节点数为3,分别为对应的PID控制参数,隐含层激活函数采用双曲正切函数,输出层激活函数采用Sigmoid函数,根据仿真效果选取学习速率为100,惯性系数为0.05,仿真得到的系统单位阶跃响应如图6红色曲线所示。
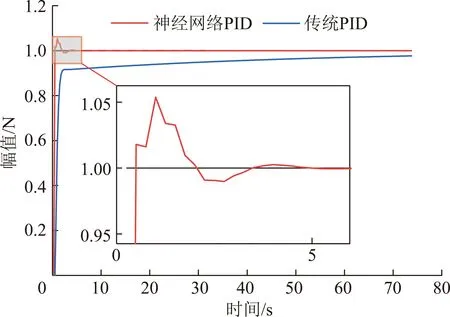
图6 引入控制算法后支架支撑力控制系统单位阶跃响应
对比可知,引入神经网络PID后,系统的动态性能得到了很大改善,调节时间由约32 s缩短为约2 s,缩短了约16倍,出现了约6%超调。
4 仿真试验
4.1 围岩压力曲线
根据实测的旗山矿的地质条件,见表1,在FLAC3D中建立了围岩-超前支架力学耦合模型[7],仿真计算得到了围岩顶板的压力随时间的变化规律,如图7所示。由图7可知,围岩顶板压力呈周期性波动,且波动较大,若支架支撑力不能跟随顶板压力变化而做出调整,则可能导致顶板被破坏,且对支架寿命也有影响。
表1 旗山矿地质条件及其力学参数[3]
Table 1 Geological conditions and mechanical parameters in Qishan coal mine[3]
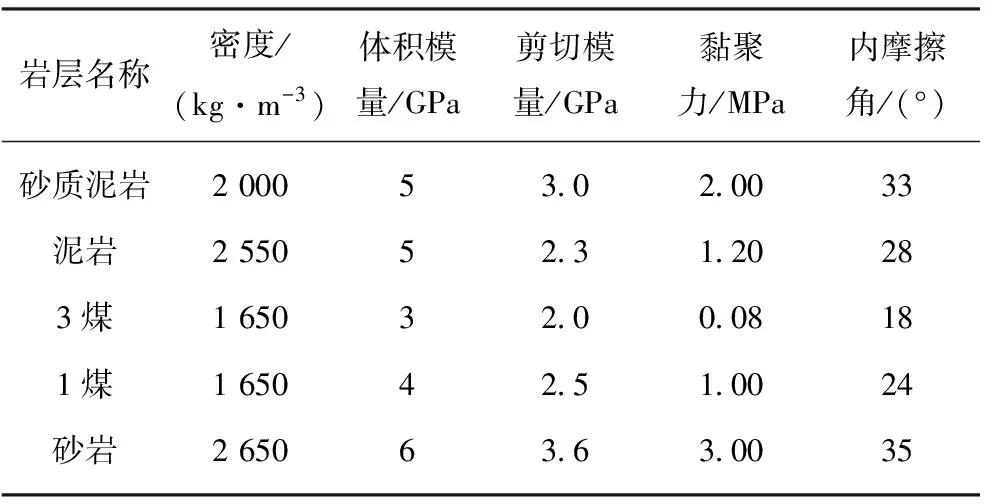
岩层名称密度/(kg·m-3)体积模量/GPa剪切模量/GPa黏聚力/MPa内摩擦角/(°)砂质泥岩200053.02.0033泥岩255052.31.20283煤165032.00.08181煤165042.51.0024砂岩265063.63.0035
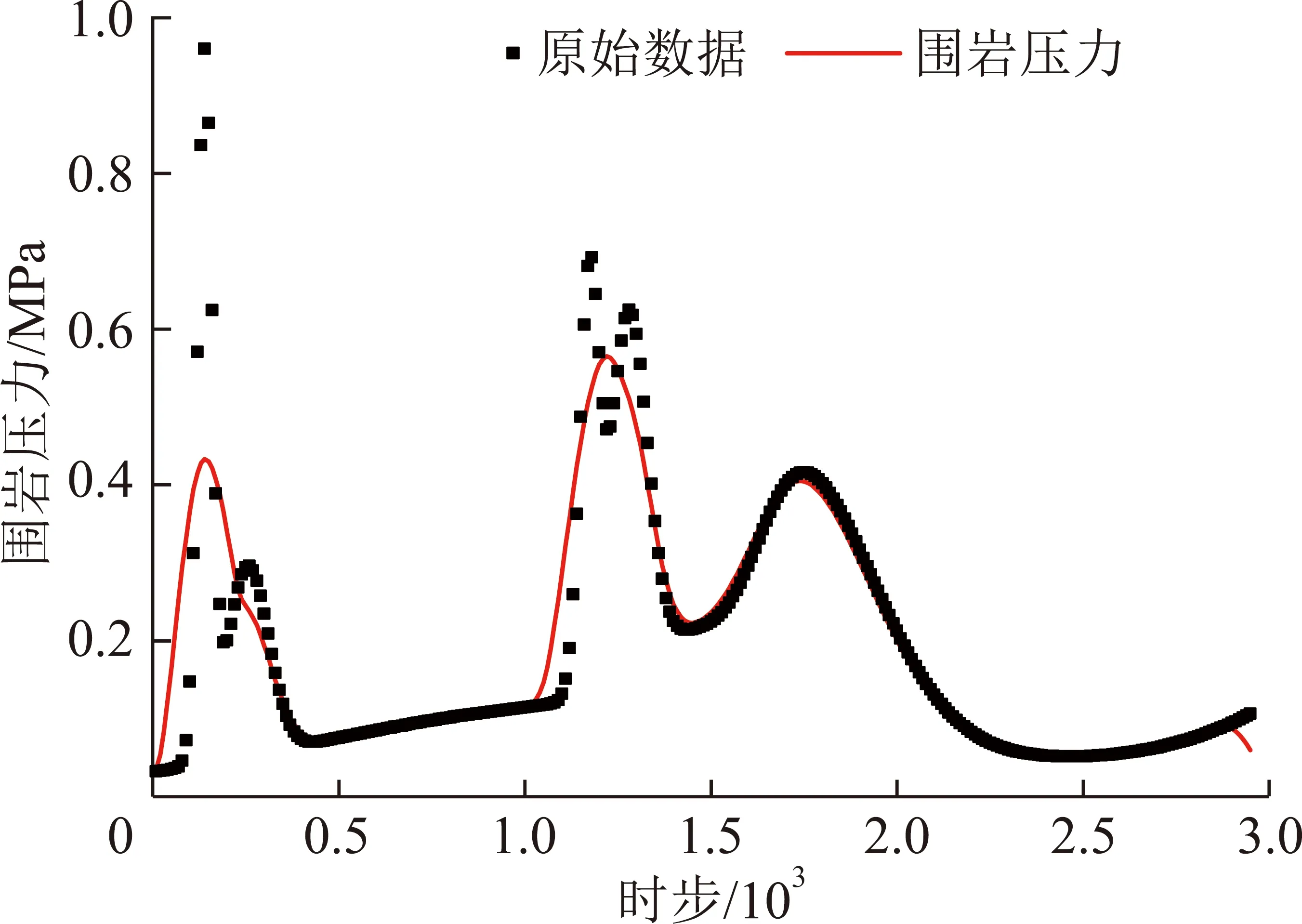
图7 仿真得到的旗山矿围岩压力变化曲线

图8 超前支架支撑力自适应控制系统仿真实验结果
4.2 自适应仿真试验
以围岩顶板压力曲线作为输入,仿真分析了超前支架支撑力自适应控制系统,结果如图8所示。由图8可知,与传统PID控制相比,采用神经网络PID控制后,支架支撑力控制系统对围岩顶板压力的跟踪性能好。
图9为基于2种控制算法的围岩压力自适应跟踪误差曲线。由图9可知,采用神经网络PID控制策略的跟踪误差比传统PID的误差小,跟踪效果具有明显优势。采用神经网络PID控制策略时,支架支撑力自适应控制系统跟随围岩压力曲线的误差为0.005 5,而传统PID控制的误差为0.037 4,改善了约6.8倍。
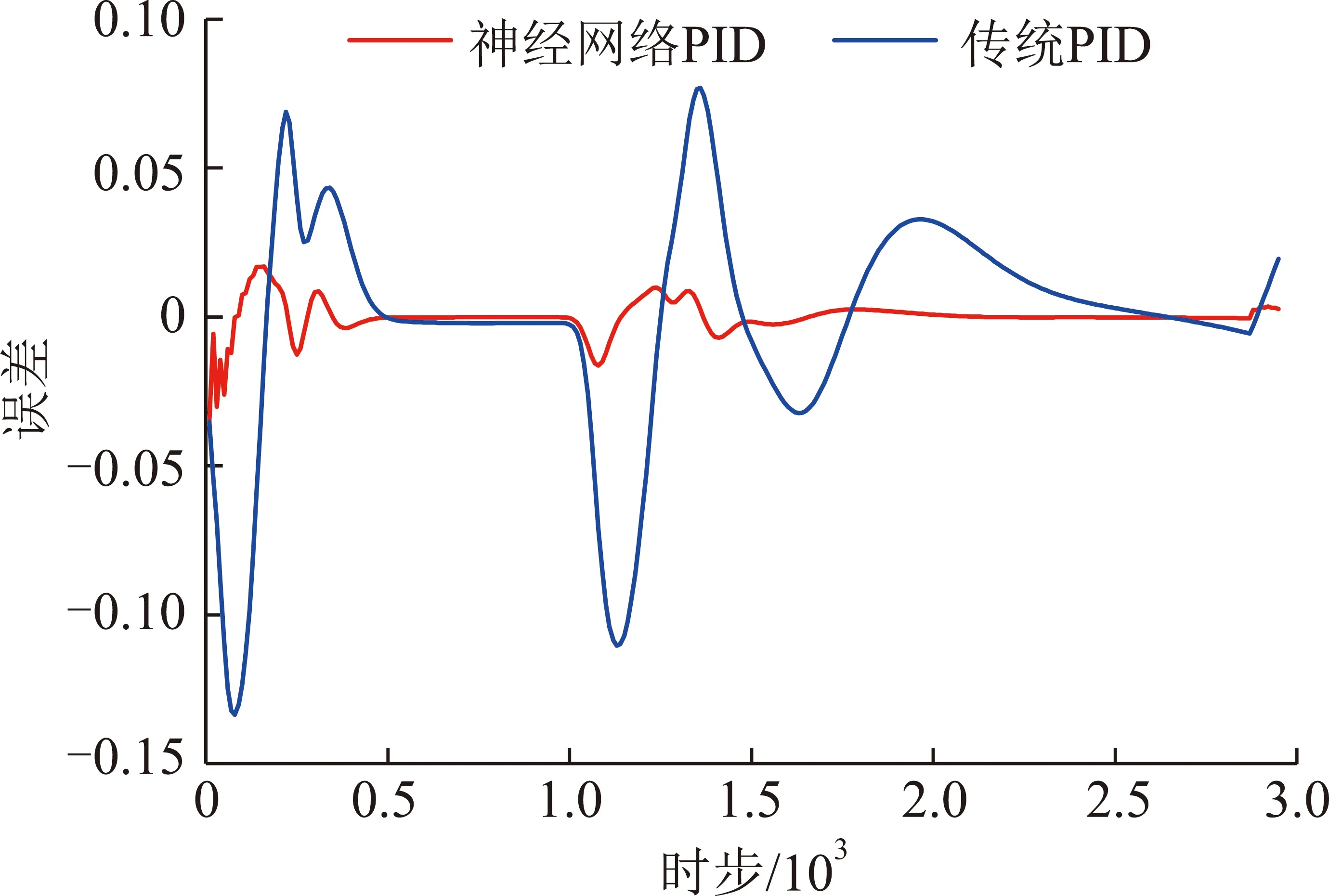
图9 基于2种控制算法的围岩压力自适应跟踪误差曲线
图10为采用神经网络PID控制策略时,超前支架支撑力自适应控制系统归一化后的PID参数变化曲线。由图10可知,随着巷道围岩压力变化,神经网络不断调整PID参数,使得支架支撑力快速跟随围岩压力变化。

图10 超前支架支撑力自适应控制系统归一化后PID参数变化
由此可知,神经网络PID控制时跟踪效果优势明显和较小的跟踪误差得益于在控制过程中神经网络PID控制策略能实时调节PID参数。当误差较大或较小时,神经网络能够自适应调节PID参数至合适的值,收敛速度更快,从而使支架支撑力跟踪围岩压力效果更好,跟踪误差更小。
5 结 论
(1)提出了一种新型自移式综掘巷道超前支架,分析了自移式超前支架的结构,提出了支架支撑力自适应控制液压系统,阐述了其工作原理和过程,建立了该控制系统的数学模型。
(2)改变了传统液压支架工作原理,运用神经网络PID控制策略对超前支架支撑力进行自适应控制,分析了系统的性能,结果表明引入神经网络PID控制算法后,支架支撑力控制系统调节时间比传统PID控制策略缩短了约16倍,动态性能得到了改善。
(3)仿真计算得到了旗山矿围岩压力变化曲线,分析了支架支撑力自适应控制系统对围岩压力曲线的自适应情况,结果表明采用神经网络整定PID参数后,支架支撑力自适应控制系统跟随围岩压力曲线的误差为0.005 5,传统PID控制的误差为0.037 4,改善了约6.8倍。
