气源岩吸附试验的机理及吸附特征新认识

2019-12-16张玉贵贾天让钟福平

煤炭学报 2019年11期

刘操,张玉贵,4,贾天让,钟福平

(1.河南理工大学安全科学与工程学院,河南焦作 454003; 2.河南理工大学河南省瓦斯地质与瓦斯治理重点实验室-省部共建国家重点实验室培育基地，河南焦作 454000; 3.全国煤炭行业瓦斯地质与瓦斯防治工程研究中心，河南焦作 454003; 4.中原经济区煤层(页岩)气河南省协同创新中心，河南焦作 454000)

我国煤层气和页岩气开发近年来得到了长足发展和持续增产，因为煤层气和页岩气赋存在富含有机质的煤、页岩等气源岩储层中，其主要成分为甲烷，所以在实验室测试甲烷在气源岩中的吸附、解吸和扩散渗流等物理特性变成了矿井瓦斯抽采、煤与瓦斯突出防治和页岩气开发等领域的研究热点。甲烷在气源岩储层中主要以游离相和吸附相赋存[1]，其中绝大多数以吸附相的形式存在，研究表明页岩气中的吸附相资源量约为15%～80%[2]，煤层气中的吸附相资源量超过80%[3]。因此，要掌握各开采气田中的煤层气和页岩气的储量、气含量、产量和可持续开采能力等基础指标，首先得准确掌握煤、页岩等气源岩的吸附能力和吸附特征。

当前，国内外学者普遍采用体积法或者重量法在实验室测试气源岩的吸附量[4]，并建立吸附等温线预测和理解气源岩的吸附能力、吸附特性和吸附机制，大量的实验室试验测试出了两类特征迥异的吸附等温线:一类是先上升至饱和吸附能力后形成直线平台的Langmuir型等温线[1,5-14]，另一类是先上升后下降具有峰值特征的等温线[15-25](以下简称“峰值”型等温线)。然而，这两类吸附等温线却存在着理论解释上的争议和实践应用上的误差风险:

第1，理论解释方面，可归纳为4种具有争议性的吸附类型:① Langmuir型吸附。经典观点认为气源岩吸附遵循Langmuir模型，吸附等温线是IUPAC[14]所划分的第Ⅰ类等温线，富含有机质的煤体或者页岩表面完全覆盖一层气体后即达到饱和吸附压力，此后，无论怎么增加吸附压力，吸附量不再增加。② 负吸附。聂海宽等将[20,23-25]试验测试的低阶煤和页岩的“峰值”型吸附等温线称为“负吸附”现象，原因是随着吸附压力增大，页岩和煤中可供瓦斯吸附的表面积是降低的，页岩和煤的真实吸附能力是降低的。③ 解吸滞后型吸附。琚宜文等[16,21]学者认为构造煤中的吸附先进行一段时间后才开始解吸，因此造成随着吸附压力升高吸附量下降的“峰值”型特征。④ 超临界吸附。侯晓伟与沈瑞等[20,22]学者将“峰值”型吸附等温线解释为超临界吸附具有阶段性，候晓伟等[20]认为页岩吸附可以分为初始吸附、超临界吸附“瓶颈”、饱和吸附和负吸附4个阶段;沈瑞等[22]认为页岩吸附存在超临界饱和解吸压力，只有达到了该压力才发生吸附气的解吸附。

第2，实践应用方面，很多学者和工程人员[15,26-28]采用Langmuir模型拟合吸附等温线求出吸附常数(煤炭行业习惯称为a,b值，部分行业习惯将a值称为朗格缪尔体积、b值的倒数称为朗格缪尔压力)，并以朗格缪尔体积作为气源岩的饱和吸附量，进一步开展气源岩吸附模型精度比对[15]、页岩的吸附解吸特征[26]和热力学[27]、煤层气和页岩气资源量计算、煤矿瓦斯防治和瓦斯抽采的基础参数[28]、突出变形煤吸附特性[7,29-30]等理论和工程实践研究。然而，上述争议的吸附类型和“峰值”型吸附特征的等温线完全不符合Langmuir模型，普遍采用Langmuir模型拟合这些非Langmuir型等温线，不但得出了错误的吸附常数，而且给煤层突出危险性评估、煤矿瓦斯治理和页岩气资源量评估等工程实践和气源岩的吸附解吸机理研究带来极大的误差风险。

笔者针对上述争议和误差风险，首先建立了基于吸附相的吸附试验模型，从吸附试验机理上证实:实验室测试的吸附等温线只能是“峰值”型而不可能是Langmuir型，“峰值”型吸附等温线下降的机理是吸附试验原理中省略了Gibbs舍弃量[4]，而不是上述争议的吸附类型。然后以平顶山八矿肥煤为例，使用体积法试验测试了4条等温线，并采用液相法、截距法和Langmuir模型法等多种方法校正得出了实际吸附量等温线，结果表明:仅截距法校正的实际吸附量等温线符合饱和吸附的物理特征，而常用的液相法、Langmuir模型法误差很大。

1 理论

1.1 吸附试验机理

吸附相的概念最早是吉布斯(Gibbs)研究表面吸附时提出的，如图1所示，任何一个固、气吸附实验系统都可以简化为3部分:吸附剂、吸附相和游离相。系统中的吸附相因吸附力的作用可沿吸附剂表面扩大一定距离并占用一定体积va，吸附相的密度ρa不是均一的，而是距离吸附剂表面越近密度越高，距离吸附剂表面越远越趋于与游离相浓度或者说游离气体浓度ρ平衡。然而，依靠当今的科技手段吸附相和游离相的界面是无法分离的(图1)，因此无法准确得出吸附相的物质量—实际吸附量ma究竟是多少。为了克服这个困难，Gibbs将吸附相分为两部分:Gibbs表面过剩吸附量me(以下简称Gibbs吸附量)和Gibbs舍弃量[4]ρva，即

ma=me+ρva

(1)

其中，ρva的物理意义为占据吸附相体积va的空间中具有游离相密度ρ的物质量。通过式(1)的拆分后，将均质的游离相mf和非均质的吸附相ma视为一个整体，可测试出Gibbs吸附量me，具体如下:

me=ma-ρva=(ma+mf)-(mf+ρva)=

(ma+mf)-(ρvf+ρva)=(ma+mf)-ρ(vf+va)=

mtotal-ρvvoid

(2)

其中，mtotal为充入图1所示吸附系统内总的瓦斯量;vvoid为吸附系统内的空隙体积;ρ为游离相浓度，3者全部为可测试的试验变量。换言之，现有的吸附等温线试验方法不可能测试出实际吸附量，只能采用式(1)的原理和式(2)的操作方法测试出Gibbs吸附量。迄今为止，开展气源岩吸附等温线测试的方法有体积法和重量法[4,31-32]，还有我国煤炭行业标准规定的高压容量法(MT/T 752—1997和GB/T 19560—2008)，所有这些方法全部是采用了Gibbs表面过剩吸附模型式(1)的原理，并将图1所示吸附系统内的非均质的吸附相ma和均质的游离相mf视为一个整体，因而将不可测试的实际吸附量转变为Gibbs吸附量按照式(2)进行测试的。从吸附相模型式(1)和吸附试验机理式(2)可以看出以下几点:

(1)低压吸附试验时，图1所示吸附系统内的游离相气体浓度很小ρ→0，且吸附相占有的体积也非常小va→0，式(1)中的ρva可忽略不计，那么式(2)可以简化为me≈ma，即低压吸附时可近似的认为实际吸附量等于Gibbs吸附量，但是迄今为止并没有可忽略ρva的最低压力临界值。

(2)中、高压吸附试验时，ρ和va都很大，ρva不可忽略，从式(2)的数学含义上就能看出:随着吸附压力增大，Gibbs舍弃量[4]ρva增大，Gibbs吸附量me会达到“峰值”并下降。

(3)实验室只能测试出Gibbs吸附等温线，属于“峰值”型吸附等温线，而不可能属于大部分学者得出的Langmuir型吸附等温线。

(4)“峰值”型吸附等温线下降的机理是因为吸附相不可测试而不得不忽略Gibbs舍弃量[4]ρva造成的，并不属于负吸附[20,23-25]、解吸滞后型吸附[16,21]和超临界吸附等[20,22]。

总之，实验室不能测试实际吸附量等温线，只能测试“峰值”型的Gibbs等温线。

1.2 Langmuir模型校正

工程实践中普遍采用Langmuir模型描述实际吸附瓦斯量ma，然而吸附试验机理表明实验室只能测试Gibbs吸附量，因此，为了使Langmuir模型能描述实验室测试的Gibbs吸附等温线，特将Langmuir模型、Langmuir-Freundlich模型[33]和双吸附点Langmuir模型[34]校正为可以描述Gibbs吸附量me的模型。在煤体吸附瓦斯研究中，Langmuir模型常用的形式为

(3)

其中，m0和k0为吸附常数，m0为饱和吸附量或者说饱和吸附能力，k0为与吸附剂、吸附气体的特性和吸附温度有关的系数，是决定吸附性能的关键参数;P为吸附平衡压力。将式(3)代入式(1)可得描述Gibbs吸附量的Langmuir模型:

(4)

部分学者[35-36]在研究煤体吸附CH4和CO2的能力时发现:朗格谬尔公式(3)没有其经验扩展的Langmuir-Freundlich公式拟合煤体吸附等温线实验数据的效果好，Langmuir-Freundlich公式为

(5)

其中，n为吸附剂非均质性的无因次参数。同上，将式(5)代入式(1)可得描述Gibbs吸附量的Langmuir-Freundlich模型:

(6)

此外，部分学者[34,36]认为朗格缪尔假设吸附剂表面性质均一，与自然界的吸附剂表面是非均质的实际情况不符，因此，吸附剂的非均质表面可能具有两种或者两种以上的吸附点。基于这种考虑将均一吸附点的朗格缪尔模型扩展到双重吸附点模型以适应不同的吸附点类型，具体如下:

(7)

其中，k1和k2为两类吸附点各自的朗格缪尔吸附常数;α为每类吸附点的权重(0<α<1)。同上，将式(7)代入式(1)可得描述Gibbs吸附量的Langmuir双吸附点模型:

(8)

2 试验

2.1 煤样制作

本文试验煤样取自河南平煤八矿戊9-10煤层的肥煤，该煤层为煤与瓦斯突出煤层，取样地点附近实测瓦斯含量为2.34～13.99 m3/t，该煤层的肥煤具有吸附量较小的特点，易在较低压力吸附饱和并形成“峰值”型等温线的峰值拐点，而且，构造煤吸附能力普遍大于原生结构煤，特采集了质量约5 kg 左右的构造煤和原生结构煤各一块作为试验对象，并将构造煤样编号为PG1，原生结构煤样编号为PY2。其次，采用行业标准《煤的工业分析方法》GB/T 30732—2014测试了这两份煤样的的物理参数，测试结果见表1。然后，分别将两份煤样破碎后，采用直径为0.25～0.50 mm的煤样筛筛分成煤粒样品。最后，将筛分好的煤粒放入200 ℃的干燥箱去掉水分，然后放入专用煤样瓶以备吸附时使用。

表1 煤样的物理参数

Table 1 Physical parameters of the coal sample

2.2 试验设备与条件

本文采用体积法测试煤样吸附等温线，按照煤炭行业标准“高压容量法”(MT/T 752—1997和GB/T 19560—2008)自制的高压吸附测试装置如图2所示，其测试系统部件主要有煤样罐、参考罐、恒温水浴(精度为±0.1 ℃)、数个耐压30 MPa的截止阀门、量程为0～40 MPa的压力传感器(满程精度为±0.1%)和增压泵等。考虑到Gibbs舍弃量ρva与温度密切相关，温度越高，该量越小，因此，将试验温度设置为10 ℃和30 ℃，既有接近煤层又有相对较低的温度，以便快速达到不可忽视的Gibbs舍弃量ρva，试验压力最高12 MPa，采用纯度达99.99%的甲烷气体进行试验，试验步骤请参见国标GB/T 19560—2008。

图2 煤体瓦斯吸附装置示意

3 试验结果及讨论

3.1 等温线测试结果分析

在10 ℃和30 ℃的恒温条件下，测得构造煤样PG1和原生结构煤样PY2共计4条吸附等温线如图3左侧PG1和PY2原始数据所示，4条等温线均呈现“峰值”型等温线特征，与部分学者[16-18,21]的测试结果基本一致。

图3所示“峰值”型曲线变化特征再次验证了等温吸附试验机理(式(2))测试的是Gibbs吸附量，而不是实际吸附量，其下降原因是Gibbs模型式(1)减去了Gibbs舍弃量ρva造成的，实际吸附瓦斯量并没有下降。根据Gibbs舍弃量ρva的定义，结合本次试验，可以得出“峰值”型等温线出现峰值的临界压力点与以下因素有关:

(1)煤体结构。如图3左侧所示的4条me—P等温曲线，构造煤样PG1的等温线出现“峰值”的临界压力点明显小于原生结构煤样PY2，分析原因是不同的煤体结构决定着Gibbs舍弃量ρva中的吸附相体积va的大小。由表1和图3可以看出，构造煤样PG1与原生结构煤样PY2相比，具有较大的孔隙率、较大的Gibbs峰值吸附量、较快的瓦斯吸附速度[37-38]，因此在较小压力下就在煤基质表面吸附了较大的体积va，从而造就了较大的Gibbs舍弃量ρva。

(2)温压条件。如图3右侧所示煤样PG1-10,PG1-30,PY2-10和PY2-30的4条me—ρ等温曲线，在游离相密度ρ分别为35.45，33.11，49.05和46.93 kg/m3时，其Gibbs吸附量就达到9.40，8.74，10.53和9.63 cm3/g的峰值。可见，同一煤样条件下，游离相密度ρ越大，出现“峰值”的临界压力越小，这是因为不同的温压条件决定着Gibbs舍弃量ρva中的游离相密度ρ的大小。而且，游离相密度ρ是由吸附系统中的温压条件通过气体状态方程计算的，压力相同时，温度越高，游离相密度ρ越小，等温线出现“峰值”的临界压力越大;温度相同时，压力越大，游离相密度ρ越大，等温线出现“峰值”的临界压力越小。

图3 吸附等温线测试结果及截距法示意

综上，“峰值型”吸附等温线出现峰值拐点的本质原因是等温吸附原理中减掉了Gibbs舍弃量ρva，出现“峰值”的临界压力是由两方面因素共同决定的:煤体结构和试验温压条件。

3.2 吸附相密度计算

实际吸附量等温线必须由吸附相密度在Gibbs等温线的基础上进行校正，下面采用截距法[39]、液相替代法[40-41]和Langmuir模型法[42]结合本文试验结果进行吸附相密度计算。

3.2.1截距法

截距法[39]的原理是将式(1)变换成Gibbs吸附量me和游离相密度ρ的线性方程，具体如下:

me=-vaρ+vaρa

(9)

从数学的角度，式(9)中-va为斜率，vaρa为截距，因此，可利用实验室测试的Gibbs吸附等温线的线性下降段求出其下降段的密度。以图3中PG1-30的Gibbs吸附等温线拟合结果为例，其斜率-va为-0.052 5，vaρa为11.708，进一步算出吸附相密度ρa为223.00 kg/m3。截距法[39]的拟合精度如图3右侧部分所示，拟合结果见表2，PG1在10 ℃和30 ℃的吸附相密度分别为238.44和223.00 kg/m3;PY2在10 ℃和30 ℃的吸附相密度分别为214.24和192.86 kg/m3。

表2 吸附相密度计算结果

Table 2 Calculation results of the adsorbed phase density

方法参数煤样PG110℃30℃煤样PY210℃30℃截距法式(9)ρa/(kg·m-3)238.44223.00214.24192.86m0/(cm3·g-1)17.234117.397424.469022.3822式(4)k0/MPa-10.82310.46840.15420.1563ρa/(kg·m-3)172.51151.33172.58163.67m0/(cm3·g-1)21.990117.250326.000025.1274式(6)k0/MPa-10.38830.47640.13650.1296Langmuir模型法ρa/(kg·m-3)165.95152.18171.63154.88m0/(cm3·g-1)18.326717.397225.523830.0000式(8)k1/MPa-10.322570.468410.00000.3492k2/MPa-15.79870.46780.14940.0766ρa/(kg·m-3)169.85151.34175.18146.33沸点液相ρa/(kg·m-3)423液相代替法范德瓦尔体积常数ρa/(kg·m-3)374.82式(10)ρa/(kg·m-3)274.28260.90274.28260.90超临界点ρa/(kg·m-3)162.66

3.2.2液相代替法

液相密度代替法即采用大气压力条件下试验气体沸点的液相密度代替吸附相密度ρa。其中，一部分学者[40]采用的沸点密度分别是:CH4为423 kg/m3;N2为808 kg/m3;CO2为1 180 kg/m3，需要注意的是CO2沸点时为固相。另一部分学者[17,41]认为吸附相密度ρa与沸点密度符合下面的经验公式:

(10)

其中，ρb为沸点密度;Tb为液相温度;T为开展吸附等温线试验时的温度;0.002 5为过热的液相吸附质的热膨胀系数的平均值。

如表2所示，CH4在沸点温度-161.4 ℃时，其液相密度为423 kg/m3。那么，根据吸附相密度ρa与沸点密度的经验公式(10)[41]，结合本文的实验条件，可以求出CH4在10 ℃的吸附相密度ρa为274.28 kg/m3、在30 ℃时吸附相密度ρa为260.90 kg/m3。

3.2.3Langmuir模型法

分别采用式(4)、式(6)和式(8)对图3的4条吸附等温线进行了最优化拟合[40-41]，拟合曲线及对应的残差如图4和5所示，拟合结果见表2，其中，煤样PG1-10为165.95～172.51 kg/m3;煤样PG1-30为151.33～152.18 kg/m3;煤样PY2-10为171.63～175.18 kg/m3;煤样PY2-30为146.33～163.67 kg/m3。

需要强调的是，虽然图4，5显示Langmuir模型法的拟合残差小、精度高，但是该方法运用LM算法[40-41,43]拟合过程中需要人为设定各未知参数的初始值和边界值，这给多参数拟合带来了极大的不确定性，也就是说，不同的人会得出不同的结果，从而造成无可避免的人为误差。

3.3 等温线校正

采用表2中的吸附相密度值将本文测试的4条Gibbs吸附等温线校正成了实际吸附量等温线，其结果如图6所示。

校正后的实际吸附量等温线呈现出3类线性规律:① 第1类是单调上升型，见图6中经验公式和Langmuir模型法的校正结果;② 第2类是先上升后下降型，见图6中液相密度法、范德瓦尔、超临界点的校正结果;③ 第3类是先上升后形成直线平台式的Langmuir型，见图6中截距法的校正结果。这3类较正结果仅第3类是正确的，原因是:

第1，煤、页岩等气源岩吸附属于物理吸附[44]，对于同一条Gibbs吸附等温线，其吸附剂唯一，试验温度恒定，吸附剂表面可供吸附的位置是固定不变的，换句话说，随着压力升高达到饱和吸附时，其饱和吸附量、吸附势等物理量必定是常量，实际吸附量等温线肯定是Langmuir型的，可见，仅截距法是属于这种类型。

图4 Langmuir改进模型对煤样PG1的2条吸附等温线拟合结果

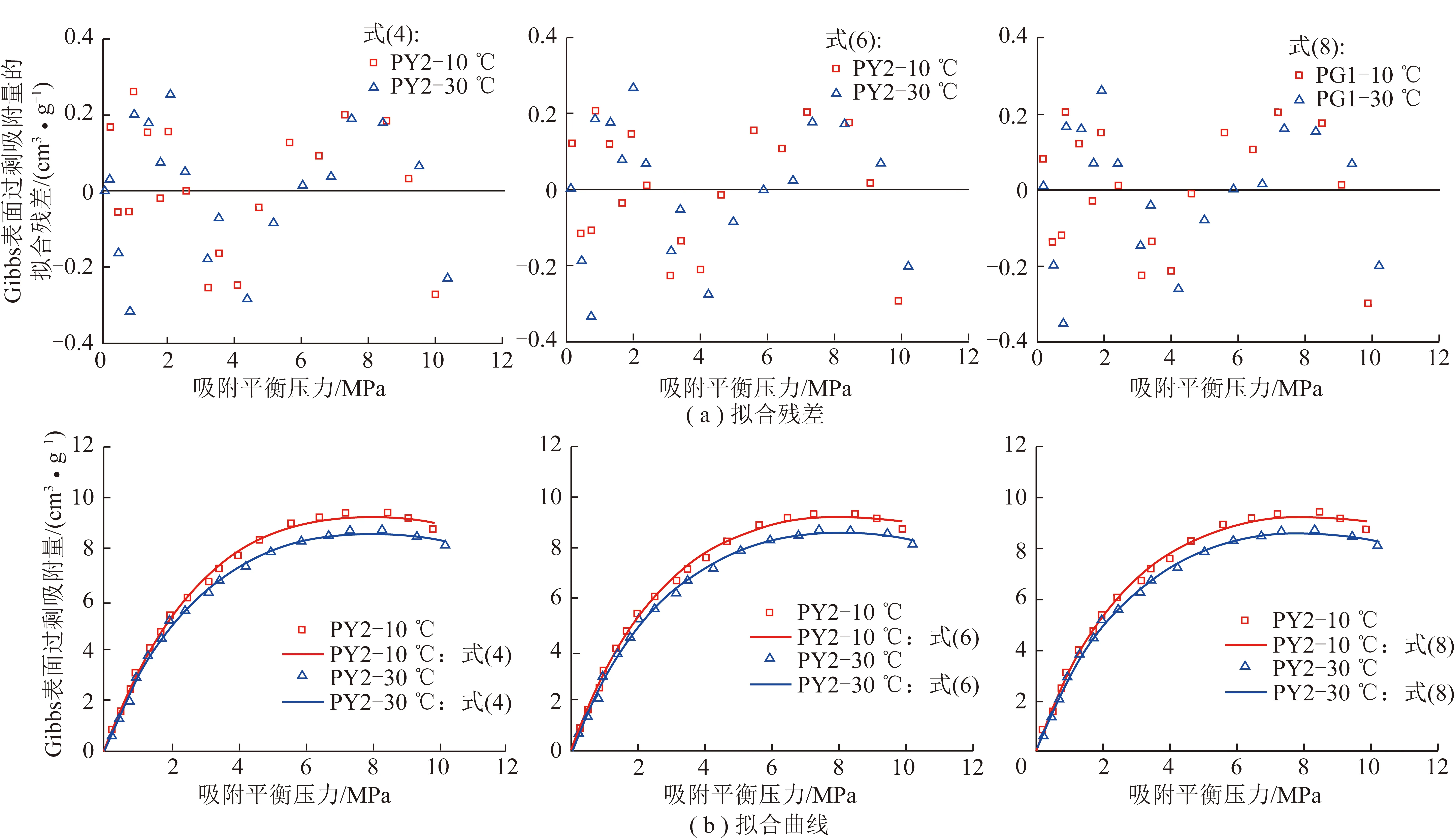
图5 Langmuir改进模型对煤样PY2的2条吸附等温线拟合结果

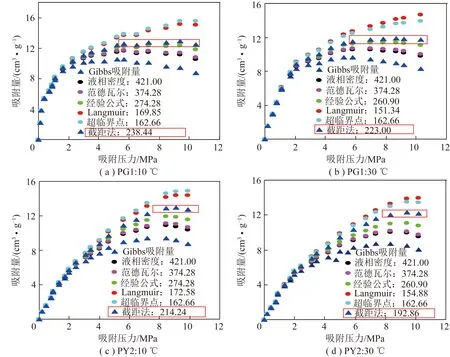
图6 实际吸附量等温线校正结果对比

第2，本文的测试结果(图3)和部分学者的测试结果[19,22,24,45]共同表明“峰值型”等温线的物理特征可分为以下3部分:① 上升部分;② 顶点;③ 线型下降部分，这3部分对应的物理意义[39]为:① 在吸附饱和前，随着吸附压力的增加，游离相密度增大，吸附相密度不断增大，Gibbs吸附量相应的不断增大;② 当吸附压力增大到刚刚吸附饱和时，吸附相密度增大到最大值，此时Gibbs吸附量达到最大值，即达到了Gibbs等温线的峰值顶点;③ 吸附饱和后，实际吸附量饱和并趋于稳定、不再变化，但随着吸附压力的增大，游离相密度继续增大，Gibbs舍弃量ρva不断增大，因此，从等温吸附试验机理公式(2)可以看出，Gibbs吸附量必定线性下降。可见，截距法[39]正是利用了Gibbs吸附等温线线性下降段中实际吸附量趋于饱和这一特定规律进行吸附相密度求解的，因此，其校正的实际吸附量等温线符合物理吸附[44]所形成的Langmuir型等温线，是可靠的。

需要指出的是，国内外部分学者[39,45]也采用截距法对Gibbs吸附等温线进行了校正，一部分[39]认为截距法完全依据试验数据得到的实际吸附量等温线是可靠的;另一部分学者[45]认为Langmuir模型法较截距法可靠，原因是截距法计算的部分吸附相密度值大于大气压力条件下沸点液相密度值423 kg/m3。然而，据SETZMANN和WAGNER的研究[46]，甲烷在临界温度-82.6 ℃以上、压力0.025～1 000 MPa范围内，都是以气体形式存在的，无论怎样也不可以液化，吸附相是吸附力主导的吸附现象，而不是温压主导的凝聚现象，因此，将沸点液相密度值423 kg/m3与吸附相密度进行类比是没有任何理论依据的。而且，本文对Langmuir多参数模型(图4～5)拟合结果后发现:虽然多未知参数拟合的精度很高，但因拟合过程中需人为设定各参数的初始值和调节拟合边界范围[42-43]，造成了很大的人为误差。

综上，截距法完全依靠试验数据所校正出的实际吸附量等温线是可靠的，而Langmuir拟合法存在人为误差、液相密度法仅仅考虑了温压变化对吸附的影响，是不适用的。

4 吸附试验误差及工程风险讨论

4.1 等温吸附试验误差讨论

吸附试验机理公式(2)和吸附试验结果证明:实验室测试的Gibbs等温线只能是“峰值型”等温线，校正后的实际吸附量等温线才是Langmuir型等温线，二者的线性关系特征如图7所示。当前，体积法设备常常测试出[5-6,8]如图7所示饱和前的那部分Gibbs等温线，重量法常常测试出比较精确的“峰值型”Gibbs等温线[17,39-39]，然而，无论是体积法还是重量法的测试结果都不能直接用来计算吸附常数、预测非常规气资源量等，因为直接运用这些测定结果非常容易造成未饱和吸附、未校正或者错误校正、误解试验原理等多方面的误差，具体如下:

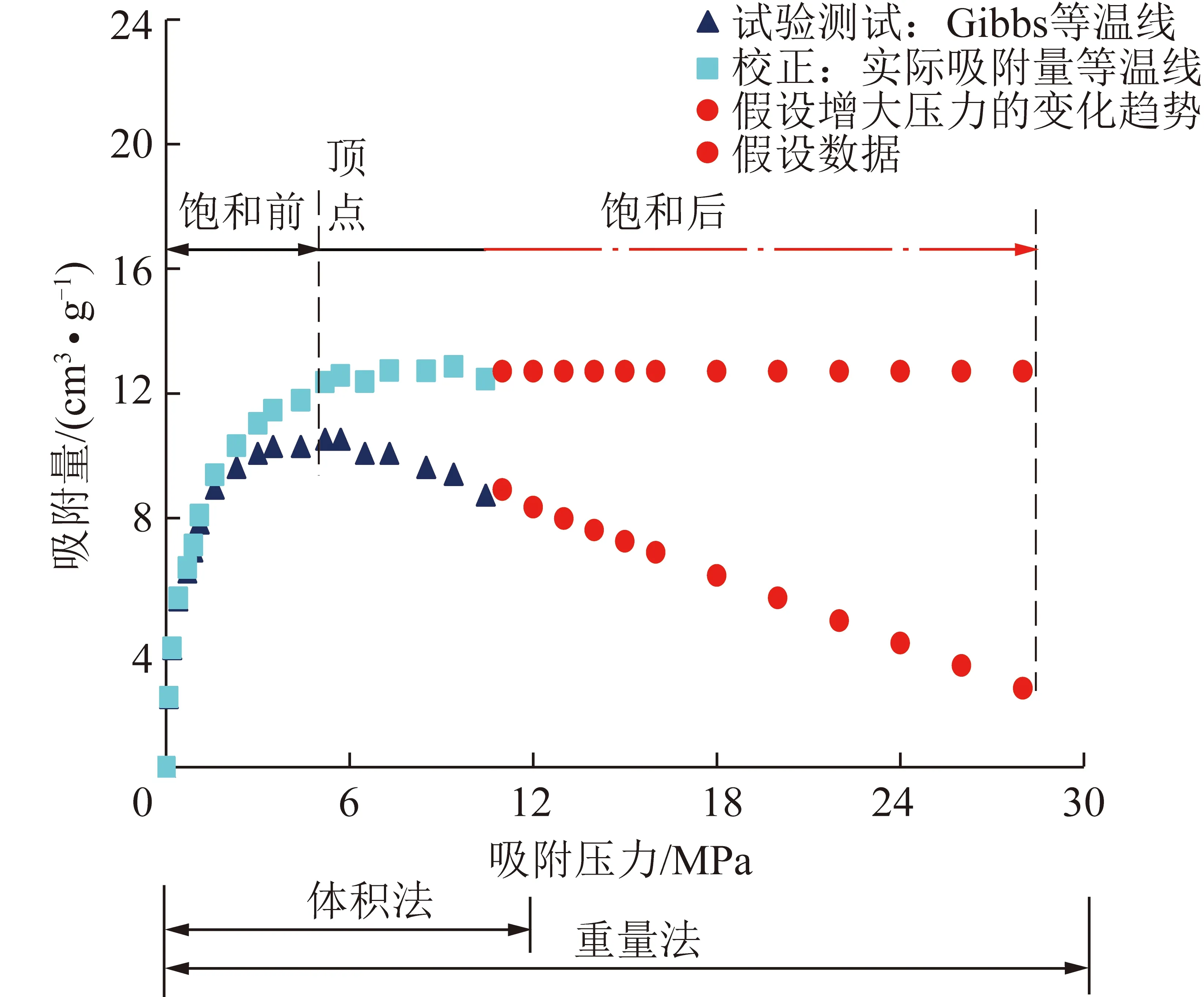
图7 吸附等温线的线性特征(以煤样PG1∶10 ℃为例)

4.1.1未饱和且不校正误差

体积法普遍采用美国Terra Tek公司生产的IS-100-300型吸附仪[7-8,15-17]，试验压力相对较小，一般在0～12 MPa。因此，体积法因其较低的吸附压力常常测试出未饱和吸附的Langmuir型等温线，即如图7所示饱和前的那部分Gibbs等温线，本质原因是该类设备在设计时就假定Gibbs舍弃量ρva是可以忽略的。直接采用[5-6,8]Langumir模型拟合这类未饱和吸附的Gibbs等温线，并进行其所在领域的相关研究，可能存在两方面的误差:① Langumir模型只适用于具有饱和吸附后直线平台式的第Ⅰ类等温线，拟合未饱和吸附等温线所得出的吸附常数肯定有很大误差;② 部分学者[31]认为低压吸附时或者说未饱和吸附时me≈ma(第2.1节)，但是迄今为止并没有明确的可以忽略Gibbs舍弃量ρva的临界压力值。对比本文校正的实际吸附量等温线和Gibbs等温线的未饱和段(图6中蓝色三角形曲线点)可知，二者在很长一段等温线范围内是不相等的，而且，不同煤样不同温度其近似相等的临界压力值也是不一样的，PG1-10,PG1-30分别约为1.9，2.1 MPa;PY2-10,PY2-30分别约为2.3，2.7 MPa。

4.1.2误解吸附试验原理

重量法普遍采用荷兰安米德Rubotherm吸附仪[45]，该类设备可以开展吸附的试验压力相对较大，一般在0～30 MPa，重量法因其较高的吸附压力常常测试出精确的“峰值型”Gibbs等温线，即如图7所示饱和前后整条Gibbs等温线。显然，不能直接采用“峰值型”等温线分析气源岩的真实吸附能力、计算吸附常数或者研究吸附机理，必须进行校正，否则，容易将Gibbs吸附等温线下降现象归因于负吸附、“自由空间体积”变化[23,25]等。

4.1.3校正方法不当

即采用了不适用的吸附相密度值校正Gibbs吸附等温线所得到的实际吸附量等温线。例如，一部分学者[17,40-41]采用沸点液相密度值进行校正，仅仅是将吸附相密度与液相密度进行了简单类比，并没有明确其理论依据;另一部分学者[42,45]采用多参数的Langmuir模型预测密度值进行校正，因多参数迭代需人为给各参数进行初始赋值和范围设定，存在较大的人为误差。

此外，气源岩吸附属于物理吸附，其吸附特征与试验方法的选择无关，如图7所示，体积法常常测试出未饱和的吸附等温线，是因为吸附压力小造成的，如果继续增大其吸附试验压力，必定也能测试出如图7所示重量法所测下降型变化趋势等温线。

4.2 工程实践风险测算

在煤层气、页岩气和矿井瓦斯治理等工程实践中，常采用Langumir模型式(3)拟合实验室测试的吸附等温线得出吸附常数m0，k0值，进而按照该常数进行非常规气资源量反算、瓦斯含量和瓦斯压力互算、饱和吸附量(即吸附常数m0值)预测等。因此，下面以本文测试的4条Gibbs等温线为例，采用Langumir及改进模型拟合这4条等温线的未饱和段、饱和曲线得出了吸附常数m0(饱和吸附量)、k0值，并以截距法校正的实际吸附量等温线的饱和吸附量m0为参考标准，对比了等温线误差所带来的潜在工程实践风险，对比结果见表3。

表3 常见Gibbs等温线误差带来的工程风险对比

Table 3 A complete comparison on engineering risk caused by Gibbs isotherm errors

煤样及温度未饱和吸附(式(3))m0/(cm3·g-1)k0/MPa-1饱和吸附(式(4))m0/(cm3·g-1)k0/MPa-1截距法m0/(cm3·g-1)未饱和吸附∗绝对误差相对误差/%饱和吸附∗绝对误差相对误差/%PG1-10℃11.542.0217.23410.823112.621.088.56-4.61-36.56PG1-30℃12.450.7517.23410.468411.77-0.68-5.78-5.63-47.81PY2-10℃13.810.3124.46900.154212.85-0.96-7.47-11.62-90.42PY2-30℃12.610.3222.38220.156312.18-0.43-3.53-10.20-83.76

注：*以截距法作为参考标准。

由表3可知，采用Langumir模型式(3)拟合未饱和吸附的Gibbs等温线造成的饱和吸附量相对误差为-3.53%～8.56%，而且，煤样PG1出现了温度较高饱和吸附量反而较大的常识性错误;采用Langumir改进的三参数模型式(4)拟合饱和吸附的Gibbs等温线造成的饱和吸附量相对误差为-90.42%～-36.56%。