考虑水分影响的煤岩渗透率模型及演化规律

2019-12-16李波波李建华任崇鸿

煤炭学报 2019年11期

李波波，李建华，杨康，任崇鸿，许江，高政

(1.贵州大学矿业学院,贵州贵阳 550025; 2.贵州大学喀斯特山区优势矿产资源高效利用国家地方联合工程实验室,贵州贵阳 550025; 3.山东科技大学矿山灾害预防控制省部共建国家重点实验室培育基地,山东青岛 266590; 4.重庆大学煤矿灾害动力学与控制国家重点实验室,重庆 400044)

在煤层气开采过程中，提高煤层瓦斯存储量的预测精度是煤层气生产的关键，同时瓦斯排放也是限制煤矿生产的重要问题之一[1]。煤层中的水分主要为自由水和结合水，渗透率通常与水分含量的变化有关[2]。在自由水流动过程中，煤岩孔裂隙表面会形成厚度不均的水膜，对吸附性多孔介质的气体渗透特性具有重要影响[3]。因此，研究动态水膜厚度变化对煤层瓦斯的运移具有重要意义，并且也为瓦斯灾害防治提供借鉴。

储层条件下的煤岩渗透率演化机理十分复杂，受到有效应力、滑脱效应和水分等因素的制约。唐巨鹏等[4]发现在气体压力加载过程中，吸附作用会导致渗透率的变化。肖晓春等[5]得到滑脱效应可增大低渗多孔介质渗透率。李立功等[6]得到克林伯格系数与渗透率呈指数关系。同时，在自然界煤岩中的水分是影响煤中瓦斯气体赋存、扩散、渗透率和煤岩孔裂隙变形的主要因素[7]。魏建平等[8]得到型煤的渗透率与水分及围压呈现负相关的关系。袁曦等[9]通过试验研究得到，水分对瓦斯压力敏感性随着含水率的增大而增大，煤渗透率与含水率呈线性减小的关系。水分对瓦斯的吸附作用的影响可通过试验和理论模型量化[10]。JOUBERT等[11]和LEVY等[12]基于水分含量与气体吸附量的关系式，提出“水分效应系数”并验证了关系式的合理性。SHI等[13]得到水分含量对煤岩吸附能力的影响存在临界值。在渗流过程中，介质内薄膜(水膜)与孔壁之间的相互作用也不容忽视[14]。TENG等[15]认为水膜厚度的减小会使煤层渗透率增大。为量化水分对煤岩渗透率的影响，MIAO等[16]通过试验验证相对湿度对煤岩渗透特性的影响，并构建考虑水分及其物性质的渗透率模型。

综上所述，对于不同含水条件下的煤岩吸附及渗流的试验和模型，分析中往往很容易低估水膜厚度及稳定性对煤岩渗透特性的影响。笔者在此前已经进行了相关的试验研究和分析，并构建了考虑含水率的煤岩吸附及渗透率模型[17]，但尚未考虑真实现场抽采条件，煤岩含水状态的瓦斯运移规律，也未考虑动态的水膜厚度对煤岩的吸附及渗透率变化影响。为准确的表征煤岩吸附和渗流特性，笔者在此基础上，考虑瓦斯-水环境中的吸附特性，改进吸附变形模型。综合考虑表面相互作用力的影响和简化的水膜厚度方程，进一步构建考虑水膜影响的渗透率模型，通过试验验证其合理性，同时考虑压缩变形对渗透率的贡献。为下一步煤岩吸附水和瓦斯变形-渗透率模型构建奠定理论基础，将对含水煤岩的瓦斯抽采和瓦斯灾害的防治产生积极影响。

1 考虑水分影响的煤岩渗透率模型

1.1 煤岩表面的水膜厚度h

储层条件下，在煤岩孔裂隙中自由水易产生不连续水膜会直接占据渗流通道。其中，分离压与环境相对湿度的关系[2]可以表示为

(1)

式中，pv/p*为饱和蒸气压，无量纲;R为理想气体常数，J/(mol·K);T为温度，K;RH为环境相对湿度，%;Π(h)为水膜-孔壁微观作用力(Π(h)=Π1(h)+Π2(h)+Π3(h))，并且

(2)

将式(2)代入式(1)化简，得到水膜厚度h为

(3)

式中，n为含水饱和度，%。

1.2 考虑水分影响的煤岩吸附模型

试验中过剩吸附量[18]通常表示为

(4)

式中，Vex和Vabs分别为过剩吸附量和绝对吸附量，cm3/g;ρg和ρads分别为气体密度和吸附相密度，g/cm3，将吸附相密度取定值0.423 g/cm3[17]。

通常不同含水条件下的吸附量(其中吸附及渗流特征如图1所示)可表示[10]为

(5)

式中，Vs为单位质量煤体的气体吸附量，cm3/g;VL为Langmuir吸附体积常数，cm3/g;pL为Langmuir吸附压力常数，MPa;p为孔隙压力，MPa;α为湿度对煤体吸附能力的衰减系数;m为含水率。

通过式(4)～(5)，经计算化简可得考虑水分影响的吸附模型可表示为

(6)

图1 煤岩不同含水条件下的吸附和渗流示意

1.3 外应力恒定时的基质及裂隙宽度变化

1.3.1基质宽度的变化

假设煤岩各向同性，则有效应力影响的煤基质尺寸变化量[19]为

(7)

式中，Δae为有效应力作用下的煤基质宽度变化量，m;εme为有效应力作用下的体积应变;a0为煤基质初始尺寸，m;Km为煤基质的体积模量，MPa;σ为平均应力，MPa;S为应力系数，取值1。

在吸附过程中，煤岩表面自由能可表示[20]为

(8)

式中，π为表面自由能，J;Γ为表面超量，有

(9)

式中，A为比表面积，cm2;V0标准气体摩尔体积，22.4 L/mol。

煤岩产生的变形可用相对线性变化表示:

(10)

式中，Δl/l为相对线性变形;γ为变形常数(γ=Aρc/EA);EA为吸附模量，30 ℃时取178.88 MPa[17];ρc为煤岩密度，试验测得1.6 g/cm3;p0为初始孔隙压力，MPa。

考虑三轴应力的边界条件，将式(10)进行计算化简，得到考虑水分影响的吸附变形模型为

(11)

式中，Δεs为考虑水分影响的吸附变形。

吸附作用通常会改变煤基质尺寸，这种变化[21]可用方程表示为

(12)

1.3.2裂隙宽度的变化

作为多孔介质，裂隙同样也会受到有效应力的影响。因而，应力影响的裂隙宽度变化量[21]为

(13)

式中，Kf为裂隙体积模量，MPa;εbe为有效应力影响下的裂隙应变;β为常数，计算值为1。

在孔隙压力作用下，裂隙会发生不同程度变化。可将孔隙压力影响的裂隙宽度变化[21]表示为

(14)

由于煤岩的裂隙网络分布复杂，通常将考虑吸附作用影响的裂隙宽度可表示为

(15)

式中，f为吸附应变系数，取值范围为0～1。

1.4 改进的渗透率模型

在应力影响下，煤岩通常发生压缩变形，将Cf定义为裂隙压缩系数(MPa-1)，表示裂隙体积的相对变化，且Cf=1/Kf。将Cm定义为基质压缩系数(MPa-1)，表示基质体积的相对变化，且Cm=1/Km[22]。

裂隙压缩系数与基质压缩系数[23]的关系为

(16)

式中，φ0为初始孔隙率(试验测得0.042)，可通过几何关系[21](图2)得到:φ0=3b0/a0。

图2 火柴棍模型

同时，煤岩孔隙率的定义[24]为

(17)

式中，Vp为孔隙体积，cm3;Vb为基质体积，cm3。

其中，孔隙率的变化率可通过方程表示为

(18)

其中，εb为基质变形量;εp为孔裂隙变形量。式(18)经过计算化简可得

(19)

式中，εp0和εb0分别为初始基质和裂隙变形量。

孔裂隙体积变形量和基质变形量可为

(20)

式中，b为裂隙宽度(b=b0+Δbt)，m;a为基质尺寸(a=a0+Δat)，m。

整理式(3)，(13)～(15)可得裂隙总变化量为

(21)

同理，整理式(7)和式(12)可得基质总变化量为

(22)

将式(20)～(23)代入式(19)中，并经过计算化简可得改进的孔隙率方程为

(23)

式中，Δp为孔隙压力的变化量，MPa。

基于立方定律[24]，可得渗透率与孔隙率比值为

(24)

式中，k0为初始渗透率，10-15m2。

在孔隙压力较低时，滑脱效应对渗透率具有一定的贡献作用[25]，考虑滑脱效应影响的渗透率为

k=ka(1+B/p)

(25)

式中，ka绝对渗透率，10-15m2;B为滑脱因子。

考虑应力、水分及滑脱效应的综合作用，建立考虑水分影响的煤岩渗透率模型可表示为

(26)

2 试验方法

2.1 试样制备

试验样品取自松藻煤矿K2煤层，样品采集完毕后，利用粉碎机将原煤粉碎，筛成60～80目的煤粉颗粒，向煤粉中加入适量蒸馏水，并搅拌均匀并采用刚性试验机在模具中将煤粉压制成φ50 mm×100 mm标准试件。取制作好的型煤煤样烘干，得到干重为wd。之后将干燥煤样在密闭容器中浸泡，并抽真空得含水煤样，称量煤样的质量wm。最终，煤样的含水率为

(27)

重复上述操作即可获得不同含水率煤样。

2.2 试验方案

试验分为:① 利用等温吸附装置进行吸附试验;② 利用自主研发的含瓦斯煤热-流-固耦合三轴伺服渗流装置[26]进行渗流试验，试验系统如图3所示。将纯度为99.99%的CH4作为试验气体，并分别进行不同含水条件下的煤岩吸附试验和孔隙压力升高的渗流试验(具体试验步骤见文献[17])。

图3 渗流试验系统

3 模型验证及试验结果分析

3.1 水分对煤岩吸附特性的影响

将试验数据代入式(6)和式(11)中，得到不同含水率煤岩吸附量与孔隙压力的关系(图4(a))及吸附变形与孔隙压力的关系(图4(b))。由图4可知:

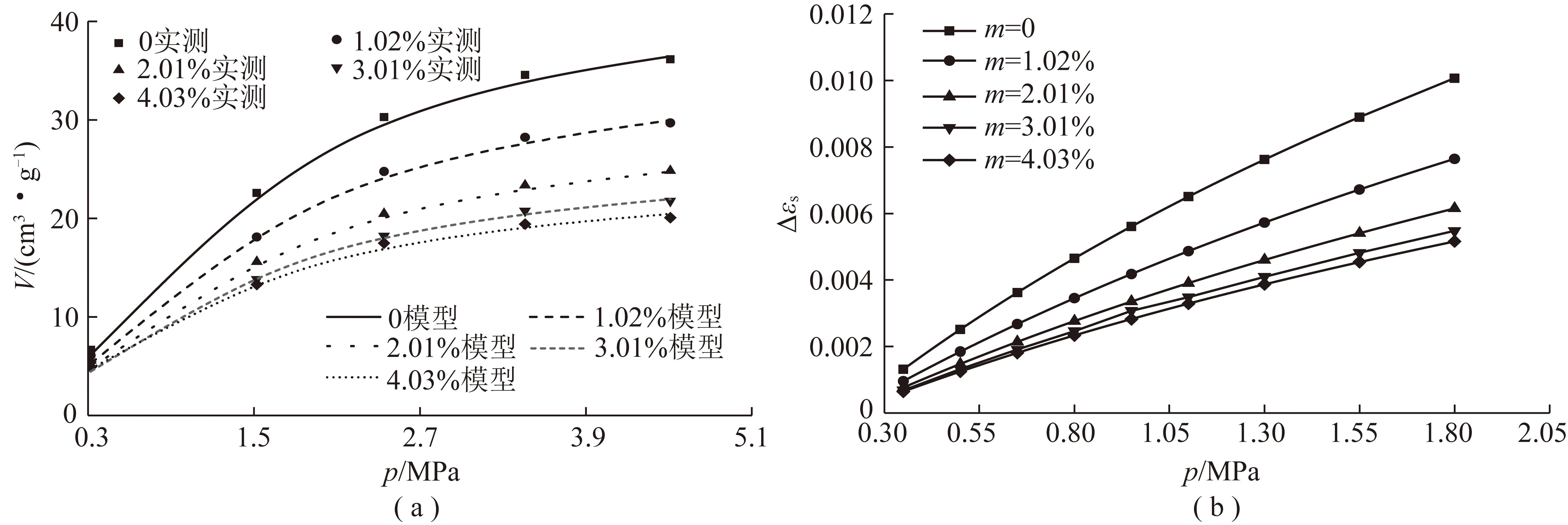
图4 不同含水条件下吸附量、吸附变形与孔隙压力的关系

(1)吸附量实测值与模型计算值基本吻合，表明式(6)可较好的描述水分对含水煤岩瓦斯吸附量的影响规律。随孔隙压力增大，吸附量先增大后趋于平缓，并且吸附量随含水率增大而减小。这是由于吸附作用随孔隙压力增大而增强，对应瓦斯吸附量增大。煤岩的吸附量渐达到饱和时，孔隙压力对吸附作用的影响减弱[4]，吸附量渐趋于恒定。由于亲水基团影响，煤岩吸附位数量逐渐减少[8]。此外，吸附量也受到煤岩水膜和毛细凝聚作用影响[27]。

(2)在水分和孔隙压力的综合作用下，吸附变形随孔隙压力增大而增大，并且随含水率增大而减小。究其原因，煤岩吸附瓦斯产生变形，孔隙压力越大则产生变形量越大。水分通常会弱化煤岩的吸附作用，使吸附量减少，进而导致吸附变形量减小。

3.2 渗透率模型验证及演化规律

通过计算式(26)得到不同含水条件下的煤岩渗透率，图5为煤岩渗透率与孔隙压力的变化关系。

图5 不同含水条件下渗透率与孔隙压力的关系

由图5可知，渗透率模型计算值与试验数据基本吻合，可较好的描述含水煤岩的渗透率演化规律。当含水率恒定时，煤岩渗透率随孔隙压力增大呈先减小后趋于平缓的趋势。孔隙压力恒定时，随含水率的增大，渗透率逐渐减小。究其原因，在孔隙压力增大前期，由于孔隙压力增大导致有效应力减小，造成煤孔裂隙闭合，同时也导致瓦斯渗流通道减小。而瓦斯吸附层和煤基质吸附变形量也会阻碍了孔裂隙中的瓦斯流动，进一步导致渗透率降低。在这个过程中，吸附作用主导渗透率的变化[4]。同时在孔隙压力较低时，滑脱效应对煤岩渗透率也有一定的影响。但是在孔隙压力增大过程中，滑脱效应逐渐减弱，煤岩的瓦斯吸附量渐趋于饱和，产生的膨胀变形量趋于稳定，导致渗透率变化渐趋于平缓。同时，水分也影响渗流通道，导致煤岩渗透率随含水率增大显著减小。此外，不同水分导致压缩系数和滑脱因子等参数值也不相同(表1)。

表1 渗透率模型参数

Table 1 Permeability model parameters

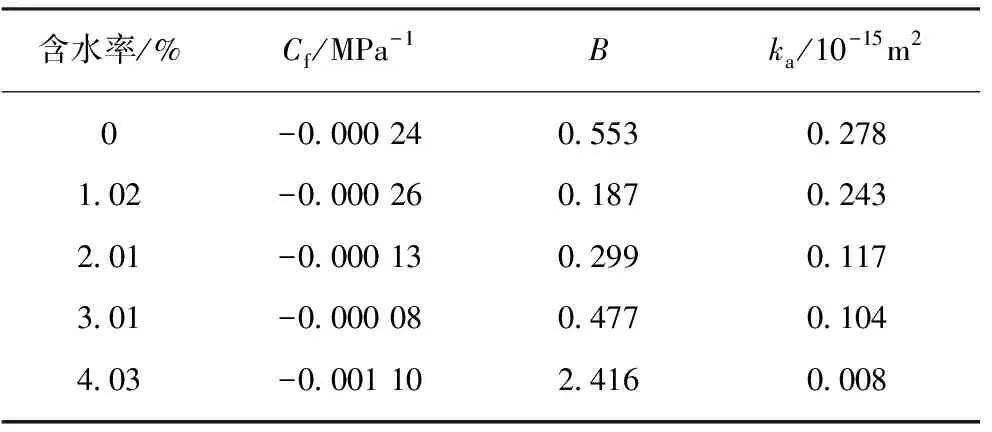
含水率/%Cf/MPa-1Bka/10-15m20-0.000240.5530.2781.02-0.000260.1870.2432.01-0.000130.2990.1173.01-0.000080.4770.1044.03-0.001102.4160.008

3.3 水分对瓦斯流动性的影响

图6为瓦斯流量与含水率关系。由图6可知，随含水率增大，瓦斯流量逐渐减小，而且瓦斯流量随孔隙压力增大而减小。究其原因，水分子具有极性，在与甲烷的竞争吸附过程中，煤岩将优先吸附甲烷[8]。在水分流动过程中易在孔壁形成水膜，而且水膜随含水率增大而变厚，渗流通道也逐渐减小。在较小孔隙中则产生毛细凝聚作用，导致渗流通道阻塞[27]。此外，水分还会改变瓦斯渗流过程中的黏滞阻力。因此，瓦斯流量总是随含水率增大而减小。而吸附作用随孔隙压力增大而增强，故瓦斯流量又随孔隙压力升高而减小。